基于快速自适应非局部均值滤波的地震随机噪声压制方法

崔亚彤，王胜侯，蔡忠贤

(1.天津市勘察设计院集团有限公司，天津 300191；2.中国地质大学(武汉) 资源学院，湖北 武汉 430074)

0 引言

噪声压制在地震数据处理中起着至关重要的作用，去噪效果将直接影响地震资料解释工作。为了有效压制地震资料随机噪声，提高地震资料的信噪比，国内外许多学者提出了不同的方法，本文将这些方法大致分为5类。首先是基于数学变换的方法，如Fourier变换[1]、Radon变换[2-3]、Curvelet变换[4-6]、Dreamlet变换[7]和Wavelet变换[8-9]；第二种是基于预测滤波的方法，如F-X预测滤波[10-11]和自适应预测方法[12]；第三种是基于非局部均值(NLM)滤波的方法，如传统NLM方法[13-14]和自适应NLM滤波[15-16]；第四种是基于降秩的方法，如矩阵降秩法[17-19]和张量降秩法[20-21]；第五种是基于人工智能的方法，如数据驱动紧密框架[22]和机器学习[23-27]。

与预测滤波方法和降秩滤波方法不同的是，NLM方法并不基于线性假设，因此在处理弯曲同相轴时，该方法可以有效地保护有效信号，压制随机噪声。传统NLM方法起源于图像的随机噪声压制处理[28]，随后Bonar成功地将该方法引入到地震数据噪声压制处理中[13]。然而，传统NLM方法在应用上也存在一定局限性。相比于矩阵降秩或预测滤波等方法，该方法计算时间较长，在处理大型地震数据时效率低下。为了解决这一问题，前人提出了分块NLM法[28]、并行分块NLM法[29]、基于随机投影算法的NLM法[30]、下采样的快速NLM法[31]、变窗口的快速NLM法[32]等。但由于前述方法为了提高计算效率，在计算过程中并没有完全遍历每个数据点，因此可能会牺牲计算精度。而基于数据积分算法的快速NLM法[33]，原理上等价于在计算过程中遍历所有数据点，因此在提高计算速度的同时避免了牺牲精度的可能。传统NLM方法在处理实际地震数据时，所选择的滤波参数值通常为一常数，为了进一步提高去噪效果，前人利用结构张量算法[34-35]、矩阵本征特性算法[36]、灰色关联分析算法[37]等方法，针对不同区域可选择不同的滤波参数来提高去噪效果，但会明显增加计算量。NLM方法的去噪效果很大程度上受滤波器参数的选择影响，如果参数太大，就会丢失细节信息，使图像模糊，如果参数过小，则噪声不能被完全抑制。因此，一些学者通过局部数据的随机噪声估计来自适应的计算滤波参数，例如高通滤波法[38]和最小方差估计法[15-16]。上述这些方法在提高传统NLM方法去噪效果的同时，可以减少滤波参数对计算速度的影响，但该方法在计算效率上仍有提升空间。

本文提出了一种基于快速自适应非局部均值滤波的地震随机噪声压制方法，可快速且有效地压制地震随机噪声。首先，为了提高NLM方法的计算效率，本文给出了一种中心对称数据积分算法，有效地降低了计算成本。其次，通过计算两个邻域窗口的相似度，本文给出了利用均匀度来自适应调整滤波参数分布的方法。最后，通过模型数据和实际数据验证了该方法的有效性、实用性。

1 方法

1.1 非局部均值滤波方法

噪声数据Dnoise(t,x)可由下式表示：

Dnoise(t,x)=Dtrue(t,x)+n

(1)

式中：Dtrue(t,x)表示无噪声数据；n表示随机噪声。假设(Ds,Ds)表示搜索窗口半径，(ds,ds)表示邻域窗口半径，Ddenoise(t,x)表示去噪后的数据，通过对Dtrue(t,x)进行加权平均计算即可得到每个点处的Ddenoise(t,x)数据[13, 28]。因此，Ddenoise(t,x)可以表示为：

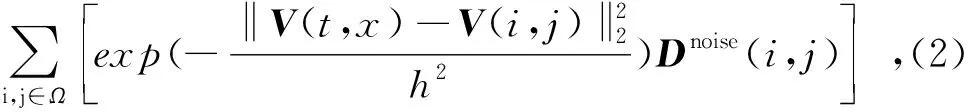
(3)

Ω={i,j∈Ω:|i-t|≤Ds,|j-x|≤Ds}。

(4)

NLM方法可以有效地处理弯曲同相轴，但计算成本较高。假设Dnoise(t,x)总点数为N=NtNx，两个正方形邻域窗口之间的相似度计算量为d2=(2ds+1)2。对于Dnoise(t,x)中的每个数据点，必须在搜索窗内计算D2=(2Ds+1)2次相似度，NLM滤波的计算复杂度为O(ND2d2)，计算量巨大。因此，传统NLM方法在处理大型实际地震数据时，会明显受到计算效率的制约。

1.2 中心对称数据积分算法

={r1,r2∈；|r1|≤Ds,|r2|≤Ds} ，

(5)

={t,x∈;1≤t≤t1,1≤x≤x1} ，

(6)

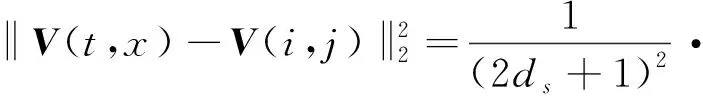
[St(t+ds,x+ds)+St(t-ds-1,x-ds-1)-

St(t+ds,x-ds-1)-St(t-ds-1,x+ds)]，

(7)

通过观察式(5)，发现建立的差分矩阵s(t,x)为中心对称的，因此本文给出了一种中心对称数据积分算法，利用数据积分的数学对称性来提高NLM方法的计算效率。假设

进一步的，上式可推导为:

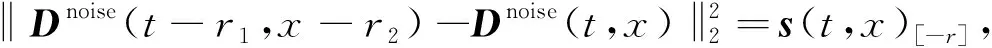
(9)

据此s(t,x)[-r]的值可被表示为s(t,x)[+r]的中心对称值，在计算过程中，即可避免构建s(t,x)[-r]矩阵，进而减少了一半的计算量，将式(9)代入式(6)中，

St(t1-r1,x1-r2)[+r]=St(t1,x1)[-r]，

(10)

再将式(10)代入式(7)中，得到：

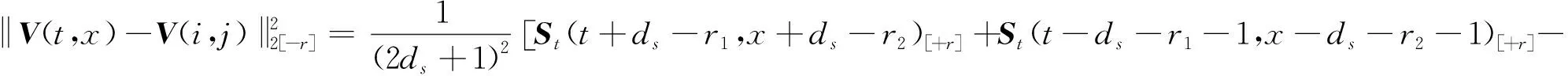
St(t+ds-r1,x-ds-r2-1)[+r]-St(t-ds-r1-1,x+ds-r2)[+r]]。

(11)

1.3 均匀性估计

式(2)中的滤波参数h的选择，对于NLM方法的去噪效果是至关重要的。大量地震资料表明，不同地层的有效信号能量差异较大，甚至随机噪声的分布也不是完全随机的，因此滤波参数h的取值通常难以确定。相比于整个区域的地震数据取相同的滤波参数h， 利用一个参数矩阵h来控制不同区域数据的去噪水平可以提高噪声压制效果。基于最小方差估计的自适应算法可以自适应选择滤波参数h[15-16]，该方法认为参数h的估计是噪声σ的标准差，满足下式

2σ2，

(12)

其中，V0代表无噪声数据。自适应滤波参数矩阵h2的估计即可表示为

(13)

通过利用最小方差估计的方法即可调整整个数据区域内部的滤波参数值。图1给出了一个含噪声数据估计的滤波参数h2的分布情况，如图1c所示，利用最小方差估计方法得到的滤波参数h2在有效信号结构边缘处相对较大，而背景均匀区域的滤波参数值相对较小。

a—无噪声的数据；b—加噪数据；c—最小方差估计的参数分布情况；d—相似度标准差的参数分布情况a—noise-free data;b—noisy data;c—parameter distribution of minimum variance estimation;d—parameter distribution of standard deviation of similarity图1 滤波参数h2分布Fig.1 Distribution of the filtering parameter h2

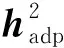
(14)

式中，STDs(t,x)代表相似度的均方差，

Ω={i,j∈Ω；|i-t|≤Ds,|j-x|≤Ds} 。

(15)

本文给出的基于快速自适应非局部均值滤波方法，通过引入中心对称数据积分算法进一步提高了传统NLM方法的计算效率，同时利用相似度标准差来估计均匀性，实现了自适应滤波参数调整，有效地提高了去噪效果和计算效率。

2 模型数据试验

在地震数据噪声压制处理中，通常采用信噪比(SNR)[40]、峰值信噪比(PSNR)和均方误差(MSE)[41]来定量分析方法的地震数据去噪效果，其定义如下:

(16)

(17)

(18)

式中：Dtrue和Ddenoise分别代表原始无噪声数据和噪声压制后数据；N=NtNx表示噪声数据Dnoise(t,x)的总点数。结合传统NLM方法[13]和基于最小方差估计的NLM方法[15]与本文快速自适应NLM方法进行对比，利用2个模型地震数据，从计算效率和精度两方面分别验证本文方法的有效性。

模型数据试验1为简单合成地震剖面，包括两个线性同相轴和两个弯曲同相轴。图2a为60道无噪声模型数据，图2b为加噪数据，信噪比为-4.55 dB，图2c～h分别为传统NLM法、基于最小方差估计的NLM法和本文方法的去噪结果及相应的残差剖面。由于F-X预测滤波方法[10]和降秩方法[18]算法本身基于线性假设，因此对于弯曲同相轴的处理存在误差，而NLM方法对于弯曲同相轴的计算精度就要明显高于上述两种方法(图2c～h)。由于从图中很难看出3种NLM方法的不同之处，因此分别计算上述方法去噪结果的SNR、PSNR和MSE，如表1。可以看出，利用本文方法得到的SNR和PSNR都高于其他方法，且MSE明显低于其他方法，该方法对于随机噪声的压制效果要优于上述其他方法。

a—无噪声的数据；b—噪声数据(SNR=-4.55 dB)；c—传统NLM方法去噪结果；d—a与c的差剖面；e—基于最小方差估计的NLM方法去噪结果；f—a与e的差剖面；g—本文方法去噪的结果；h—a与g的差剖面a—noise-free data;b—noisy data(SNR=-4.55 dB);c—denoised result by using conventional NLM method;d—difference between a and c;e—denoised result by using NLM based on minimum variance estimation;f—difference between a and e;g—denoised result by using proposed method;h—difference between a and g图2 模型试验1的合成模型数据噪声压制结果Fig.2 Noise attenuation results of synthetic model data from model data test 1

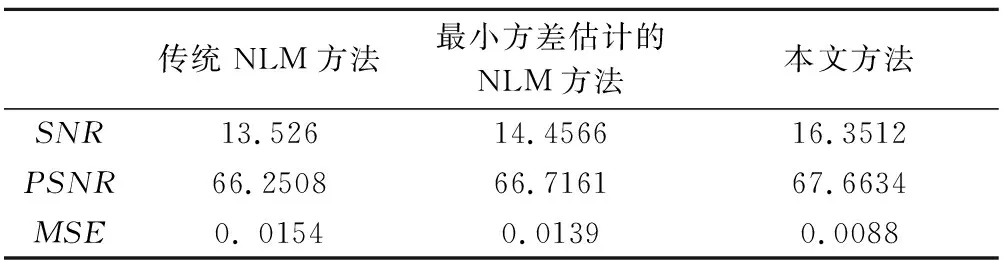
表1 不同方法的SNR、PSNR和MSE对比Table 1 Comparison of SNR,PSNR and MSE using different methods

模型数据试验2为正演偏移剖面。图3a为100道无噪声模型数据，图3b为噪声数据，其信噪比为-3.01 dB，图3c～h分别展示了传统NLM方法、基于最小方差估计的NLM方法和本文方法去噪后的结果及相应的残差剖面。上述方法去噪后的SNR分别为17.254 5 dB、20.727 4 dB、22.557 9 dB，利用本文方法去噪结果的SNR最高。结果表明，本文方法除在合成数据的残差剖面中泄漏少量能量外，在压制随机噪声和保留有效信号方面具有较好的效果。

a—无噪声的数据；b—噪声数据(SNR=-3.01 dB)；c—传统NLM方法去噪结果；d—a与c的差剖面；e—基于最小方差估计的NLM方法去噪结果；f—a与e的差剖面；g—本文方法去噪的结果；h—a与g的差剖面a—noise-free data;b—noisy data (SNR=-3.01 dB);c—denoised result by using conventional NLM method;d—difference between a and c;e—denoised result by using NLM based on minimum variance estimation;f—difference between a and e;g—denoised result by using proposed method;h—difference between a and g图3 模型试验2的合成模型数据噪声压制结果Fig.3 Noise attenuation results of synthetic model data from model data test 2

最后，利用一系列不同大小的地震数据对比不同方法的计算时间。图4a显示了本文快速自适应NLM方法、基于数据积分方法的NLM方法、基于最小方差估计的分块NLM方法和传统NLM方法的计算时间对比。图4b显示了不同信噪比的噪声地震模型数据下，这些方法的去噪质量。与其他方法相比，本文方法计算效率明显高于其他方法，且当利用不同信噪比的模型进行去噪处理后，本文方法也具有更好的去噪质量。

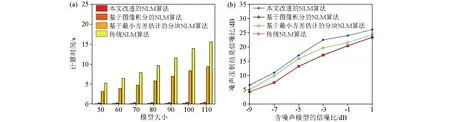
a—计算时间对比；b—去噪质量对比a—computational time comparison;b—denoising quality comparison图4 基于模型数据2不同方法去噪计算时间及效果对比Fig.4 Comparison of calculation time and effect of different denoising methods based on model data test 2

3 实际数据试验

为了验证本文快速自适应非局部均值滤波方法的实用性，将该方法应用于实际地震数据的随机噪声压制处理中，结果如图5所示。从图5a中方框区域可以看出，随机噪声污染了实际地震资料，使得地层模糊，断层构造不清晰，难以进行后续地震资料解释工作。图5b～d分别展示了传统NLM方法、基于最小方差估计的NLM方法以及本文方法的去噪结果。图5e～g显示了这些方法的差剖面。从图5b～g可以看出，传统的NLM方法、基于最小方差估计的NLM方法以及本文提出的方法都可以有效压制随机噪声。但从图5b、5c和5d中的方框区域可以看出，本文方法处理结果中的断层结构相比于另外两种方法更加清晰，有效信号的信息得到了很好的保存，有效地压制了随机噪声。在实际地震数据的噪声压制处理中，本文快速自适应NLM方法、基于数据积分方法的NLM方法、基于最小方差估计的分块NLM方法和传统NLM方法的计算时间分别为：0.63 s、1.14 s、58.42 s和94.22 s。本文提出方法的计算时间也有明显的提高。因此，在处理大型地震数据资料时，本文快速自适应非局部均值滤波方法具有更好的实用性。

a—实际地震数据;b—传统NLM方法去噪结果;c—基于最小方差估计的NLM去噪结果;d—本文方法去噪结果;e—a与b的差剖面;f—a与c的差剖面;g—a与e的差剖面a—field data;b—denoised result by using conventional NLM method;c—denoised result by using NLM based on minimum variance estimation;d—denoised result by using proposed method;e—difference between a and b;f—difference between a and c;g—difference between a and e图5 实际地震数据去噪结果Fig.5 Noise attenuation results of field data

4 结论

本文给出了一种用于地震资料随机噪声压制的快速自适应非局部均值滤波方法。首先，基于数据积分算法的数学对称性，利用中心对称数据积分算法来加速传统NLM滤波方法。其次，利用相似度标准差来估计均匀性，自适应地计算NLM滤波参数，进一步提高噪声压制效果。因此，本文方法在有效提高计算效率的同时，又提高了噪声压制的效果。最后，通过对模型数据和实际数据的处理，验证了该方法的有效性、实用性。