一种用于新能源承载力分析的改进粒子群算法*

2022-10-28储国良邵竹星孙文兵任泰安

西安工业大学学报 2022年5期

储国良，邵竹星，孙文兵，任泰安，吴磊

(1.国网安徽省电力有限公司安庆供电公司，安庆 246003；2.合肥工业大学本科生院工程素质教育中心，合肥 230009)

近年来，由于能源和环境问题的日益严峻，新能源发电正在受到越来越多的关注。新能源大量接入电网，会对电网的稳定运行造成影响[1-2]，因此有必要进行电网新能源承载能力的研究，确定电网能够接入的最大新能源容量，找出限制新能源接入的限制因素，从而为电网规划提供参考。

目前有关新能源承载能力方面的研究，均需要建立电网新能源承载能力分析的数学模型，并提出相应的求解方法，如典型日法[3-5]、时序仿真法[6-7]、迭代寻优算法[8-9]等，这些方法都能够有效地评估新能源承载能力，为电网规划提供指导。部分研究还考虑到新能源出力的不确定性[10-12]，对风电、光伏分别建立不确定性概率模型，从而更加准确地模拟新能源出力特性。上述研究仅考虑到了电力系统总体的功率平衡情况，没有涉及到电力系统潮流方面的各种约束条件，没有考虑线路热稳定极限、变压器容量、节点电压等限制因素，因此，不能够较为准确地描述系统的承载能力。部分研究在考虑潮流约束的前提下，进行新能源承载能力分析。如文献[13-15]均利用一定的潮流近似方法，将潮流模型简化为线性规划模型，并加以求解，这些近似方法都存在一定的误差。也有部分研究不进行近似处理，直接采用迭代寻优的方法，如粒子群优化算法[16]、人工鱼群算法[17]、遗传算法[18-19]等，这类方法在迭代过程中进行潮流计算，利用一定的规则淘汰不满足潮流约束的解，这样的处理方式在一定程度上限制了迭代寻优的范围和方向，影响了迭代速度，具有迭代次数多、运算速度慢的缺陷。

针对以上问题，文中提出一种改进的粒子群优化算法，进行新能源承载能力分析，该算法不淘汰不满足潮流约束的解，而是通过引入修正因子的方式，使不满足潮流约束的粒子回到可行解空间中，最终求得电网的新能源承载能力

1 新能源承载能力分析优化模型的建立与求解

1.1 优化模型的目标函数

文中将一个具有N座变电站和若干条线路组成的电力系统作为研究对象。系统中每座变电站等效为一个节点，接有常规机组、新能源机组和负荷。新能源承载能力分析以新能源总出力最大为优化目标，目标函数可为各节点风电、光伏总出力最大为

(1)

式中:Pnew,i为节点i处所接入的新能源机组的出力，为优化模型的决策变量(i=1,2,…,N)。

1.2 优化模型的约束条件

1) 潮流约束：

Pnew,i+PG,i-Pload,i=

(2)

(3)

其中，式(1)等式左侧为节点i注入的有功功率，可为Pi；PG,i为节点i的常规机组出力；Pload,i为节点i的负荷；Qi为节点i注入的无功功率，主要由电容器提供；Bi为与节点i相连的所有支路对侧节点编号组成的集合；Ui、Uj分别为节点i和节点j的电压幅值；θij为节点i和节点j的电压相角差；Gij、Bij分别为节点导纳矩阵中第i行第j列元素的实部和虚部。

2) 支路功率约束：由于电流具有热效应，因此线路所能流过的电流存在一个热稳定极限电流iij,max，相应的，各支路的有功功率Pij均不能超过线路所能承受的热稳定极限功率Pij,max，即

Pij≤Pij,max。

(4)

3) 节点电压约束：各节点i的电压幅值Ui均不能超过节点电压规定的上限Ui,max和下限Ui,min，即

Ui,min≤Ui≤Ui,max。

(5)

4) 节点功率约束：每座变电站均等效为节点，每个节点注入的视在功率为

Si=Pi+jQi。

(6)

视在功率Si不能超过主变容量Si,max，节点功率约束可表示为

(7)

1.3 基本粒子群算法

粒子群算法(Particle Swarm Optimization,PSO)模拟鸟群的捕食行为，是一种基于迭代的优化算法，以t表示当前迭代次数。首先形成具有M个粒子的种群，每个粒子具有一定的位置Pi,m(t)和速度Vi,m(t)，粒子的位置代表一个可行解 (m=1,2,…,M)。该位置的目标函数值F(Pi,m(t))称为适应度。粒子的位置和速度矩阵表示为

(8)

(9)

在第t次迭代中，所有粒子知道自己当前的位置Pi,m(t)和自己找到的最优位置，即局部最优位置Pi(t)；同时，根据各粒子的适应度，也知道整个群体中所有粒子找到的最优位置，即全局最优位置g(t)。所有粒子追随这两个最优位置按照式(10)更新自己的速度，按照式(11)更新自己的位置：

Vi,m(t+1)=wVi,m(t)+c1r1(Pi(t)-

Pi,m(t))+c2r2(g(t)-Pi,m(t)),

(10)

Pi,m(t+1)=Pi,m(t)+Vi,m(t+1),

(11)

式中:w为惯性因子；c1、c2为学习因子；r1、r2为随机数。

1.4 粒子群算法的改进

现有研究将粒子群算法应用于新能源承载能力分析时，考虑到系统潮流的约束条件，通常将更新得到的节点功率Pi,m(t+1)代入潮流方程，得到系统中的所有支路功率和节点电压，使用支路功率约束和节点电压约束对粒子更新后的位置进行校验，淘汰不满足约束条件的粒子。这样的处理方法需要的迭代次数较多，影响计算速度。针对这一不足，文中提出改进的粒子群算法，改进的原则是不淘汰越限的粒子，而根据越限的情况修正粒子的位置，使越限的粒子回到可行解空间中来。修正过程包括各节点的功率修正和电压修正。

1.4.1 功率修正

粒子找到新的位置后，根据支路功率约束，修正各节点有功功率。对任意节点i，可能会出现节点功率越限，也可能出现与之相连的某条支路功率(对侧节点j)越限。若出现越限情况，则说明Pi,m(t+1)超出了可行解空间，需要对位置Pi,m(t+1)进行修正，使之回到可行解空间中。式(11)表示粒子位置的更新，粒子位置超出了可行解空间，表明位置更新幅度偏大，即速度Vi,m(t+1)偏大。为了使Pi,m(t+1)回到可行解空间，文中引入修正系数，以减小更新幅度，式(11)修正为

Pi,m(t+1)=Pi,m(t)+kVi,m(t+1),

(12)

式中:k为修正系数，该系数的取值取决于粒子的越限程度。若支路功率越限，则k可以通过越限支路功率Pij与该支路功率限额Pij,max的比值进行描述；若节点功率越限，则k可以通过越限节点功率Si与节点功率限额Si,max的比值进行描述。若同时出现两种越限，则k取其中较小者。综上所述，k的表示为

(13)

对于没有出现功率越限的节点，仍按照式(9)更新位置。将式(13)代入式(12)，并与式(11)联立，可得修正后的位置更新公式如下：

Pi,m(t+1)=

(14)

其中C为存在功率越限的节点组成的集合。

1.4.2 电压修正

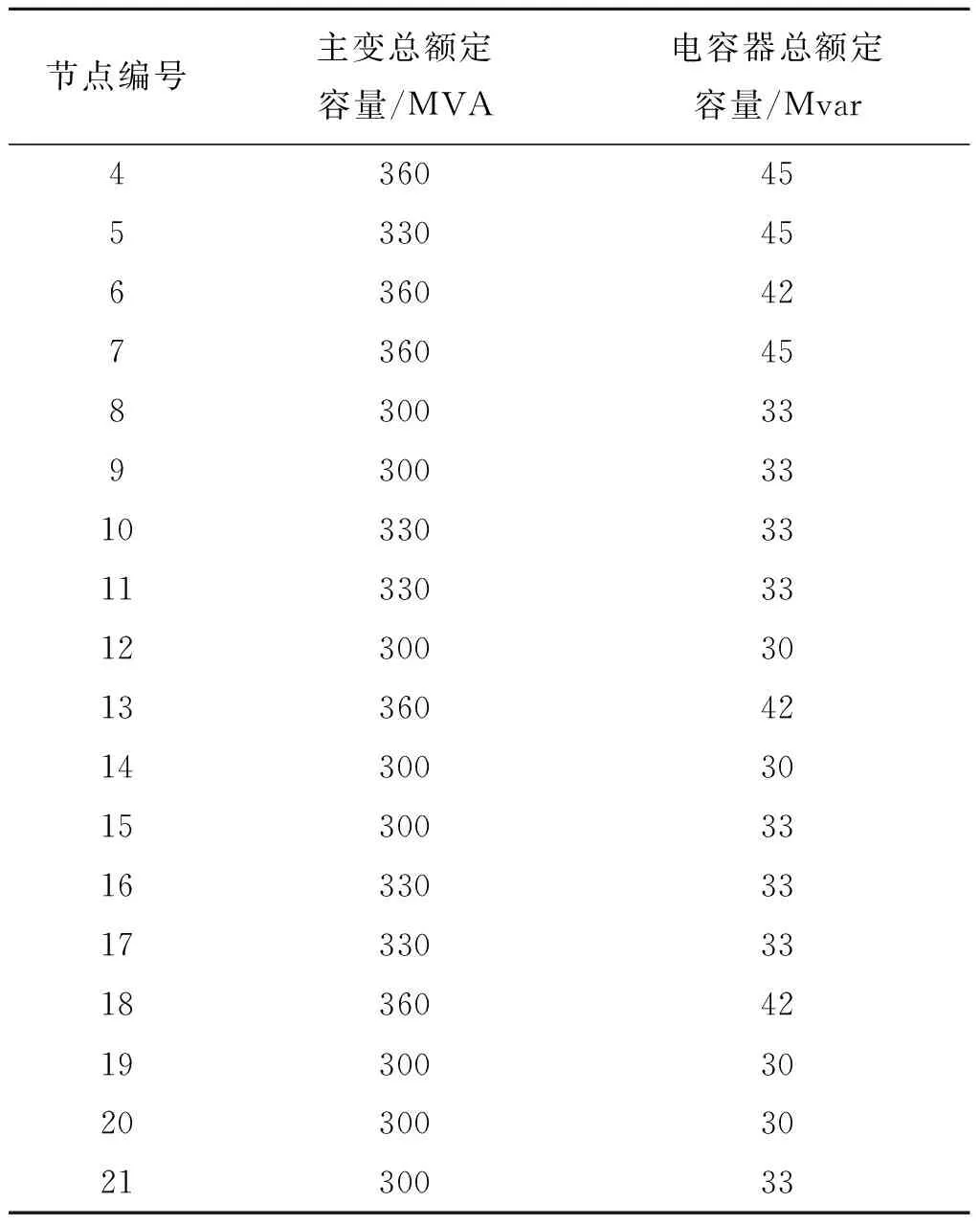
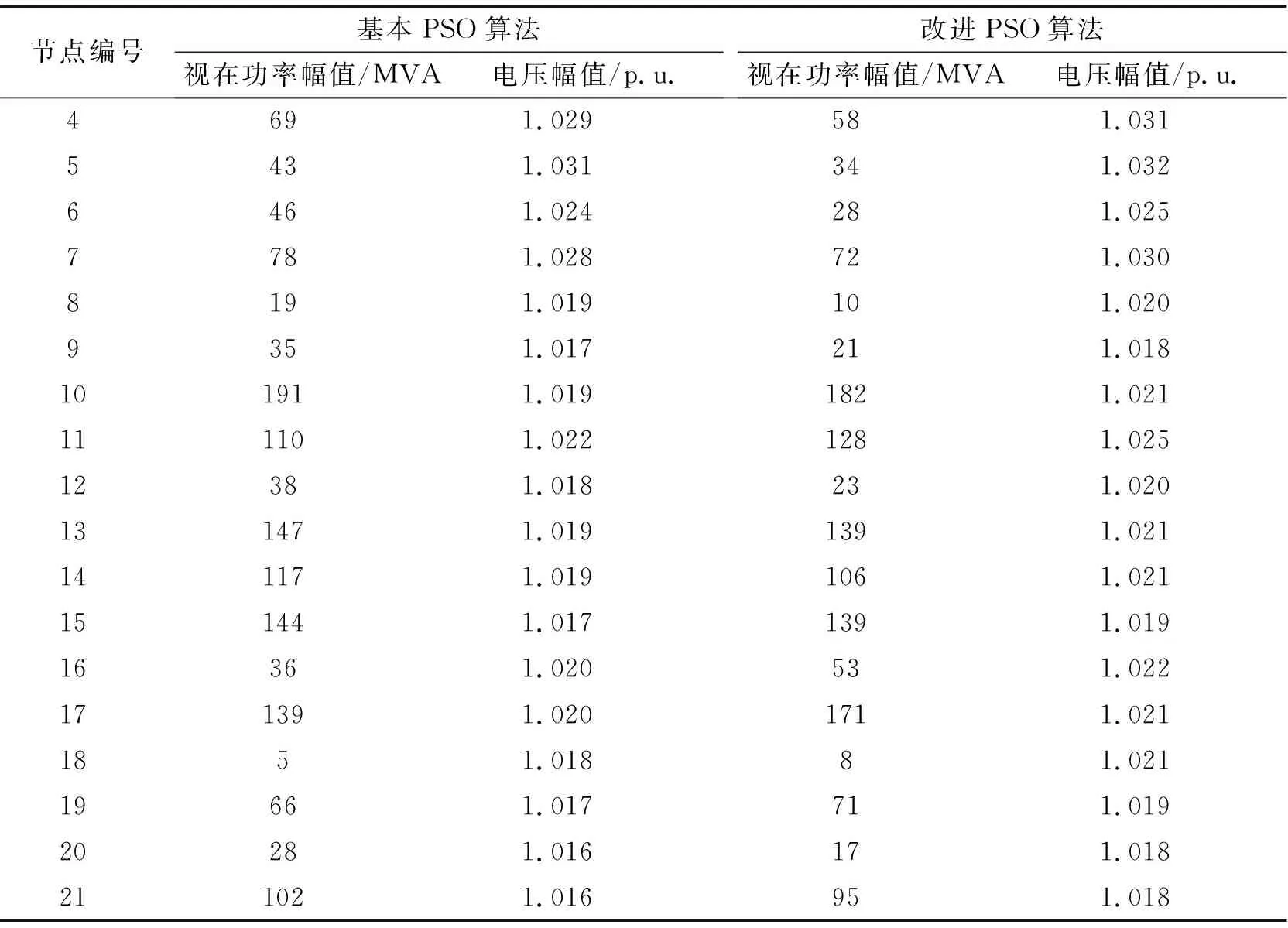
有功修正之后，还需要根据节点电压约束，修正各节点的无功功率。对任意节点i，若电压越上限(即Ui>Ui,max)，则通过退出该节点电容器的方式减小无功功率的注入，直至电压符合要求为止；若电压越上限(即Ui

1.5 改进粒子群算法流程

根据1.4中所述粒子群算法的改进过程，建立算法总流程，具体步骤为

① 初始化种群，并设置粒子群优化算法的参数，包括粒子数M，惯性因子w，学习因子c1、c2，令t=0。

② 计算各粒子对应的目标函数值，作为适应度，根据每个粒子的适应度值，求出粒子i的个体最优位置Pi(t)和全局最优位置g(t)。

③ 根据式(10)更新各粒子的速度，根据式(11)更新各粒子的位置。

④ 根据每个粒子的位置Pi,m(t+1)进行潮流计算，得到与之对应的节点电压和节点功率、支路功率。

⑤ 对所有粒子，判断是否存在功率越限的节点，若不存在，转入⑦。

⑥ 对存在功率越限的粒子进行功率修正，采用式(14)重新更新位置，返回④。

⑦ 对所有粒子，判断是否存在电压越限的节点，若不存在，转入⑨。

⑧ 对存在电压越限的粒子进行电压修正，投入或退出电容器，返回④。

⑨ 判断是否满足收敛条件|g(t+1)-g(t)|<ε(ε是一个很小的数)，若不满足，t=t+1，返回③，开始下一轮迭代。

⑩ 输出最优解，即最大承载能力。

2 算例分析

2.1 算例基本条件设置

文中以某地区220 kV电网为例，进行承载能力分析。该电网包含3座500 kV变电站和18座220 kV变电站，系统结构如图1所示。

图1 系统结构接线图

图1中，节点1，2，3为500 kV变电站中压侧母线，不接入新能源电厂，其他节点为220 kV变电站高压侧母线，均可接入新能源电厂。火电机组G1(装机容量640 MW)、G2(装机容量230 MW)分别通过节点16，14并网。节点1与外部电网联络，视为平衡节点，其他节点视为PQ节点。各220 kV变电站均带有负荷，500 kV变电站则不带负荷。图1中同时标出了各220 kV变电站的负荷，图中单位为MW。

表1所列为各变电站主变及电容器的总额定容量。表2中列出了部分线路的热稳定极限功率。除表2中所列线路之外，所有线路热稳定极限功率均为480 MW。设置粒子总数M=50，学习因子c1=c2=2，惯性因子w=0.5。

表1 主变及电容器总额定容量

表2 部分线路热稳定极限功率

2.2 新能源承载能力计算

文中分别采用改进PSO算法和现有基本PSO算法对2.1中电网进行新能源承载能力计算，并对结果进行比较。

2.2.1 计算结果和迭代过程对比

表3列出了使用两种方法进行新能源承载能力计算，得到的电网新能源承载能力。从表3可以看出，使用改进PSO算法，得到的新能源承载能力分别为2 919.79 MW，比使用基本PSO算法得到的新能源承载能力(2 840.93 MW)提高7.3%。节点17最多可接入新能源电厂容量最高，达到421.84 MW，节点11，16，19也可接入较大容量的新能源电厂，在今后的电网规划中，应尽可能多地在以上节点处安排新能源并网。