一种低频段小型化带通频率选择表面天线罩设计*

王义富，陈毅乔，毛 玮

(中国西南电子技术研究所，成都 610036)

0 引 言

频率选择表面(Frequency Selective Surface，FSS)是一种具有空间滤波特性的二维周期阵列结构，因其具有频率选择透波特性，被广泛应用于微波器件、电磁屏蔽防护、多频天线系统和雷达天线罩等多个领域。

FSS的电磁传输特性是工程应用中的关键性能指标。理想的FSS频率响应为：带内具有平坦高透波性能，而带外应具有陡峭截止特性；此外，还应有良好的角度稳定性、极化稳定性以及带宽特性。带通型FSS是一种具有工作带内透波和工作带外陡峭截止特性的空间滤波结构，可通过多层FSS级联结构来展宽工作带宽并获得高阶滤波特性。因此，带通型FSS在实际工程应用中非常广泛[1-3]。

然而，传统FSS(含带通型)是基于金属单元的电磁谐振特性工作的，导致其单元尺寸与工作波长相当。如果FSS单元尺寸过大，则直接造成有限尺寸内FSS排布数量达不到近似周期性要求,导致FSS存在角度稳定性变差、强散射栅瓣以及大曲率排布困难等问题。因此，亟需开展低频段带通型FSS的小型化设计技术研究。

目前，已有众多学者开展了FSS的小型化技术研究，其中最具代表的是FSS的分形设计和集总元件加载设计等小型化设计技术[4-5]。文献[4]采用分形设计技术将FSS单元尺寸缩减至工作波长的1/7～1/8，提高了FSS的空间利用率。文献[5]通过在FSS上加载集总电容，将FSS单元的尺寸减小至工作波长的8.2%，提高了谐振频率和传输特性等随入射角的稳定性。文献[6-7]提出了一种基于非谐振单元的小型化和低剖面的带通型FSS，与传统的缝隙结构谐振型FSS不同的是，该结构采用非谐振金属贴片单元和金属网格单元交替组合，可以实现高阶带通透波特性。特别说明的是，该FSS单元尺寸可降低至0.1λ0(λ0为中心工作波长)左右，天线罩剖面可减小至(N-1)λ0/30(N为滤波阶数),其小型化和低剖面特性为低频段(L、S和C频段)带通型FSS设计提供了新的设计思路。

针对低频段带通FSS的单元小型化应用需求，本文采用文献[6]提出的非谐振FSS单元结构，开展了S频段二阶带通型FSS电路设计。在此基础上，进一步采用了介质加载和交叉曲折等FSS单元小型化设计技术，成功实现了一种S频段二阶带通型FSS天线罩，FSS单元尺寸缩减至中心工作波长的6.1%左右。此外，本文进一步开展了天线罩实物加工和测试，验证了该设计方案的可行性。

1 电路模型与理论分析

文献[6-7]提出的基于非谐振单元的二阶带通型FSS结构如图1所示。该结构由金属贴片、金属网格和金属贴片三层金属图案组成，金属图案之间采用厚度为h1和h2介质基板隔开。金属贴片和金属网格均为正方形单元，单元周期均为p。金属贴片边长为a，金属网格为宽度为w。

图1 基于非谐振单元的二阶带通FSS结构

基于非谐振单元的二阶带通型FSS单元可采用电路理论进行等效，即正方形金属贴片可等效成并联电容，金属网格可等效成并联电感，如图2(a)所示。当介质基板电厚度h远小于工作波长λ0(h<λ0/12)时，其可采用传输线模型等效成串联电感和并联电容，如图2(b)所示。等效电容和电感分别为C=ε0εrh/2，L=μ0μrh，其中ε0和μ0分别为自由空间介电常数和磁导率，εr和μr为介质基板的相对介电常数和相对磁导率。通过整理合并，可得到图2(c)所示的二阶带通并联电感耦合式滤波器电路[6]。

图2 基于非谐振单元的二阶带通FSS结构

由变换过程可知，

(1)

(2)

2 滤波电路及FSS单元小型化设计

2.1 S频段二阶带通FSS电路设计

设计的S频段耦合式带通滤波器电路参数为：中心工作频率f0=2.15 GHz，相对带宽δ=25%。频率响应选用二阶巴特沃斯滤波器电路参数。负载阻抗为Z0=377 Ω。介质基板采用介电常数为εr=3.5的介质材料(无磁性，μr=1)。

由二阶带通耦合式滤波器参数查表可知[8]，二阶巴特沃斯滤波器的归一化品质因数q1=q2=1.414 2，归一化耦合系数k12=0.707 1。

参考文献[8]，可求得图2(c)二阶带通并联电感耦合式滤波器的电感Lm=900.3 pH，La=Lb=4.19 nH，CI=CII=1 110.7 fF，介质基板厚度h1=h2=3.3 mm。再由公式(1)和(2)便可求得C1=C3=1 059.0 fF。

下一步利用上述电路参数对该滤波器电路进行传输性能仿真计算，结果如图3所示。可以看出，该电路在2.15 GHz出现了明显的透波通带，-3 dB的带宽为25.6%(1.86～2.41 GHz)，与设计要求基本一致。其反射曲线出现了两个谐振极值点，表明该电路具有二阶带通谐振滤波特性。同时，1.6 GHz以下和2.63 GHz以上电磁波的截止特性均大于10 dB，具有较为陡峭的带外截止性能。

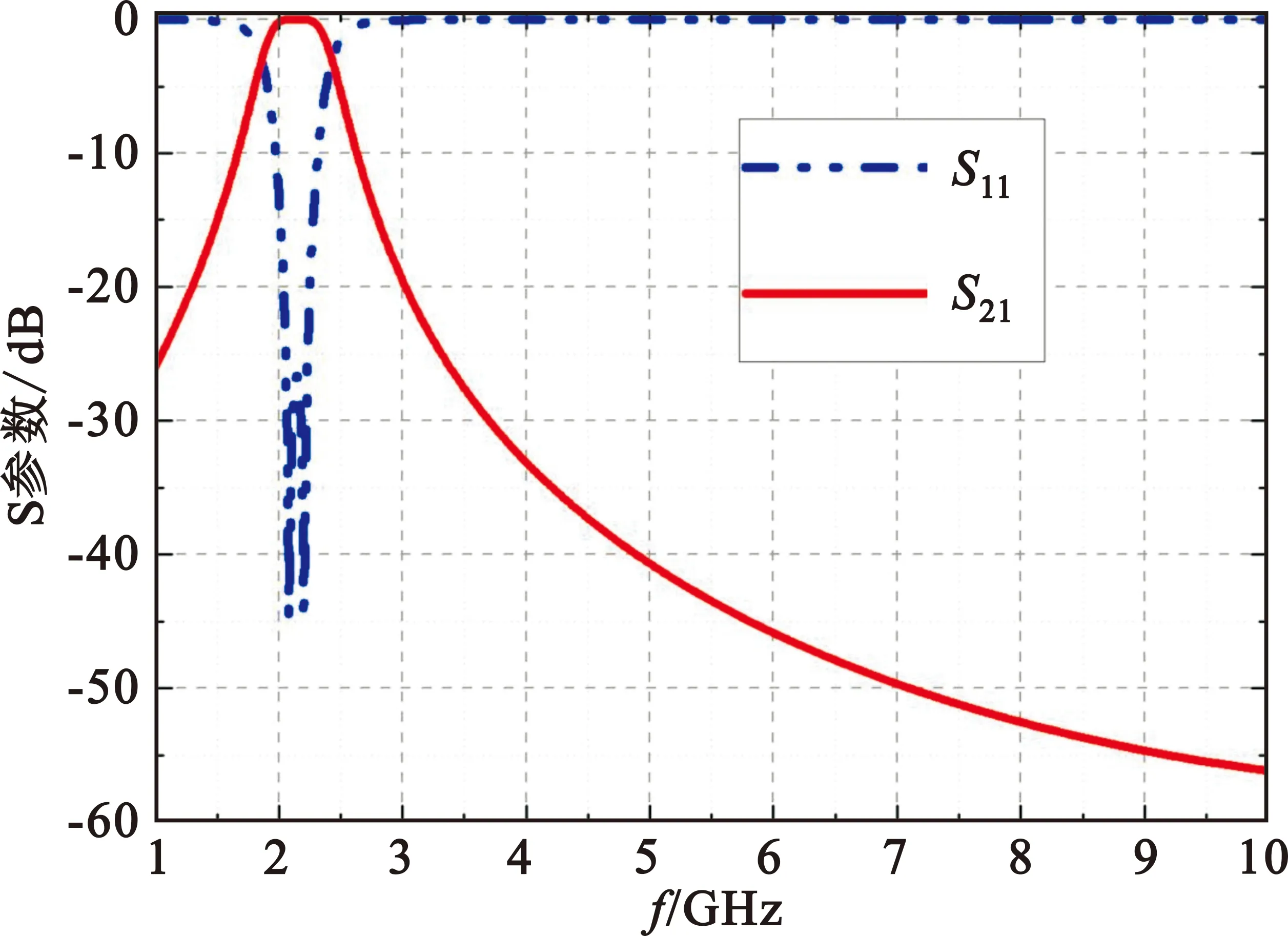
图3 二阶带通FSS的等效电路计算曲线

2.2 FSS结构设计与仿真

获得S频段二阶带通FSS电路后，下一步需将等效电路转化成FSS结构以及物理尺寸等信息，并进行电磁全波仿真验证。

文献[9]提出了一种基于全波数值仿真和微波网络理论精确提取介质中任意形状FSS等效电容和电感的方法，从而建立FSS结构与等效电路的对应关系。

由2.1节可知，介质基板的介电常数εr=3.5，厚度h1=h2=3.3 mm，取容性金属贴片的缝隙g=p-a=0.1 mm(选取原因在后文说明)。采用文献[9]的方法，分别提取介质基板中单层金属贴片和金属网格等效电路参数，从而得到FSS结构。然而，该方法忽略了FSS金属图案之间的耦合影响，使得二阶带通FSS的实际等效电路参数与设计值存在微小偏差，导致全波仿真结果与等效电路理论值有误差。为了抵消互耦影响，本文将在设计值的基础上对金属贴片和金属网格结构参数进行小范围微调和优化，使全波仿真结果与等效电路曲线基本吻合。

利用上述方法，可得到容性金属贴片的尺寸参数：p=16.1 mm，a=16 mm；感性金属网格的尺寸参数：p=16.1 mm，w=6.9 mm。基于上述参数，建立FSS单元的有限元法全波仿真模型，利用Floquent周期性边界条件对整个FSS传输系数和反射系数进行仿真，结果如图4所示。由图4可知，仿真曲线(仿真优化前)与等效电路曲线存在频率偏移，原因已在前面进行了分析和说明。于是，进一步对FSS参数进行小范围局部优化，优化后的FSS结构为：周期p=16.3 mm，金属贴片宽度a=16.2 mm，金属网格w=6.7 mm，参数优化前后的变化率小于3%。可以发现，优化的FSS的全波仿真曲线与理论曲线基本一致，达到设计要求。

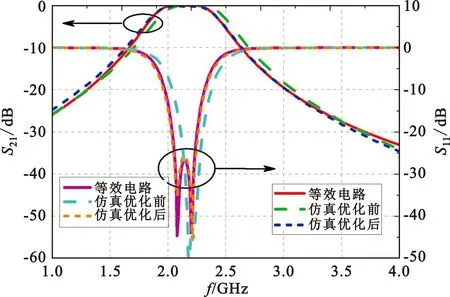
图4 二阶带通FSS的仿真曲线对比

2.3 FSS小型化设计

2.3.1 小型化设计思路

FSS单元的小型化设计即在保持谐振频率不变时，实现FSS单元的周期尺寸的小型化。而对于本文而言，即金属贴片的等效电容和金属网格的等效电感在满足2.1节电路设计值(C1=C3=1 059.0 fF，Lm=900.3 pH)的基础上，实现金属贴片和金属网格单元周期的小型化。

FSS的等效电路可采用静电磁学原理进行分析。对于非磁性材料，FSS的等效电感值取决于FSS金属线结构，与介质材料介电常数无关。对于距离为d的两平行线，若直径和长度分别为a和l，则其等效电感为l/π·ln(d/a)[10]。而FSS的等效电容可采用平板电容器模型进行分析，即电容C正比于FSS附着材料的等效介电常数εr和面积A，而反比于距离d(C=ε0εrA/d)。进一步对本文的FSS结构研究发现：

(1)金属网格的等效电感随网格结构尺寸的调节范围较大。小型化设计时，通过调控金属网格的宽度可以获得设计所需的电感值。例如，当单元周期p取16.1 mm时，取金属网格宽度w=6.90 mm，则金属网格的等效电感为900.3 pH；而周期p缩减至8 mm时，金属网格宽度w减小为2.57 mm，也能获得相同的等效电感值。

(2)金属贴片的等效电容与贴片之间的缝隙宽度成反比，与贴片周长成正比，也与附着介质材料密切相关。在上例中，方形金属贴片之间缝隙选取为0.1 mm时(考虑加工精度)，周期需大于16.1 mm，其电容才可大于1 059.2 fF，难以满足FSS小型化需求。

针对上述分析，本文FSS小型化设计主要针对金属贴片的等效电容而展开，将从介质材料加载、FSS图案缝隙形状设计等方面实现金属贴片的小型化。

2.3.2 介质材料加载

根据平板电容器模型，FSS等效电容正比于FSS附着材料的等效介电常数。当FSS结构固定时，加载介质材料介电常数越高，材料越厚，其等效电容也越大。

表1为方形金属贴片FSS(p=10 mm，a=9.5 mm)在不同介质环境中提取的等效电容参数。可以看出，一侧加介质材料，其等效电容值为322.09 fF。而在FSS另一侧加厚度为0.3 mm的介质后，可将等效电容提高到420.2 fF，电容值增加了30%左右；当介电常数增加到10时，其等效电容可提高1 133.3 fF，效果非常明显。在本例中，材料介电常数选取为3.5，则在金属贴片空气一侧加载0.3 mm介质材料，提高其等效电容。

表1 材料加载对FSS等效电容的影响规律

2.3.3 FSS图案小型化设计

金属贴片FSS单元的等效电容是由相邻金属贴片的缝隙耦合产生的。当金属贴片单元尺寸固定时，缝隙越小，缝隙周长越长，其等效电容越大。因此，通过调节缝隙宽度和周长，可增加其电容耦合量，提高金属贴片的等效电容。

当金属贴片周期为10 mm，两侧加载εr=3.5的介质(厚度分别为6.6 mm和0.3 mm)时，提取得到的等效电容随缝隙g的调制曲线如图5所示。可以看出，通过将相邻金属贴片的缝隙由2 mm减小至0.1 mm，其等效电容由160.6 fF提高至766.1 fF。考虑到加工精度并提高缝隙的等效电容，这里取g=0.1 mm。

图5 周期为10 mm的方形FSS等效电容随缝隙的调制曲线

为了进一步提高金属方形贴片的等效电容，将采用FSS图案的交叉曲折设计技术，在保持金属贴片面积不变基础上，增加缝隙周长，从而增加耦合电容。如图6所示，固定周期(p=10 mm)和缝隙(g=0.1 mm)不变，通过在相邻两侧设计凹槽结构，而在对角侧边设计金属枝节结构，形成缝隙结构的交叉曲折缠绕设计。分别设计一次和二次交叉曲折的凹槽和枝节结构，可以形成一次交叉曲折结构和二次交叉曲折结构，如图6(b)和(c)所示。

图6 FSS图案小型化设计示意图

表2给出了方形贴片、方形贴片一次交叉曲折和二次交叉曲折结构的等效电容，可以看出，通过一次交叉曲折设计，FSS单元由方形贴片的766.1 fF提高到1 061.9 fF，等效电容增加了38.6%；而通过二次交叉曲折设计，等效电容提高到1 207.8 fF，提升效果明显。

表2 不同贴片的等效电容(Lt1=Lg1=2.45 mm,Lt2=Lg2=1.05 mm,Wg1=2.7 mm,d=2.5 mm)

2.4 FSS小型化设计后仿真验证

采用方形贴片二次交叉曲折结构设计了S频段小型化二阶带通型FSS，结构如图7所示。其中，缝隙宽度取0.1 mm，外层介质和内层介质厚度为0.3 mm，介电常数为3.5。

图7 小型化天线罩结构示意图

采用2.2节相同的设计方法，得到小型化后的FSS结构参数，如表3所示。

表3 S频段二阶带通FSS小型化设计后的结构参数

采用基于Floquet 模式的有限元全波分析方法，对小型化后的FSS单元结构进行数值仿真计算，其法向传输特性随频率变化曲线如图8(a)所示。为了便于对比，图中还给出了等效电路设计曲线和小型化前的仿真曲线。由图可知，采用小型化后的法向仿真曲线与等效电路的计算曲线重合较好，达到预期设计结果。值得说明的是，通过介质材料加载和FSS单元小型化设计技术，FSS单元的周期由16.3 mm缩小至8.5 mm，缩减了约48%，FSS面积缩减了73%左右，小型化设计效果非常明显。同时，图8(b)给出了小型化设计前后在典型入射角(45°)的TE极化传输系数曲线。对比发现，入射角由0°增加到45°时，小型化设计后的FSS带内透波中心频率由2.15 GHz偏移到2.17 GHz，相对频率偏移0.09%；而小型化设计前的FSS带内透波中心频率偏移至2.28 GHz，相对频率偏移6.1%，导致2 GHz的传输系数下降至-2.6 dB。可以看出，小型化化设计后，其角度稳定性明显变好。

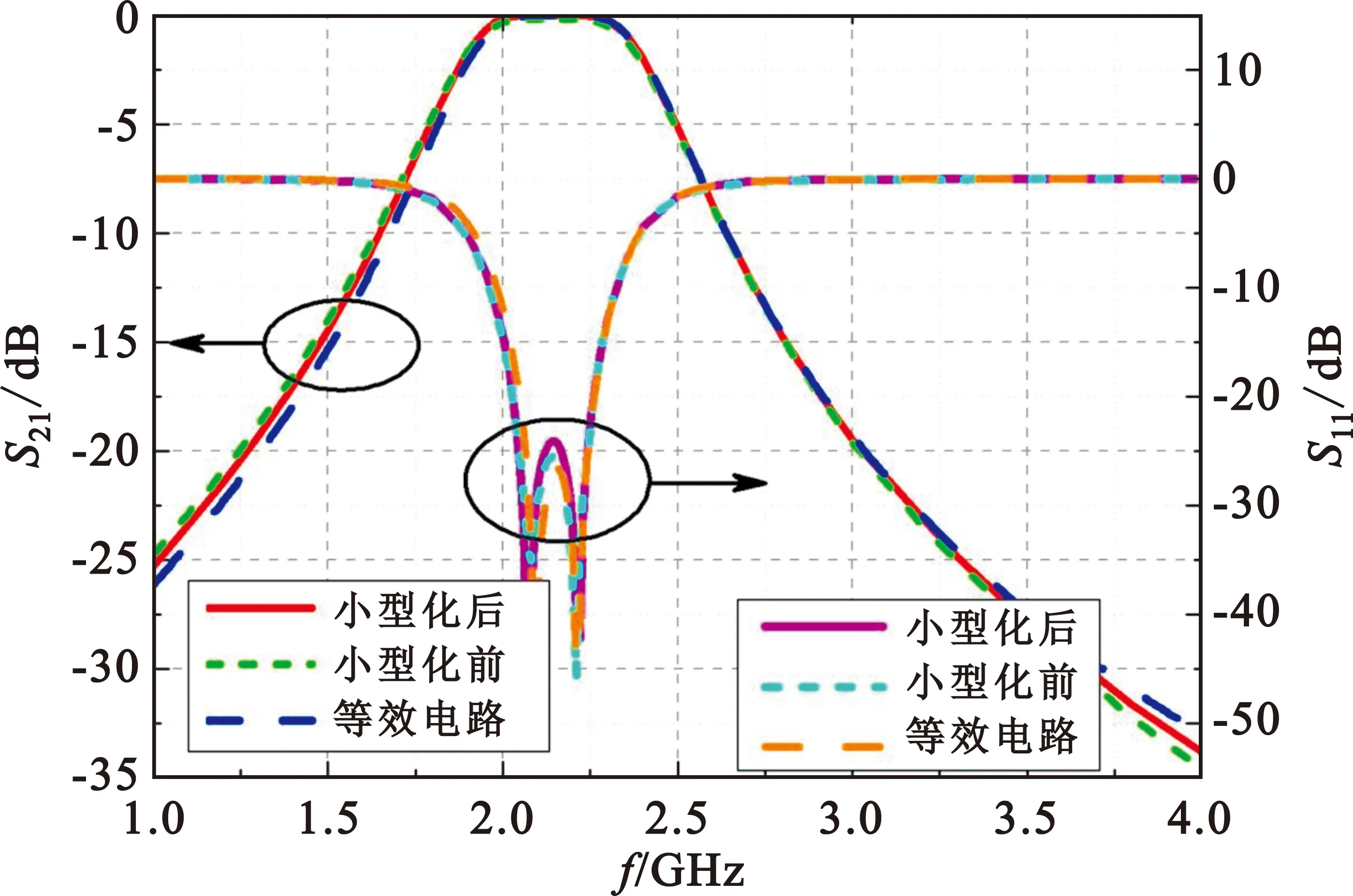
(a)仿真结果与理论曲线对比

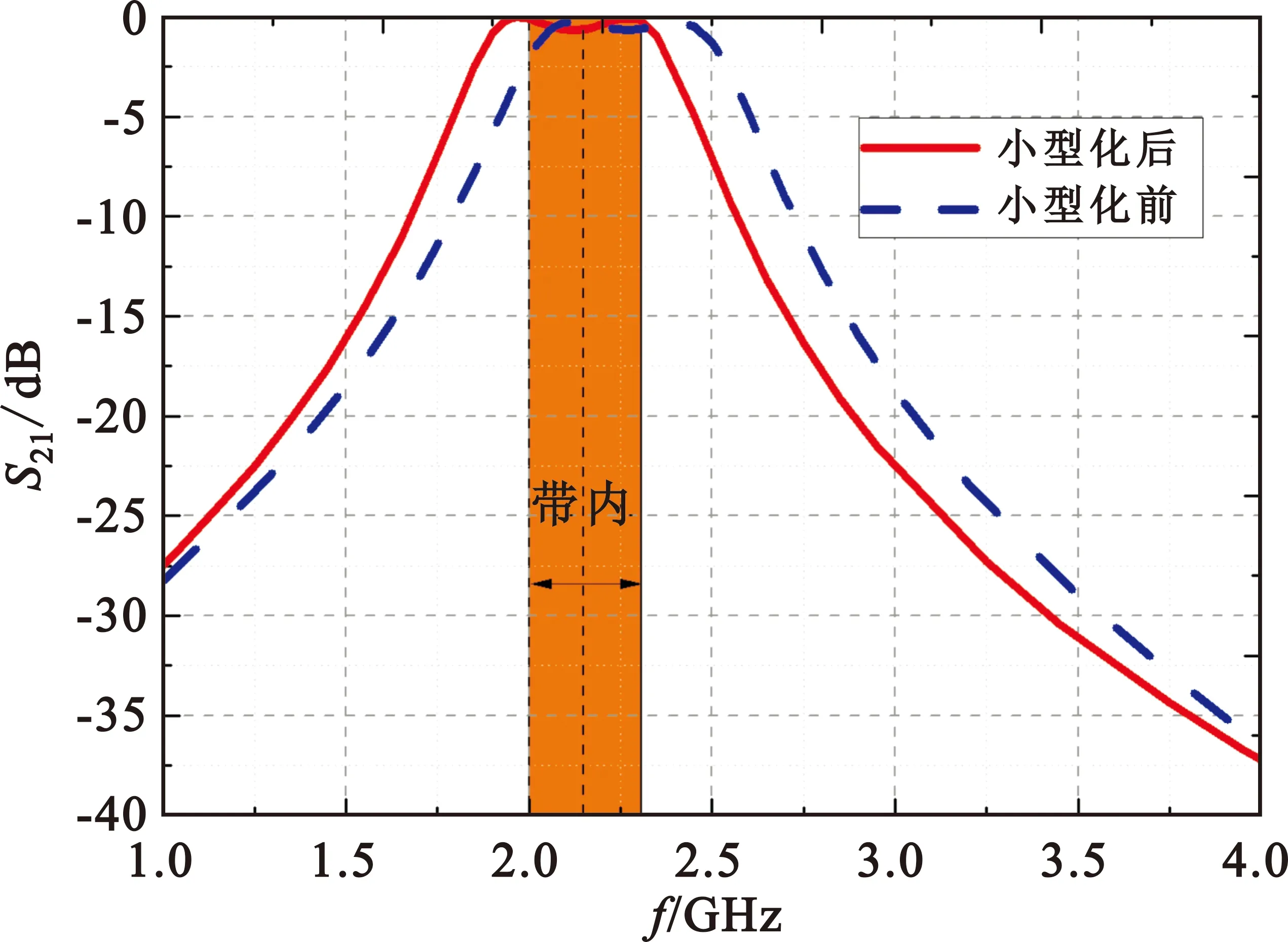
(b)入射角45°的TE波角度稳定性对比图8 小型化设计后仿真结果及对比

3 实物加工和测试

采用多层电路板压接技术加工了S频段小型化后的二阶带通FSS天线罩，如图9所示。介质基板选用泰康公司的PTFE材料RF35TC，其介电常数为εr=3.5，损耗0.005。加工天线罩实物样件大小为200 mm×200 mm，厚度为7.4 mm，厚度偏差为3%，满足厚度偏差要求。

图9 S频段二阶带通天线罩实物样件

天线罩的传输性能测试采用等效平板的测试方法进行。采用两个双脊宽带喇叭天线作为发射天线和接收天线。为了消除环境影响，整个测试在微波暗室完成，并采用时域门测试技术，消除背景的多径反射。

该天线罩的法向测试传输曲线如图10所示，为了进行对比，也一起给出了仿真曲线。可以看出，测试结果与仿真曲线基本一致，带内吻合较好；但带外存在差异，主要是由于带外透射能量较小，天线罩尺寸无法足够大，导致存在边缘效应。总的来说，天线罩达到了预期设计效果。

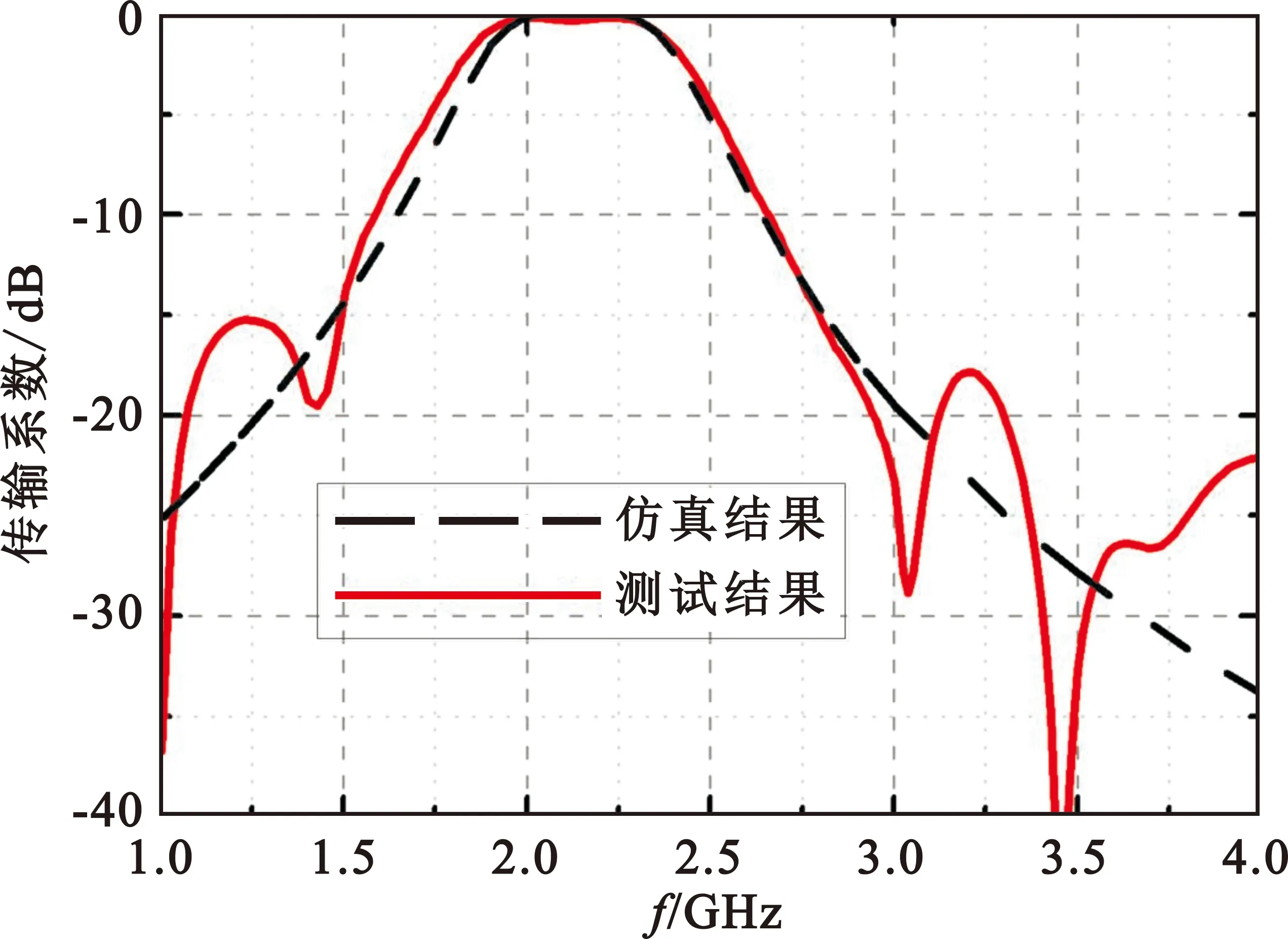
图10 天线罩样件传输系数测试结果

4 结 论

本文开展了低频段具有带通滤波特性的小型化FSS天线罩研究。该FSS天线罩采用金属贴片、金属网格和金属贴片非谐振频选单元的交替排列而成，并通过介质加载和FSS图案的交叉曲折设计技术，使其在S频段具有二阶带通空间滤波特性。完成了S频段二阶带通小型化FSS天线罩的加工和测试，测试结果与设计结果吻合较好，验证了设计的有效性。该方案为低频段隐身天线罩设计提供了技术途径，具有潜在应用价值。