一种应用遗传算法的阵列天线共址干扰抑制技术*
2022-10-28李禹柯
李禹柯
(中国西南电子技术研究所,成都 610036)
0 引 言
在电子信息技术迅速发展的大前提下,搭载无线射频系统的平台正向着高度综合化、标准化、通用化和多功能化方向发展[1]。在有限大的平台上集成包括通信、导航、识别、探测在内的大量具备无线收发能力的功能,必然会面临共址干扰问题。共址干扰一般被定义为同平台上的发射设备通过天线产生的电磁辐射信号被接收设备的天线捕获,从而对接收机性能产生影响的现象。共址干扰会严重影响同平台无线接收设备的正常工作,导致电台通信距离下降、导航失效、二次雷达误应答等问题,严重时可能导致信道阻塞,甚至烧毁接收设备。因此,为了保证电子系统的正常工作,必须针对共址干扰问题进行必要的系统电磁兼容设计。
传统解决共址干扰问题的方法主要包括频率管理、良好的发射机非线性设计、合理的天线布局、恰当的滤波设计[2]。在无线收发设备较少时,这些方法可以保证系统的电磁兼容性,但在无线射频系统日益多功能和复杂化的现在,使用传统方法解决系统电磁兼容问题的成本越来越高。而对于某些新出现的电磁兼容问题,传统方法甚至无法提供有效的解决方案。
自适应自干扰消除(Adaptive Self-interference Cancellation,ASC)技术可以有效地减轻共址干扰带来的影响,其基本思想是:从干扰源提取参考信号,将干扰信号的传输通道由一个可调滤波器近似描述。参考信号经过此可调滤波器后,得到干扰信号的近似信号,将其与干扰信号直接相减即可实现一定程度的干扰抑制。国外对自适应干扰消除开展了大量的研究,并将之应用于实际工程产品。国内的研究人员也对该技术进行了跟踪研究[3-5]。
虽然自适应干扰消除技术可以实现共址干扰的抑制,但这种技术,特别是基于模拟电路的自适应干扰消除技术通常需要增加系统的体积、重量、复杂度和功耗开销。而在存在天线阵列的共址干扰问题中,由于自干扰消除信道数量会以天线数量的平方倍增长[6],系统的复杂度将会达到一个不可接受的程度,这限制了干扰对消技术在阵列天线中的使用。
2017年,麻省理工学院(Massachusetts Institute of Technology,MIT)的林肯实验室提出了孔径级同时收发技术。文献[7-8]中提出了一种基于自适应波束形成的收发隔离技术,通过对每个阵元的发射信号进行调制,使发射阵列在接收天线处的合成信号形成“零陷”来抑制接收机受到发射机的干扰。这种方法避免了设计复杂的模拟自干扰消除网络,仅利用阵列天线已有的接收机结构即可实现干扰抑制。随后,研究者通过基于拉格朗日乘子法的最优化方法实现了理论上的阵列天线干扰抑制。
虽然研究已经证明通过自适应波束形成可以实现收发隔离,但目前对该技术的研究都集中于单一阵列天线的同时收发问题。此外,文献中所采用的加权矢量求解算法需要对天线间的耦合度进行精确测量,这在实际工程应用中会导致干扰抑制能力下降,甚至可能导致干扰的反向增强。本文提出了基于遗传算法的相控阵共址干扰抑制技术,可以解决同平台多个天线孔径间的收发隔离问题,在天线耦合度未知的状态下实现加权矢量的求解,同时可更加灵活地设置约束条件。
1 理论分析
1.1 系统模型
本文分析一种同一平台上同时存在阵列天线发射机和无源天线接收机的场景,这种场景下的同平台共址干扰问题在实际工程应用中频繁出现,具有一定的普遍性。
1.1.1 辐射模型
不失一般性,设平台上存在有J个阵元的线列发射机和K个相互独立的全向天线接收机,发射机和接收机的信号关系如图1所示。
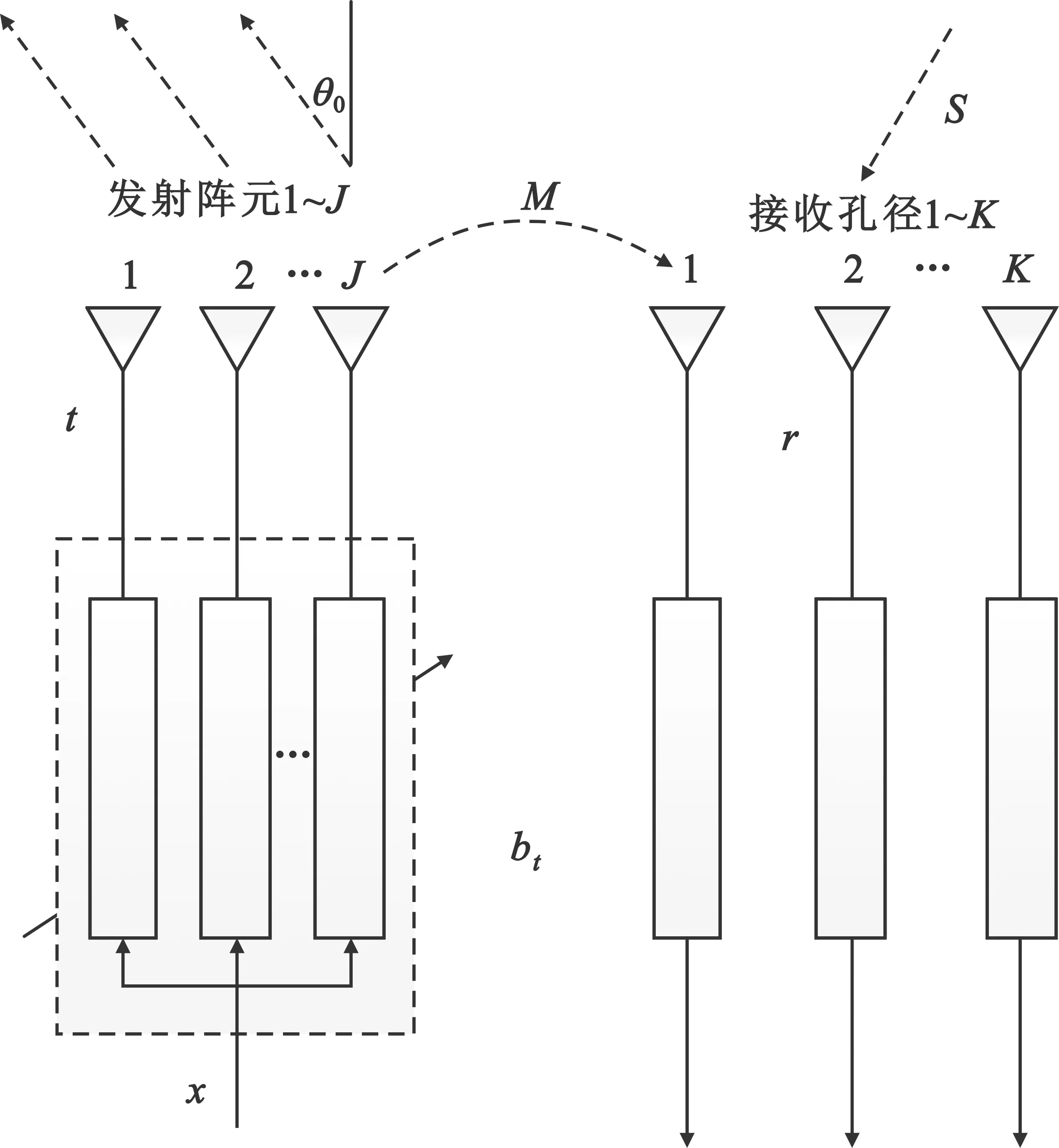
图1 阵列天线发射与接收孔径之间的信号流图
图1中,发射信号x经过波束赋形器后,通过J个发射阵元辐射。t为J维阵列天线的发射信号矢量,可以表示为
t=btx+nt。
(1)
式中:x为需要发送的信号;bt表示发射波束赋形系数矢量,是J维矢量;nt为期望为0的高斯白噪声(Additive White Gaussian Noise,AWGN),表征发射机引入的噪声。
发射信号矢量通过天线阵列辐射,多个天线端口辐射的信号将在空间中产生叠加和抵消,从而体现为在一些方向上增益加强,在另一些方向上增益降低。设阵元间距为d,阵列发射波长为λ,期望获得的波束指向与法线的夹角为θ0,则归一化后波束指向方向的等效全向辐射功率(Equivallent Isotropic Radiated Power,EIRP)可以表示为
(2)

(3)
为了简化公式,对发射信号x归一化,令E[|x|2]=1,并考虑到发射噪声功率远小于发射信号功率,可以得到
(4)
1.1.2 干扰模型
当存在同平台阵列天线发射时,平台上K个全向天线孔径接收信号可以表示为
r=s+Mt+nr。
(5)
式中:r为K维接收信号矢量,K维矢量s代表每个接收天线接收到的外部信号;K×J维矩阵M代表发射和接受阵元之间的耦合矩阵,M第k行第j列的元素m(j,k)表示第j个发射阵元到第k个接收天线孔径的近场耦合响应;K维矢量nr为期望为0的高斯白噪声,代表接收机引入的噪声。

1.2 优化算法
1.2.1 约束条件
文献[7-8]中,发射机与接收天线的优化问题被定义为
s.t. EIRP=EIRPmax。
(6)
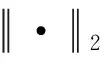
上述优化问题的物理意义为:在等效辐射功率不变的前提下,使接收机接收到的辐射相关信号最小化。这个优化问题的定义在解决本文中的问题时,未对发射波束赋形器的最大增益进行约束,以及求解得到的r最小值与工程的实际需要并不完全匹配。
(1)未对发射波束赋形器的最大增益进行约束
由于阵列天线通常是以其最大辐射功率工作,也就是说,发射波束赋形系数矢量bt在实际工程场景中存在上限,这里将其归一化后表示为
(7)
式中:Diag(*)表示矩阵*的对角元素,Λ表示单位对角阵。
在优化过程中,如果不考虑此约束条件,则可能会产生大于阵列天线实际能力的系数。这样的解在数学上成立,但是实际工程中很难实现。
(2)求解得到的r最小值与工程的实际需要并不完全匹配
r最小化通常意味着发射机的辐射在接收天线孔径上完全相互抵消,但是,由于信道衰落、链路非线性等各种因素影响,最终通过发射波束赋形系数矢量bt的调制可以实现的抵消效果有限,目前能达到的抵消能力为30~50 dB[7]。在这种非理想化的场景中通过以上最优化方法求解后,多个接收机天线接收到的辐射功率相差可能达到20 dB。这将可能产生如下问题:当部分接收天线对应的接收机已经实现了很高的干扰抑制,而其余部分仍然处于饱和干扰的状态。
因此,在本文中,优化问题被重新定义为:共址干扰抑制的目标是在保证不使本平台其他接收机饱和的前提下,最大化发射机输出的EIRP。其数学模型表述如下:
s.t.r≤ssat,
(8)
通过这种定义,可以降低对接收功率不必要的要求,而尽可能保证阵列天线的辐射能力不受到影响。
1.2.2 遗传算法
通过对模型的分析并建立最优化数学模型可以看出,此模型为带约束条件的单目标优化问题,其解空间为发射波束赋形系数矢量张成的线性空间,可以采用遗传算法进行优化。与传统的优化方法相比,采用遗传算法解决本文中提出的优化问题有如下优点:
采用传统的优化方法需要已知M的数值,而为了达到较高的抑制比,对M的精度也提出了很高的要求。在实际应用中,复耦合矩阵M在实际使用中很难被直接测量,且测量结果受到温度、频率等因素的影响,需要实时进行校准。与传统的凸优化方法不同,采用遗传算法进行计算时不需要获取耦合矩阵M的具体数值,只需在给定输入bt时,给出向量r的结果即可进行优化。bt是发射天线阵列的阵因子,可以直接读取;r是接收机的接收信号,可以通过接收链路进行测量。因此,采用遗传算法可以避免引入复杂的耦合矩阵测量流程,且不会受到耦合矩阵的测量误差影响,导致干扰抑制能力下降。
此外,相比起传统的优化方法,采用遗传算法可以更加灵活地处理复杂的约束条件,这种算法可以很好地适应公式(8)中所提出的非线性约束问题。
最后,遗传算法具有很好的可扩展性,可以与其他算法相结合,处理在时间域、空间域上存在紧耦合的复杂优化问题。
遗传算法求解流程如图2所示。

图2 遗传算法基本流程图
2 测试和仿真分析
本节针对某型载具中天线间的耦合问题,采用前文提到的方法进行测试和分析。载具上安装了一副四阵元的均匀线阵,以及两副全向的接收天线,天线排布方位可以抽象为如图3的模型。

图3 某型载具阵列天线共址干扰场景及测试过程
为了进行仿真分析,通过实测的方法获取了发射天线阵列和接收天线之间的耦合矩阵M。将发射天线阵列的4个阵元依次连接至矢量网络分析仪的发射端口,将两个接收天线孔径依次连接至矢量网络分析仪的接收端口,共测量8组数据用于仿真分析。
选取典型频率300 MHz,以上述测试方法对载具的天线耦合矩阵进行实测,可以得到复耦合矩阵M的数值,如表1所示。

表1 复耦合矩阵M的幅度和相位
在测量得到了复耦合矩阵M后,就可以求解特定发射波束赋形矢量bt下式(5)中的向量r,然后用遗传算法求解式(8)中的优化问题。
在遗传算法中,bt中每个阵元被64 b数表示,其中32 b表示实部,32 b表示虚部;种群个数被设置为20个;交叉概率参数为0.8;计算的迭代次数被固定为100次。
根据载具上发射机和接收机设备的特性,归一化后阵列单阵元发射电平为1,两个接收机饱和电平均为0.000 1。
首先分析阵列天线辐射方向分别为0°和45°时的优化结果,如图4所示。可以看出,在阵列辐射角度为0°和45°时,遗传算法都可以在20~30代时收敛到一个稳定的结果。

(a)0°

(b)45°图4 辐射方向分别为0°和45°时的收敛性
将仿真的结果与式(6)中的的优化问题所计算的结果进行了对比。由于这种方法计算结果将会使波束赋形矢量超过实际工程的发射功率上限,因此在本文的仿真计算中,将计算结果进行了等比缩减,以满足最大功率要求,即
(9)
通过式(9)对式(6)的计算结果进行了补偿以后,在天线辐射方向为0°时,相比起未进行优化前两副接收天线分别实现了41.0 dB和33.3 dB的共址干扰抑制;天线辐射方向为45°时此值为36.3 dB和27.9 dB,以上抑制值均可以让接收天线的干扰信号小于其饱和电平。0°和45°时由于干扰抑制带来的EIRP损耗分别为3.41 dB和1.67 dB,而使用传统方法时损耗分别为4.25 dB和1.79 dB。
图5(a)中给出了扫描角度为0°~60°时,采用本方法时接收天线的共址干扰抑制曲线,可以看出在两个接收天线上均实现了30 dB以上的抑制度。而从图5(b)可以看出在所有辐射方向上,本文方法导致的EIRP损失均小于文献[7-8]中的方法。以上仿真证明了本文方法的优势。

(a)共址干扰抑制度(本方法)
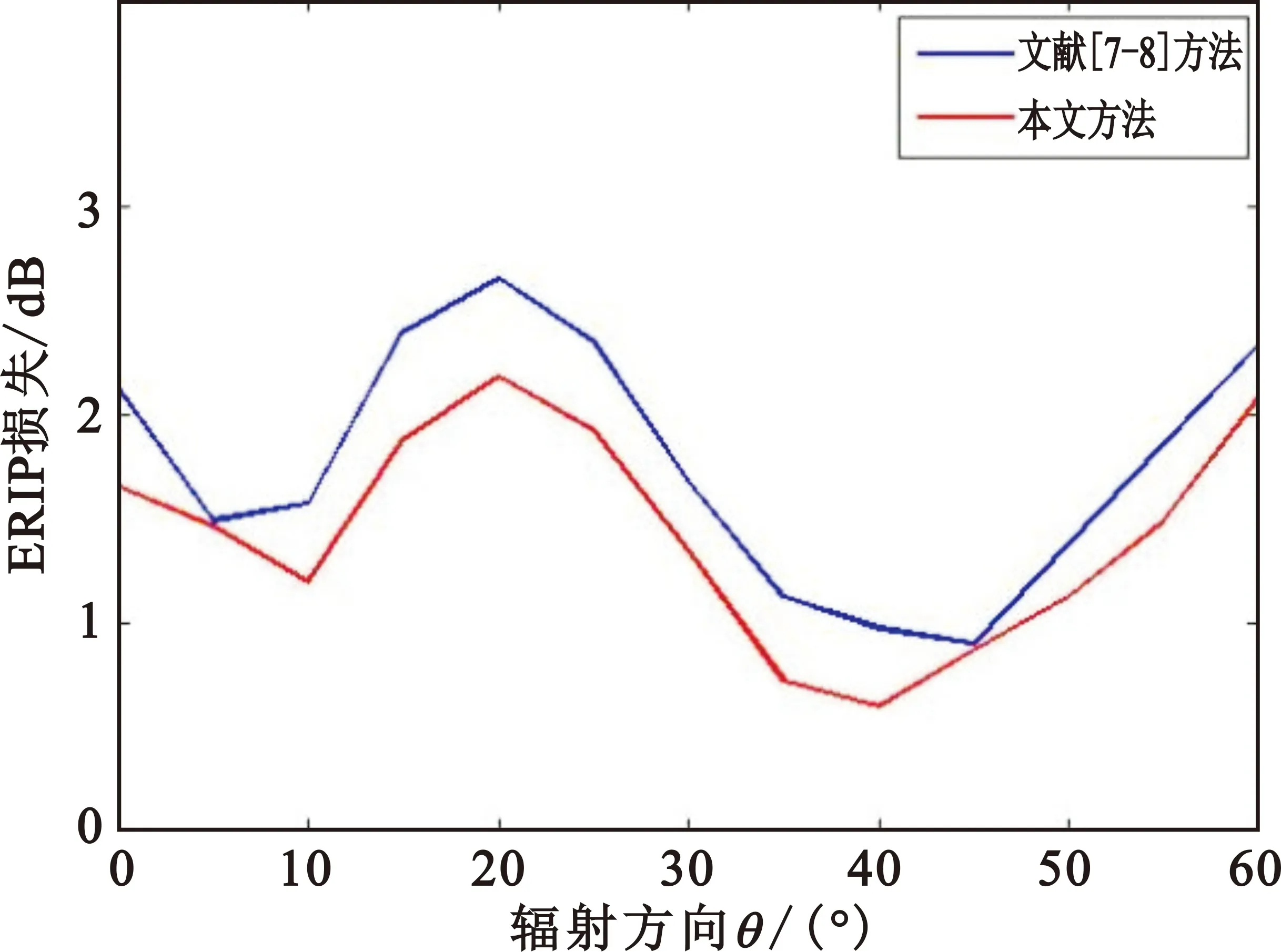
(b)EIRP损失图5 阵列辐射方向为0°~60°时的干扰抑制和EIRP损失
3 结束语
本文针对同平台天线间的共址干扰问题,提出了一种采用智能算法的阵列天线干扰抑制技术。本文从阵列天线共址干扰抑制的实际需求出发,重新设置了优化方案。与已发表的阵列天线同时收发技术相比,这种优化方法可以通过降低不必要的共址干扰抑制需求提升干扰抑制状态下主频辐射的性能;由于采用了遗传算法,本文方法无需获取耦合矩阵信息就可以进行优化计算。由于以上两个特性,本文方法相比文献中的方法更加符合实际工程应用的需求。
对本方法的进一步研究计划包括在真实的载具上实现干扰抑制以及对遗传算法性能的进一步优化等。
