一种基于期望模型的自适应Singer模型滤波算法*
2022-10-28宁静,陈俊,吴麒
宁 静,陈 俊,吴 麒
(中国西南电子技术研究所,成都 610036)
0 引 言
由于目标的运动状态往往无法提前预知,目标机动状态也常常随时间变化,在工程上对机动目标的跟踪要求算法具有较强的机动范围适应性以及较高的实时性等特点。
由于Singer模型[1-4]算法的模型参数反映了目标运动过程的统计特性,在工程上Singer模型常常用于对机动目标进行跟踪,在理论上也涌现了不少基于Singer模型的机动目标跟踪算法。文献[4]提出了一种参数自适应调整的Singer模型跟踪算法,在滤波过程中匹配机动等级来自适应调整Singer模型参数,但这种参数调整方式具有一定主观性,且存在机动等级的跳变,相应地会导致系统的滤波参数发生突变,从而带来跟踪效果的恶化[3]。文献[5]提出了一种IMM-Singer 模型的机动目标跟踪算法,首先设置3组Singer模型组成模型集合,3组Singer模型分别匹配不同的目标机动状态,然后使用交互式多模型(Interacting Multiple Model,IMM)进行滤波。IMM[1-7]算法对三个子滤波器的滤波结果进行交互混合,因此相比较单一模型滤波算法能更好地对目标不同机动状态进行跟踪,但由于其所使用模型集合中的模型参数在滤波过程中不能改变,因此滤波效果好坏取决于模型集合中的模型参数能否覆盖目标机动模式:当模型集合中模型参数能覆盖所有目标机动状态时,跟踪效果较好;当所用模型不能覆盖目标机动状态时,跟踪效果不好。
本文提出一种基于期望模型的自适应Singer模型滤波算法,通过实时计算一个期望模型来动态扩展IMM算法的基础模型集合,实现滤波过程中模型的自适应变化。仿真结果表明,本算法在目标不同机动状态下都可以进行准确跟踪,具有更好的环境适应性,是一种有效的机动目标跟踪算法。
1 基于Singer模型的滤波算法
Singer模型算法[1-4]对目标加速度a(t)作为具有指数自相关的零均值随机过程进行建模,其目标加速度自相关函数为
R(τ)=E[a(t)a(t-τ)]=σ2e-α|τ|。
(1)
式中:σ2表示目标加速度方差,α表示机动频率。σ2和α是待定参数,两者决定了在[t-τ,t]区间的目标机动特性。
(2)
式中:amax为最大机动加速度,P0=P{a(t)=0}表示非机动概率,Pmax=P{a(t)=±amax}表示加速度取最大值时对应的机动概率。Singer模型的状态方程可以表示为
Xk+1=FkXk+Vk。
(3)
其中:
(4)
(5)
式中:T为离散化的采样周期。过程噪声V(k)是均值为0的白噪声,其协方差为
(6)
(7)
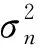
文献[5]提出了IMM-Singer模型算法,选取3个典型Singer模型,每一个模型都对应一个典型的机动频率和过程噪声。模型参数设置如表1所示。

表1 模型参数设置表
基于以上三个Singer模型进行IMM滤波,具体算法步骤可参见文献[5]。该算法结合IMM和Singer模型的算法优势,跟踪性能相比较单一Singer模型有所提高。但是由于模型集合中的模型参数设置是固定的,对机动跟踪效果依赖于模型集合中3个初始模型参数。
2 基于期望模型的自适应Singer模型滤波算法
2.1 期望模型
期望模型算法(Expected Model Algorithm,EMA)[8]的实质是利用一个代表真实模式期望值的期望模型增扩原有模型集。EMA与IMM的核心区别就在于模型集随时间自适应变化,当各个时刻产生新的模型集之后再进行滤波,其滤波过程与IMM算法相同。
设M表示模型集,M(1),M(2),…,M(q)是M的子集,E表示期望模型集,是由q个期望模型构成的:



(8)

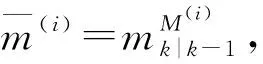
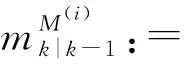

(9)
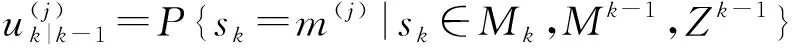

算法k+1时刻的模型集Mk+1为
Mk+1=Ek+1∪(Mk-Ek)。
(10)
k+1时刻得到扩展后的模型集之后,再进行IMM滤波。
2.2 期望模型求解
求解期望滤波模型,即对参与滤波的状态转移矩阵F和噪声协方差矩阵Q进行实时估计,选择最接近目标当前运动模式的模型。根据本文第1节中对Singer滤波模型的分析,F、Q取值受参数α和σ2影响。
在多模型滤波过程中,设定多组与不同机动等级相匹配的参数amax和α,通过实时计算εk,根据εk匹配适合的amax和α,具体为:若γi-1<εk<γi,则选择α=αi,amax=ai,max,变量γ为机动判定门限值,γ可以根据显著性水平通过卡方分布查表获得。进一步通过公式(2)、(5)、(6)计算得到期望模型Fk(α)Qk(α,σ2)。
2.3 滤波算法步骤
参考文献[5]中的模型参数设置,设置3个Singer模型组成基础模型集合,模型设置如表1所示。根据IMM滤波算法原理,不同模型转换服从已知转移概率的有限态马尔科夫链。
扩展模型集合先验概率设置为4个模型概率相同,即ui(0)=1/4,i=1,2,3,4。模型转移概率矩阵Π表示模型之间的转移概率。初值设置原则参考文献[5],对角线元素表示模型不发生切换的概率,应该设置为较大的初始值。模型转移概率矩阵设置如下:


(11)
式中:πij表示模型j转移到模型i的概率。
滤波步骤如下:
Step1 输入混合[1-2]。
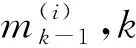
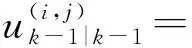

(12)
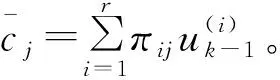
(13)
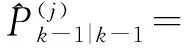
(14)
Step2 模型条件滤波[5-6]。
对于i=1,2,…,4分别计算
(15)
(16)
对于i=1,2,…,4,分别计算
(17)
(18)
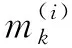
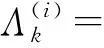
(19)
对于i=1,2,…,4,分别计算
(20)
(21)
(22)
对于i=1,2,…,4,计算
(23)

Step3 输出交互[9-11]。
(24)
(25)
Step4 融合求解模型残差及其协方差。
融合求解模型残差及协方差就是给出k时刻各个模型的总体滤波残差和协方差:
(26)
(27)
Step5 求解期望模型。
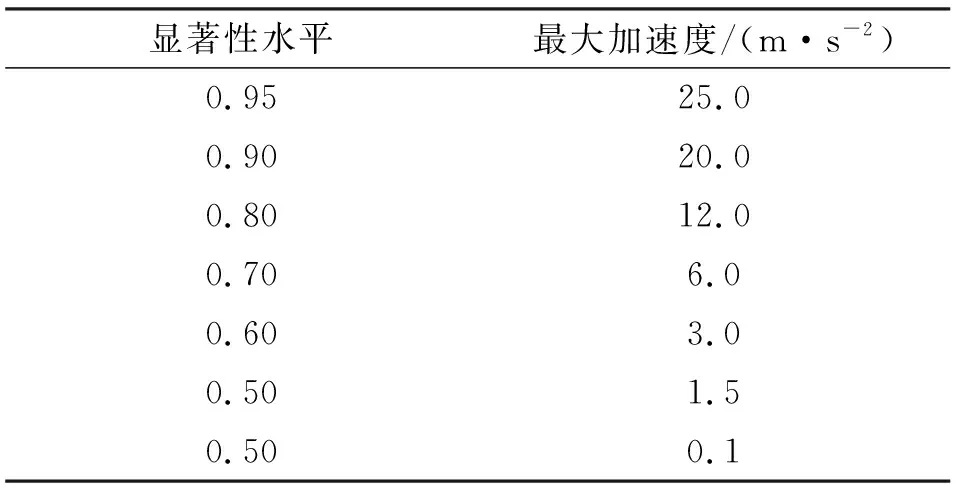
表2 算法参数设置
得到amax和α后,进一步代入公式(2)、(5)、(6)计算期望模型Ek的参数Fk(α)和Qk(α,σ2)。
Step6 扩展模型集合。
算法k时刻的模型集Mk为
Mk=Ek∪(Mk-1-Ek-1)。
(28)
k时刻得到扩展后的模型集之后,再重复上述步骤。
3 仿真与分析
3.1 仿真场景设置

表3 目标运动过程设置
目标任一维度位置量测噪声标准差为50 m,目标x-y平面运动轨迹如图1所示。

图1 目标真实运动轨迹
3.2 结果分析
蒙特卡洛仿真200次,分别使用文献[4]和文献[5]算法与本文所提滤波算法进行目标跟踪,计算算法的位置误差均方根和速度误差均方根,并分别画出算法的误差曲线,如图2和图3所示。
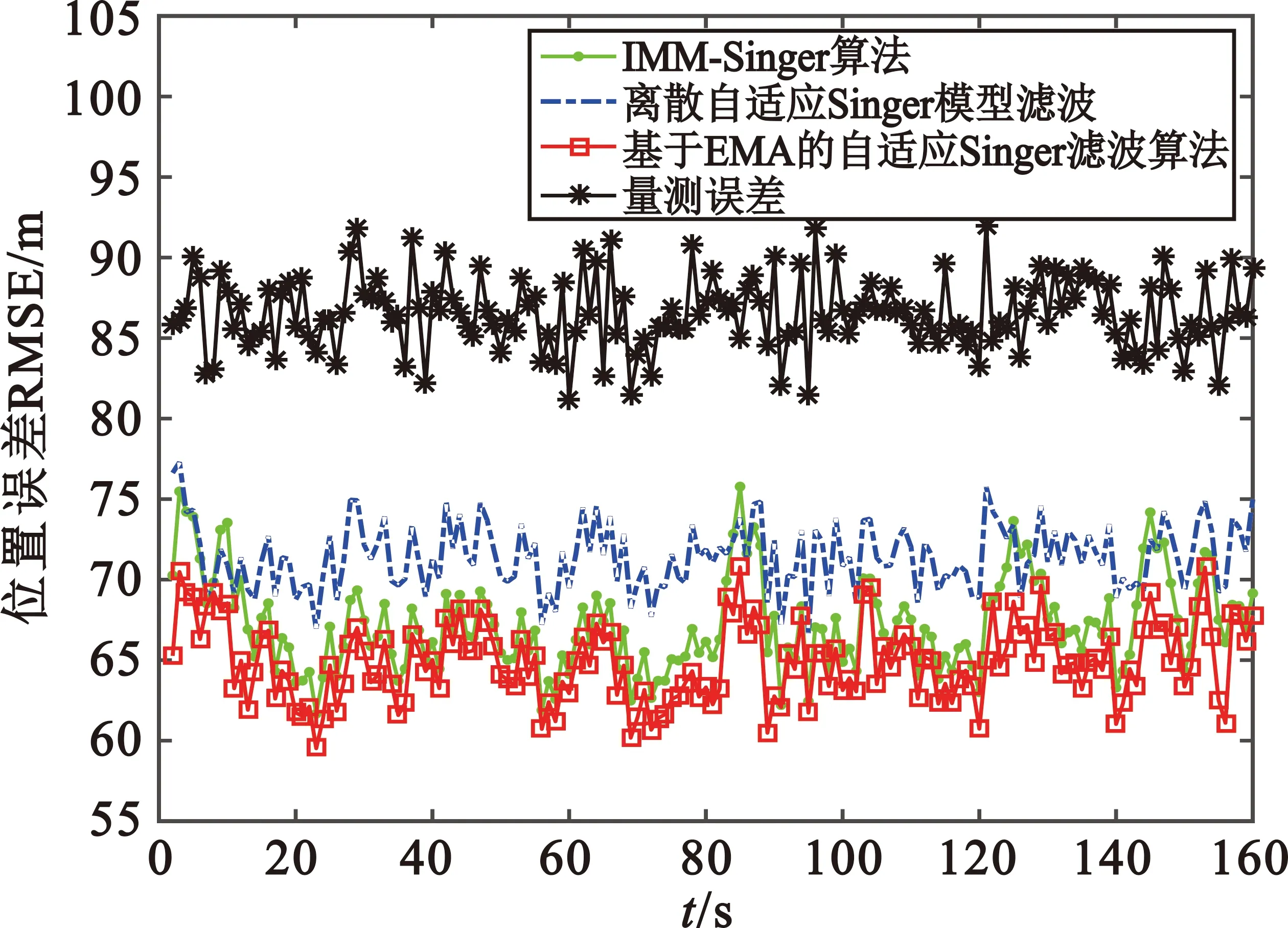
图2 位置误差对比图

图3 速度误差对比图
从图2可以看出,IMM-Singer模型滤波算法和基于期望模型的自适应Singer模型滤波算法对目标位置的估计效果优于离散自适应Singer模型算法,而基于期望模型的自适应Singer滤波算法对目标位置的估计效果优于IMM-Singer滤波模型算法,其位置误差最小。
从图3可以看出,IMM-Singer模型滤波算法和基于期望模型的自适应Singer模型滤波算法对速度的估计效果优于离散自适应Singer模型算法,而基于期望模型的自适应Singer滤波算法对速度的估计效果优于IMM-Singer滤波模型算法,其速度估计误差也最小。
从表4所示的算法跟踪性能对比可以看出,滤波效果方面,文献[4]所提的离散自适应Singer模型算法估计误差最大,文献[5]所提的IMM-Singer模型算法其精度较高。这是因为选取的三个基础模型能比较好地覆盖目标大多数机动情况,通过多模型交互滤波实现机动目标跟踪。但是当目标机动状态与基础模型差距较大时,滤波误差会增大,如在仿真实验中的转弯阶段和加速度切换阶段。本文所提算法在文献[5]算法的基础上,实时检测机动变化,计算期望模型扩充基础模型集合,能更好地应对目标机动状态的变化。在耗时方面,由于本算法在滤波交互时使用4个模型进行交互计算,使用模型数最多,因此耗时相对较长。但是本文所提算法降低了对基础模型选取的依赖性,具有更好的复杂环境适应性。
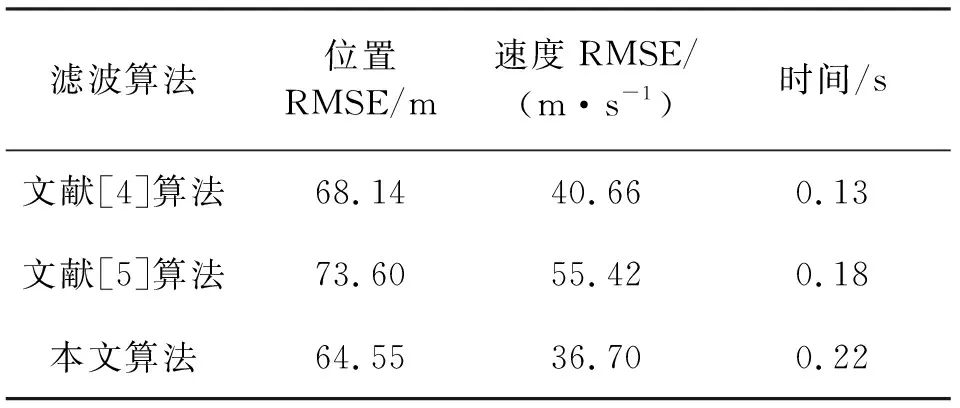
表4 算法跟踪性能对比
从图4可以看出,仿真过程中模型概率随着目标不同的机动阶段而变化:当目标作匀速直线运动时,基础模型1-大气扰动模型概率最高;当目标做大加速度机动时,基础模型3-逃避机动模型概率最高;期望模型在定角速度转弯,目标加速度偏离三个基础模型及加速度切换阶段时模型概率更高。
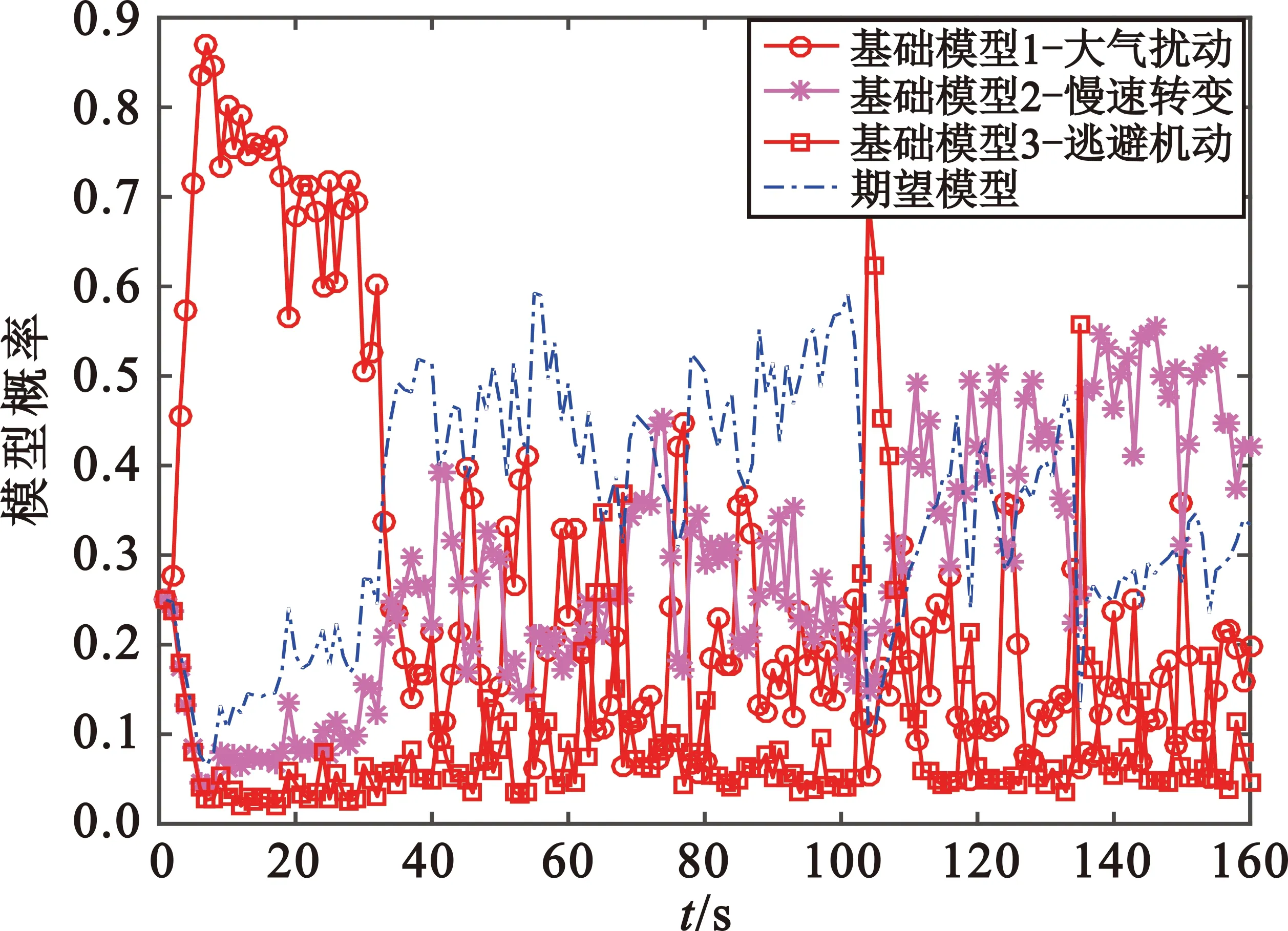
图4 模型概率随时间变换情况
4 结 论
使用固定模型算法对机动目标进行跟踪,滤波效果受所选用模型参数影响。为此,本文提出了一种基于期望模型的自适应Singer模型滤波算法。通过仿真验证,相比较文献[4]和文献[5]算法,本文所提算法滤波位置均方根误差和速度均方根误差更小,降低了滤波效果对基础模型选取的依赖性,能更好地应对机动状态与基础模型失配和目标机动状态切换的情况,因此具有更好的环境适应性。
