基于双连接和回传带宽配置的系统吞吐量效用和最大化算法*
2022-10-28张佳庚师有为锁志海
张佳庚,杜 丰,师有为,王 齐,刘 俊,锁志海
(1.西安交通大学 a.网络信息中心;b.信息与通信技术学院,西安 710054;2.国防科技大学 信息通信学院,西安 710106)
0 引 言
为了支撑不断涌现的新兴的移动通信场景,第五代(5G)移动通信系统具有网络异构化、部署密集化和业务多样化等特点。作为支撑5G的一种候选关键技术,双连接技术已经受到了学术界的广泛关注。
双连接是指用户设备可以关联至同频部署或者异频部署的一个宏基站和一个小基站,并且同时与其通信。根本上来讲,双连接是一种演进的小小区增强技术,是载波聚合技术在非理想回传网络场景下的应用实现。因此,相比传统的单关联的异构无线网络,双连接可行的异构网络结构通过提升频谱利用率来有效提升系统吞吐量,特别是系统边缘用户的吞吐量。在一个双连接可行的异构无线网络中,用户设备可以被关联至宏基站和一个小基站,实现双连接通信方式。小基站需要与宏基站通过宏基站到小基站之间的回程链路相连接,而宏基站作为服务网管实现所有用户数据与核心网之间的请求发送。因此,双连接结构的实现性能很大程度上受到回程容量的限制,特别是在宏基站和小基站同频部署的非理想回传异构无线网络中,回传带宽的配置机制将是一个至关重要的问题。
现有文献已经针对双连接可行的异构无线网络的相关问题展开了研究,比如用户关联[1-4]、带宽分配[4]、功率控制[3,5-6]和流量调度[5,7]等。但大多数现有的工作[1-3]只考虑异构网络异频部署场景,而不考虑共信道(同频)部署场景。尤其在宏基站和小基站同频部署的非理想回传异构无线网络中,关于双连接可行的用户关联与回传带宽配置的联合优化问题未见有文献展开研究。尽管文献[4]考虑了宏基站和小基站同频部署的非理想回传异构无线网络场景,但是其仅仅关注双连接可行的用户关联与前传带宽配置的联合优化问题。
针对以上考虑,本文通过联合优化用户关联和回传带宽配置,使得在满足前传容量不超过回传容量的前提下,最大化系统吞吐量效用之和。
1 系统模型
考虑一个两层异构网络的下行传输过程。该网络由一个宏基站和多个可开放接入的小基站组成,它们共同服务于在网络覆盖范围内的随机分布的用户。首先,假设所有的用户设备都有两个无线电接口,都具备同时与一个宏基站和一个小基站通信的能力。接下来,假设从小基站到宏基站之间的无线回传链路和从小基站到用户设备之间的前传链路以共信道方式部署。每一个用户设备被分配若干子信道,且假设所有信道是平稳衰落,同时每一个小基站在每一个子信道上分配相同的功率。
不失一般性,如图1所示,本文考虑由一个宏基站、M个小基站和随机分布的N个用户组成的下行异构无线网络场景。定义所有用户的集合、所有小基站的集合和所有基站的集合分别为N、M和M0。于是,以上集合可以分别被表示为N={1,2,…,N}、M={1,2,…,M}和M0={0,1,2,…,M},其中M0中元素0代表宏基站,同时存在M∪{0}=M0。

图1 双连接可行的下行两层异构网络场景图
本文采用双连接3C架构[6]。在3C架构中,所有下行数据流首先传送到宏基站,再经宏基站按照一定算法和比例进行分割后,由X2接口把部分数据发送给相应小基站,最终在宏基站和相应小基站上同时给用户设备下发数据。可见,该3C架构对宏基站和小基站之间的回程容量需求较高。
2 问题建模
小基站配置单一天线,采用单输入单输出(Single-Input Single-Output,SISO)的模式进行信号传输。而宏基站部署毫米波天线阵列,天线数为At,针对小基站的波束成形分组大小为Ag(At>>Ag)。不失一般性,假设采用正交频分多址接入机制。α定义为每个小基站的回传单位带宽配置因子,0<α<1。
假设用户设备i被关联至第j个小基站,那么其可获得的单位带宽最大用户速率可以表示为
(1)


(2)
式中:P0为第j个小基站向宏基站发送信号的发射功率,Gj为第j个小基站向宏基站发送信号的路径增益。假设用户设备i被关联至宏基站,那么其可获得的单位带宽最大用户速率Ri,0可以表示为[1]
(3)
式中:Di为宏基站向第i个用户设备发送信号的路径增益。
假设用户关联矩阵为z,z={zi,j|i∈N,j∈M0},那么zi,j存在如下定义:
(4)
本文考虑双连接可行的用户关联机制,即用户设备可以被同时关联至宏基站和某个小基站,那么可以得到关联约束如下:
(5)
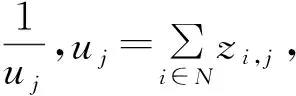
(6)
那么用户的速率约束可以写成
(7)

(8)
本文的优化目标是在考虑用户速率需求的同时,通过联合优化用户关联变量和前传带宽配置变量,最大化各个用户吞吐量效用的总和。优化问题(P1)可以建模为以下形式:
(9a)
s.t.
(9b)
式中:z={zi,j,∀i∈N,j∈M0} ,α为一个连续单一变量。在问题P1中,目标函数表示最大化用户吞吐量效用之和;C1确保每个小基站的前传容量不能超过其获得的回传容量;C2条件确保每个用户的最小需求速率得到满足;C3~C5联合确保每一个用户终端可以同时被关联至宏基站和某个小基站,实现双连接关联机制;C5和C6分别是二进制的用户关联变量约束和连续的被分配给每个小基站的单位回传带宽资源配置变量约束。

为了简化问题P1,首先考虑去除优化目标和约束条件中的分式。简化后的问题(P2)具体形式如下:
(10a)
s.t.
(10b)

转换后的问题P2依旧是一个混合整数非线性优化问题,问题的非凸性质没有发生明显变化,依旧是一个NP-hard问题。为此,采用交替优化方法将问题P2分解为两个优化子问题,即已知用户关联情况下的回传资源配置优化问题和已知回传资源配置因子情况下的用户关联优化问题。
3 问题求解
首先,在已知用户关联情况下,问题P2可以转化为一个回传资源配置优化问题(P2-1),具体形式如下:

(11a)
s.t.
(11b)
观察可知,子问题P2-1是一个连续变量凸优化问题,显然其很容易求解。通过变换,C1可以等价为
(12)
通过变换,C2可以等价为
(13)
综上,如果α1>α2,则问题P2-1无解,说明问题P2-1的基本条件即用户关联解是固定且已知的,不够合理;如果α1≤α2,P2-1问题的解为α=α1。
进而,在已知回传资源配置因子的情况下,问题P2可以转化为一个用户关联和前传资源配置联合优化问题(P2-2),具体形式如下:
(14a)
s.t.
(14b)
L(z,λ,ν,ω)=
(15)
通过移项和归类之后,拉格朗日函数进一步可以写成

(16)

(17)
(18)
(19)
式中:
(20)
(21)
对于拉格朗日乘子λ、ν和ω的更新,本文采用传统的次梯度法,过程如下:
(22)

(23)
式中:[α]+=max(α,0),ε1、ε2和ε3是三个被恰当选择的步长值。
借助式(19)和(21)获得相应的变量解,同时根据式(22)和(23)更新几个拉格朗日乘子,随着这三个乘子的更新迭代并最终收敛,至此问题P2-2就可以求解。
4 双关联和回传带宽资源配置联合优化算法
通过分别求解两个子问题得到相应的用户关联解和回传带宽分配因子,在循环内依次更新这两个变量值,最终当函数目标值收敛或者循环触发终止次数,迭代优化结束。最终问题P1的求解算法(以下简称为JDCBA算法)总结如下:

Step2 输入初始化数据:t=1,Tmax=15,α1=0.8。
Step3 Ift≥1且t≤Tmax
Step4 已知αt,求解问题P2-2,获得二进制关联变量的解z
Step5 已知z,求解问题P2-1,获得新的回传单位带宽配置因子αt+1
Step6 if 问题P2的目标值收敛
Step7 终止循环,执行Step 12
Step8 else
Step9t=t+1
Step10 end if
Step11 end if
Step12 输出数据。
5 仿真分析
针对异构无线网络中双关联可行的用户关联和回传单位带宽资源配置联合优化问题,本节通过电脑(i9-10900K处理器、32 GB内存)安装的Matlab R2017a数学仿真验证所提算法的性能。所考虑的场景是由1个宏基站和3个小基站组成的双层异构网络的下行链路传输场景。宏基站固定部署在坐标中心位置(0,0),而小基站和所有用户设备以一种相对随机的方式分布在以(350,350)m为圆心、半径为350 m的圆盘区域中,并且任意两个小基站之间的距离大于150 m。

本小节将所提算法与两种基于固定回传单位带宽配置因子的双连接方法的性能进行比较。这两种对比方法分别简称为“DC-α1”和“DC-α2”,其中α1=0.4,α2=0.7。此外,需要强调的是,所有的仿真结果都是在超过1 000次蒙特卡洛平均中得到的。
5.1 不同用户数下性能对比
图2~4分别比较了三种关联机制在不同用户数下的系统吞吐量效用、系统吞吐量和无线回传单位带宽配置因子值,网络所有户数的最小单位带宽需求速率设置为0.01 b/s。
由图2和图3可知,与DC-α1方案和DC-α2方案相比,本文所提JDCBA方案拥有最好的网络吞吐量效用和性能,同时在网络吞吐量性能方面拥有显著的优势。
在图2中,随着网络中用户总数的逐渐增加,三种方案的网络吞吐量效用和性能呈现快速降低的趋势,同时不同方案的网络吞吐量效用和性能之间的差值变大。数值计算表明,本文所提JDCBA方案的网络吞吐量效用和性能平均比DC-α1方案和DC-α2方案的网络效用性能高出7.85%和27.70%。
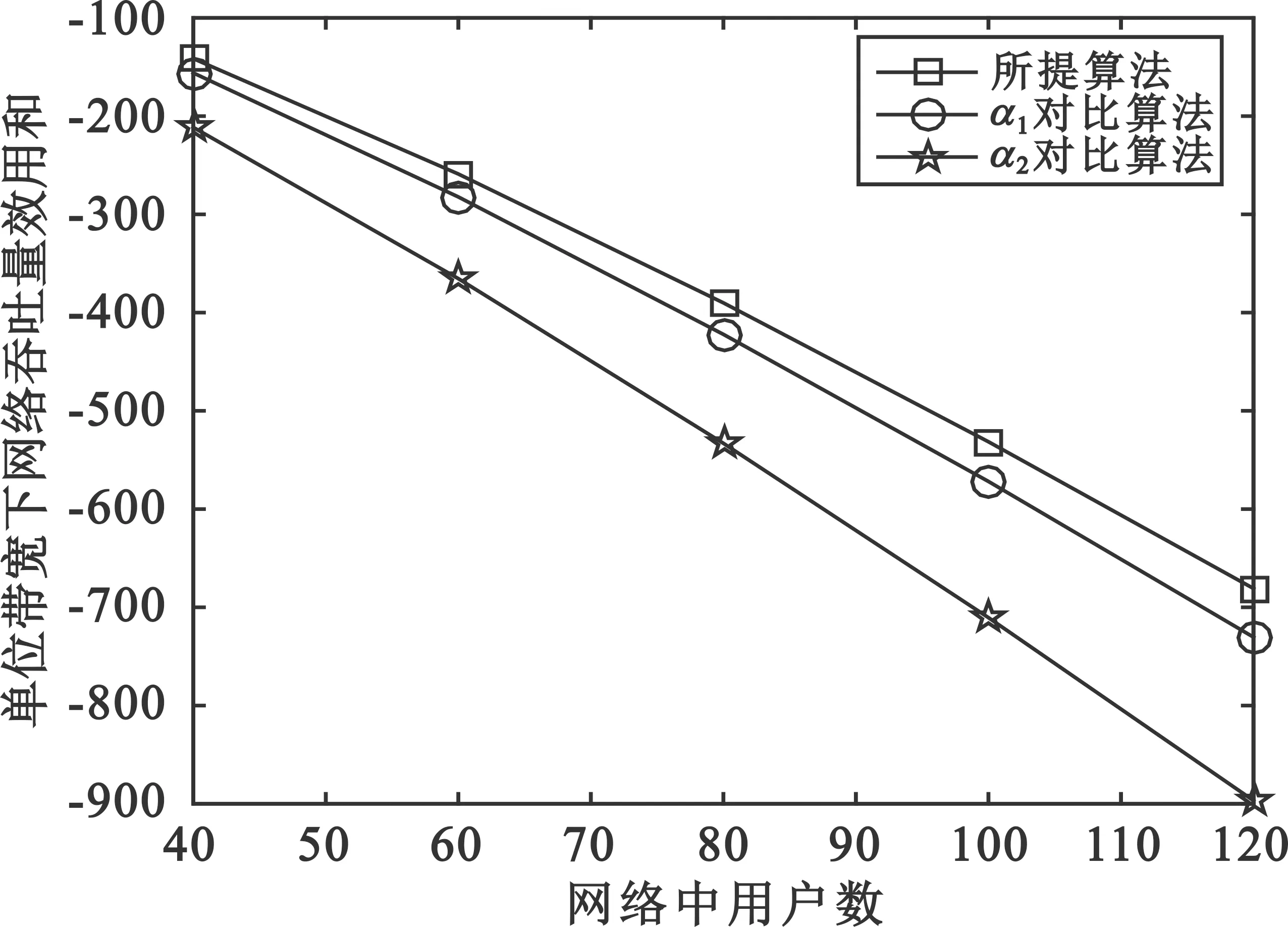
图2 不同用户数下三种机制的网络吞吐量效用和
在图3中,随着网络中用户总数的逐渐增加,本文所提JDCBA方案的网络吞吐量性能呈现缓慢增长的趋势,其他两个方案的网络吞吐量性能保持不变。数值计算表明,在网络吞吐量性能方面,本文所提JDCBA方案平均比DC-α1方案和DC-α2方案的性能分别高出22.03%和144.06%。

图3 不同用户数下三种机制的网络吞吐量
通过观察图4可知,与DC-α1方案和DC-α2方案相比,本文所提JDCBA方案拥有最小的回传单位带宽配置因子值。在图4中,随着网络中用户总数的逐渐增加,所提JDCBA方案的回传单位带宽配置因子值呈现缓慢降低的趋势。
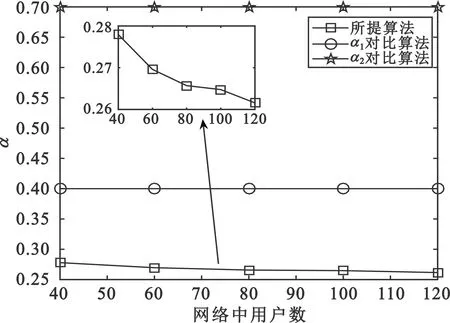
图4 不同用户数下三种机制的回传单位带宽配置因子
5.2 不同用户最小需求速率下性能对比
图5~7分别比较了三种不同关联机制在不同用户最小单位带宽速率需求下的系统吞吐量效用、系统吞吐量和无线回传单位带宽配置因子值,网络所总用户数设置为40。
由图5可知,本文所提JDCBA方案系统吞吐量效用性能最好,DC-α1方案次之,DC-α2方案最差。数值计算表明,本文所提JDCBA方案的系统吞吐量效用性能平均比DC-α1方案和DC-α2方案的系统吞吐量效用性能高出9.51%和33.21%。另外,在图5中,三条曲线呈现水平且平行的状态。这说明随着网络中用户速率需求的逐渐提高,所提 JDCBA方案和两种基于固定回传单位带宽配置因子的方案一样,三者的系统吞吐量效用和性能未发生可观察到的变化。这是因为从式(12)和(13)可知,在可行的用户速率约束条件下,网络中用户速率需求与回传单位带宽配置因子的取值无关。因此,网络中用户速率需求的变化不影响回传单位带宽配置因子的取值,这也能通过后面的图7得到验证。
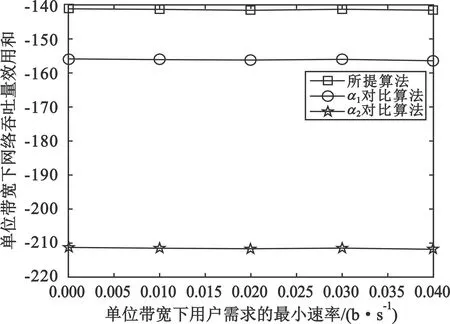
图5 不同用户最小速率需求下三种机制的网络吞吐量效用和
由图6可知,本文所提JDCBA方案系统吞吐量性能最好,DC-α1方案次之,DC-α2方案最差。数值计算表明,本文所提JDCBA方案的系统吞吐量性能平均比DC-α1方案和DC-α2方案的系统吞吐量效用性能高出20.62%和140.20%。而且,在图6中,三条曲线呈现水平且平行的状态。这说明随着网络中用户速率需求的逐渐提高,所提 JDCBA方案和两种基于固定回传单位带宽配置因子的方案一样,三者的系统吞吐量效用和性能未发生可观察到的变化。
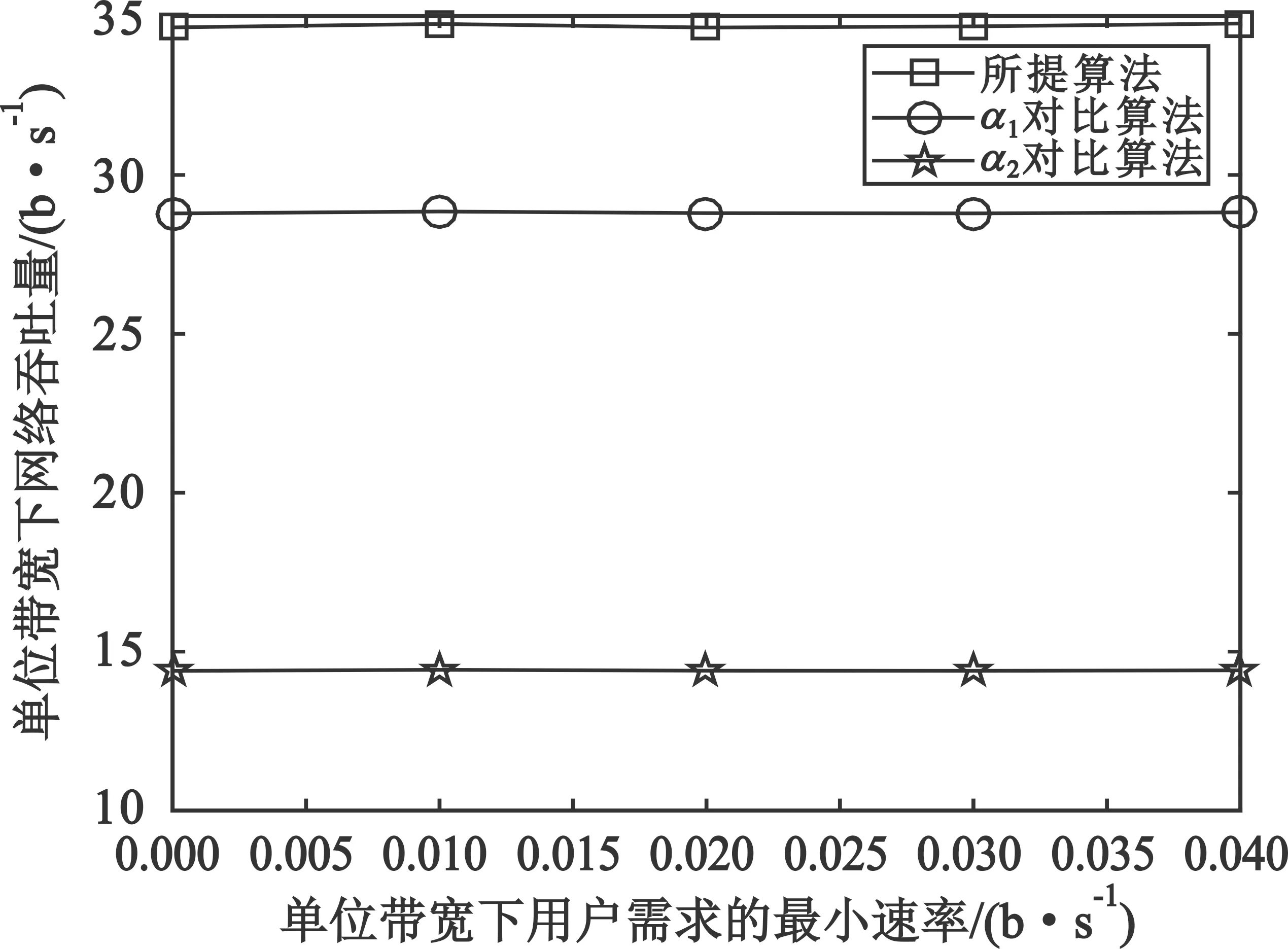
图6 不同用户最小速率需求下三种机制的网络吞吐量
图7表明,与DC-α1方案和DC-α2方案相比,本文所提JDCBA方案拥有最小的回传单位带宽配置因子值,即α值。而且,同图5和图6一样,随着网络中用户速率需求的逐渐提高,所提 JDCBA方案的α值未发生可观察到的变化。

图7 不同用户最小速率需求下三种机制的回传单位带宽配置因子
6 结 论
本文针对双连接可行的异构无线网络中基于用户关联和回传带宽配置的联合优化问题,将其建模为系统吞吐量效用和最大化问题。由于所建模问题是一个非凸的混合整数分式优化问题,属于复杂的NP-hard问题,本文首先将其去分式转换,然后进一步分解为两个优化子问题,即基于固定用户关联的回传单位带宽配置优化子问题和基于固定回传带宽配置因子的双连接可行的用户关联优化子问题。最终基于交替求解这两个子优化问题,本文提出了一种有效的迭代优化算法。数学仿真验证了所提算法的有效性和优越性。
