锯齿状泄水闸消能特性研究
2022-10-28江玫瑰
江玫瑰
(中铁十四局集团第二工程有限公司,山东 泰安 271000)
1 研究背景
泄水闸是水利枢纽中一种较为常见的泄水构筑物,当水库中的水超过境界水位时,开闸使水流通过排沙洞自由下泄。水流泄放速度过大,会对下游建筑物或大坝本身的安全构成威胁,泄放速度太小,又会降低排沙功效。因此,需要降低水流动能,将流速控制在一定范围内。金瑾等[1]采用Fluent软件,发现了紊动能及紊动耗散率的变化规律;戴光清等[2]运用三维模拟软件,修正了紊流模型系数;陈群[3]通过VOF法,建立了k-ε紊流模型,模拟出水流的水面线、流速场、压强场等;高梦露[4]通过采用Fluent软件,借助结构化网格和PISO算法,构造了两方程k-ε紊流模型和VOF模型,通过追踪自由水面线的位置,得到了锯齿状泄水闸的流速场、沿程压强变化及沿程水面线变化规律;针对消力池长度不足、泄流量高于消能防冲流量时泄槽局部出现不良水力现象,周苏芬等[5]通过模型试验,优化了溢洪道除险加固方案,实践证明消除了泄槽内水翅现象,提高了总消能率;Ohtsu I等[6]研究了锯齿状泄水闸在滑行流及跌落流两种状态下的时均压强,认为其大小随上游来流单宽流量的增大而增大;张峰等[7]结合锯齿状溢洪道水力学模型试验,引入了单宽消能功率和相对消能率的概念,总结了台阶高度与消能率之间的变化规律。
2 工程实例
昆明高海尾水泵站扩容工程位于现有高海尾水泵站北侧,西园隧洞进口明渠段南侧,呈长条形布置,建造目的是为了实现各类合流水转输、削减滇池污染负荷、保障湖体水质。为便于泵站出水,须在西园隧洞喇叭口段新建一座闸坝。坝顶高程1 888.0 m,最大坝高5 m,坝顶长度36 m,中部设置泄水建筑物,由2孔泄水闸组成,闸孔设平板工作门一道,孔口尺寸7.5 m×4 m(宽×高),闸门上方设置启闭机室用于控制闸门启闭。泄水闸示意如图1所示。

3 锯齿状消能工数学模型
3.1 控制方程
本文采用Fluent软件中的标准k-ε紊流模型进行数值模拟计算[8],其基本控制方程如下。
连续方程:
(1)
动量方程:
(2)
k方程:
(3)
ε方程:
(4)
(5)
(6)
其中,ρ为体积分数加权平均密度;t为时间;μ为体积分数进行加权平均得出的分子黏性系数;μt为湍动黏度;Gk为由于平均流速梯度引起的湍动能的产生项,σk=1.0,σε=1.3;C1ε,C2ε,Cμ均为经验常数,取值为:C1ε=1.44,C2ε=1.92,Cμ=0.09。
3.2 数值模拟设计方案
建立的数学模型分为三段,各段尺寸如表1所示,进口部位的流量设定为5档。

表1 数学模型设置
3.2.1 网格的划分
为保证计算精度,采用四面体网格划分。四面体网格适应能力较强,适合各种曲度的几何模型。由于入口处的面积相对于整个计算域非常小,对于入口附近区域需要采用加密网格,并与周围网格进行光滑过渡衔接。
3.2.2 自由面的确定
锯齿状泄水闸水流大多为暗流,但由于拱顶相对较高,因此具有自由液面,尤其对于紊流,水流水面复杂多变且形状极不规则,因此,对紊流自由液面的处理比较困难。本文采用体积率函数法,即VOF法[9]对自由液面进行追踪。
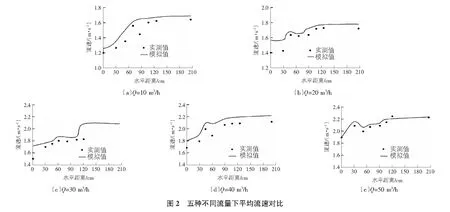
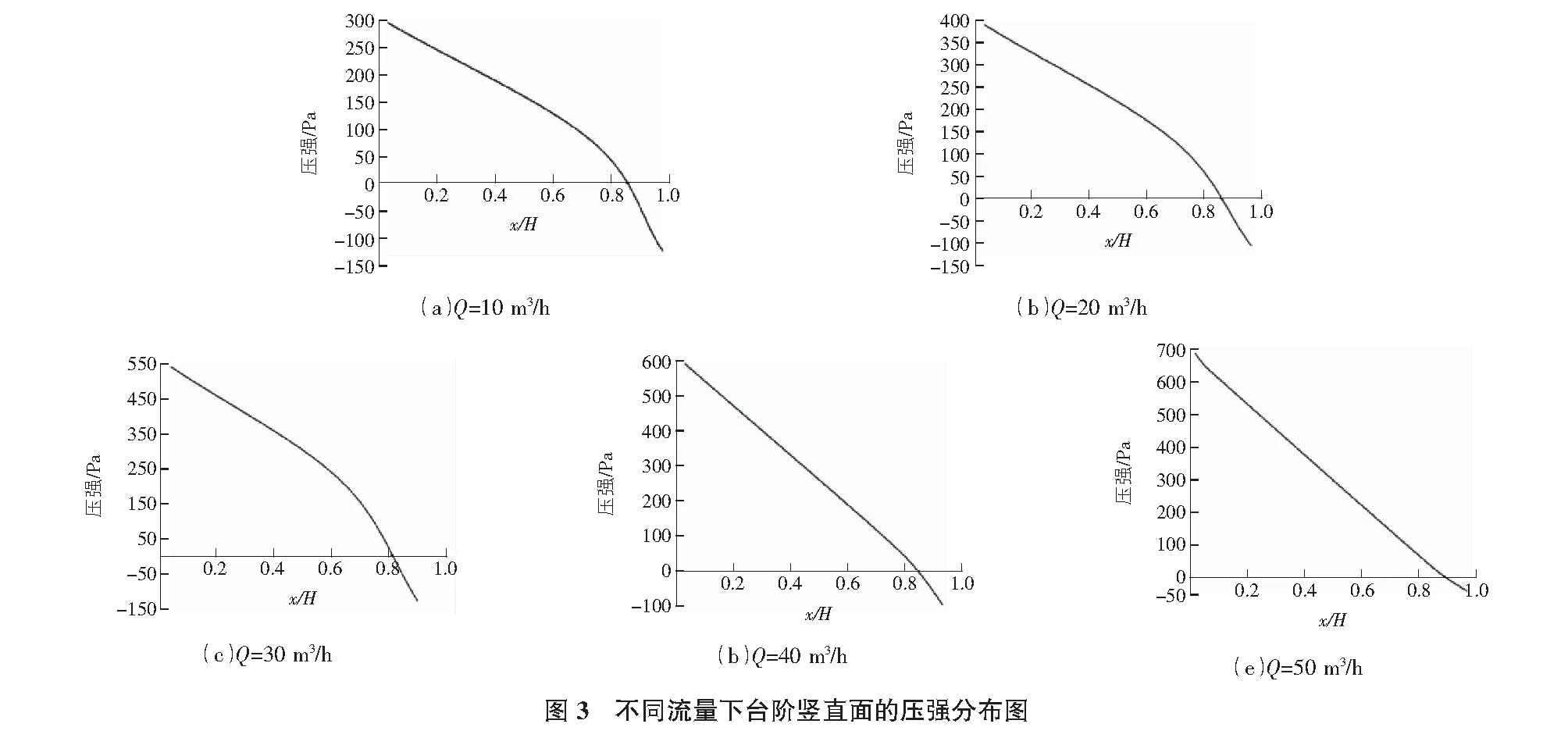
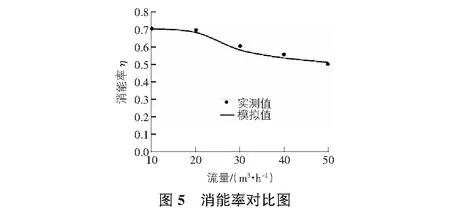
VOF法由Hirt和Nichols于1975年提出,引入变量体积分数这一概念[10],用其体积分数确定流体的自由表面位置,适合于两种或两种以上没有互相渗透的流体。VOF法中,为计算区域内某相体积和区域体积的相对比例,同时为确定自由表面,引入了体积函数F(x,y,z,t),它通过坐标及时间表示。若F=1,表示该区域充满了该相流体;若F=0,表示该区域不含该相流体;若0 (7) 其中,αw为计算域的体积分数;t为时间;μt为速度分量;xw为坐标分量。 VOF方法的优点为计算精确度高,计算效率高,所占内存少,所以成为两相流流体模拟中处理自由液面的常用方法。 将模拟得到流速值与实测流速值对比,得出五种不同流量下的平均流速对比如图2所示。由图2可知,模拟流速值与实测流速值较接近,最大相对误差约为10%,整体吻合良好,说明用Fluent软件模拟泄水闸锯齿状消能工消能特性是可行的。此外,还可看出,水流从第一个断面流出后,流速逐渐增大,再略减小,最后趋于稳定,这与物理试验观察到的现象相一致。 台阶竖直面的模拟压强分布如图3所示,由于工况较多,每种工况下又有六个台阶,每个台阶的竖直面压强分布规律相似,选取其中一个台阶进行分析,本文选择流量为50 m3/h时第三级台阶上的竖直面进行分析,横坐标为台阶竖直面某处位置,x为某一位置台阶高度,H为台阶总高度。由图3可知,在台阶竖直面上,底部压强最大,自下至上逐渐减小,约在台阶竖直高度的80%处出现负压,是由于此处的漩涡水流和壁面出现分离所致。同时还可看出,随着流量的增大,同一台阶竖直面上最大正压值增大,最大负压值减小。 锯齿状泄水闸的水面线沿程分布规律可以通过自由水面线高度来反映,模拟值与实测数值对比如图4所示。 由图4可知,两者吻合度较高,最大误差不超过10%,前三个台阶比后三个台阶的一致性更强,流量一定时,水流由台阶前的水平段进入第一级台阶后,锯齿状泄水闸的自由水面先略有升高又逐渐降低,泄水闸台阶段水流的自由表面和泄水闸的坡度基本平行;在最后一级台阶以后的水平段,水跃导致水流翻滚,掺入大量空气,导致泄水闸水深增加;不同流量时,台阶后水平段的水深高低与上游流量的大小成正比。 模拟与实测得到的锯齿状泄水闸的消能率对比如图5所示。可以看出,实测值与模拟值的最大相对误差不超过8%,表明二者吻合度较好。同时可知,模拟和实测得到的锯齿状泄水闸的消能率都随着流量增大而降低。由图5可知,锯齿状泄水闸的消能率随流量的增大而减小,最大可达70%,表明其消能效率远远大于传统光滑泄洪洞的消能率。 采用数值模拟,对泄水闸锯齿状消能工的消能特性进行了研究,得出如下结论: 1)锯齿状泄水闸的流速在垂直水流和顺水流两个方向呈现一定规律:垂直水流方向,流速自上至下逐渐减小,且其变化规律与光滑泄水闸不完全一致;顺水流方向,沿程流速先增大后减小,最后趋于稳定;两个台阶形成的三角区域之间会产生漩涡,漩涡成顺时针流动(在南半球可能成逆时针流动),漩涡自中心向外流速逐渐增大,流速从台阶的外侧向隅角逐渐减小,说明台阶隅角内发生能量损失。 2)水面线在台阶的首端均呈现“先降后升”的趋势,最后趋于稳定,但整体上沿程起伏,流量越大,水面线起伏越剧烈;同一流量下,后三个台阶较前三个台阶的水面线起伏更明显;台阶段的末端湍动能达到最大,其紊动强度也达到最大。4 锯齿状泄水闸的流速场
5 锯齿状泄水闸的压强场
6 水面线的沿程分布

7 消能效率对比
8 结论
