岩质边坡有限元强度折减法的应用研究

多仁杰

(中国核电工程有限公司，北京 100080)

边坡工程的设计和施工的前提便是边坡稳定性分析。有限元法考虑了土体和边坡形状的非线性关系，能够模拟边坡破坏过程，并能提供应力与应变的全部信息，适用于边坡的设计和监测[1]。与极限平衡法相比，有限元等数值模拟方法不需假设滑面的位置和形状，可直接获取边坡潜在滑移面，并利用边坡上特定位置处的位移突变点作为边坡失稳标志[2-3]。但现行的有限元方法很难模拟节理发育的大规模岩体中的多个节理组；在地质条件复杂的大规模岩体中，此方法也没有考虑到岩体水平方向上的非均质性。这些局限性可能会导致使用有限元方法对整个岩体的受力状态和失稳形式的分析和描述不准确[4]。

1 理论基础及模型建立

1.1 有限元强度折减法

使用强度折减法计算岩质边坡的安全系数时，取边坡刚刚好达到临界破坏状态下，对坡体的强度参数进行折减的程度，即为岩质边坡的安全系数。边坡稳定性的强度参数取黏结力c和内摩擦角φ。将坡体的初始黏结力c0和内摩擦角φ0同时除以同一折减系数K，进行数值分析。不断增大折减系数K，并反复循环直到坡体达到临界破坏状态[5-6]。假定此时的黏聚力和内摩擦角为ccr和φcr。因为此时的坡体处于临界破坏状态，对应的安全系数为Kcr=1，故初始边坡的安全系数为：

ccr=c0/F；φcr=arctan(tanφ0/F)。

其中，ccr为折减后的黏聚力；φcr为折减后的内摩擦角；F为折减系数，边坡刚刚好达到临界破坏状态下，将坡体的初始黏结力c0和内摩擦角φ0同时除以同一折减系数K，进行数值分析，直至坡体达到临界破坏状态，对坡体的强度参数进行折减的程度，即为岩质边坡的安全系数。

1.2 模型建立及参数选取

在建立边坡几何模型时，边坡考虑弹性和塑性两种材料，选取的岩体材料均为弹塑性材料。边坡上部为弹塑性的岩体1，边坡下部分是弹性材料岩体2，模型示意图见图1，其强度参数详见表1[7]。

表1 边坡模型中岩体的强度参数

随着强度折减系数F的增大，塑性应变和塑性区从无到有，并逐渐增大；当强度折减系数F=3.0时，计算的解不收敛，而且塑性区贯通到坡顶，说明此时的边坡已发生失稳破坏。故此边坡坡体的安全系数应取2.8～3.0，大致可取2.9。

2 不同影响因素对计算精度的影响

2.1 黏聚力

上述的边坡模型稳定性系数求解过程中，将围岩1的弹塑性岩质材料黏聚力假定为0.96 MPa。将围岩1的弹塑性岩质材料黏聚力假定两种方法求解的稳定性系数如表2所示。

表2 围岩1的不同黏聚力下两种方法求解安全系数

不论通过什么方法计算边坡稳定性系数，岩质边坡的稳定性系数都与其围岩材料黏聚力大小几乎成正比关系，即在一定的范围内，坡体材料的黏聚力越大，边坡的坡体结构越稳定，安全系数也就越高；而通过有限元强度折减法和极限平衡法计算求得的稳定性系数相差无几。材料黏聚力对坡体稳定性影响较大，有限元强度折减法在不同黏聚力状态下的计算精度有很高的适用性。

2.2 内摩擦角

在使用有限元强度折减法对于边坡稳定性安全系数的求解过程中，将主要坡体围岩1的内摩擦角φ假定为40°。控制其他条件不变，选取围岩1的内摩擦角和两种方法求解结果见表3。

表3 不同内摩擦角下，两种方法求解安全系数

不论坡内材料的内摩擦角的大小，有限元强度折减法的稳定性系数求解结果与传统的极限平衡法得出的结果均相似；两种结果的求解结果都能说明，岩体材料的内摩擦角越大，岩质边坡的稳定性一般也就越大；当坡内材料的内摩擦角极小时，两种方法求得的安全系数略有差距。有限元强度折减法对于不同的内摩擦角的材料组成的边坡具有一定的精度和适用性。

3 含不同结构面的岩质边坡

3.1 水平结构面

在含水平结构面的节理岩质边坡中，坡体的结构面的倾角一般很小，产状近于水平。水平结构面的岩质边坡一般稳定性较好，没有外部作用的条件下，此类边坡一般不会发生失稳破坏。显而易见的是，若在此类边坡中只进行对于结构面中内摩擦角和黏聚力进行折减时，边坡几乎不会发生明显变化，求解的稳定性系数很大，因此只对岩体材料强度折减和两者共同折减的情况进行分析对比[8-9]。

3.1.1 模型建立及强度参数选取

岩质边坡模型中加入一组间距为5 m，宽度为1 cm的结构面(如图2所示)，强度参数如表4所示。

表4 结构面材料物理参数

3.1.2 结果分析

图3为仅对岩质边坡上部岩体材料进行强度折减，折减系数达到F=2.8时，含有水平结构面的边坡模型的塑性应变云图。此时边坡安全系数可取2.7。由图3中的塑性贯通区可得此时的滑动面为类似圆弧面。

图4为对岩质边坡上部岩体材料和结构面进行同系数强度折减，折减系数达到F=2.8时，含有水平结构面的边坡模型的塑性应变云图。此时边坡安全系数可取2.7。由图4中的塑性贯通区可得此时的滑动面为类似圆弧面。

在使用有限元强度折减法进行含有水平结构面的岩质边坡的稳定性分析时，对于岩质边坡的岩质材料折减和对于结构面和岩体共同折减的两种情况的滑动面位置和形状相近，安全系数近似。且二者的变形破坏的极限状态均与含有水平结构面的岩质边坡的真实破坏形态一致。两种折减方式均能达到预想结果。在实际使用时，可以具体分析，为达到更好的安全性系数分析效果，建议采用对于两者共同折减的方法，以便在工程实际中找到潜在破坏面并对其采取相应支护措施。

3.2 顺倾结构面

在含顺层结构面的岩质边坡中，坡体内结构面的倾向与坡面的倾向相同。坡面一般也是结构面中的一个。此种坡体上，滑动体没有下滑空间。在没有开挖或爆破的情况下，边坡不会发生失稳破坏。破坏形式一般是沿结构面的岩层的弯曲破坏。在结构面倾角小于坡面倾角时，由于倾角较小，岩层具有滑出的空间。故此类坡面安全系数较低。

从上述民间武术拳种的继承者——民间武术家们对上代宗师的技艺传承来看，武术套路成为其把玩身体的工具，在精神上，他们没有全部投入武术的发展中；表面上他们被关注，实际上仍不被重视而处于底层，这就是民间武术的现实也是民间武术家的现状。作为民间武术家中的流浪者，他们为生计四处奔波，看似可以四处流动，却无法逃离穷困潦倒的现实，武术在他们手中并没有成为产品而发挥出应有的意义[11]。

3.2.1 倾角与坡面相同的顺倾结构面

边坡模型增加一组顺层的结构面倾角与坡体的相同(如图5所示)。结构面及岩体的强度参数与前文模型相同。在此模型中，若仅对结构面进行强度折减，显然所得的结果与预期中此类边坡的沿结构面的岩层弯曲破坏不同，故只考虑仅对岩体进行强度折减和对两者折减两种情况。

由图6,图7可知，在使用有限元强度折减法分析结构面倾角与坡面相同的含顺倾结构面的边坡的稳定性时，若进行结构面的折减，则显示的安全系数偏低，且变形形式不是含顺层结构面的岩质边坡的固定破坏形式。而在仅进行结构面强度折减时，模型的塑性应变云图很好的反映了此类边坡的破坏形式。

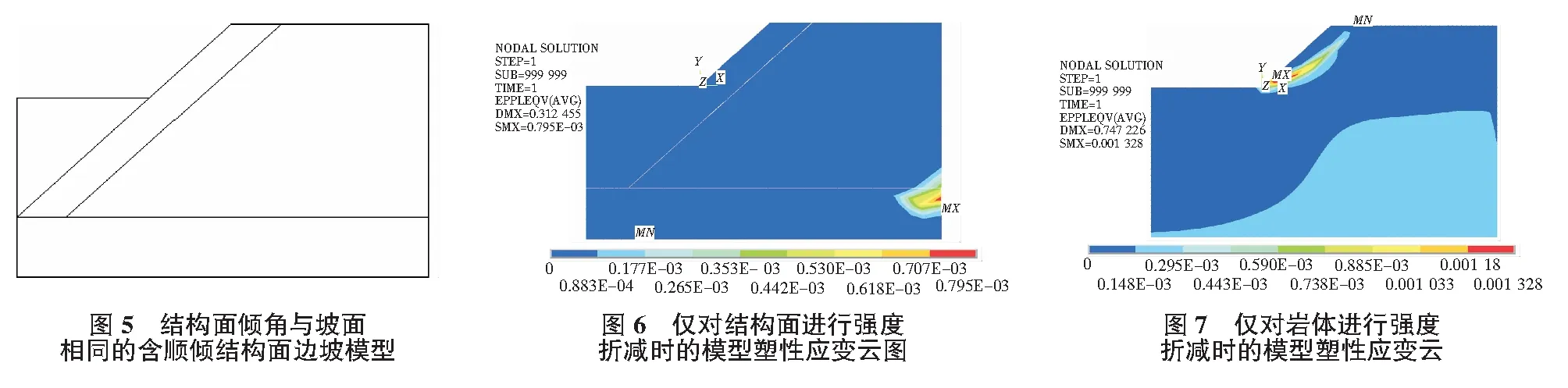
因此在分析此类边坡的稳定性时，一般不能考虑结构面强度的折减。仅考虑岩质材料的强度参数的折减。

3.2.2 倾角小于坡面的顺倾结构面

边坡模型增加一组顺层的倾角小于坡体的结构面(如图8所示)。结构面及岩体的强度参数与前文模型相同。

由图9,图10可知，在结构面倾角小于坡面的顺倾结构面的岩质边坡中，仅对岩体材料折减时得到的安全系数较大，且变形形式与预期不同。而仅对结构面进行强度折减得到结果安全系数太低，不符合实际情况。故使用有限元强度折减法分析此类边坡时，只能采用将结构面和岩体材料强度共同折减的方法。

3.3 含反倾结构面的岩质边坡

边坡模型增加一组倾向与坡面倾向相反的结构面(如图11所示)。结构面及岩体的强度参数与前文模型相同。

图12是将岩体材料和结构面两者的强度参数共同折减到F=2.8时的岩质边坡模型达到极限状态后，坡体内出现贯通面的塑性应变云图。此时的模型破坏面下部接近圆弧面，上部分向右偏移，比较符合反倾结构面的节理边坡真实情况下的倾倒破坏的变形情况。而其他两种折减方式不能得到以上效果。

仅对结构面折减时，折减系数增大而未出现贯通面，求解结果过大不合实际；仅对岩体剪切时，坡体模型破坏面不符合实际情况下的反倾结构面节理边坡破坏情况。使用有限元强度折减法分析含有反倾结构面的节理边坡时，应采用将二者共同折减求解安全系数的办法。

4 结论

1)在使用控制变量法进行不同因素下安全系数的求解精度分析时，可以得知：对于坡体内材料的黏聚力和内摩擦角，需进行周密的勘察和分析，并对其着重考虑。

2)对于结构复杂的节理边坡，坡体内部结构面与坡面的位置关系对于坡体稳定影响很大。而在使用有限元强度折减法分析节理岩质边坡的稳定性时，结构面与坡面的位置关系不同，分析方法和折减对象也不尽相同：含水平结构面的岩质边坡，折减对象应为岩体或对岩体材料和结构面材料共同折减；含反倾结构面的节理边坡的折减对象仅仅是岩体；结构面与坡面平行的顺倾节理边坡的折减对象应仅为岩体材料；结构面倾角较小的顺倾节理边坡的折减对象应为岩体材料和结构体材料两者。