新型钢管混凝土节点刚性的规律研究

苗 青

(安徽清石建筑设计研究院有限责任公司,安徽 合肥 230041)

1 概述

钢管混凝土是将混凝土填入薄壁圆形钢管内而形成的组合结构，钢管内的混凝土具有三向受压混凝土的特点，在混凝土承受轴向压力下，同时还有侧压力，混凝土裂缝的发展受到钢管的限制。钢管壁借助内填混凝土的支撑作用，增强钢管壁的几何稳定性，改变空钢管的失稳模态，从而提高其承载能力。两种材料取长补短，充分发挥了混凝土抗压性能和钢材的抗拉性能，达到优化组合的作用效果。

由于钢管混凝土的结构优点，在工程中得到了广泛的应用，钢管混凝土的节点的形式也呈现多元化，但在研究和应用中还存在一系列的问题，归结为以下几点：

1)节点不宜进行标准化、装配化。在现场施工中为了确保节点的刚性，在现场需要进行大量的焊接工作，对工人的技术水平要求较高，且节点的力学性能不能得到有效的保证。2)节点研究缺乏系统性和连贯性，节点的设计还缺乏一整套系统的理论研究做支撑。目前钢管混凝土节点的研究已经取得了不少的成果，但研究的节点形式主要是针对某一具体工程而言的，缺乏通用性，不利于其应用推广。国内如汕头大学、哈尔滨工业大学等对钢管混凝土的研究较多，进行了大量的实验，但研究对象普遍集中在常用的加强环梁节点，对其他节点形式研究较少。3)对整体钢管混凝土结构的动力学性能研究较少。从现有的研究资料来看，节点的静力性能研究得较多，动力试验研究较少；节点研究多，整体结构研究少。主要是因为动力实验对设备要求较高，且实验的过程比较复杂；相对于单个的节点，结构整体实验研究比较困难，受到场地和设备的影响。

2 新型钢管混凝土节点样式介绍

文献[1]提出了一种新型的钢管混凝土节点形式，型钢直接穿过钢管壁，连接处在工厂焊接完成，如图1所示。

该节点采用型钢穿过钢管，在节点核心区域形成穿心牛腿式节点，穿心牛腿能有效地将力传递到核心混凝土。在钢筋混凝土梁的端头预先埋置与穿心构件相同尺寸的型钢，型钢的部分伸出梁外，梁的纵筋焊接在预埋型钢的翼缘上，由此可以完成混凝土梁的工厂预制，实现了节点制作的标准化和装配化。

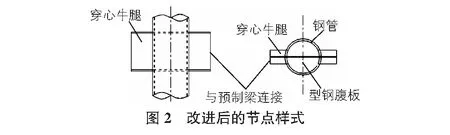
但是这种节点在实际应用中同样存在缺点。对于此新型节点，由于穿心型钢会占用钢管内空间，给钢管内混凝土的浇筑造成了困难。在节点的制作过程中，在框架的中节点，梁柱交汇的地方，由于钢管直径限制，给焊接工作带来了一定的困难，有鉴于此，对该种节点进行形式的改进，切掉钢管内型钢的翼缘，如图2所示。切除了钢管内型钢的翼缘后，在进行节点的制作时，在双梁交接的地方，焊接时，只需焊接腹板处，相对于原有节点，焊接的难度降低，由于切除了型钢的翼缘，在进行钢管内混凝土浇筑时，有利于进行混凝土的振捣，性能更好[2-4]。

文献[5]分别建立原有节点样式和改进节点样式的有限元模型，并根据文献[1]的材料常数测定数据，确定有限元模型的相关材料特性。分析两种模型的柱顶承载力，梁端承载力和节点抗震性能，对比计算分析数据可知改进后的节点相较于原有节点的柱顶极限荷载变化不大，在达到极限荷载之后下降段平缓，延性较好，两节点的滞回曲线都很饱满，具有良好的耗能能力，改进后的节点结构性能并没有明显的下降，说明节点改进具有可行性。

3 节点域参数对节点刚性的影响规律研究

节点的样式是各不相同的，因此当节点的尺寸改变时，节点的刚度如何变化就是一个值得探讨的问题。对于这种新型的钢管混凝土节点，在不同的结构中与该结构梁柱刚度具有不同的比值，则其在不同的结构中就体现为不同的刚性，在考察节点的刚性时要同时考虑钢管混凝土柱的刚度、型钢的刚度及钢筋混凝土梁的刚度。由于不同的钢材其弹性模量相差很小，因而不作考虑;在进行非线性分析时，混凝土材料的真实应力-应变曲线要通过实验获得，它的对错与否还无法下定论，因而在下面的分析中也不把它作为考虑的参数。在下面的分析中主要是从节点的细部几何尺寸方面进行分析，其主要影响因素有：1)钢管混凝土柱的半径；2)钢管壁厚度；3)腹板厚度；4)型钢高度；5)钢筋混凝土梁高度；6)钢筋直径。下面以第三节中的节点的实体模型做基础，施加梁端单调荷载，得到节点的弯矩-转角曲线，然后通过改变节点的细部尺寸做一系列的有限元计算，分析节点域各参数对梁柱连接性能的影响。

3.1 节点域弯矩-转角公式拟合

建立新型钢管混凝土节点的三维模型，定义的灵敏度分析中的输入参数，即上述影响节点刚性的六个几何参数，如表1所示，荷载的初始值为30%左右的极限荷载，输出参数取梁柱相对转角。

表1 输入参数 mm

对计算结果提取梁柱的最大转角得到样本点的组成散点图，如图3所示为腹板厚度与梁柱相对转角的散点图。

运用最小二乘法原理对图3所示的数据进行拟合，得到一阶多项式Y=C0+C1X;C0,C1分别为常数项和一阶常数。分别对各变化参数和梁柱的相对转角图进行一阶多项式拟合，提取一阶参数C1，如表2所示，将表2中第一横栏中各参数与转角的相关系数值，以荷载和转角的相关系数值为标准，即以该系数定为1，其余按对其比值，计算后如表2中第二栏，将此栏系数作为各影响参数的幂次系数，得到标准参数K的表达式(1)。

表2 输入参数与输出参数相关系数表

K=TC-0.212 17D-0.003 04TW-0.330 43d-0.279 51H-0.052 941B-0.027 79

(1)

其中，TC为钢管厚度；D为钢管柱半径；TW为型钢腹板厚度；d为钢筋直径；H为型钢高度；B为钢筋混凝土梁高度。

然后用数学软件Matlab对得到的M-θ数据进行拟合，得到反映节点M-θ关系的奇次方的多项式：

θ=C1(KM)1+C2(KM)3+C3(KM)5

(2)

其中，M为梁柱连接处的弯矩值；θ为梁柱之间的相对转角；C1,C2,C3均为曲线拟合常数，C1=2.215×10-2,C2=0.287 97,C3=-3.088 9。

3.2 结果对比

以节点中钢管壁厚度为例来探讨公式的拟合效果，首先由式(1)计算得到各钢管壁厚度下标准化参数K值，如表3所示。

表3 标准化参数计算表

由式(2)计算得到钢管壁厚度为6 mm时节点的弯矩-转角数据表，如表4所示，根据表4得到节点的弯矩-转角图，见图4。

表4 节点转角拟合数据比较

从表4，图4中可以看出当节点钢管壁厚度为6 mm时，在相同弯矩作用下，模型计算得到的转角和公式计算得到的转角的最大差值百分数为-5.80%，误差在可接受的范围之内，二者的弯矩-转角图曲线发展一致，在弹性阶段，两曲线趋于重合，在塑性阶段，由公式计算得到的梁柱相对转角较模型计算得到的转角要小。节点弯矩-转角对比图见图5～图8。

从图5～图8中可以看出，由公式计算得到的弯矩-转角图和模型计算得到的弯矩-转角图曲线发展趋势基本一致，在弹性阶段，二者的基本重合，说明公式对弹性阶段的弯矩-转角的变化趋势拟合较好。在塑性阶段，由公式拟合得到的梁柱相对转角要比模型计算得到的梁柱相对转角要大，也就是说按照公式计算得到的节点刚度要比模型的实际刚度要小，但差值并不大，在钢管壁厚度为7 mm时，差值百分数最大，数值为-4.31%，完全在可接受范围之内，说明在弹塑性阶段，用拟合得到的公式计算新型钢管混凝土节点在弹塑性节点的弯矩-转角关系，可以得到比较好的结果[6-9]。

4 结论

本文分析了节点域的几何参数对节点刚性的影响规律，得到的节点的模型。通过与有限元实体模型计算结果对比，得到如下结论：1)弹性阶段模型计算的结果和公式计算得到的结果符合较好。2)在塑性阶段，拟合公式计算得到转角要比模型计算的结果要小，即公式计算得到的节点刚度要偏大一点，总体来说拟合公式对节点刚性模拟效果较好，相关成果可供工程设计参考。