直升机主轴弯矩标识的幅-相综合相关识别方法
2022-10-28黄斌根王文涛范学伟
黄斌根, 王文涛, 范学伟
中国直升机设计研究所,江西 景德镇 333001)
直升机主旋翼系统是直升机的升力系统和主操纵平台,主旋翼载荷通过主旋翼轴(以下简称“主轴”)传导至主减速器系统,再传至机身结构,主轴是主旋翼载荷主传递通道上关键的串行部件,其设计与验证的重要性不言而喻[1-2]。主轴弯矩是新研直升机飞行试验中必须测量、分析和验证的关键技术参数之一,它是主轴设计验证、优化和疲劳寿命评估的核心环节和依据,是新机研制飞行试验实时监测、安全保障的重要一环。同时,主轴弯矩可用于逆向推导主桨毂中心振动载荷,该载荷将用于全机振动响应预估、验证,以及时常发生的机体结构kΩ振动偏大问题载荷源分析,由此技术路线获得的主桨毂中心振动载荷直接来源于型号实测数据,因此其值比通过旋翼/机身气动仿真计算得到的结果更准确[3-4],价值更高。
随着现代测试传感器性能、测试方法与检验技术的发展[5-7],已经能够准确地测量所要求的主轴弯矩,获得直升机旋翼主轴上的载荷和桨毂中心的航向力、侧向力、俯仰弯矩和滚转弯矩,并可用于主轴载荷阈值实时监测与评估、主轴使用寿命评估、飞行安全控制等[8-11]。同时,由于主轴弯矩测量端点非常多,容易出现误标识现象。若发生测量标识错误,将误导结果数据与特性的分析和后续多维度应用,从而给飞行安全和新机研制带来直接的技术隐患和风险。在直升机技术发展过程中,人们发展并形成了一些测量标识真伪识别方法,这些方法一般应用于直升机启动飞行试验前。一旦启动飞行试验,这些方法在效率和有效性方面的局限性会给试验数据检验带来困难和挑战。
针对已完成预处理、有效性判断的试验测量数据,本文提出了一种基于大子样的主轴弯矩标识的幅-相综合相关识别方法,应用于直升机主轴弯矩测量标识真伪甄别,确保主轴弯矩测量数据处理与分析结果的有效性和准确性,利用某型直升机主桨轴弯矩飞行实测数据完成该方法验证。该方法为主轴弯矩测量标识真伪甄别提供了一种高效、可靠的新手段和新选择,可以解决现有识别方法存在局限性这一问题,降低识别误差,提高主轴弯矩测量标识真伪的识别精度。该方法可以推广应用于类似旋转结构件平行截面正交方向弯矩、直升机桨叶展向不同截面摆振与挥舞弯矩测量通道标识真伪的智能识别。
1 主轴弯矩测量标识真伪问题
1.1 主轴弯矩测试典型方案
直升机桨毂中心载荷、主轴截面弯矩载荷测点典型布置几何位置、标识[12]如图1(a)所示,典型的测点标识如图2所示。采用笛卡尔坐标系和右手法则,以桨毂几何中心为坐标原点,建立桨毂旋转坐标系O-XYZ,X轴正向为逆航向。图1中Fz为主轴拉力,单位为N,向上为正;Fx为航向力,单位为N,X轴正向为正;Fy为侧向力,单位为N,Y轴正向为正;Mx为滚转弯矩,单位为N·m,X轴正向为正;My为俯仰弯矩,单位为N·m,Y轴反向为正;TQ为扭矩,单位为N·m,Z轴正向为正。
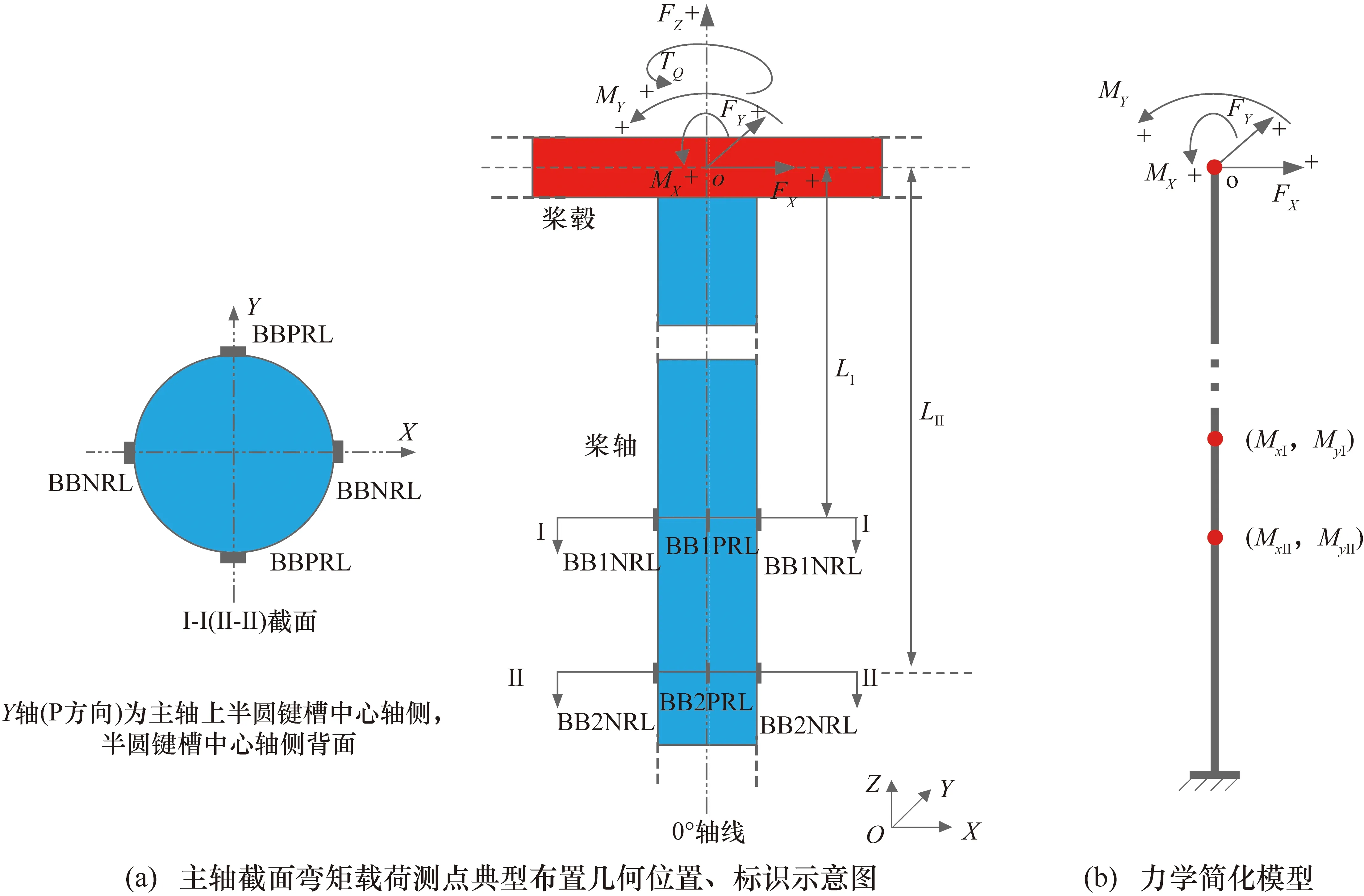
图1 直升机主轴截面弯矩载荷测点典型布置几何位置、标识及力学简化模型

图2 主轴两截面弯矩载荷测点标识及展开图
主轴截面Ⅰ与截面Ⅱ互相平行,截面内的BBNRL与BBPRL方向是正交的,如图1所示。
1.2 主轴弯矩测量标识错误及危害
在新研或重大改型直升机铁鸟或飞行试验前,须完成包含主轴弯矩测量的传感器安装、标定、校验和标识。在工程实践中,两截面与桨毂旋转中心平面的距离相差较小,导致两个截面上的弯矩MBB1NRL与MBB2NRL、MBB1PRL与MBB2PRL幅值相当,而且MBB1NRL与MBB1PRL、MBB2NRL与MBB2PRL幅值也比较接近,并且变化趋势几乎一致。上述测量标识一旦出现错误,仅从原始测试数据进行测量标识真伪勘别非常困难。
实际上,时常发生主轴弯矩测量通道标识错误,这种错误的后果非常严重,将误导主轴弯矩特性和使用寿命的评估、桨毂中心载荷的分析,这一系列的后果将误导型号设计、性能评估,甚至影响型号研制进程和成败。因此,必须对测试通道标识真伪进行精确识别,确保测试数据处理与分析结果有效、准确。
1.3 主轴截面弯矩幅-相固有特性分析
主轴根部通过轴承等组件与主减壳体连接,构成仅释放主轴转动的安装约束,根据图1所示几何关系和力学模型,建立桨毂中心处航向力Fx和力矩My、侧向力Fy和力矩Mx的计算模型:
(1)
同时,也可以得到主轴两截面Ⅰ、Ⅱ在X轴和Y轴上的弯矩MBB1NRL和MBB1PRL、MBB2NRL和MBB2PRL的计算模型:
(2)
在桨叶旋转一周的任意方位上,假设桨叶操纵量相同,则桨叶在前行方位产生的升力最大,在后行方位产生的升力最小。由此,从理论上可以定性判断,Mx稍大于My。在直升机实际飞行工况,通过施加不同的横向和纵向周期变距操纵量,实现桨盘的平衡,使得Mx与My大体相当[13-14],但由于时滞等因素,Mx、My
两者仍会存在一定的差异,这种差异可以作为识别其标识真伪的判据之一。
同时,MBB1NRL与MBB2NRL、MBB1PRL与MBB2PRL相位是一致的,存在线性强相关;而MBB1NRL与MBB1PRL、MBB2NRL与MBB2PRL相位是不相关的,以此作为勘别测量标识真伪的又一个判据。利用两个平行截面两个正交方向的弯矩的相位相关性,建立主轴两个截面4个测试通道之间的对应关系。
由式(2)可知,在桨毂旋转坐标系内,主轴任一截面的弯矩是一个矢量,其幅值和相位由桨毂中心的Mx和Fy以及该截面与桨毂中心的距离L确定。在典型水平前飞状态,Mx相对更小,MxL主要由Fy和L确定;又由于主轴弯矩两个测量截面相距不大,因此,这两个截面上的弯矩MBB1NRL与MBB2NRL、MBB1PRL与MBB2PRL幅值相当,且相位几乎一致。依据主轴弯矩的上述固有特性,可以通过分析两个截面相互正交方向的弯矩幅值和相位的相关性,对测试通道标识真伪进行准确识别。
1.4 主轴弯矩测量标识错误实例
在实际测试中,因为人为失误,会出现测试通道标识不符的错误。试验平台主轴两个截面4个弯矩(无因次化)标识错误的实例如图3所示,其中BB1NRL、BB1PRL分别是主轴截面Ⅰ在X轴和Y轴的弯矩,BB2NRL、BB2PRL分别是主轴截面Ⅱ在X轴和Y轴的弯矩。经过对各个孤立测试通道的数据进行有效性分析,可以确定各个通道的测试数据真实、有效。通过人工方法,对比实测数据曲线趋势,判断主轴两个截面弯矩测量标识出现了错误,即俗称的“标识窜道”。
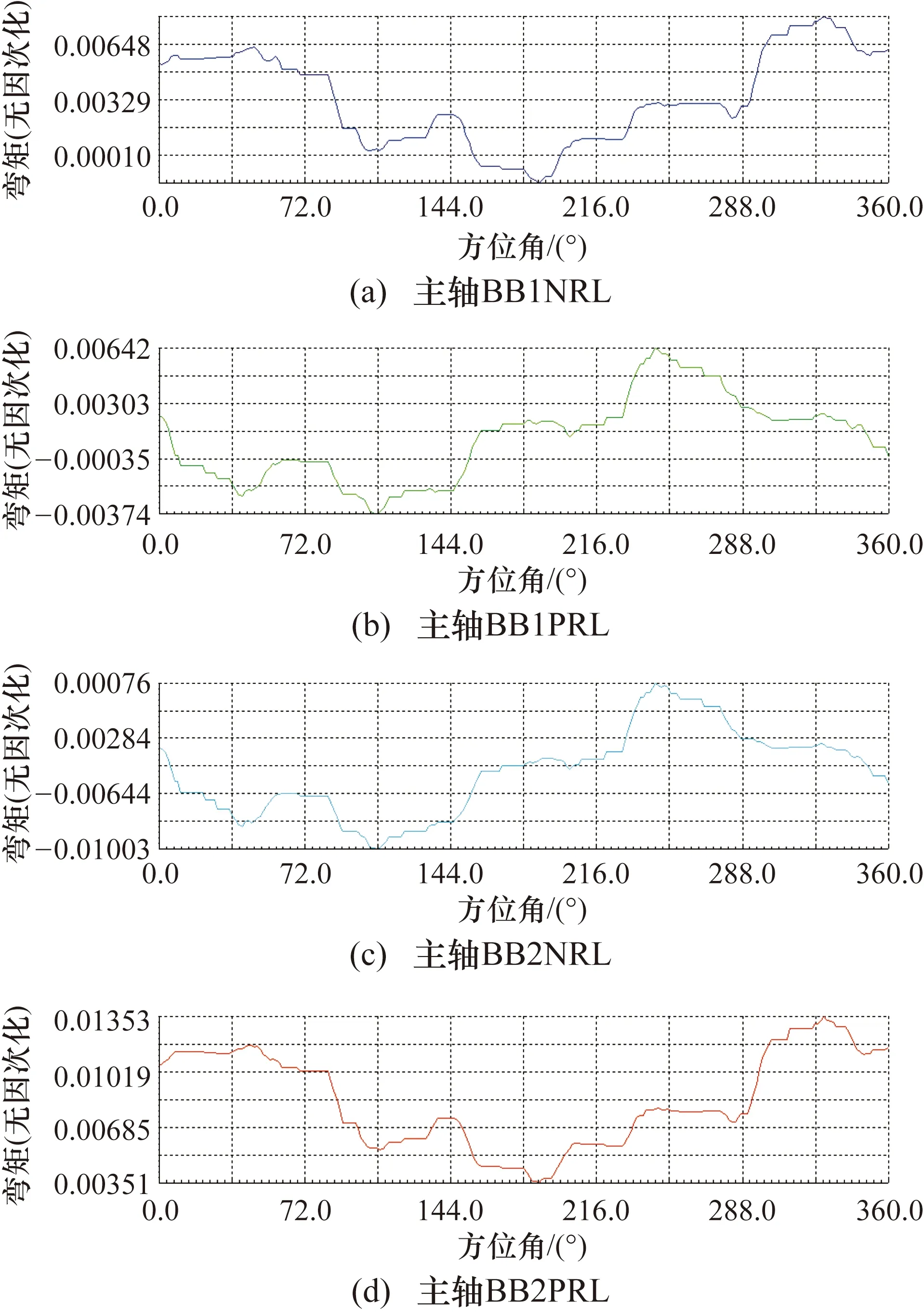
图3 试验平台某飞行架次t=1250 s起主旋翼旋转一周的时域数据
2 主轴弯矩标识幅-相综合相关识别方法
2.1 幅-相综合相关系数
首先,利用同步采集的主桨叶旋转方位角信号,对主轴弯矩信号测量信号进行谐波分析,得到每一个旋转周期内每一个测试信号的某一阶谐波分量的幅值、相位;其次,计算主轴弯矩每对测试通道每一阶谐波分量的幅值、相位的皮尔逊积矩相关系数;再分别计算每对测试通道每一阶谐波分量的幅值、相位的皮尔逊积矩相关系数的算术平均值;最后,将每对测试通道幅值皮尔逊积矩相关系数的算术平均值乘以其相位的皮尔逊积矩相关系数的算术平均值,得到幅-相综合相关系数。幅-相综合相关系数准确反映了主轴两个平行截面互相正交的方向测量通道信号的强相关性,以此作为主轴弯矩测量通道标识真伪的判据。
2.2 主桨轴弯矩实测数据谐波分析
直升机研制过程飞行试验中,为了获取有效的主轴测量试验数据,其测试传感器的采样频率一般采用1024 Hz,因此,可以有效获得旋翼转速高阶谐波分量的试验数据,这些数据是在时间域内等间距的离散量。同时,不同测试通道是同步采集的。主轴弯矩的频谱分析可以采用FFT分析方法,但是FFT分析只能获得某个频率下振动载荷的幅值,无法得到该频率振动载荷的相位。因此,需要采用谐波分析方法进行频谱分析,获取所需谐波分量的幅值和相位。
谐波分析过程如下。
① 根据旋翼转速信号,截取旋翼旋转一周的采样点数N、每个点的时域实测幅值Fj、每个点j的相对方位角Ψj。其中,N为对fc/Ω得到的商取整,fc为主轴弯矩数据信号的采样频率,Ω为旋翼工作转速。
② 对每个等分段的采样点N进行余弦和正弦的离散傅里叶变换,得到对应的谐波分量Fic和Fis,i为谐波分量阶数。
(3)
(4)
③ 计算旋转一周内第i阶谐波量的幅值Fi及其相位角Ψi。
(5)
(6)
通过上述处理,得到主轴两个截面正交方向n个旋转周期的不同谐波弯矩分量幅值Fbip。幅值下标b为测量通道,b=1,2,3,4,b=1表示截面Ⅰ-Ⅰ的R方向,b=2表示截面Ⅰ-Ⅰ的P方向,b=3表示截面Ⅱ-Ⅱ的R方向,b=4表示截面Ⅱ-Ⅱ的P方向,其中截面Ⅰ-Ⅰ与截面Ⅱ-Ⅱ平行,R方向与P方向在同一个截面内,两者正交;下标i为谐波阶数,i=1,2,…,k,k一般不超过6;下标p为所选飞行试验时间段内主轴旋转周期顺序编号,p=1,2,…,n。
同理,可以得到主轴两个截面正交方向n个旋转周期的不同谐波弯矩分量相位Ψbip。
2.3 主轴弯矩不同测量参数幅-相相关性
试验平台飞行试验受到来流非稳定、操纵扰动等诸多外界因素的影响,导致主轴弯矩的振动载荷存在较大的分散性,因此需要大子样测量结果数据进行测试通道之间的相关性分析,消除外界干扰因素的不利影响。在处理得到主轴两个截面正交方向不同谐波弯矩分量幅值和相位后,选择4个测量通道的两两测量通道(含自身)的同一阶谐波分量的幅值和相位进行相关性计算。
利用2.2节的方法,处理得到了主轴两个截面的2个方向的等间距的离散幅值和相位的结果数据Fbi和Ψbi。每组数据有n个子样,n大小由所选取飞行时间段确定。
(7)
式中,Fbip是一组等间距的幅值离散量Fbi1,Fbi2,…,Fbin。
采用皮尔逊积矩相关系数计算方法[15],计算公式为
(8)
计算得到任意两个测量标识通道结果数据的相关系数。例如:将b=1分别与b=1,2,3,4时的两组幅值离散量进行相关性计算,得到所选飞行时间段各个测量通道的各谐波分量幅值相关性系数阵列rF1bi:
(9)
同理,计算得到所选飞行时间段各个测量通道的各谐波分量相位相关性系数阵列rΨ1bi:
(10)
2.4 测量通道标识真伪识别判据

(11)
(12)
(13)
若两个测量通道的幅值、相位的相关系数不小于0.9,但小于1,由式(13)得幅-相综合相关系数,其值范围为0.81≤rFψ<1.0,则判定它们为不同截面相同方向的测量通道。若两个测量通道的幅-相综合相关系数小于0.81,则判定它们是不同截面的正交方向的测试通道。据此,建立主轴弯矩测量通道标识真伪识别判据,见表1。

表1 主轴弯矩测量通道标识真伪识别判据
将表1中的识别判据嵌入数据处理与分析工具,从而实现进行主轴弯矩测量通道标识真伪的自动识别,可以替代以往基于经验的人工识别,实现识别的智能化。
3 幅-相综合相关识别方法验证
3.1 主轴弯矩载荷结果数据
选择某型直升机平台某个飞行架次1200~3050 s时间段不同表速前飞状态的实测数据进行主轴弯矩测量标识真伪的谐波分量幅-相相关性智能识别方法验证。
测试部门给出的主轴两个截面弯矩测量通道的标识见表2。

表2 主轴两个截面弯矩测量通道标识
主轴弯矩原始测试数据的采用频率为1024 Hz,旋翼工作转速为258 r/min,原始测试数据谐波分析得到的子样数为7955。首先,对实测原始数据进行无因次化处理,得到两个截面弯矩载荷无因次化时域结果数据曲线,如图4和图5所示。从图4中很难对测试通道标识的真伪进行甄别。从图5中可以发现两个截面的测试通道相位存在明显差异,初步定性判断测量通道标识存在标识错误,但无法给出定量判别标识的真伪。

图4 不同表速前飞状态弯矩时域数据曲线

图5 典型前飞状态弯矩单秒时域数据曲线
3.2 主轴弯矩测量通道标识识别
以BB1PRL为参照测试通道,分别计算主轴两个截面4个测试通道前6阶谐波分量幅值和相位的皮尔逊相关系数及其前6阶谐波的均方根值,结果见表3和表4,两个截面4个测试通道任意两者之间的谐波幅-相综合相关系数见表5。图6、图7给出了BB1PRL标识测试通道与BB1NRL、BB2NRL两个测试通道的1阶谐波分量幅值、相位的相关性数据图。
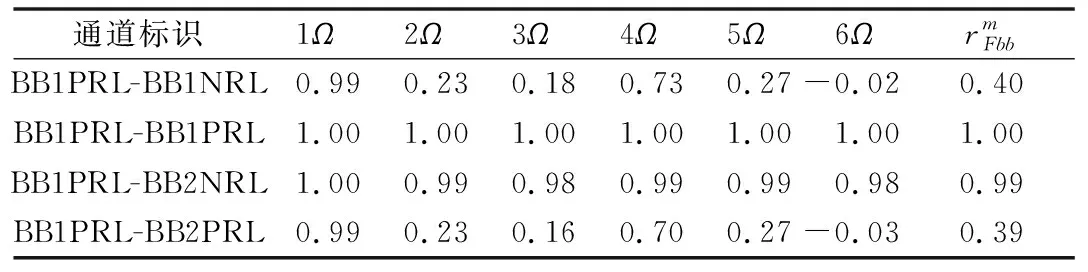
表3 主轴弯矩任意两个测试通道不同谐波分量幅值相关系数
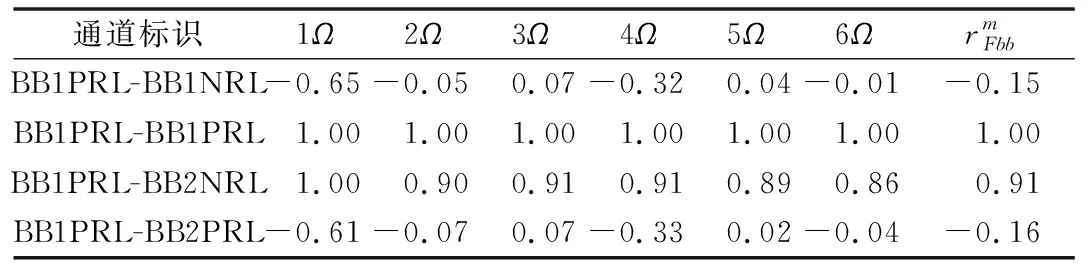
表4 主轴弯矩任意两个测试通道不同谐波分量相位相关系数

表5 主轴弯矩任意两个测试通道之间的谐波幅-相综合相关系数
表5中各个测量标识通道数据的谐波幅-相综合相关系数表明,BB1PRL与BB2PRL的rFψ为-0.06,BB1PRL与BB2NRL的rFψ为0.90,说明BB1PRL与BB2PRL标识的两个测量通道的方向不一致,而BB1PRL与BB2NRL标识的两个测量通道的方向一致。所以表2中的测量标识BB2NRL与BB2PRL是不符的,应该互换,以确保测试通道标识与实际相符,避免出现分析错误。
表3~表5与图6、图7的结果数据表明:

图7 BB1PRL与BB2NRL通道的1阶谐波分量幅值、相位的相关性数据图
① 主轴弯矩4个测量通道任意两通道的1Ω谐波分量幅值的相关系数值均比较高,而且接近1。这是由以下两个原因造成的:一是每个截面相互正交方向的载荷幅值相当,变化趋势趋同;同时,两个截面相距较小,使得两个截面同向弯矩幅值相当。二是1Ω谐波分量是主轴弯矩振动幅值的主要分量,而且占非常大的权重(贡献度)。所以,仅用时域幅值相关性容易产生误判。
② 主轴弯矩4个测量通道任意两通道的1Ω谐波分量相位的相关系数准确地反映了不同截面测量方向的差异性,相关系数接近1表示两个通道测量方向相同,否则为正交的方向。
③ 表2给出的试验平台的BB1PRL通道实际上与BB2NRL通道的测量方向相同,而不是BB2PRL通道,即BB2NRL与BB2PRL两个测量通道的标识是错误的,应该进行互换。
至此,通过主轴弯矩两个截面互相正交方向测量通道测量数据的幅-相综合相关系数计算和分析,完成主轴弯矩测试通道标识的甄别。同时,验证了上述方法的有效性和准确性。
4 结束语
直升机主轴弯矩标识的幅-相综合相关识别方法创新性提出幅-相综合相关系数这一概念,相对于数据曲线图形人工识别方法,给出了量化的具体判据,具有简单、直接、精确与智能的优点,并得到实际飞行实测数据的验证,为保障直升机型号研制试验数据处理与分析结果的有效性和准确性,提供了一种新的技术途径和工具。该方法也可以推广应用于类似旋转机械轴不同截面正交弯矩、桨叶挥舞和摆振弯矩测量通道标识真伪的精确识别。
