基于像素投票的人手全局姿态估计

林晋钢，李东年，陈成军，赵正旭

（青岛理工大学 机械与汽车工程学院，山东 青岛 266520）

1 引 言

人手姿态估计是计算机视觉领域的重要研究课题之一，广泛应用于人机交互、机器人示教学习和手势识别等领域。由于人手结构复杂、姿态多变、观察视角多样性等特点，基于计算机视觉的人手姿态估计是一项具有挑战性的任务。目前，基于视觉的人手姿态估计方法通常分为3类：生成式方法、判别式方法和混合式方法。

生成式方法［1-2］通过设计目标函数评价预先建立的人手模型与给定的人手图像的相似程度，利用某种优化算法调整人手模型姿态，实现它与人手图像的拟合，并通过缩小目标函数值，实现给定图像与人手模型的匹配。但该方法需要初始化，且存在高维状态空间搜索的难题。判别式方法［3-4］利用大量训练数据学习一个从图像特征空间到人手姿态空间的映射，无需初始化，姿态估计速度快，但其性能受到训练数据的影响。混合式方法［5-6］对生成式与判别式方法进行了融合，利用判别式方法产生初始结果，然后使用生成式方法优化初始结果。该方法利用判别式方法解决初始化的问题，基于生成式方法使用时序信息与空间信息约束来平滑预测结果。

近年来，卷积神经网络（Convolutional Neural Network，CNN）已经广泛应用于三维人手姿态估计领域。基于CNN 的人手姿态估计方法通常分为两类：全局回归法［7-10］和局部检测法［11-15］。全局回归法通常利用深度CNN 提取图像特征，再利用全连接层回归人手姿态参数，但是全连接层全局特征聚合的操作，不能很好地利用局部空间上下文信息。局部检测法精度较高，通常利用编码器-解码器的结构为每个关节生成位置热图，但解码器通常使用计算速度缓慢的反卷积操作，而且编码器-解码器结构通常利用不可学习的后处理方法实现从位置热图到关节坐标的推断。

Sharp 等［16］通过建立决策丛林来构造一个两层人手姿态初始估计模块。两层姿态初始估计模块通过两阶段来对人手姿态进行初始估计。第一阶段将人手全局姿态表示为128 个离散姿态区间，通过第一层的预测器估计人手所属的姿态区间。第二层为每个姿态区间独立训练预测器，该预测器在第一层预测结果的基础上细化回归人手的全局姿态。但该方法仅为混合式方法提供粗糙的初始结果，所预测的人手全局姿态精度较差。Liang 等［17］提出具有优化叶子节点的霍夫森林进行人手全局姿态估计，通过学习叶子节点中的投票权重以抑制错误投票对预测结果的影响，但该方法依赖于人工制作的复杂学习特征。基于CNN 的人手姿态估计方法，大多数侧重于全自由度手部姿态估计任务。因此，这些方法在变化的手势下对人手进行全局姿态估计的准确性，不能满足需要精确旋转控制的人机交互应用［17］。在人手直接参与的人机交互场景中，手部旋转是常见的交互动作，例如在抓取虚拟物体的应用场景中，操作者利用抓握动作完成对虚拟物体的抓取，抓取完成后旋转手部用以调整对虚拟物体的观察视角。在实际应用场景中，可以通过组合使用手势识别与手部全局姿态变化识别来实现复杂的人机交互动作。一些研究者采用CNN 来进行人体头部全局姿态估计。Ruiz 等［18］提出一种基于多损失深度CNN 的人体头部全局姿态估计方法，通过结合分类方法和回归方法优势来提升全局姿态估计的准确率。Yang 等［19］提出一种基于回归与特征聚合的人体头部全局姿态估计方法，采用分段软回归的方法解决了直接回归全局姿态误差较大的问题。这些全局姿态估计方法针对近似刚体的人体头部，并不能为手势多变的人手提供准确的全局姿态预测。因此，手部全局姿态的估计是十分有意义的。

深度相机成像包含距离信息，具有不受光照条件、背景色彩限制等优势，因此被广泛应用于人手姿态估计领域。根据相机成像方式，深度相机可分为结构光与飞行时间（Time of Flight，TOF）两类［20］。其中，以Kinect V2 为代表的基于TOF 的消费级深度相机，能够以低成本获取准确的深度图像。基于TOF 的深度相机原理是首先通过相机发射光脉冲至观测物体，然后相机接收从观测物体反射的光脉冲，最后通过光脉冲飞行往返时间计算二者之间的距离。利用深度图像求解人手姿态能够有效避免二维图像的歧义性问题。同时，可通过深度图像获取手部到相机的物理距离。利用距离信息可将人手与复杂背景分离，避免杂乱背景信息的干扰。

人手全局姿态估计旨在通过输入图像估计3D 手部的旋转角度，与之相似的问题还有3D 头部姿态估计。值得注意的是，头部可以近似为刚体，且因为人体生理约束限制，头部旋转范围较小；但手部运动范围大，且手势多变，相比之下手部全局姿态估计任务更具有挑战性。在数据集方面，规模大、标记精度高的数据集是保证CNN能够进行有效训练的基础，但现有人手姿态数据集大多采用人手关节3D 位置标签，缺少人手全局姿态标签，且数据集中的人手动作存在着无法完整覆盖手部动作空间的问题。

本文提出一种基于像素投票的人手全局姿态估计网络，以深度图像作为输入在变化的手势下估计手部3D 旋转角度。该方法旨在提供更高精度的旋转角度估计以满足人机交互中精确旋转控制的需求。同时，针对数据集少、动作样本难以覆盖整个手部运动空间的问题，本文通过三维渲染引擎OSG 建立人手数据集合成程序。该程序可实现不同手势下的人手深度图像渲染、全局姿态标注工作，为人手全局姿态估计提供大量高质量的训练数据。

2 模型构建

基于像素投票的手部全局姿态估计网络结构如图1 所示。给定一张深度图像，从图像中估计手部的全局旋转姿态θ=(θp，θr，θy)，其中，θp，θr，θy分别表示手部全局旋转的俯仰、翻滚和偏航3 个欧拉角。该网络基于编码器-解码器架构，包括两个功能分支：语义分割分支和姿态估计分支。这两个分支分别预测每个像素的语义信息和姿态投票信息。本文利用语义分割分支分割出手部像素区域，再利用手部像素姿态投票信息获得全局姿态估计。

图1 基于像素投票的人手全局姿态估计网络整体结构Fig.1 Overall structure of global hand pose estimation network based on pixel voting

2.1 编码器-解码器架构

受到DeeplabV3+［21］语义分割网络的启发，这里采用了编码器-解码器结构来获得像素级的语义分割与姿态预测。该结构包括用以提取特征信息的编码器和预测语义信息与姿态信息的解码器。

编码器由主干网络和空洞空间金字塔池化（Atrous Spacial Pyramid Pooling，ASPP）模块组成。本文采用深度残差网络ResNet101［22］作为主干网络，用于图像特征提取。ResNet101 利用跃层连接的方式有效解决了CNN 深度增加所造成的梯度消失、梯度爆炸等问题［23］，因此具有更好的学习与表达能力。ResNet101 可以利用公开数据集进行预训练，本文采用ImageNet 数据集［24］对ResNet101 进行预训练。实验证明，采用预训练主干网络的模型具有更好的图像特征提取能力，且后续训练收敛更快［25］。为使ResNet101 更适合基于像素投票的姿态估计方法，这里去除了该网络的全连接层，并将Conv_x4 输出的特征图分辨率从原有输入图像1/32 倍调整为1/16 倍，从而更好地保留空间关系；并将卷积层Conv_x4的卷积调整成扩张率为2 的扩张卷积，从而扩大CNN 的感受野。

针对手势多样性与姿态复杂性的特点，利用ASPP 模块在多个尺度上捕获上下文信息，进而增加网络提取不同手部姿态特征的能力。ASPP模块结构如图2 所示，该模块由4 个分别为1×1卷积和扩张率分别为3，6，9 的3×3 卷积组成。首先，将主干网络输出的特征图分别输入ASPP模块与全局平均池化层获得5 个通道数为256，尺度不同的特征图。然后，将获得的5 个特征图在通道维度上进行连接，生成1 个通道数为1 280的融合特征图。最后，利用1×1 卷积将融合特征图通道数从1 280 调整至256 完成编码工作。

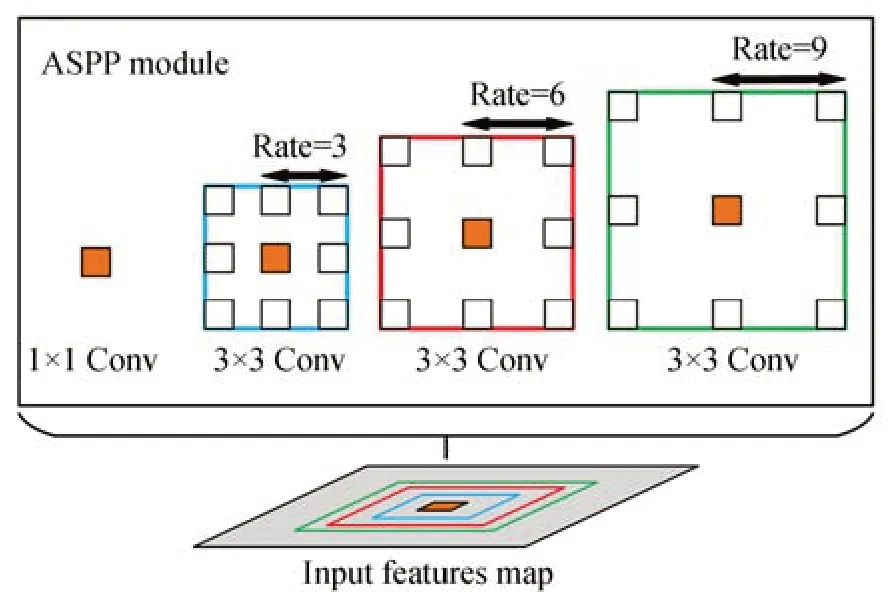
图2 ASPP 模块结构Fig.2 ASPP module structure

解码器需要将编码器得到的特征图上采样至输入图像分辨率。DeeplabV3+的解码器将得到的特征图进行4 倍双线性上采样操作，然后与主干网络中具有相同分辨率的低阶特征在通道维度上连接。连接前利用1×1 卷积调整低阶特征通道数量，避免低阶特征的大数目通道（例如256 或512）所导致的训练困难。连接后利用3×3 卷积操作进行特征提取。解码器将编码器输出的特征图进行4 倍双线性上采样操作，与特征提取主干网络中Conv_x2 层所提取的低阶特征图相连接。该低阶特征图有256 个通道，在与编码器特征图连接之前利用1×1 卷积调整至48 个通道。连接后获得304 个通道的融合特征图，利用3×3 卷积操作进行最后的特征提取。再次利用4倍双线性上采样操作得到与输入图分辨率相同的特征图。最后完成解码工作，输出包含语义信息与姿态信息的8 通道特征图。

2.2 语义分割分支

虽然利用姿态估计分支可以预测每个像素的姿态投票，并通过汇集所有像素投票的方式得到最终的姿态预测结果。但本文认为模型在进行人手全局姿态估计时需更加关注手部区域像素，因此应区分深度图像中像素的类别。为了有效汇总像素姿态投票，本文通过语义标记将图像中所有像素标注为手类或背景，在预测时通过语义分割分支获得每个像素的准确类别。

编码器-解码器模块生成的8 通道特征图同时包含语义信息与手部全局姿态信息。本文将特征图的前两个通道作为语义分割分支的输入。输入语义分割分支的特征图与原始图像的分辨率一致，特征图通道记录每个像素的语义标记分数。利用Softmax 函数计算每个像素对应各个类别的概率，即：

其中：Ki表示每个类别的语义标记分数，C为所有类别的个数。

2.3 姿态估计分支

本文目标是求解手部全局姿态θ。因为θ在3D 空间不受约束，其不同维度是不相关的，因此可以独立求解每个维度的参数。每个维度的参数由欧拉角表示，但欧拉角表示法存在不连续性，不适用于微分和积分的运算，不利于CNN 的学习［26］。为了解决上述问题，本文并不直接预测每个维度的欧拉角，而是预测其正弦值与余弦值。那么任意手部全局姿态θ可用姿态向量表示，即M=[sinθp，cosθp，sinθr，cosθr，sinθy，cosθy]。这种表示方法具有连续性，有利于CNN 学习图像特征到旋转姿态空间的特征映射。

在进行全局姿态估计时，PoseCNN［27］利用三层全连接层完成高阶特征信息到全局旋转姿态的映射。最后一层全连接层直接输出刚性物体的全局旋转姿态估计。但本文认为利用全连接层完成特征映射会破坏空间信息，不利于解决手势变化多样的手部全局姿态估计问题。所示本方法保留二维特征形式，为每个像素分配姿态标签，通过像素投票获得预测姿态。

姿态估计分支将编码器-解码器模块生成特征图的后6 个通道作为输入，每个通道对应单一维度欧拉角的正弦或余弦姿态信息。基于前文所述，在进行姿态估计时仅关注手部位置像素，所以需获得仅在手部像素保留信息的姿态标签图与特征图。姿态标签图的获取过程如图3 所示。首先，利用语义标签生成手部掩码图。然后，根据手部全局姿态生成姿态标签图。生成的姿态标签图共有6 个通道，尺寸同手部掩码图一致，每个通道记录手部全局姿态不同维度欧拉角的正弦值或余弦值。最后，利用手部掩码图屏蔽姿态标签图的背景像素，获得仅在手部区域记录姿态信息的姿态标签图。在训练时，利用手部掩码图屏蔽输入特征图的背景像素，再利用输入特征图与姿态标签图进行人手全局姿态估计损失的计算。

图3 生成姿态标签图Fig.3 Generate pose label map

本分支预测时，手部全局姿态的获取过程如图4 所示。首先，利用语义分割分支生成手部掩码图。

图4 获取手部全局姿态Fig.4 Aquisition of global hand pose

该图用以保留输入特征图的手部区域像素，以保留的手部像素作为投票像素。然后，由式（2）将所有投票像素同一通道的预测值均值作为对应通道的姿态投票结果。通过6 个通道对应的投票结果可获得预测姿态向量Mp。最后，预测姿态向量Mp通过反正切函数求解得到预测的手部全局姿态θp。本文将像素投票函数定义为：

其中：N表示手部像素的个数，pn表示每个手部像素，vi表示手部像素每个通道的姿态投票，Vi表示每个通道的姿态投票结果。

3 损失函数

本文提出的方法需执行两个任务：语义分割和姿态估计。这里使用交叉熵（Cross-Entropy）作为损失函数来训练语义分割分支。对于姿态估计分支，利用Smooth L1 损失函数（如式（3））构建像素姿态损失函数Lpp，该损失定义如式（4）所示。

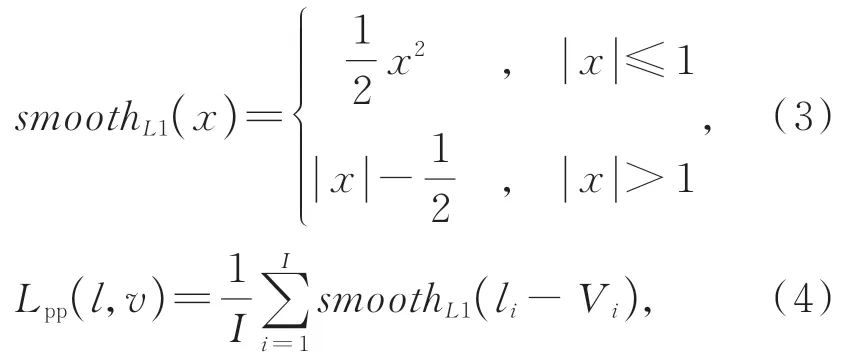
其中：I表示输入姿态特征图的通道数，li表示每个通道的真实姿态值，Vi表示手部像素每个通道的姿态投票值。

本文利用交叉熵损失函数与像素姿态损失函数共同监督基于像素投票的人手全局姿态估计网络的学习。网络损失函数为：

其中：Ls表示语义分割分支给出像素类别预测概率分布与真实像素类别概率分布之间的交叉熵；α表示平衡系数，用于平衡语义分割任务与姿态估计任务之间的关系。

4 实 验

本文方法在合成数据集上进行训练和量化评价。此外，利用Kinect V2 深度相机拍摄真实手部深度图像进行定性测试，以验证该方法在真实场景下的使用效果。实验是在拥有4 块NVIDIA TITANXP GPU，2 个型号为Intel Xeon E5-2650V4@2.2GHz CPU，128 G 内 存 的 高性能服务器上完成的。

4.1 合成数据集的制备

本文在Visual Studio 2013 编译器上，基于开源跨平台三维渲染引擎OpenSceneGraph（OSG）开发人手数据集合成程序。该程序用以生成大量手部深度图像与对应的全局姿态标签。

合成数据集的制备过程如下：首先建立场景，并在场景中加载三维人手模型，然后通过虚拟相机观测场景中不同手势不同姿态下的三维人手模型。三维人手模型的建模精度越高，越有利于获得更近似真实人手的图像数据，但是使用更高建模精度的三维人手模型进行姿态变换也意味着更高的计算复杂度。因此，需要平衡模型精度与计算复杂度之间的需求关系。人手是由多个指节与手掌铰接而成的关节式物体。根据这个特点，本文利用圆台、球体等几何基元建立三维人手模型的各个部件，控制模型中的各部件旋转运动，实现人手模型的姿态变换。根据Kinect V2 相机内参数建立虚拟深度相机，通过投影过程将三维人手模型渲染成深度图像。

根据人手生理结构对各个关节运动的限制生成包含各个关节旋转角度的姿态信息文本。OSG 通过读取不同手势下的姿态信息文本控制人手三维模型各个自由度节点运动，实现人手三维模型的动作变化。将虚拟深度相机放置在人手模型正上方1 m 处，拍摄不同姿态下人手模型对应的深度图像。

人手模型的姿态变化包括三维人手全局姿态变化与局部手指关节姿态变化。为了获取合理的全局姿态，本文根据真实人手自然运动对人手模型的全局姿态变换范围进行约束。图5 为定义的三维人手模型旋转轴，其旋转范围约束如下：

图5 人手三维旋转轴示意图Fig.5 Schematic diagram of hand 3D rotation axis

局部手指关节变化通过5 个人手基本动作模板生成，动作模板T1，T2，T3，T4，T5 如图6 所示。动作模板中每一个手指关节可以在小范围内随机转动，以此生成基于模板的局部手指关节姿态。在生成姿态信息文本时，首先根据随机生成的局部手指关节姿态调整三维人手模型的手指变化，然后在限制范围内随机改变人手模型的全局姿态，最后记录变化后的姿态，输出信息文本。

图6 人手基本动作模板Fig.6 Basic hand motion template

本文采用上述方法生成共计2×104张分辨率175×175 的合成深度图像与对应的全局姿态标签。合成数据集部分实例如图7 所示。

图7 合成数据集部分实例Fig.7 Some examples of synthetic datasets

4.2 合成数据集实验

从真实深度相机直接获取人手全局姿态的真实值是非常困难的，故采用合成图像来对本文提出的方法进行量化评价。用于量化评价的测试集包含5 种基本人手动作，每种动作包含400张深度图像。网络模型在合成数据集上进行训练，使用随机梯度下降（Stochastic Gradient Descent，SGD）算法作为优化器，初始学习率设置为0.003 5，batch size 设置为96，epoch 设置为70。

4.2.1 超参数的选择

本文利用平衡系数α调整CNN 的损失函数。取平衡系数分别为4，6，8，10，12，14 来训练网络，图8 为本文采用不同平衡系数训练的模型在测试集上的预测结果。其中，包括人手全局姿态3 个欧拉角的绝对误差以及绝对误差均值。由此可以发现，当平衡系数α=10 时训练的模型在测试集上表现最好。在该参数下测量翻滚角、俯仰角、偏航角的绝对误差均值分别为3.689°，6.201°，5.218°，绝对误差平均值为5.036°。后续实验均在此参数设置下进行。

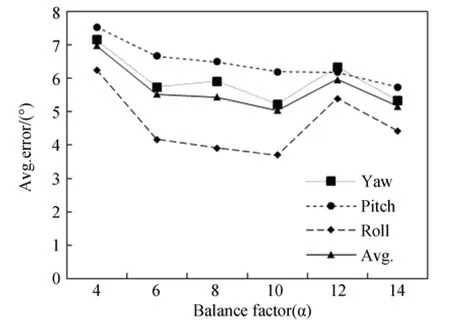
图8 不同平衡系数下人手全局姿态预测误差Fig.8 Prediction error of global hand pose under different balance factors

4.2.2 实验结果及分析

本文利用5 个基本动作模板生成5 个单一动作测试集。每个动作测试集中包含400 张同类动作不同姿态的人手深度图像与对应全局姿态标签。为每个动作测试集的400 次全局姿态预测结果计算绝对误差均值。表1 为本文方法对测试集中各类基本动作的预测结果。由此可以发现，本文方法测量动作T1，T2，T3，T4，T5 的人手全局姿态绝对误差均值分别为5.835°，5.669°，4.866°，4.275°，4.527°。其中，基本动作T1 的预测误差较大，其原因是该动作类似人手握拳动作，处于该动作的人手从不同的角度观测相似度非常高，具有歧义的手部外观会使模型预测结果产生较大的误差。

表1 各类基本动作的人手全局姿态预测误差Tab.1 Global hand pose prediction error for various basic actions （°）

为了证明本文所提出方法的有效性，与另外4 种方法进行了对比，5 种方法在测试集上预测结果的绝对误差均值如表2 所示。其中，Hopenet［18］是一种基于多损失深度CNN 的人体头部全局姿态估计方法，该网络使用ResNet50［22］作为主干特征提取网络，并使用平均绝对误差（Mean Aver-age Error，MAE）和交叉熵作为损失函数对网络进行训练优化。对比实验中，Hopenet［18］的回归系数设置为2。FSA-Net［19］是一种结合回归与特征聚合的人体头部全局姿态估计方法，该方法使用平均绝对误差作为损失函数进行训练优化。FSA-Net 使用文献［19］中方差评分函数进行特征聚合。方法1：采用基于像素投票的手部全局姿态估计网络结构，但手部全局姿态标签使用欧拉角表示。方法2：在方法1 的基础上移除解码器部分，不使用像素投票方法得出姿态结果，使用三层全连接层回归手部全局姿态欧拉角。表2为本文方法与对比模型在测试集上的结果，由此可以发现，本文方法的准确性明显优于其他方法。由此说明，本文方法更适用于手势多变的人手全局姿态估计任务，相比于FSA-Net 与Hopenet，本文方法能够为人手全局姿态的3 个参数提供更准确的预测结果，并且在翻滚角的预测精度上具有明显的优势。本文利用正弦值与余弦值表示手部全局姿态欧拉角的方法，相比于直接将欧拉角作为姿态标签的方法，精度更高。本文所使用的姿态表示方式更有利于神经网络对特征的学习。值得注意的是，方法2 相比于其他方法存在较大的误差，验证了基于像素投票的姿态估计方法的有效性。

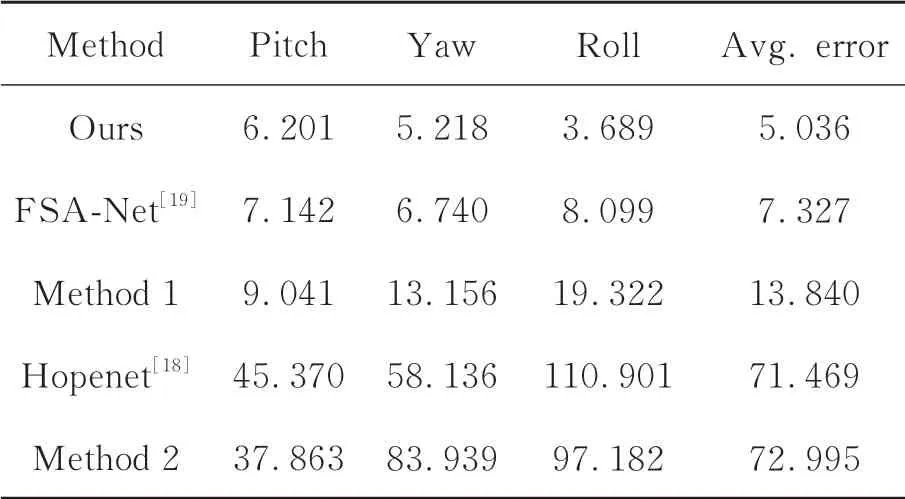
表2 不同方法在测试集上的人手全局姿态预测误差Tab.2 Global hand pose prediction error of different methods on test dataset （°）

参考其他全局姿态估计方法［17-18］，本文同样采用不同公差姿态预测精度来评估模型性能。不同公差姿态预测精度，即全局姿态预测绝对误差小于某个公差的准确率。图9 为不同方法在不同公差下对全局姿态各个参数的预测精度。可以发现，方法1 在公差值为5°时预测俯仰角的准确率最高，而在其他误差公差下，本文方法则具有更高的预测准确率。

图9 不同方法在测试集上的人手全局姿态预测精度Fig.9 Global hand pose prediction accuracy of different methods on test dataset

本文方法在NVIDIA TITANXP GPU 上对人手深度图像进行全局姿态估计的平均速度为30.52 frame/s，可以满足实时性要求。本文方法对每一张深度测试图像进行处理总耗时约为32.77 ms，其中图像读取与预处理用时约8.36 ms，模型前向传播与像素投票用时约24.41 ms。

4.3 真实深度图像测试

本文采用真实手部深度图对方法进行定性测试，使用Kinect V2 深度相机采集手部图像作为输入。利用深度阈值分割人手区域，再将人手区域图像裁剪成分辨率为175×175 的输入图像。本文方法对真实人手深度图像的全局姿态预测结果如图10 所示。图中，第一行为Kinect V2 深度相机采集的真实深度图像，第二行为本文方法对真实深度图像进行预测获得的人手全局姿态估计可视化图。由图10 可以看出，本文方法在Kinect V2 较为粗糙的深度数据下仍可稳健地预测人手全局姿态。

图10 真实人手深度图像全局姿态预测结果Fig.10 Global hand pose prediction results of depth image of real hand

5 结 论

本文提出了一种基于像素投票的方法，在变化的手势下估计人手全局姿态，采用语义分割的方法确定人手像素位置，通过手部区域的像素姿态投票信息来生成稳健、准确的估计结果。针对人手全局姿态数据集采集困难的问题，设计开发了人手数据集合成程序，为深度神经网络提供高质量的训练数据。实验结果表明，本文方法的人手全局姿态预测误差均值为5.036°，可以准确地从深度图像预测人手全局姿态，在人机交互、机器人模仿学习等领域具有广泛的应用前景。但本方法对于俯仰角的预测误差较大，在未来的工作中，将对模型像素投票处理方法进行优化，降低误差较大的投票对最终结果的影响，进一步提高预测精度。