比例时滞神经网络的全局多项式镇定性*
2022-10-28张诗茹张渝佶周立群
王 宇,张诗茹,张渝佶,周立群
(天津师范大学数学科学学院,天津 300387)
近年来,神经网络被广泛应用于联想记忆、信号处理、人工智能、优化与控制等领域,这些应用大都要求神经网络是稳定的.但由于在网络运行中时滞的存在不可避免,因此学者一直致力于研究时滞神经网络的各种稳定性[1-3].神经网络在控制器的作用下达到稳定时,称该网络是可镇定的.镇定性也是一种稳定性,学者对时滞神经网络镇定性也进行了深入研究[4-8].
比例时滞是一种客观存在的无界时变时滞,其优点是系统可根据网络所允许的最大时滞去控制网络的运行时间.2011年,周立群[9]将比例时滞引入神经网络,构建了比例时滞神经网络(Proportional Delayed Neural Networks,PDNNs)模型.单调递增的比例时滞函数使得系统时滞具有可控性和可预测性,故许多学者对PDNNs的动力学,尤其是稳定性[10-18](包括镇定性[19-22])进行了众多研究.例如,张保生[1]利用Lyapunov泛函方法、Barbalat引理和平均值不等式讨论了时滞细胞神经网络的稳定性;Zhou等[21]采用离散控制器,基于Lyapunov函数和LMI方法,获得了PDNNs的全局多项式镇定性和全局渐近镇定性判据.受文献[1,21]的启发,笔者拟针对一类PDNNs,采用状态反馈控制器,在激活函数有界且满足Lipschitz条件下,通过构造适当的Lyapunov泛函,并利用平均值不等式及其分析技巧,研究了该神经网络的全局多项式镇定性和全局渐近镇定性.
1 模型描述与预备知识
考虑如下PDNNs:
(1)

(H1) 在R上有界;
(H2) 满足Lipschitz条件,即存在常数li>0,使得
|fi(ξ)-fi(η)|≤li|ξ-η|ξ,η∈R,i=1,2,…,n.
为了使系统(1)镇定,取控制器ui(t)=-kixi(t),则系统(1)变为如下闭环系统:
(2)


其中α∈Z+.

注1全局多项式镇定性也是一种全局渐近镇定性,但其收敛速度比一般的全局渐近镇定性的收敛速度快.
引理1[1]若fi(·)(i=1,2,…,n)满足(H1)和(H2),则系统(2)一定存在平衡点.
引理2[1]若fi(·)(i=1,2,…,n)满足(H1)和(H2),则系统(2)的所有解在[0,+∞)上均有界.
引理3[1]若ai(i=1,2,…,n)为正数,则
(3)
2 全局多项式镇定性
令zi(t)=xi(et),则系统(1)和(2)分别变为
和
(4)

注3由定义1易知系统(2)与(4)具有相同的平衡点,即x*=z*.
定理1假设(H1)和(H2)成立,在状态反馈控制器ui(t)=-kixi(t)下,若存在α∈Z+和λ>0,使得
(5)

(6)

构造正定的Lyapunov泛函
其中α∈Z+,λ>0.沿系统(5)计算V(t)的上右Dini导数,由(H2),可得
(7)
根据平均值不等式(3),可得
(8)
(9)
将(8)和(9)式代入(7)式,可得
(10)
(10)式蕴含着V(t)≤V(lnt0),且
(11)

进而有
(12)


(13)

(14)
在(14)式中取σ=t,得到
于是由定义(2)可知系统(1)全局多项式镇定到它的平衡点x*.证毕.
定理2假设(H1)和(H2)成立,在控制器ui(t)=-kixi(t)作用下,若存在α-1∈Z+和λ>0,使得对于i,j=1,2,…,n,有


计算U(t)的右上Dini导数,可得
(15)
根据平均值不等式(3),可得
(16)
(17)
将(16)和(17)式代入(15)式,可得
(18)
于是U(t)≤U(lnt0),且
(19)

进而有
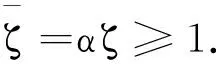
注4文献[1]中的系统为常时滞的,本研究中的系统为无界时滞的,时滞函数(1-qi)t依赖比例时滞因子qi的大小,因此就时滞函数而言,本研究推广了文献[1]的结果.另外,文献[1]中通过构造Lyapunov泛函、Barbalat引理和平均值不等式,得到的是常时滞神经网络的全局渐近稳定性,本研究中没有使用Barbalat引理,而是通过构造Lyapunov泛函和平均值不等式得到全局多项式镇定性,因此本研究所得结论更优.
3 全局渐近镇定性
定理1与定理2是对系统(1)进行非线性变换zi(t)=xi(et),在状态反馈控制器ui(t)=-kixi(t)作用下,得到系统(1)全局多项式镇定到它的平衡点x*.如果不进行该非线性变换,就只能得出系统(1)全局渐近镇定到它的平衡点x*.
定理3假设(H1)和(H2)成立,在控制器ui(t)=-kixi(t)作用下,若存在α∈Z+,使得
(20)

(21)
显然,平凡解y*=(0,0,…,0)T是系统(21)的平衡点.要证x*是系统(1)的全局渐近镇定的平衡点,只需证y*是系统(21)的全局渐近镇定的平衡点即可.
构造Lyapunov泛函
其中α∈Z+.沿系统(21)的解计算V(t)的上右Dini导数,根据平均值不等式(3)和(H2),可得
(22)
根据平均值不等式(3)和(22)式,可得
当y(t)=(y1(t),y2(t),…,yn(t))T≠0时,至少存在1个i,使得yi(t)≠0,于是由(20)式可得
因此D+V(t)<0.
当y(t)=(y1(t),y2(t),…,yn(t))T=0,y(qt)=(y1(q1t),y2(q2t),…,yn(qnt))T≠0时,有yi(t)=0(i=1,2,…,n),于是由(22)式的第1个等号关系,可得
当y(t)=y(qt)=0时,由(22)式的第1个等号关系,可得D+V(t)=0.
综上,当且仅当y(t)=y(qt)=0时,D+V(t)=0,其他情况都有D+V(t)<0.同时,当‖y(t)‖→+∞时,V(t)→+∞,即V(t)是径向无界的,因此系统(1)全局渐近镇定到它的平衡点x*.
定理4假设(H1)和(H2)成立,在控制器ui(t)=-kixi(t)作用下,若存在α-1∈Z+,使得对于i=1,2,…,n,有

证明构造Lyapunov泛函
其余证明过程类似定理2和定理3.证毕.
注5定理1~4的条件都依赖于比例时滞因子qi(i=1,2,…,n),因此本研究所得结果均是时滞相关的,能很好地反映出比例时滞因子对系统镇定性的影响.
注6在系统(1)中,当qj=1(j=1,2,…,n)时,本研究所得到结果仍然适用.
4 数值算例
例1考虑如下二维比例时滞神经网络:
(23)

图1 无控制器时系统(23)的时间响应曲线Fig. 1 Time Response Curves of System(23)Without Control

情况1当控制器ui(t)=0(i=1,2)时,系统(23)的从不同初值初始的时间响应曲线如图1所示.由图1可以看出,此时系统(23)是不稳定的.
情况2控制器ui(t)=-kixi(t)(k1=1.5,k2=2),e1=2,e2=2.5,取α=2,当i=1,2时,通过计算可得
这满足定理3的条件,因此由定理3可以判断系统(23)全局渐近镇定到它的平衡点(0,0)T.
情况3在情况2的条件下,取λ=1,α=2,当i=1,2时,通过计算可得
由定理1可知,系统(23)的平衡点(0,0)T是全局多项式镇定的.
系统(23)的相图和时间响应曲线分别如图2,3所示.由图2,3可以看出,此时系统(23)是稳定的.

图2 系统(23)的相图Fig. 2 Phase Trajectory of System(23)

图3 系统(23)的时间响应曲线Fig. 3 Time Response Curves of System(23)
例2考虑如下二维比例时滞神经网络:
(24)

情况1当控制器ui(t)=0(i=1,2)时,系统(24)的从(0,1)T初始的相图和时间相应曲线分别如图4,5所示.由图4,5可以看出,此时系统(24)是不稳定的.
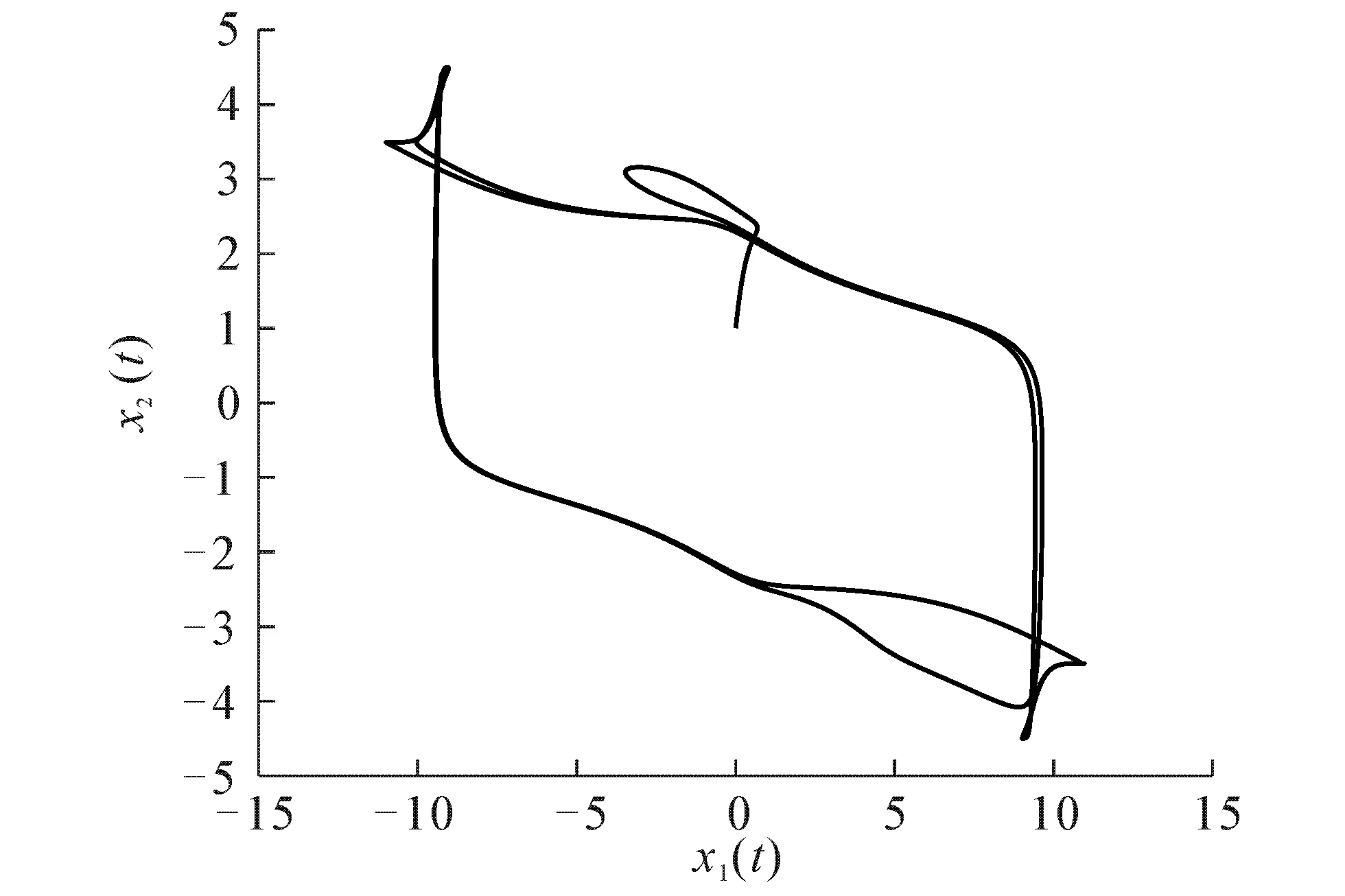
图4 无控制器时系统(24)的相图Fig. 4 Phase Trajectory of System(24)Without Control

图5 无控制器时系统(24)的时间响应曲线Fig. 5 Time Response Curves of System(24)Without Control

由定理4可知,系统(24)的平衡点(0,0)T是全局渐近镇定的.
情况3在情况2的条件下,取λ=1,α=2,当i=1,2时,通过计算可得
由定理2可知,系统(24)的平衡点(0,0)T是全局多项式镇定的.
系统(24)的相图和时间响应曲线分别如图6,7所示.由图6,7可以看出,此时系统(24)是稳定的.

图6 系统(24)的相图Fig. 6 Phase Trajectory of System(24)
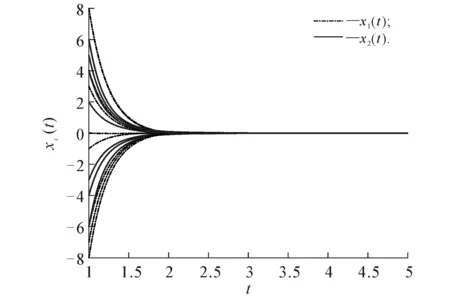
图7 系统(24)的时间响应曲线Fig. 7 Time Response Curves of System(24)
综上,对于系统(23)和(24),在控制器ui(t)(i=1,2,…,n)作用下,分别应用定理3和定理4,可得它们平衡点的全局渐近镇定性,分别应用定理1和2,可得它们平衡点的全局多项式镇定性.根据注1,全局多项式镇定性收敛速度快于渐近镇定性,这说明定理1和定理2优于定理3和定理4.
5 结语
研究了一类比例时滞神经网络的全局多项式镇定性,在状态反馈控制器作用下,通过构造适当的Lyapunov泛函,运用平均值不等式及其分析技巧,获得了保证系统时滞依赖的全局多项式镇定和渐近镇定的充分条件,并通过数值算例检验所得准则的有效性.本研究结果获得了相较全局多项式稳定性、全局渐近稳定性更优的结果,不足之处在于无法控制系统收敛到平衡点的速度.下一步笔者考虑如何让系统收敛的速度可控且尽量加快.
