串联超级电容器组的均压方法研究

宋倩，蓝俊欢

（河池学院大数据与计算机学院，广西河池 546300）

作为新兴的电容产品，超级电容有着远超普通电容的功率密度。离子或电荷的沉积和释放在电极表面通过电化学电荷转移过程导致其具有很大的能量[1]。对比传统电池，超级电容作为储能领域的新元件，其在一些性能指标，如循环次数、功率密度上优于前者，且对环境污染小[2-3]。作为新兴储能元件的代表，超级电容无疑吸引了开发和技术人员的目光，在新能源领域有较好的应用前景[4-5]。

超级电容器单体的电压相对较低，在电压需求较高场合，最简单的方法是连接多个超级电容单元，此时全体超级电容的电压之和就是串联超容组的总电压[6]。由于工艺原因，超级电容器电容和内部电阻的差异是不可避免的。使用时，为了延长串联超容组寿命，并提高超级电容的能量利用率，串联超容组的电压均衡措施或电路是必不可少的[7-8]。

目前串联超容组的均压方法主要从两个方向划分[9-10]。能耗式均衡是常见的均衡方法，有并联电阻法、开关电阻法、并联二极管法等[11]。其通过直接消耗电压偏高单体的能量来实现，过程中能量转变为热量消散了，最终达到所有单体电压的一致。能耗式电压均衡优势明显，所需器件数目少、控制简单、可靠性高。但系统的能量只能消耗掉而不能加以利用，均衡的快慢很大程度上取决于电路的散热条件，均压效率较低、速度慢[12-13]。与能耗式均衡对应的是非能耗均衡，非能耗电压均衡方法包括DC/DC 变换器法、多绕组变压器法、飞渡电容法等[14]。均压措施是低压超级电容获得由高压超级电容通过均压方法转移来的能量，最终全部的超级电容电压相等，实质是内部能量的转移和分配。非能耗式均衡方法发热量小，无附加损耗，在均衡电流、速度、效率等方面都较能耗式有显著优势，在高电压大容量场合得到了广泛应用，但电路较复杂、开关和磁性元件较多、成本较高[15]。

文中在分析已有能耗型和非能耗型串联超容组电压均衡电路的基础上，从减少所用开关器件数量、降低电路控制难度、易于扩展应用到多个串联超级电容等角度考虑，设计一种DC/DC 变换器法串联超容组电压均衡电路。先后对电路工作原理进行分析，搭建仿真电路进行验证，结果表明其实现了电压均衡的功能。

1 超级电容器的等效模型

超级电容器的结构本质上是一个复杂的电容网络，每个电容器单体都有自己的内部电阻、电容和相应的时间常数。

最简单的等效电路模型是串联RC 电路模型，如图1 所示。该模型结构简单，适合理论分析。等效模型是理想电容器C和等效串联电阻ESR 的串联连接。ESR 表征了超级电容器内部的热损耗。随着放电电流的变化，ESR 会经历不同的电压降，ESR 对单体的最大放电电流具有限制作用[16]。文中使用串联RC 模型进行分析。

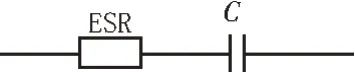
图1 超级电容串联RC模型

2 均压电路及其基本原理

Sepic 变换器是一种常见的直流-直流变换器，被广泛应用在多种电压转换场合，其通过调节电路的占空比，可以实现升高电压和降低电压的功能，而且其具有输入电流连续的特点。下文依次阐述Sepic 变换器、组合式Sepic 变换器的基本工作原理，最后分析基于组合式Sepic 变换器的串联超级电容器组的电压均衡电路工作原理。

2.1 Sepic变换器

Sepic 变换器可工作于电流连续或电流断续模式，下文对其基本工作原理进行阐述，基本Sepic 变换器拓扑如图2 所示，依次介绍其工作模态一和二。

图2 基本Sepic变换器拓扑

模态一[t0,t1]（见图3）在t0时刻，开关管S导通，二极管D 截止，形成Vin-L1-S回路，电感L1上的电流线性增长。形成C1-L2-S回路，电感L2上的电流也线性增长，电容Co为负载电阻R提供能量。电压方程式如式（1）:

图3 Sepic变换器工作模态一

模态二[t1,t2]（见图4）；在t1时刻，开关管S截止，二极管D 导通。形成Vin-L1-C1-D(R)回路，电感L1上的电流线性下降。形成L2-D-Co(R)回路，电感L2上的电流线性下降。电压方程式如式（2）:

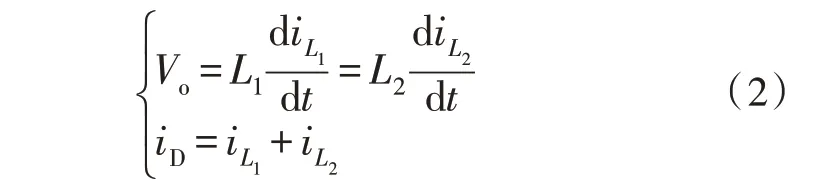
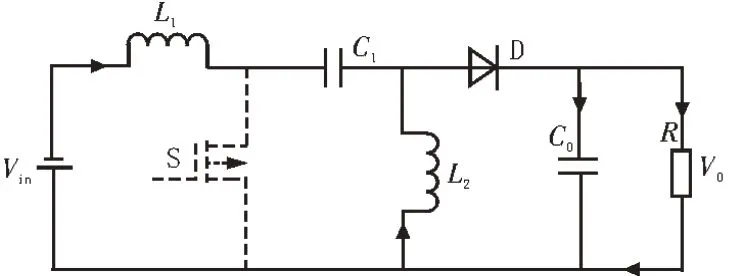
图4 Sepic变换器工作模态二

联立式（1）和（2），可以求出电感L1上的电流和电感L2上的电流的增量和减量的表达式，如式（3）所示：

式（3）中，D代表占空比，T代表开关管周期。根据伏秒平衡原理，可以求出Sepic 变换器的电压变换比。如式（4）所示：

2.2 组合式Sepic变换器工作原理

为减小变换器体积，减少损耗，提高变换器升压比，文中采用一种组合式Sepic 变换器，如图5 所示。

图5 组合式Sepic变换器拓扑

组合式Sepic 变换器工作原理阐述如下：

工作模态一[t0,t1]（见图6）t0时刻，开关管S 导通，二极管D1和D2截止。形成Vin-L1-S 回路，L1上的电流线性上升。形成C3-S-L3回路，电容C3为电感L3提供能量，L3上的电流线性上升。形成C1-S-C4-L2回路，C4为电容C1和电感L2提供能量，L2上的电流线性上升。形成C4-C2-R回路，C2、C4向负载释放能量。

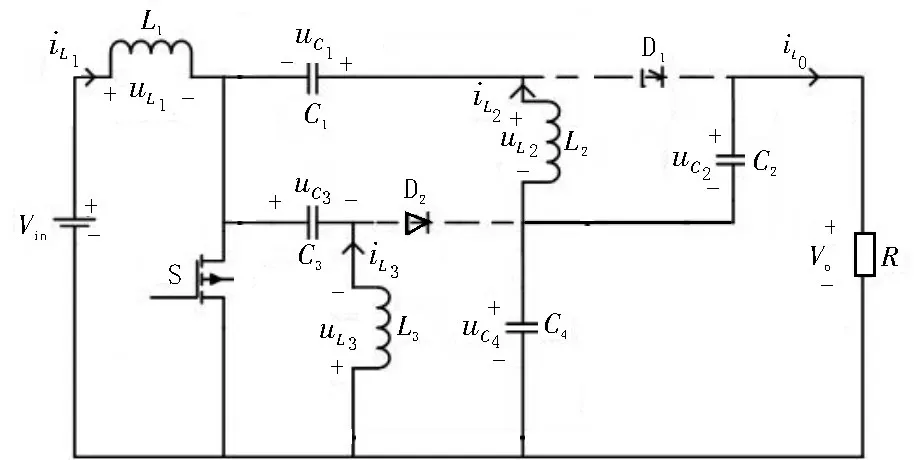
图6 组合式Sepic变换器工作模态一

有以下等式成立：

式（5）中，L代表电感器的自感，M代表电感器的互感。

工作模态二[t1,t2]（见图7）此模态过程相较模态一和三时间非常短，t1时，开关管S断开，二极管D1导通。通过二极管D1、电源Vin、电感L1和电容C1向负载电阻R提供能量，同时向电容C2和C4提供能量，此时，电感L1的电流将线性减小。形成L2-D1-C2回路，并且L2上电流也线性减小。由于开关管S 断开，电感L2两端的电压反向，此时有，因此，二极管D2截止，电感L3经由电容C1和C2释放能量，电感L3的电流线性减小。

图7 组合式Sepic变换器工作模态二

各回路的电压方程可表示为：

工作模态三[t2,t3]（见图8）t2时，开关管S断开，二极管D1导通，形成Vin-L1-D1-C2-C4和Vin-L1-C1-D1-R回路，电感L1上的电流继续呈线性下降。电感L3两端的电压继续反向升高，当电压高于电容C4端电压时，二极管D2导通，形成L3-D2-C4回路，L3上的电流线性下降。此时，形成Vin-L1-C3-D2-C4回路，L1上的电流线性下降。

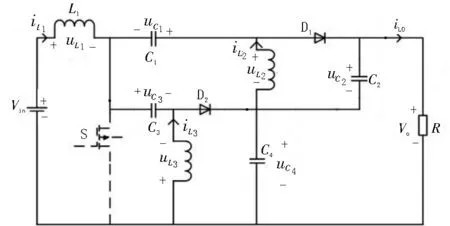
图8 组合式Sepic变换器工作模态三

各回路的电压方程为：

式（8）在三个模态下均成立。

模态二的持续时间非常短暂，因此忽略其对变换器电压增益的影响，由式（5）-（8）计算可知，电感L1、L2、L3上的电流增量和减量分别为：

联立式（8）-（11），并依据伏秒平衡原理，求出组合式Sepic 变换器的电压变换比为：

由变换比公式可知，组合式Sepic 变换器的升压比是基本Sepic 电路的两倍，更适合运用在较高电压需求的场合。

2.3 组合式Sepic电路的串联超级电容器组均压电路

该文采用了一种基于组合式Sepic 电路的电压均衡电路，如图9 所示。该电路只需要一个开关管，传统均衡器不仅需要大量开关，而且还需要传感器或变压器（与串联连接的数量成比例），与传统均衡器相比，其单开关配置可以显著降低电路复杂度。除了开关的数目外，该均压电路还可以简化其驱动电路。在DCM（电流断续）的情况下，可以消除反馈控制，换而言之，超级电容电压不平衡可以通过固定的占空比操作来平衡，并且不需要进行电压测量。因此，实现电压均衡不需要电压检测电路，与传统均衡器相比，所提出的电压均衡电路得到进一步简化。

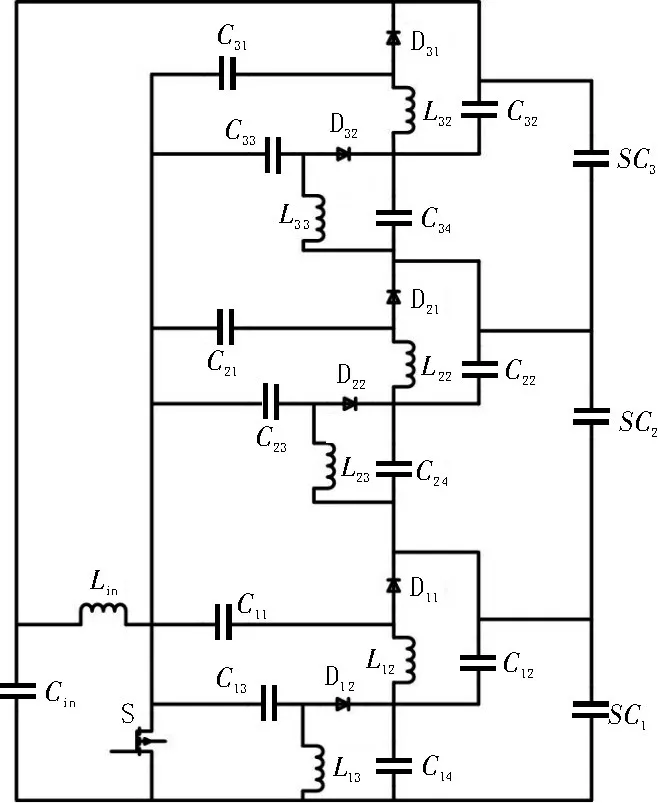
图9 组合式Sepic电路的串联超级电容器组均压电路

下面分析组合式Sepic 电路的均压原理。V1、V2、V3分别为超级电容SC1、SC2、SC3的电压，假设单体SC2电压V2最低。

超级电容SC1-SC3为组合式Sepic 电路提供能量，在开关管S 导通阶段，Lin、L22、L23、L32、L33的电感电流增大，电感储存一定的能量，电流通过电感L22、L23、L32、L33和电容C22、C23、C32、C33流向开关管S。在开关管S 关断阶段，电感中存储的能量最先分配给电压最低的超级电容SC2，二极管D21导通。由于二极管D11-D32的平均电流等于电感L12-L33的平均电流，所以电感Li的平均电流为零，只有纹波电流流过。当二极管D21上的电流降到零时，电路中的电流保持恒定。随着能量的分配，串联超级电容器的单体电压逐渐达到均衡状态，此时电感L12-L33、电容C11-C32以及二极管D11-D32的电流波形分别一致。

由推导可知电感L上的电流满足下式：

3 仿真分析

使用PSIM 电路仿真软件来仿真和分析串联超级电容器组的组合式Sepic 均衡电路，如图10 所示。开关频率为20 kHz，u1(0)=1 V，u2(0)=2 V，u3(0)=2.7 V分别为SC1、SC2、SC3的初始电压。

图10 组合式Sepic变换器均压仿真图

均压电路各元件参数如表1 所示。

表1 均压电路元件参数表

使用基于组合式Sepic 电路的串联超级电容器组电压均衡电路来测试系统的均衡效果。由仿真结果知SC1的电压逐渐上升，SC2的电压缓慢下降，SC3的电压下降速度稍快。大约1.3 s后，超级电容器组的单体电压达到平衡。电压均衡过程的示意图如图11所示，单体电压差最终减小到0.1 V 以内。

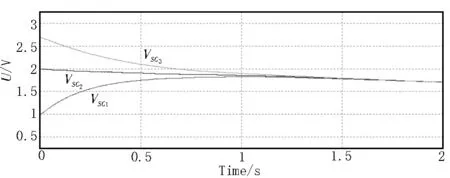
图11 三单体均压波形图

由仿真结果可知，该电路可以均衡串联超级电容器组各单体电压，均压速度较快，能有效提升储能系统的性能。

4 结论

采用基于组合式Sepic 电路的电压均衡电路。该电路仅具有一个开关管，简化了电路结构，且占空比和开关频率是固定的，无需反馈控制，控制难度低。分析了DCM 模式下电路的电压均衡原理，最后，对由三个超级电容组成的串联超容组进行仿真测试。从仿真结果图可以看出，该电压均衡策略的电压均衡时间较短，具有一定参考价值。