液态工质储罐冷端参数对压缩气体储能项目全流程侧的重要性
2022-10-27范立华王松翟璇罗方靳亚峰
范立华,王松,翟璇,罗方,靳亚峰
(东方电气集团东方汽轮机有限公司,四川 德阳,618000)
0 引言
压缩气体储能是一种安全可靠性高、机组容量大、电电转换效率高、地域适应性好、寿命期长、响应时间达分钟级、建设成本及全周期度电成本较低的主流储能型式,未来极具发展优势。
对于压缩气体储能,虽然具有地域适应性好的特点,但是其储释能系统需配备一定的储存装置,用以在储能侧和释能侧高压低温工质的存放。一般其储存装置可分为2 种:(1)位于地下的大容积盐穴或煤矿巷道;(2)放置于地面的储罐装置。对于地面的储罐装置,常常需要考虑其设备投资占比的属性,过大的储罐装置对于系统的整体投资占比极大,这也成为了压缩气体储能系统中重要的掣肘因素,而以液态形式存放工质的液态压缩气体储能项目则由于具有较大的存储密度,往往在储罐设备上具有较大的优势。
对于此液态气体储能发电系统,通过合理配置冷端储罐的参数,可以在已有储罐装置前提下,不增加系统其他设备投资的情况下有效提高储释能系统的运行时长。同时对于储能初始状态下一定质量的气体工质,通过优化其冷端储罐的参数,可以有效延长运行时长。
1 理论基础
1.1 液态压缩气体储能系统
压缩气体储能系统通常由储能模块和释能模块构成。
储能模块由低参数工质气仓(或直接取自大气)、压缩机、换热器1、储热罐、储气/液罐构成。储能时间段内,压缩机消耗电能将气仓中低参数的气体工质压缩为高压高温的气体工质,然后经换热器1 将高参数的工质转换为高压、低温的气体或液体工质,其热能储存于储热罐中,换热后的高压、低温气体或液体工质储存于储气/液罐中。
释能模块由储热罐、储气/液罐、换热器2、透平、低能工质气仓(或直接排气至大气)构成。释能时间段内,换热器2 开始工作,储气/液罐出来的高压低温工质吸收储热罐中高温储热介质的热能,升温为高压高温的工质气体,然后经过透平膨胀做功,完成储能系统做功侧的功率要求,最后膨胀做功完成后的低参数工质气体可根据工质性质排至大气或排至某密闭的低温低压气仓。
在储能模块与释能模块,可以看到2 种不同的工作时段均有储热罐、储气/液罐工作的部分。在整个储释全过程时段内均要满足储热罐、储气/液罐中储热介质和工作工质的流量和热量平衡。
本文主要研究对象为储液罐装置,通过对液态储罐中不同容积、温度、工质质量的情况进行分析,得到系统侧相关参数的变化趋势和储能时长等重要参数的变化规律,以此进一步优化设计系统。图1 为某液态气体储释能系统的储气/液罐装置及相连接系统。图2 为某储气/液罐结构示意。

图1 某压缩液态气体储释能系统
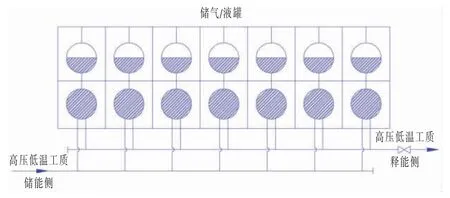
图2 某储气/液罐结构示意图
1.2 储罐中气液两相形式物性假设
在压缩气体储能系统冷端储罐中,储释能系统侧工质实际以气相和液相共存的形态同时存在,极限形态下,储能侧工质来自压缩机出口,以气相形式存在,并经过换热器1 进行放热,当储能过程结束时,该部分气体形态应完全转变为液态。
由于压缩机出口至储罐的压力范围波动极小,简化处理认为其压力相同,将该过程简化假设,即储能侧工质应在某压力下由气相完全转变为液相,同理,当系统进入释能时段时,认为释能侧工质在某压力下由液相完全转换为气相。
考虑到储罐中应始终维持压力值,因而实际中工质不可能完全转换为液相,该假设与实际过程中具有一定偏差,但对于系统的定性分析及对比论证结构,具有理论分析意义及实际工质参数参考价值,在实际中可适当增加工质气量以维持储罐中的压力值。另外,假设储罐在储能和释能中始终处于恒温过程态。
2 3 种不同边界条件下储罐及系统侧各重要参数的相互关系及变化趋势
对于液态压缩气体储能系统,液罐对应3 个重要性能参数:储罐容积、储罐工作的温度/压力、储罐中初始态的工质质量。上述3 个参数两两耦合且相互影响,并直接影响系统侧其他参数及循环性能。下面针对上述3 个参数形成的3 种组合形式进行详细分析,进而得到其具体变化趋势。
2.1 储罐温度/压力参数维持不变时,储罐、储释能气量、储释能时长及其他系统侧重要参数的关系
假设储罐温度/压力相同,仅在储能初始状态时设置不同的工质质量。经过计算,可得到储罐对应的容积大小、储能时长、储能侧终态质量、释能初态/终态质量、释能时长、热罐中换热介质的流量等参数的变化趋势。
(1)储罐容积的变化趋势
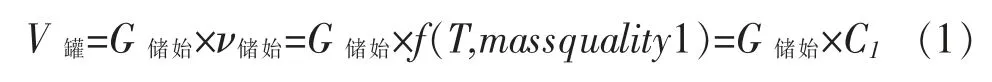
式中ν储始是某温度时储罐中工质全部为气态时的比容,该值在压力或温度给定的情况下为定值f(T,massquality1)=C1。
根据式(1)可得到V罐和G储始之间成正比关系,如图3 所示。
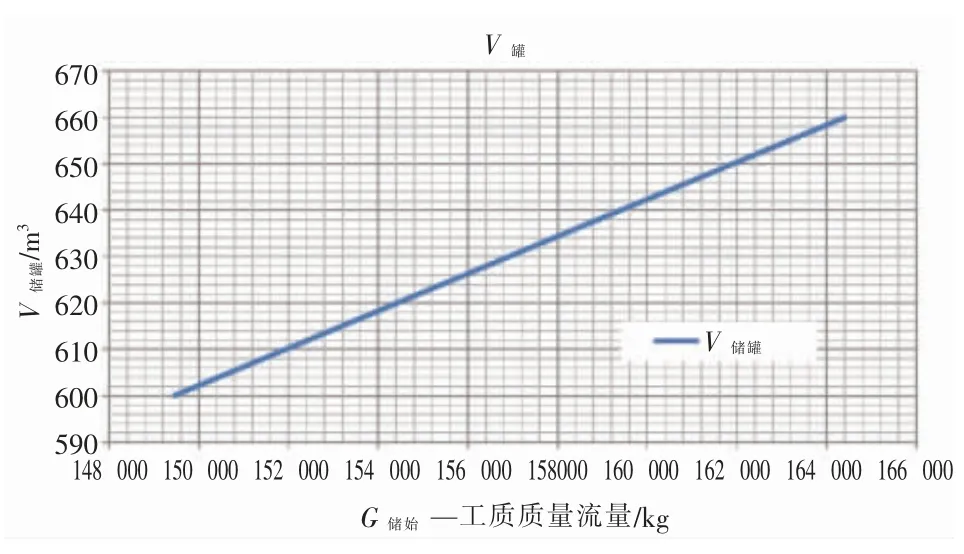
图3 储罐温度/压力相同,G储始与V罐的关系曲线
(2)储释能侧工质质量的变化趋势
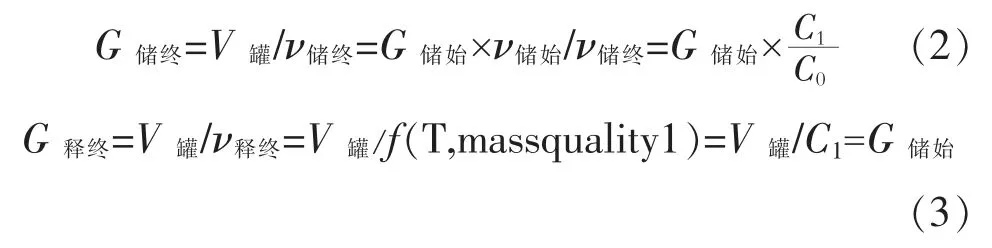
ν储终是某温度时储罐中工质全部为液态时的比容,该值在压力或温度给定的情况下为定值f(T,massquality0)=C0。
当储罐温度给定时,ν储始/ν储终=C1/C0为定值,因而式中G储终与G储始成正比变化趋势。储罐内工质质量在储能终态和释能初态是连续的,因而G释始=G储终。同时根据公式可得到G释终=G储始。图4 为储释能侧工质质量随G储始的变化趋势。
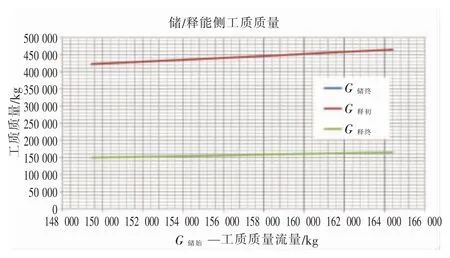
图4 储罐温度/压力相同时,储释能侧工质质量与G储始的关系曲线
(3)储能时长、释能时长的变化趋势
储能时长t储计算公式如下:
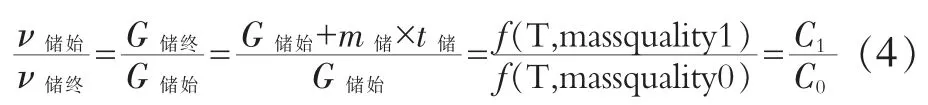
即:

同理,释能侧工作时长t释的计算公式如下:

即:
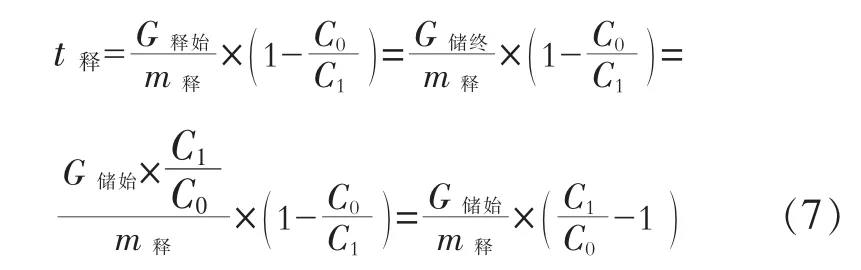
释能侧工质质量流率变化与透平侧工质流量变化率直接相关,对于液态储罐性质的储气介质,其释能侧透平进口压力稳定,因而可认为透平工质质量流率始终保持一致,即释能侧单位质量流率m释恒定。因而在此基础上释能工作时长t释也与储能侧初始质量G储始成正比变化趋势。
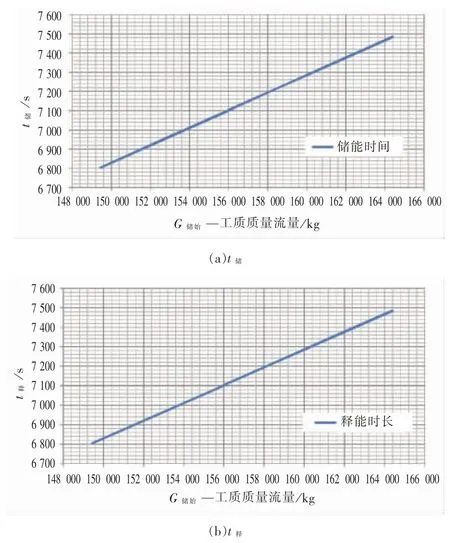
图5 储罐温度/压力相同时,t储、t释与G储始的关系曲线
对比t释和t储的公式可以发现,两者形式一致,均与G释始成正比关系,只是m储和m释的位置存在差异。如果储能侧储罐入口质量流率和释能侧储罐出口质量流率一致,则可能存在t释=t储的可能性。但是否真正可实现t释=t储,还需要增加其他判断条件,即储能侧和释能侧储热介质的热量和流量是否匹配。
(4)储释能侧储热介质质量、热量、压缩机耗功量、透平做功量、电电转换效率的变化趋势
当储罐温度/压力相同,仅在储能初始状态时设置不同的工质质量时,储能侧和释能侧系统关键参数如储热介质流量、热量、压缩机耗功量、透平做功量等均呈现一种与时间相关的积分积叠规律。
对于系统整体电电转换效率,数值上等于压缩机耗功量与透平做功量的比值,当两者均呈现相同的时间积叠关系时,系统整体电电转换效率将保持不变,如图6 所示。
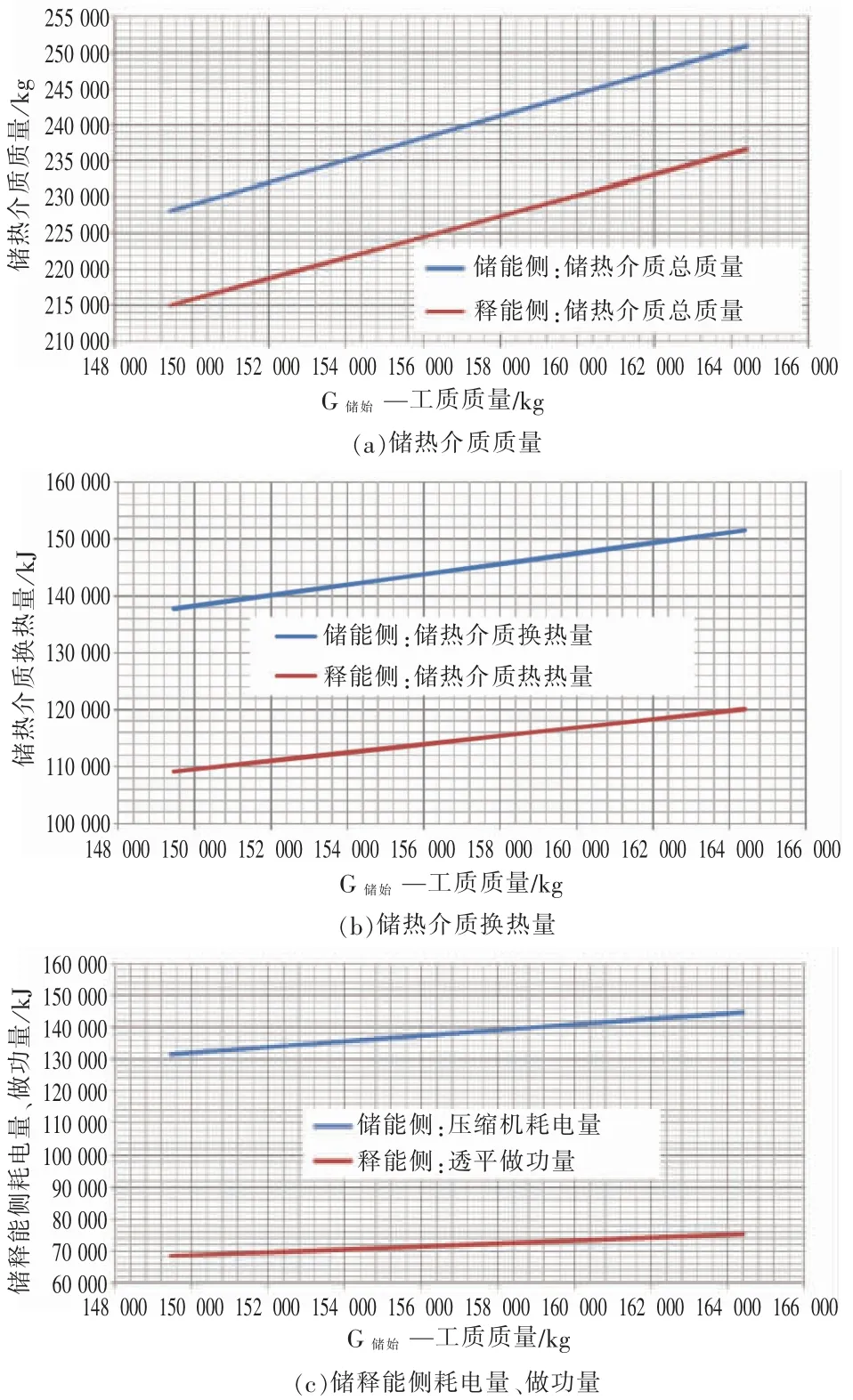
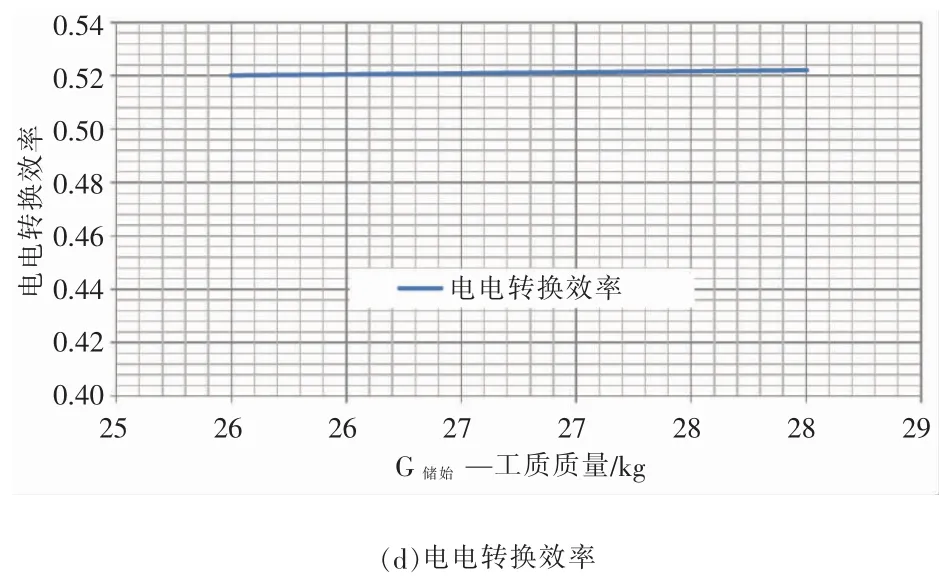
图6 储热介质质量、储热介质换热量、储释能侧耗电量、做功量、电电转换效率与G储始的关系曲线
2.2 储罐维持不变时,储罐冷端参数与储释能气量、储释能时长及其他重要系统侧参数的关系
假设储罐比容始终保持不变,但是对储罐冷端温度/压力设置不同的数值,可根据相关规律得到工质气量变化、储释能时长变化、系统侧其他重要参数变化趋势。
对于储罐处于某一温度/压力状态下时,储能侧与释能侧满足以下公式:
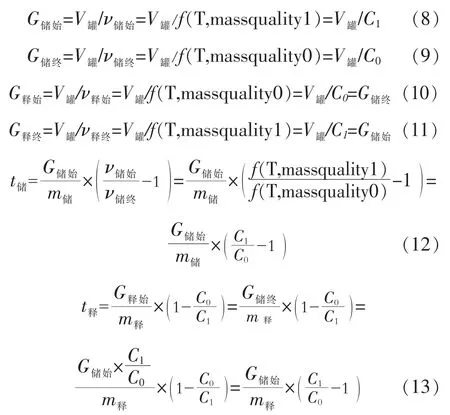
式中可看出,储罐在储能侧和释能侧不同时刻的质量只与当前工质该温度下对应的比容相关,且呈现反比关系。因此G储始=G释终,G储终=G释始,当然后者等式在任何情况下恒成立。同时储能的工作时长、释能的工作时长只与储罐在储能侧和释能侧质量流率相关。
(1)储释能初终态工质质量的变化趋势
当储罐容积固定而温度不同时,储释能初终态工质与该温度时工质比容/密度直接相关。图7、图8 为储释能初终态工质、储释能初终态密度与储罐温度的关系曲线。可以看到,储释能初终态质量与其对应状态的密度具有相同的变化趋势。

图7 储释能初终态质量与储罐温度的关系曲线
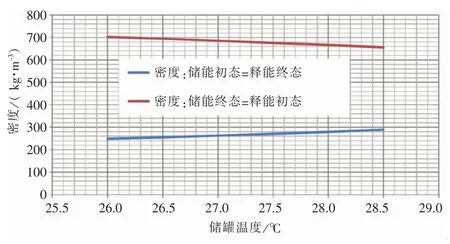
图8 储释能初终态密度与储罐温度的关系曲线
(2)储能侧与释能侧工质工作时长的变化趋势
当储罐处于不同温度/压力状态下时,储能侧与释能侧工质的工作时长与储罐温度成反向变化关系,上述关系可以通过公式推算得到,当储能侧和释能侧质量流率相同时,t储=t释∝。现列举储释能侧工作时长、(C1-C0)/(C1*C0)与储罐温度的关系曲线,如图9、图10 所示,对比两曲线图可以发现两者随储罐温度具有相同的变化趋势。
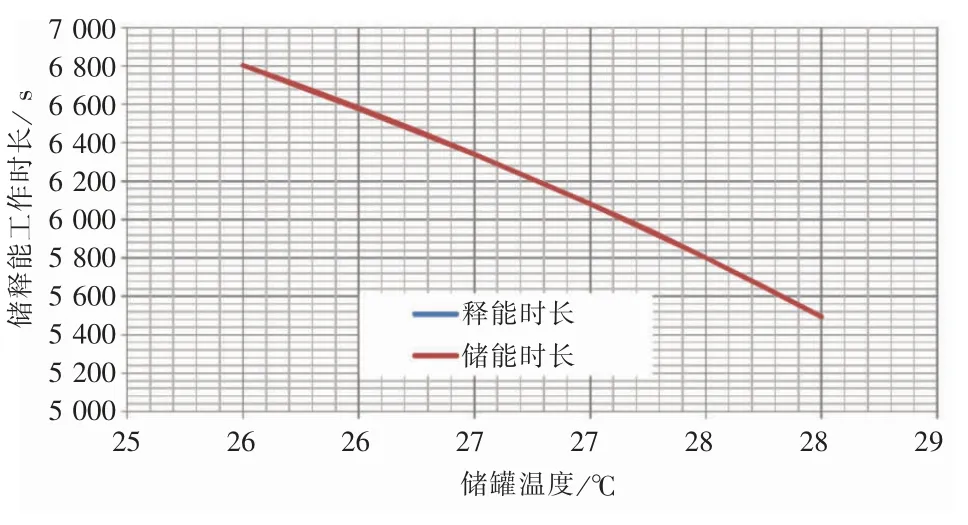
图9 储能侧与释能侧工质工作时长与储罐温度的关系曲线
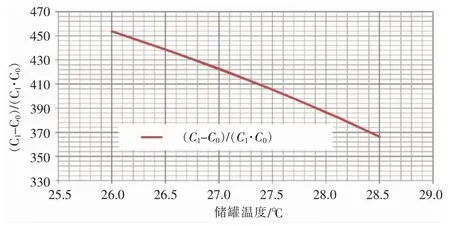
图10 (C1-C0)/(C1*C0)与储罐温度的关系曲线
(3)储释能侧储热介质质量、热量、压缩机耗功量、透平做功量、电电转换效率的变化趋势
当储罐容积相同而温度/压力不同,储释能侧单位质量流率m储=m释时,随储罐温度/压力的升高,压缩机和透平功率均将提高,但并不一定呈现线性的变化规律。与之直接相关的系统侧关键参数:单位时间内储热介质的质量、热量虽然会升高,但并不一定会呈现线性上升趋势。
在计算储能侧与释能侧关键参数规律时,需要计算的不仅仅是单位时间内的数据变化规律,还有储能侧与释能侧的运行时长,对系统侧关键参数的定性变化规律及趋势起到决定性作用。
根据储能侧与释能侧运行时长的差异,同时根据单位时间内压缩机、换热器1、换热器2、透平等众多设备引起的综合变化规律进行积分计算得到以下各关键参数的规律,如图11 所示。
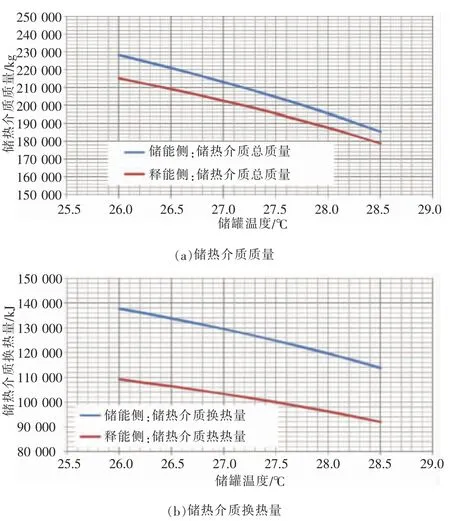

图11 储热介质质量、储热介质换热量、储释能侧耗电量、做功量、电电转换效率与储罐温度的关系曲线
从图11 中可以看到,储释能侧储热介质质量、储热介质换热量、储释能侧耗电量、做功量等几乎与工作时间成正比关系,仅有微小改变。与此同时,对于储罐在不同的温度/压力参数时,电电转换效率呈现微小量提升,几乎可以认为不变。
2.3 储释能初始气量不变时,储罐V、储罐冷端参数、储释能时长及其他重要系统侧参数的关系
对于特殊气体介质构建的压缩气体储能项目,其储释能气体的耗量也将对系统的整体成本产生较大影响。针对此种情况,假设储罐中储能初始状态下工质的质量始终保持不变,对储罐冷端温度/压力设置不同的数值,可根据相关规律得到储罐容积大小、储释能时长变化、系统侧其他重要参数变化如下。
(1)储罐所需容积的变化趋势
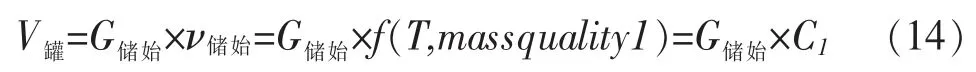
C1与储罐所处的温度/压力成反比,当储释能初始气量维持不变时,V罐大小只与C1正相关,因V罐而与储罐所处的温度/压力成反比关系。图12 为C1和V罐随储罐温度的关系图示。
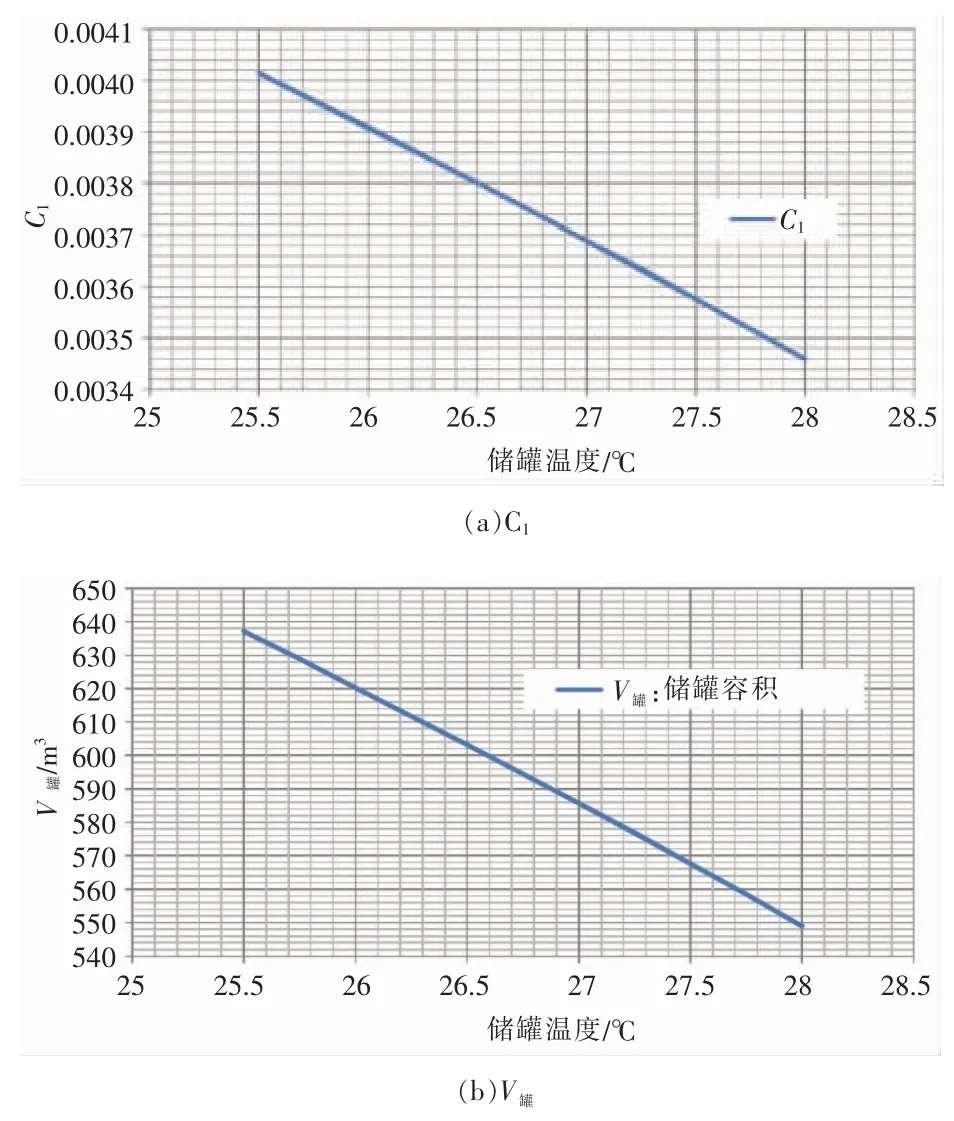
图12 C1 和V罐与储罐温度的关系曲线
(2)储释能初终态工质质量的变化趋势
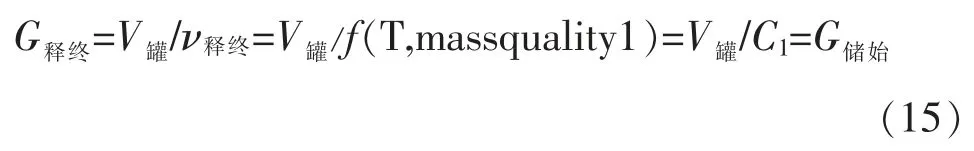
G释终的数值与V罐成正比,同时与C1成反比,考虑到V罐和C1均与储罐所处的温度/压力成反比关系,所以当储释能初始气量维持不变时,G释终=G储始始终保持不变。
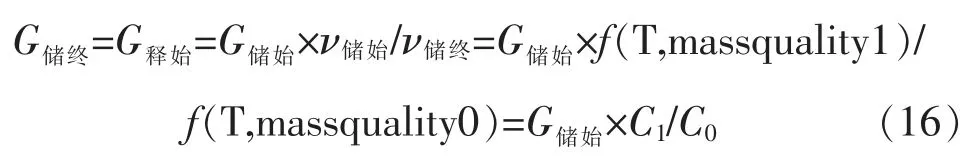
C1/C0与储罐所处的温度/压力成反比,所以当储释能初始气量不变时,G储终=G释始也与储罐所处的温度/压力成反比。图13 为C1/C0和G储终=G释始随储罐温度/压力状态参数的关系。
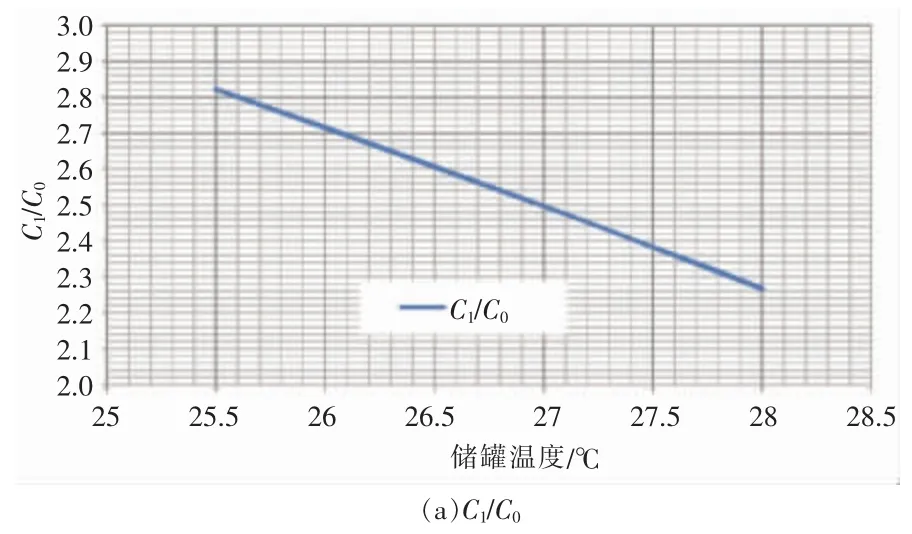
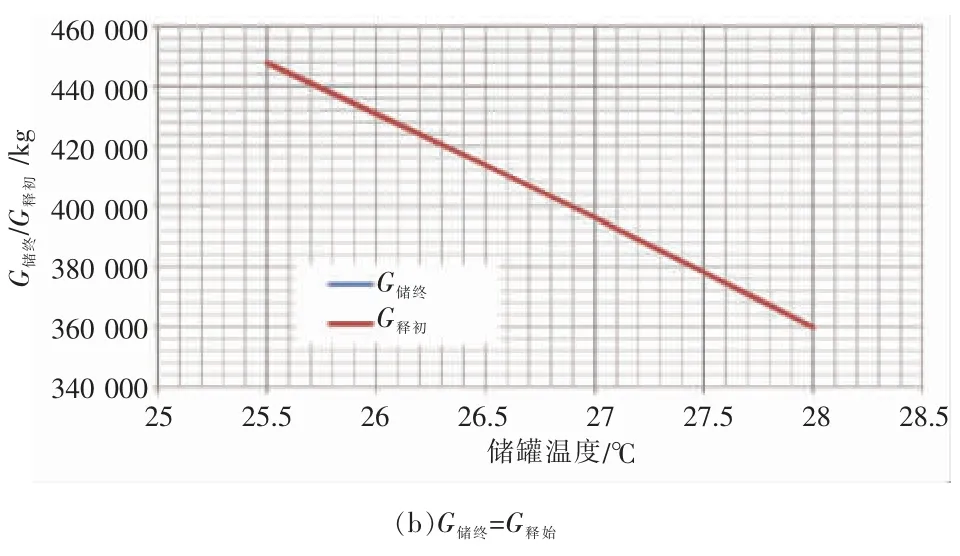
图13 C1/C0 和G储终=G释始与储罐温度的关系曲线
(3)储释能侧工作时长的变化趋势
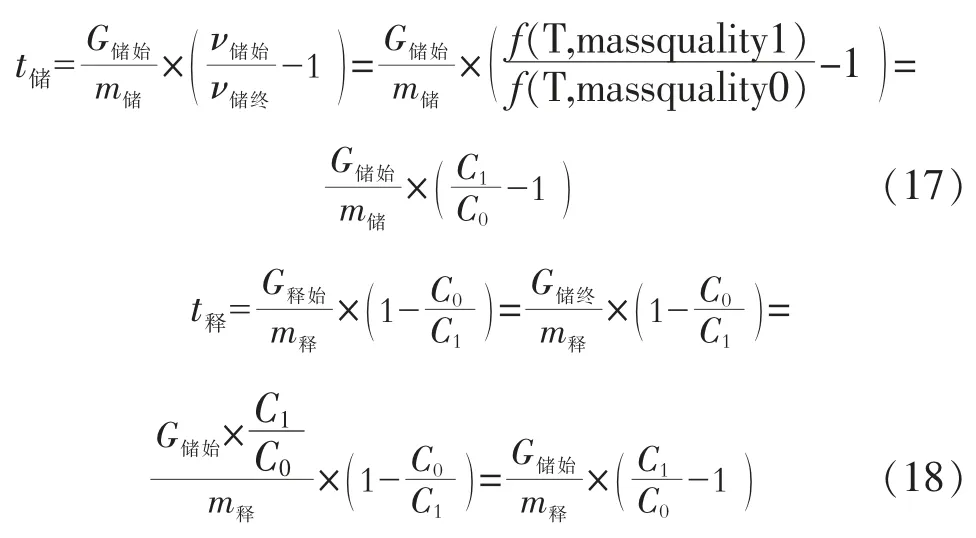
当储释能初始气量维持不变,且当储能侧压缩机和释能侧透平单位质量流率m储和m释相同时,t储=t释,且两者均与-1 成正比。图14 为-1 和t储=t释随储罐温度/压力状态参数的关系。

图14 C1/C0-1和t储/t释与储罐温度的关系曲线
(4)储释能侧储热介质质量、热量、压缩机耗功量、透平做功量、电电转换效率的变化趋势。
从图15 可以看到,储/释能侧储热介质质量、储热介质换热量、储能侧耗电量、释能侧做功量等几乎与工作时间成正比关系,仅有微小改变。与此同时,对于储罐在不同温度/压力参数时,电电转换效率呈现微小量提升,几乎可以认为不变。

图15 储热介质质量、储热介质换热量、储释能侧耗电量、做功量、电电转换效率与储罐温度的关系曲线
3 结论
对于冷端储罐以液态形式储存的压缩气体储能项目,其冷端储罐的参数对储-释能系统全流程侧均具有重要影响。考虑到压缩气体储能项目中冷端储罐的容积占系统比例极大,同时对非常规工质或有机工质而言其成本占比也极高。因此分析该系统的冷端储罐参数对整体系统经济性能具有较大意义,经过上文综合分析可得到以下结论:
(1)当储罐温度/压力保持不变时,V罐、G储终、G释始、G储终、t储、t释、储/释能侧储热介质质量、储热介质换热量、储能侧耗电量、释能侧做功量等参数均与G储始成正比关系。此时若想增加系统工作时长,需在等比例增加储罐容积的基础上,等比例增加储罐中工质的质量。
(2)当V 罐保持不变时,G储始、G 释终与储罐的温度/压力成正比变化关系,而其他参数如G储终、G释始、t储、t释、储/释能侧储热介质质量、储热介质换热量、储能侧耗电量、释能侧做功量等参数均与储罐的温度/压力成反比变化关系。此时,在保持液罐容积不变、且不增加系统其他设备投资的情况下,适当降低储罐温度,同时适当增加储罐中的工质质量,可以明显增加系统储能/释能的工作时长。或者当工作时长保持不变时,可以适当增加系统输出功率。
(3)当G储始保持不变时,G释终也将保持不变,而对于其他参数如V罐、G储终、G释始、t储、t释、储/释能侧储热介质质量、储热介质换热量、储能侧耗电量、释能侧做功量等参数均与储罐的温度/压力成反比变化关系。此时,若想增加系统的工作时长,需在等比例增加储罐容积的基础上,等比例降低储罐的温度。
在上述3 种不同的储罐冷端变量发生时,可以看到系统工作时长主要与储罐容积、储罐的温度、储罐中的工质质量这3 个参数有关,而这3个变量两两耦合。若想增加系统工作时长,在任意2个参数确定时,另一个参数将随之变化。通常情况下,储罐容积增加、储罐温度下降、储罐中工质质量增加可以增加系统的工作时长,可以在不增加系统侧其他设备投资的情况下,有效增加系统的工作时长或系统功率。
另外可以看到,对于其他系统侧参数,如储热介质换热量、储能侧耗电量、释能侧做功量等均与工作时间成正比关系,而电电转换效率整体变化不大。
