基于启发式算法的乏燃料装料排期计划研究
2022-10-27黎知行李仕元景顺平
苏 康,黎知行,史 骥,李仕元,景顺平
[1.中广核(北京)仿真技术有限公司,深圳 518031;2.中广核铀业发展有限公司公司,北京 100029]
我国商用核电站乏燃料的去向一般为离堆干式贮存或后处理。传统乏燃料运输方式是单起点与单终点“门到门”的公路运输,单批次运输2~3个货包。随着核电站增多,原有的运输模式已不能适应当前乏燃料离堆的紧迫性需求。近年来我国开展了乏燃料多式联运建设,单批次最大运输量提升到10个货包,传统公路运输单批次运输模式对装料排期的要求尚不明显,然而在乏燃料多机组多式联运时,装料排期计划的合理性尤为重要。
基于乏燃料多式联运单批次运输10个货包,以及多核电基地、多台机组和多个作业面同步装料等状况,通过统筹考虑各核电站乏燃料的外运紧迫性,并根据后处理设施的能力与容器资源进行动态调度,以实现乏燃料处理能力的进一步提升。
高级计划排程(Advanced Planning and Scheduling,APS)理论是对实际业务逻辑进行抽象建模,以实现对计划的制定与调度。文献[1]报道,刘海江等研究APS与传统能力需求计划(Capacity Requirement Planning,CRP)的能力需求分析比较,发现APS具有整体规划、计划优化和实时性这三个技术特点;Rudber分析了APS的实施对钢铁加工公司战术计划水平的影响[2];Romero研究了批量化学加工行业中和财务管理有关的计划和排程问题[3];张腾飞等利用APS系统解决了车间作业调度问题,重点是运用改进遗传算法来解决经典的作业调度和柔性作业调度问题,并验证了算法的性能[4];吴雁等提出了一种基于制造执行系统(ManufacturingExecution System,MES)的机加高级计划排程的应用框架,并通过实际的应用案例来验证该框架[5];肖牧山等提出了基于约束理论(Theory of Constraints,TOC)和鼓-缓冲 -绳(Drum-Buffer-Rope,DBR)模型的APS系统与企业资源计划(Enterprise Resource Planning,ERP)集成的解决方案,并给出了APS与ERP集成的潜在问题和可行方案[6];沈洁锋等对乏燃料的管理方式以及我国乏燃料管理的现状进行了分析讨论[9];李晓娟等利用信息技术、物联网和大数据等技术手段,通过提升设备智能化水平完善运输保障,搭建智能化监管平台和应急响应平台以实现全过程的可视化监管和快速反应上报等,保障危险品的安全运输[7]。涉及乏燃料调度体系的研究鲜少,故刘群等认为需要建立乏燃料调度体系,以实现各环节的高效调度与统筹协调[8]。
综上所述,在APS的应用和研究方面,APS理论多应用于生产制造领域,尚未用于乏燃料运输领域。本文根据乏燃料运输计划的特点,基于运输计划的业务逻辑,应用APS理论,建立了混合整数规划模型,并兼顾模型的规模与未来的拓展性,设计了一种启发式算法实现加快模型求解过程。
1 基于资源约束的APS模型
在单次运输计划中,装料环节耗时长,在整个周期中占比大,且各机组的装料时间窗不同,故装料排期计划不同导致装料完工时间不同。装料环节按各电站内其机组的外运紧迫性,以及各机组的装料时间窗、容器数量上限和各后处理厂的卸料时间窗等约束条件,对多台机组进行空容器分配,并兼顾单个货包装载高燃耗组件至卸料全过程低于6个月的前提下,以期使装料完工时间最短。
1.1 模型假设
(1)各机组有多个不可装料时间窗;
(2)不考虑总成本变化;
(3)不考虑电站间空闲作业面调度分配;
(4)不考虑装/卸空容器时间;
(5)所有容器的容量相同;
(6)单个容器装/卸料时间为11/15 d;
(7)换装、海运和铁运时间均为固定标准时间;
(8)每个电站最少配置1套作业面(1辆公路运输车和装/卸料专业设备等);
(9)装料无抢占性,即不允许任意作业面的装料插入另一作业面的装料过程中;
(10)各机组装料任务必须连续作业。
1.2 参数和变量
本文涉及的参数和符号如表1所示。

表1 符号说明Table 1 Parameter description
1.3 数学模型
乏燃料装料排期计划涉及装料任务完成时间优先和外运紧迫性优先两个目标。
装料任务完成时间目标:

外运紧迫性目标:

其中,wij=Cij/Lij
将不同目标归一化后采用加权的方法求解。时间目标是求解单个作业面的最大完工时间,外运紧迫性目标是求解所有机组外运紧迫性的最高值,因此将单目标设为最大值函数。考虑到实际场景中两者的相对重要程度,将早期的时间设置更高的权重,使装料计划被提前执行,以节省总体装料时间,降低计划的完成时间。确定的目标函数如式(3)所示。
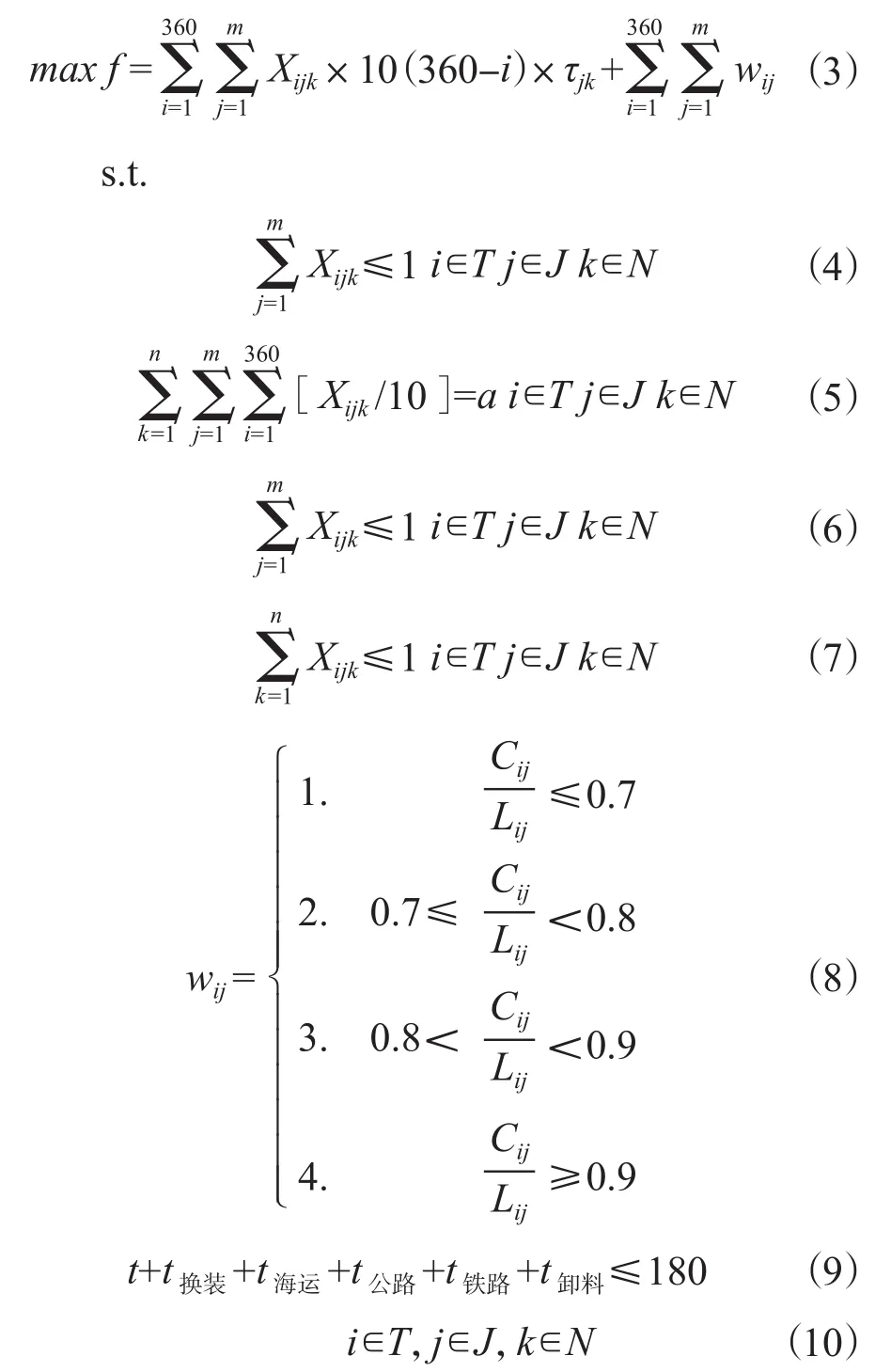
其中:
公式(1)为时间目标,即最小化最大完工时间,指从第一个机组装料开始时间到最后一个机组卸料完成所耗时间的最小化;
公式(2)为外运紧迫性优化目标,即优先到外运紧迫性高的机组装料;
公式(3)为多目标归一化后的目标函数,即在满足尽早开始装料时间的前提下,外运紧迫性高的机组优先开始装料;
公式(4)表示每个机组每次分配容器上限,即第j个机组最多分配μj个容器次;
公式(5)表示总分配容器次数量上限,即各机组分配容器次等于目前拥有的容器次;
公式(6)表示作业面数量上限,即同一时刻i、同一作业面k下,只能存在一个机组j装料;
公式(7)表示单机组不可同时装多个容器,即同一时刻i、同一机组j下,只能存在一个作业面k进行装料;
公式(8)表示外运紧迫性约束,根据各机组存量占比将外运紧迫性进行分级处理;
公式(9)表示总运输完成时间满足时长约束;
公式(10)为变量取值约束。
2 算法设计
整个运输计划的装料排期问题本质上属于车辆路径问题(Vehicle Routing Problem,VRP),而VRP是典型的非确定性多项式难题(nondeterministic polynomial hard,NP-hard),故装料排期计划也属于NP-hard问题。
本文建立的模型中既有连续变量又有整数变量,为混合整数规划模型。从可拓展可推广的角度出发,设计基于优先规则的启发式算法来求解该问题。其求解流程如图1所示。
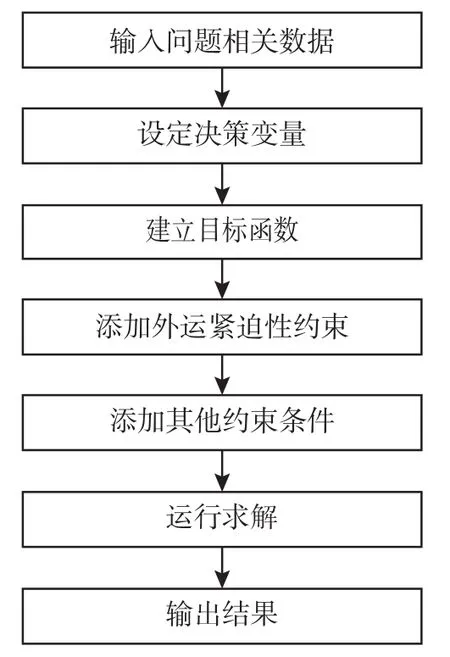
图1 求解流程Table 1 Solve loop
首先根据单次计划需要处理的乏燃料数量,确定需要使用的总空容器的数量;然后基于一定的分配策略将空容器分配到各机组,及时运走对应机组燃料池中的乏燃料,使得各机组能够稳定安全运行。
当单次计划需要处理的乏燃料数量不同时,需要使用的空容器数量也不同。对于分配策略的选择,既可依各机组外运紧迫性的大小排序,亦可任意分配,以寻找单次运输计划用时最短的分配方案,并要满足各机组紧迫性的上下限。
根据紧迫性大小排序进行分配,人工干预的程度较大,找到的方案与最优解的距离较大。如果任意分配,当需要使用的空容器数量比较多时,计算成本较大,需要由代码的执行效率决定。本文采取上述二者之间折中的方案,具体步骤如下:
Step1:输入数据和相关参数。
Step2:随机生成各组件状态信息,根据组件状态分析各机组组件的最小冷却时间,以及在装料计划开始时间时是否完成冷却。
Step3:基于各组件完成冷却时间确定计划开始时间时各机组的最大可外运量。
Step4:加入各机组的不可装料时间窗和后处理厂的卸料时间窗。
Step5:创建模型,加入外运紧迫性权重,建立多目标归一化的总运输时间最小化目标函数。
Step6:添加各项约束条件。
Step7:设置解池参数,允许输出多个满足时长约束的分配方案。
Step8:执行算法。每确定一个机组的容器分配顺序和数量,各机组外运紧迫性也会随之进行更新迭代,直至将空容器全部分配完毕。
Step9:输出结果。输出单次运输计划总运输时间、货包视角的装/卸料开始及结束时间、各机组分配的容器数以及多个具体可行方案。
3 算例验证
3.1 算例信息
以2个电站、12台机组为例,设定10台容器、3个作业面和2个后处理厂,装料开始时间为2022年11月11日。各机组池中组件状态信息见表2,各机组与后处理厂的不可装卸料时间窗信息分别见表3和表4,各机组的外运紧迫性见表5。

表2 池中组件状态信息Table 2 Spent fuel assembly status
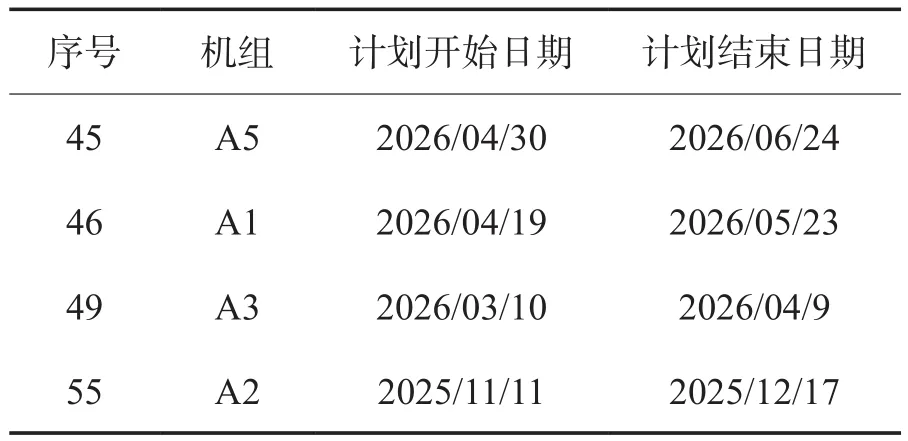
表3 机组不可装料时间窗Table 3 Unit unavailable charge date
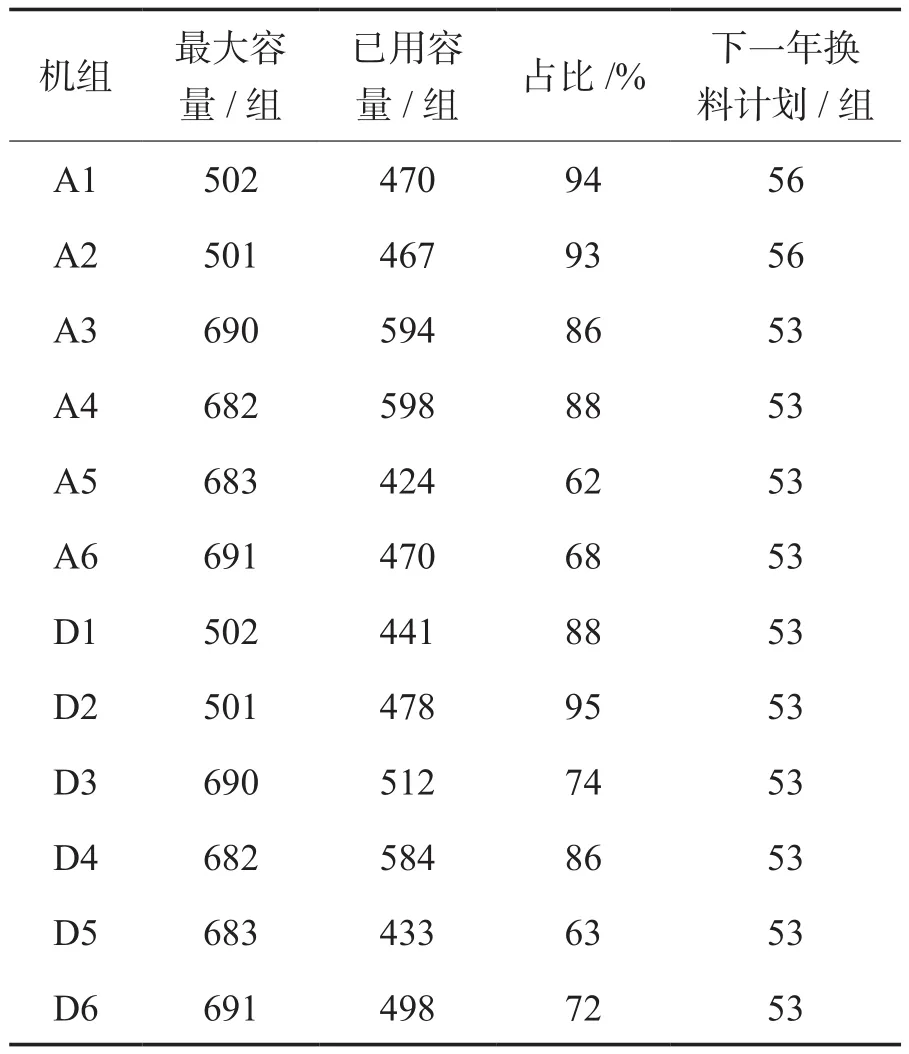
表5 机组外运紧迫性Table 5 Unit transport urgency
首先根据池中组件状态信息,结合乏燃料最小冷却时间表,确定每个机组最多可外运的组件数,以确定各机组可分配的容器上限。
其次根据各机组的外运紧迫性和不可外运时间窗,将既有的容器分配给各机组,得到若干个可行且在时间上最优的方案。
最后根据运输各子环节预设时间,推导每个容器开始装料与装料完成时间,开始卸料与卸料完成时间,并分析得到的方案是否符合从装料开始到卸料结束的时间约束。
算法结果最终输出多个满足约束条件的可行方案。以第一个输出方案为例,求解结果如表6所示,A电站内A1机组分配3个容器,A5机组分配2个容器,D电站内D1机组分配3个容器,D4机组分配2个容器,单次运输计划总运输时长为137天,各容器运输时间均满足180天约束。此外,算法将输出具体可行方案运输批次及时间节点,如表7所示,第一批次装料计划分配给A1、A3、D1各1台容器,第二批次分配给A3、D1、D4各1台容器,第三批次分配给A1、D1、D4各1台容器,第四批次分配给A1机组1台容器。
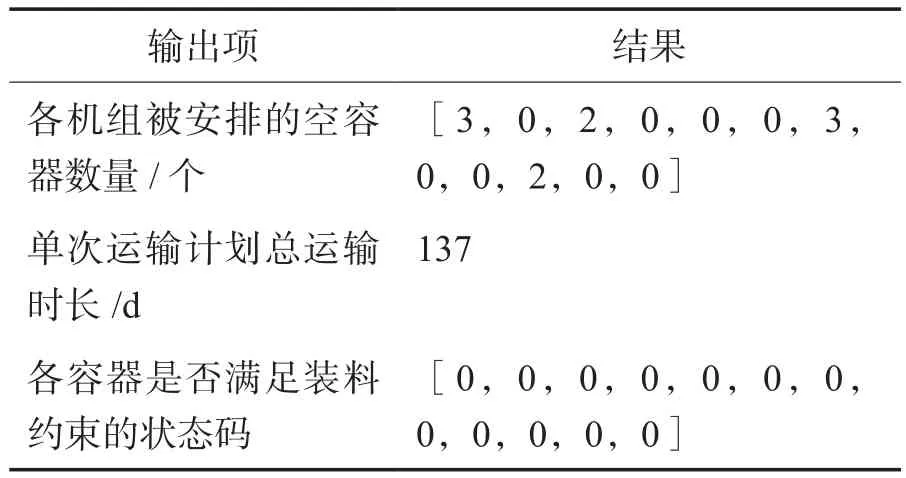
表6 第1种方案求解结果Table 6 Plan 1 solution result

表7 第1种方案的时间约束判定Table 7 Plan 1 time constraint determination
3.2 仿真结果
在乏燃料实际单次运输计划中存在许多不确定性,造成优化方法应用到实际运输过程上的局限性。离散仿真系统具有很好的模拟实际运输过程不确定情况的能力,但不具备良好的优化能力。通过仿真软件中搭建乏燃料单次运输计划模型与算法的结果相结合的方式,验证装料排期方案的合理性。建立仿真模型以模拟乏燃料单次运输计划的运输过程,将算法所需数据输入所建混合整数规划模型中,运用启发式算法求解出装料排期方案,将优化方案输入仿真模型中推演,与人工排期方案的仿真推演结果作对比,验证算法输出方案的可执行性与优化性。
由表8可知,人工排期方案中A3机组分配容器数过多,而算法优化计划的容器分配更为均匀,理论上机组不会出现或较少出现装料排队现象。

表8 装料计划容器分配数量对比Table 8 Charge container allocation comparison
通过仿真系统分别输入人工排期计划、算法优化计划的数据进行流程模拟,对比乏燃料单次运输计划各环节所需时长及各容器的时间信息,见表9。
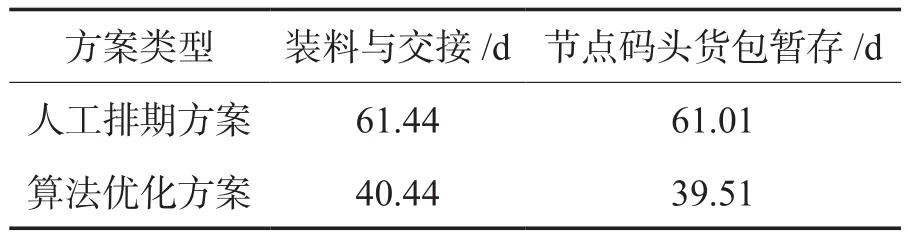
表9 各环节所需时间对比Table 9 link time consumption comparison
从表9可知,算法优化方案中的“装料与交接模块”时长约40 d,较人工排期方案中的“装料与交接模块”时长约61 d节约21 d,同时受装料时间影响,算法优化方案较人工排期方案的“节点码头货包暂存模块”时长节约22 d左右。
由表10可知,人工排期方案和算法优化方案均能满足时间约束,但算法优化计划中各货包占用的时长短于初始装料计划,使得单次运输计划更具可执行性。
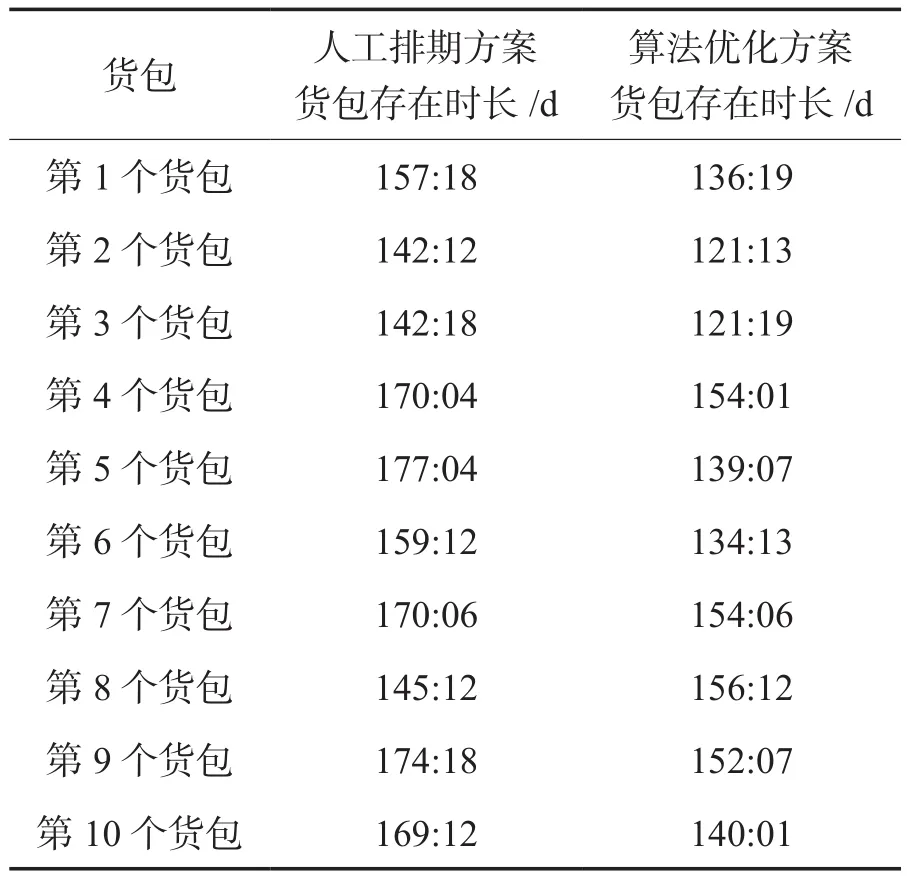
表10 货包时间信息对比Table 10 Package existence time comparison
综合上述容器分配数量、各环节所需时间和货包时间3个方面的对比,表明提出的模型在运输计划装料排期环节的优化方案,有效缩短了整个装料环节时间,提高了运输计划的可执行性。
4 结束语
本文针对乏燃料单次运输计划中多约束的装料排期问题,以最小化运输时间为目标建立了优化模型,利用基于优先规则的启发式算法求解该混合整数规划模型。在算例分析中,分析多约束条件对装料排期的影响,结果表明该优化方案推演的运输时长优于人工排期方案,不仅节省大量人力,还为乏燃料单次运输计划的制订提供实用价值。
