一种高效太阳能储热水箱温度分层特性的实验研究

于伟洋，石 岩，陶 进，张俊男

（1：吉林建筑大学市政与环境工程学院，吉林 长春 130118；2：吉林建筑科技学院,吉林 长春 130114）

0 引言

太阳能储热水箱是太阳能供暖系统的重要组成部分，一方面能够储存热量，另一方面可协调源侧和负荷侧保持合理水温，以保证供暖需求[1]。在储热水箱内部，由于不同温度的流体之间存在密度差异，使得高温流体上升，低温流体下降，从而形成了温度分层现象。储热水箱中的温度分层现象对提高水箱的热性能具有显著影响，温度分层现象越明显，储热水箱储存的可用能越多，同时可降低集热器的进口温度，从而提高整个太阳能供暖系统的效率[2]。

目前各国学者对储热水箱温度分层特性的研究主要集中在储热水箱内部结构（高径比、入口位置和尺寸、箱体形式）和运行工况对分层的影响[3]。韩延民等[1]设计了一种新型结构的太阳能储热水箱，并对其温度分层特性进行了实验研究，研究认为温度梯度或斜温层是维持稳定温度分层的关键。YAICI等[4]通过软件模拟，对储热水箱的分层性能的影响因素进行研究，分析了高径比、进水与水箱中水之间的温差及入口流量等因素的影响。另外，有研究学者提出了一些参数来评价储热水箱温度分层的效果。

综合国内外研究进展，本文主要从储热水箱在垂直方向不同高度测点的温度变化曲线入手，分析了整个储热过程的温度分层特性，同时对不同流量下的水箱Str函数和MIX函数的变化情况进行了计算分析。

1 实验系统的搭建

1.1 新型储热水箱结构介绍

新型管壳式储热水箱，箱体尺寸为长700 mm，宽700 mm，高1 500 mm，最大蓄水容积为0.7 m3，水箱入口距底部50 mm，入口出口垂直间距1 200 mm。箱体内部主要由带有螺旋翅片的U型换热盘管组成,盘管外径19 mm，壁厚1 mm，两管中心间距90 mm，水平直管长500 mm，两管外壁之间的间距为109 mm。图1为新型储热水箱内部结构图。箱体的外部覆盖了50 mm的聚乙烯泡沫用于与环境隔热保温，在箱体顶部留有1个小孔防止水箱由于热胀冷缩而引起箱体变形，同时也用于连接所有的热电偶到电脑以读取数据。

图1 储热水箱内部结构

1.2 实验系统介绍

本实验系统主要由太阳能集热器、带有电加热的稳压水箱、新型储热水箱、循环水泵、阀门、电磁流量计及数据采集系统组成，实验系统原理如图2所示。

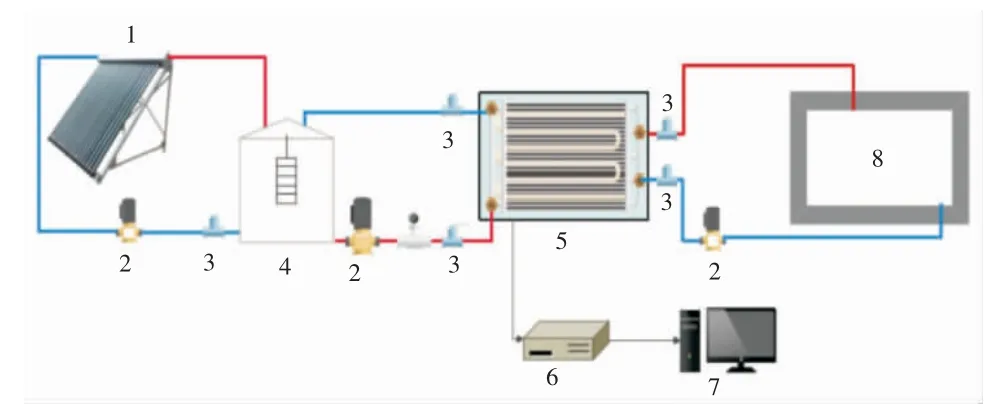
图2 实验系统原理

通过阀门和水泵的开启来实现太阳能集热、储热水箱储热、储热水箱放热3种循环方式。在储热水箱内部不同高度布置9个温度传感器PT100，每个传感器垂直间距为150 mm,用于记录不同高度测点的温度变化。入口流量通过调节阀门来控制,同时由电磁流量计进行记录。实验的主要设备参数见表1。

表1 设备技术参数

1.3 实验流程

本实验可分为预热、储热、静置和放热4个过程，首先当太阳能辐射强度较高时，打开太阳能集热循环，进行水箱储热；当太阳能辐射强度过低时，打开恒温水箱中的加热装置，当达到储热要求的温度时停止加热。之后打开循环水泵M2以70℃入口温度，0.8 m3/h，1.0 m3/h，1.2 m3/h这3种不同入口流量对储热水箱进行储热，当储热水箱出口温度在10 min内变化≤1℃时，认为储热过程结束。之后进行静置，当储热水箱内部各测点温度趋于稳定时，进行放热过程。

2 数据分析

2.1 温度变化曲线

图3表示入口温度70℃，入口流量0.8 m3/h，1.0 m3/h，1.2 m3/h这3种运行工况下储热水箱内部不同高度上测点温度的变化。

由图3可以看出不同测点在储热过程中开始温度上升速率较快，之后逐渐减少直到不再发生变化，并且在不同高度上出现明显的温度分层现象。说明开始时水箱内部冷热流体扰动较为强烈，温度急剧上升，之后温度上升减缓,并且逐渐出现温度分层。同时，当入口流量在0.8 m3/h，1.0 m3/h，1.2 m3/h这3种工况下，储热水箱完成储热的时间为16 800 s，15 600 s，14 100 s，储热完成时水箱垂直方向不同测点的最大温差分别为10.52℃，12.4℃，9.76℃。说明提高入口流量能够明显缩短水箱储热时间，在一定范围内入口流量越高,温度分层效果越好，但超过一定阈值时分层效果会减弱。这是由于提高入口流量，能够提高换热管内流体的流速，使流体从层流提高至紊流状态，流体传热更快，水箱内部温升更快。同时增加流量能够提高流体温升速率，使温度分层效果更好，但流量过大则水箱内部冷热流体的扰动过于剧烈，掺混严重，温度分层效果则会减弱。

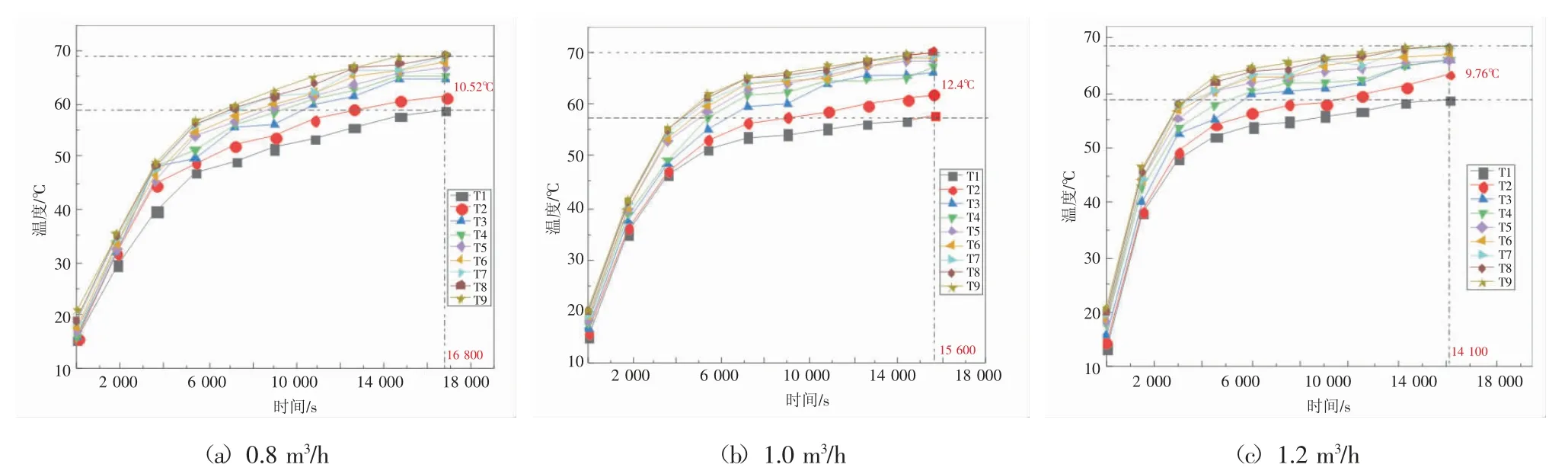
图3 不同入口流量的各测点温度变化

为了分析不同入口流量在不同时刻水箱储热的变化情况，引入无量纲时间[5]，其定义为：

式（1）中：t为从开始储热到储热结束的时间，min；T水箱内的水置换一遍所需的时间，min。

同时为了消除水箱内部不同测点初始温度的差异，引入无量纲温度T*[6]，其定义为：

式（2）中：T为水箱垂直方向不同测点温度，Tstart水箱内部测点初始温度，Tinter为水箱入口温度，℃。

本文取无量纲时间t*=0.25，0.5，0.7表示水箱储热初期、中期、末期，经过计算可以看出在水箱储热初期，由于冷热流体温差较大，各测点都在大量吸热，因此水箱内部温度分层现象不明显；在储热中期，水箱内部不同高度的测点开始出现温差，说明水箱出现温度分层现象；在储热后期，各测点的温差最大，说明此时的水箱温度分层最为明显。

2.2 不同流量下的Str函数的变化

SEARA等[7]在文章中提出Str函数。Str函数是另一个表征蓄热水箱温度分层性能的指标，它是1个随时间变化的值，表明某一时间温度梯度的平均值与整个进出水过程最大的温度梯度的平均值的比值，温度梯度主要是通过水箱各层温度测点获得的温度值计算而得到的。计算公式为：

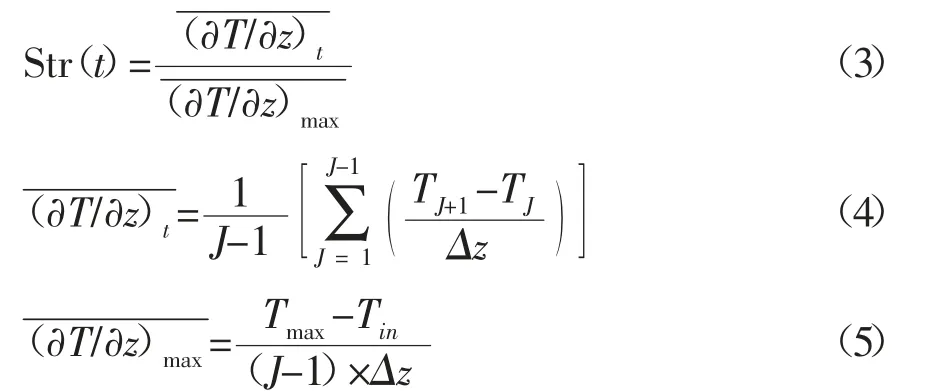
式（3）～（5）中：J为水箱分层数，个；Δz为每层分层高度，m；Tmax为某时刻水箱垂直方向的最高温度，Tin为水箱入口温度，℃。

以入口温度70℃，流量为0.8 m3/h，1.0 m3/h，1.2 m3/h这3种运行工况对水箱储热，计算不同入口流量下的水箱Str数随无量纲时间的变化，如图4所示。

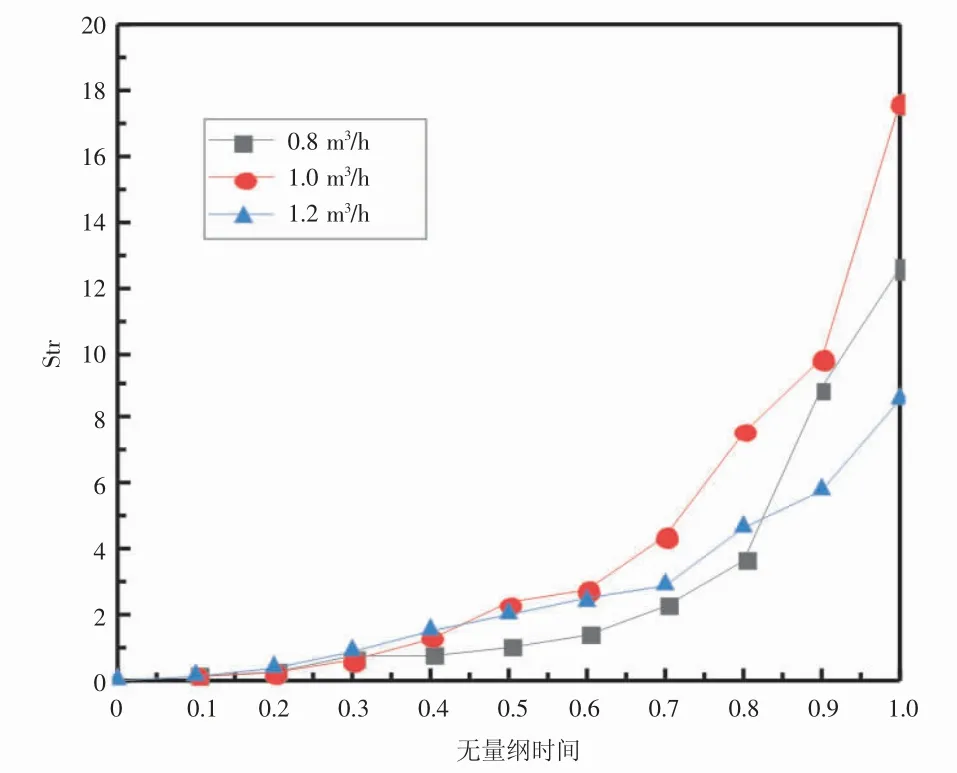
图4 不同入口流量的水箱Str函数变化

由图4可知，3种流量下的Str函数开始较小并且增加比较缓慢，说明开始时水箱温度分层现象不够明显。在储热后期，Str函数急剧上升，说明水箱出现温度分层现象，并且温度分层现象越加明显，直至水箱储热完成。同时当水箱储热完成时，流量0.8 m3/h，1.0 m3/h，1.2 m3/h的 最 大Str函 数 分 别 为12.6，17.61，8.56。流量为1.0 m3/h的Str函数最大，水箱温度分层最明显。

2.3 不同流量下的MIX函数的变化

丹麦学者ANDERSEN等[8]在论文中提出水箱的混合函数MIX，定义为：将水箱分为N个体积大小相同V的水平层，每层的能量为Mi，整个水箱总能量为M。其计算公式为：

式（6）～（7）中：ρi为水箱每一层工质的密度，kg/m3；ci为水箱每一层工质的比热容，J/（kg·℃)；Ti为水箱入口温度与每一层工质温度的温差，℃；yi为水箱每一层中心距水箱底部的垂直高度，m。

故定义MIX为：

式（8）中：Mstr为完美水箱的M值，Mexp为水箱实际的M值，Mmix为完全混合水箱的M值。MIX函数是一个介于0～1之间的值。MIX=1，表明水箱完全混合；MIX=0，表明水箱完全分层。

在实验中，可以测出每一水平层的平均温度，计算出每一层的能量，进而计算出整个水箱的能量。对于完全混合水箱时，水箱具有相同的平均温度；对于完全分层水，计算时可认为将水箱分为2个部分，高温部分为入口温度，低温部分为水箱平均温度。

图5为3种流量下水箱的MIX函数随无量纲时间的变化。

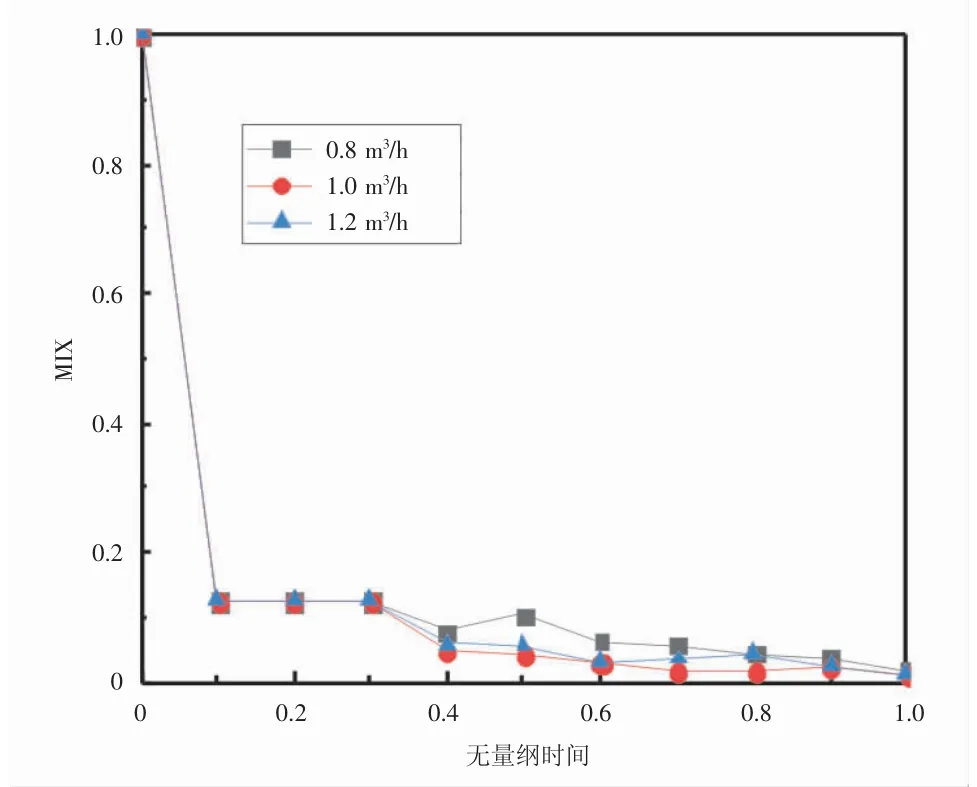
图5 不同入口流量的水箱MIX函数变化

由图5可知，3种流量下的MIX函数都呈现下降的趋势，在无量纲时间为0～0.1时，3组流量的MIX函数急剧下降，说明水箱开始出现温度分层。在无量纲时间为0.1～0.3时，3组流量的MIX函数变化不明显均＞0.1，说明该时间段分层不明显。在无量纲时间为0.3～1时，3组流量的MIX函数逐渐下降，且均在0.1以下，说明水箱内的温度分层逐渐接近完美分层。蓄热结束时，3种流量的MIX函数最小此时温度分层最为明显。同时，在无量纲时间0.3～1时，流量为1.0 m3/h流量下的MIX函数比0.8 m3/h和1.2 m3/h流量下MIX函数略小，例如当无量纲时间为0.5时，1.0 m3/h下的水箱MIX函数为0.046，比0.8 m3/h下的MIX函数低41%，比1.0 m3/h下的MIX函数低21%，说明流量为1.0 m3/h下的水箱分层效果最好。MIX函数的实验结论和Str函数分析得出的结论基本相符。

3 结论

本文设计了一种新型的太阳能储热水箱，通过实验对水箱内部的温度分层进行了分析，可以得出以下结论。

1）通过对水箱内部垂直方向的温度变化曲线可以得出，各测点的温升速率逐渐减缓，流量越大测点温升越快储热完成时间越短。同时在水箱储热无量纲时间的中后期出现温度分层现象，并且在储热完成时温度分层现象最明显。

2）在相同的无量纲时间内，不同入口流量对储热水箱的温度分层有明显的影响，入口流量1.0 m3/h的水箱温度分层效果最好，储热过程中的最大温差能达到12.4℃。

3）对不同流量下的水箱Str函数和MIX函数进行了计算，计算结果表明在无量纲时间内，储热水箱的Str函数在储热初期较小，中后期急剧增大，在储热结束时最大；储热水箱的MIX函数在储热初期较大，中后期急剧降低，在储热结束时最小，说明储热水箱在中后期出现温度分层并且在储热结束时分层效果最好。同时在入口流量为1.0 m3/h的水箱Str函数最大，MIX函数最小，水箱温度分层效果最好。