桥面纵坡对小半径曲线桥铺装层受力的影响分析

罗建群 陶雅乐

(1.招商局公路信息技术(重庆)有限公司 重庆 400067; 2.西南交通大学物理科学与技术学院 成都 610031)

桥面铺装层作为桥梁的重要组成部分，是铺设在钢桥面板上并且直接与外荷载接触，在分散荷载及保证行车安全等方面起决定性作用[1-2]。由于钢桥面刚度较小，变形较大，铺装层受力复杂，容易产生车辙、推移变形等损坏[3]。铺装层的损坏是导致钢桥面板结构破坏的重要原因，为提高钢桥面工作性能，众多学者从铺装层受力、变形等方面开展了大量研究工作。Chen等[4]采用多尺度评价方法总结桥面铺装裂缝分布规律，比较了传统模型和多尺度模型的优缺点，验证了将多尺度模型应用于桥面铺装的可行性；Cheng等[5]通过数值模拟研究了周期荷载和移动荷载作用下桥面铺装的力学响应，并且通过现场试验对模拟结果进行验证。Wang等[6]采用静态和动态相结合的方法对跨海大桥铺面进行现场试验研究，研究了车辆行驶速度和荷载距离对桥面铺装的力学响应，对铺装层厚度和模量提出合理建议。为满足受地形、用地等限制下的交通需要，建造纵坡大、半径小的曲线桥是必要的，在曲线桥梁结构的设计中，应该对整个结构进行全面的整体的空间受力计算分析。除了横向力外，还必须对其在承受纵向弯曲、扭转和翘曲作用下，结合自重、预应力和汽车活载等荷载进行详细的受力分析，充分考虑其结构的空间受力特点，才能得到安全可靠的结构设计。铺装层的加入会使桥体的自重增加，受力分析更加复杂，铺装层的材料、铺装厚度均会对桥梁整体的结构产生影响。相比于直道桥，曲线桥铺装层受力更为不利，寿命更短，更容易遭受损坏，所以要求铺装层具有更高的高温稳定性和界面安全性[7]；另，Lan W和Ma H[8-9]等指出由于曲线桥几何形状复杂，桥面铺装上的轮胎荷载与曲率半径、纵坡、车速，以及车轮荷载有关。因此，本文以某大温差地区小半径曲线桥为例，研究分析温度、动荷载、温-荷耦合等不同荷载工况下的铺装层受力情况，以期为大温差地区小半径曲线桥铺装层优化设计提供理论支持。

1 计算模型与参数

1.1 有限元模型

采用Abaqus有限元软件建立3跨连续梁曲线桥全桥模型，全桥长148.89 m，半径为62.69 m。主梁和桥面铺装均用实体单元模拟，考虑钢箱梁为弹性连接，全跨梁采用单箱双室钢箱梁，钢箱梁材料为Q355。桥面铺装采用双层SMA-13改性沥青混凝土，铺装表层层厚4 cm，铺装下层层厚3 cm。桥面铺装结构层、网格图、荷载图见图1。建模时做如下假定:①沥青混合料铺装层是连续的、均匀的、各向同性的;②铺装层与钢箱梁的层间接触是完全连续的，采用tie连接;③钢箱梁和铺装层的自重计算在内。

图1 有限元模型示意图

1.2 材料及气象参数

用Abaqus有限元分析软件对曲线桥全桥模型进行计算，采用大温差地区7月的大气温度实测数据，使用用户子程序FILM、DFLUX，考虑在太阳辐射、路面的有效辐射、气温，以及对流热交换影响的作用下，模拟以24 h为1个周期的连续3个周期变温条件下曲线桥温度场。桥面铺装层温度场传热见图2，相关气象参数与材料热物性参数见表1、表2。

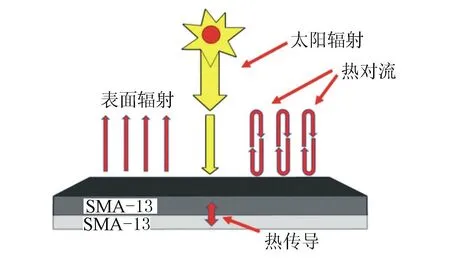
图2 桥面铺装温度场传热示意图

表1 7月气候参数

表2 材料热物理参数

温度应力分析采用Abaqus的热力耦合方法。沥青混合料SMA-13使用广义Maxwell黏弹性本构模型进行模拟，采用广义Prony级数进行拟合，时温等效原理采用WLF方程拟合，Q355材料采用线弹性拟合。WLF拟合公式如下。

(1)

式中：θ0为参考温度；取20 ℃，C1和C2为试验确定系数。

材料热力学参数见表3～表6，其中Q355线膨胀系数受温度影响忽略不计。

表3 主要材料材料力学参数

表4 黏弹性材料Prony级数

表5 黏弹性材料WLF方程参数

表6 路面结构材料线膨胀系数

1.3 移动荷载作用形式

根据我国现行JTG D50-2017 《公路沥青路面设计规范》，路面设计采用双轮组单轴载100 kN作为标准载荷，表示为BZZ-100。通过Abaqus子程序DLOAD及UTRACLOUD实现移动荷载的加载，将实际计算中的荷载作用面积简化为矩形，见图3、图4，其中接地压力取0.7 MPa。动荷载示意图见图5，其中深色区域为移动荷载行驶轨迹。

图3 荷载模型

图4 单轴双轮荷载(单位：cm)

2 计算方案设计

本研究探讨了不同荷载工况下曲线桥的受力影响，按规范JTG B01-2014 《公路工程技术标准》相关要求进行纵坡取值，分析不同工况下纵坡(4.22%，5.22%，6.22%，7.22%)对桥面铺装层受力的影响。

2.1 温度场

初始设置曲线桥横坡为3%，纵坡为4.22%。为减少误差，采用3个周期循环作业的方式，其中1个周期为24 h。

在温度场模型中，分别提取曲线桥不同铺装层温度最大值。待曲线桥内部的温度场达到稳定后，在后续研究中提取稳定后的第3个周期铺装层温度场结果进行分析。

2.2 温度应力

在前文曲线桥温度场模型基础上，加入相关材料的力学参数建立温度应力计算的模型，导入温度场计算结果，计算得出曲线桥不同铺装层x、y方向温度应力。

2.3 动荷载

在纵向最不利荷位定为曲线桥跨中中心处基础上，采用4种不同的动荷载加载方式，分析并确定曲线桥横向最不利荷位。

横坡设为3%，改变曲线桥纵坡，分别设置纵坡为4.22%，5.22%，6.22%，7.22%，在横向最不利位置施加动荷载，分别计算得到各纵坡下铺装层沿x、y方向的拉应力和最大剪应力。

2.4 温-荷耦合

选取温度场分析中最不利温度时刻导入温-荷耦合计算模型中，分别计算上述各纵坡下不同铺装层的拉应力和最大剪应力。

3 结果与分析

3.1 温度作用下铺装层受力特性

3.1.1温度场分析

设曲线桥横坡为3%，纵坡为4.22%，模拟72 h桥面不同铺装层最大温度，见图6。

图6 3个周期下桥面铺装结构温度变化(i=4.22%)

通过改变曲线桥纵坡，分别设置纵坡为4.22%，5.22%，6.22%，7.22%，相应地提取第3个周期不同铺装层温度最大值见图7。

图7 不同纵坡坡度下铺装层温度场分布

由图7可知，纵坡变化对铺装层温度变化几乎无影响。同时，铺装表层温度和大气气温同时在15：00达到1 d内最高温度，但两者最大温差达17 ℃。对于铺装下层，纵坡取值为6.22%时，铺装层达到1 d内温度最大值29.9 ℃；特别地，铺装下层达到最高温度时间较铺装表层推后了1 h。这是因为日出之后太阳辐射逐渐增加，铺装层不断吸收热量，铺装层表面温度逐渐增加，同时铺装层表面对下结构层有热传导作用，即离铺装层表面越近的结构层温度上升就越快，越早达到温度最大值，而离铺装层表面越远的结构层温度上升越慢，越晚达到温度最大值。

3.1.2温度应力分析

选取3个具有代表性的时刻(00:00，06:00，11:00)的温度应力作为铺装层结构受力分析的典型温度应力。

图8 不同纵坡坡度下铺装层温度应力σx分布

图9 不同纵坡坡度下铺装层温度应力σy分布

由图8、图9可知：

①随着环境温度的变化，铺装层应力也不断发生变化。由于铺装表层直接接触外界环境，其1 d内的温度应力变化幅值明显大于铺装下层；②对于铺装表层：在00:00，当纵坡为6.22%时，达到σx最大值2.9 MPa；同一时刻，当纵坡为4.22%时，达到σy最大值2.96 MPa；③对于铺装下层，图示3个时刻，不同纵坡对铺装下层σx、σy影响均不显著。

综上，σy>σx，且路线纵坡变化对σy的影响更显著，说明铺装层更容易产生纵向开裂。另外，对于铺装层纵向温度应力σy，随纵坡的增加而减少，因此仅考虑温度场作用，建议该曲线桥纵坡选取7.22%为宜。

3.2 移动荷载作用下铺装层受力特性

3.2.1最不利荷位的确定

采用4种不同的动荷载加载方式见图10，分析并确定曲线桥横向最不利荷位，计算结果见表7。

图10 横截面动荷载加载位置示意图

表7 不同荷位下铺装层力学计算指标

由表7可知，作用于纵隔板上的荷位2、3拉应力远大于远离纵隔板位置的荷位1、4，这是由正交异性板的力学性质所决定的。由于钢箱梁承受的刚度不均匀，纵隔板处刚度比较大，动荷载作用在纵隔板附近表现为负弯矩，铺装层顶随之产生负弯矩，加之动荷载的反复作用，容易在纵隔板上方形成疲劳裂缝。当动荷载加载位置为荷位2时，铺装层的最大拉应力、最大拉应变、最大剪应力达到最大值，故以荷位2作为曲线桥动荷载加载的横向最不利荷位。

3.2.2动荷载作用下铺装层受力分析

1) 铺装层拉应力。各纵坡下铺装层不同时刻沿x方向拉应力σx和沿y方向拉应力σy见图11、图12。由图11、图12可知：

①在相同纵坡以及荷载参数作用下，铺装表层σx、σy均大于铺装下层，在移动荷载单独作用时铺装表层更容易产生受拉破坏；对于不同纵坡下铺装表层，σx随着纵坡的增加不断增加，当纵坡为7.22%时，在0时刻取得最大值4.0 MPa，相反，σy随着纵坡的增加不断减小，当纵坡为4.22%时，在0时刻取得最大值4.3 MPa；对于不同纵坡铺装下层，不同纵坡对σx、σy影响均不显著；②根据不同纵坡和应力的拟合公式，拟合曲线斜率的绝对值越大，应力值对纵坡变化越敏感。从图示可以看出，铺装表层σy对纵坡敏感性大于σx，纵坡对σy影响更显著。不同纵坡下σx<σy，所以在动荷载作用下，铺装层表面容易产生纵向裂缝。

图11 不同纵坡坡度下铺装层x方向拉应力

图12 不同纵坡坡度下铺装层y方向拉应力

2) 铺装层剪应力。各纵坡下铺装层不同时刻最大剪应力见图13。

图13 不同纵坡坡度下铺装层最大剪应力τ

由图13可知：

①铺装下层τ大于铺装表层；在0时刻，当纵坡为7.22%时，在铺装下层取得τ最大值5.3 MPa；不同纵坡对铺装表层τ影响不显著，但对铺装下层τ影响显著；②根据不同纵坡和剪应力的拟合公式，铺装下层τ和纵坡呈正相关性，且铺装下层τ对纵坡敏感性大于铺装表层，应提高铺装下层抗剪能力。

因此，在动荷载作用下，为提高铺装层抗横纵向开裂以及抗剪性能，建议曲线桥选取纵坡为6.22%为宜。

3.3 温-荷耦合作用下铺装层受力分析

3.3.1铺装层拉应力分析

各纵坡下铺装层不同时刻沿x方向拉应力σx和沿y方向拉应力σy见图14、图15。

图14 不同纵坡坡度下铺装层沿x方向的拉应力

图15 不同纵坡坡度下铺装层沿y方向的拉应力

由图14和图15可知：

①在相同荷载参数及时温状况作用下，铺装下层σx、σy均大于铺装表层；②对于不同纵坡铺装表层，σx随着纵坡的增加不断增加，当纵坡为7.22%时，在0时刻取得最大值1.9 MPa；不同纵坡对σy影响不显著；③对于不同纵坡铺装下层，当纵坡为5.22%，在50时刻取得σx最大值2.1 MPa，在相同纵坡和时刻，取得σy最大值2.12 MPa；④当纵坡≤5.22%，随纵坡增加，铺装下层σx、σy增大，相反地，当纵坡>5.22%，随纵坡增加，铺装下层σx、σy减小。说明当坡度≤5.22%时，温度是影响铺装层拉应力的主要因素；当坡度>5.22%时，纵坡是影响铺装层拉应力的主要因素，且纵坡的增加对铺装层拉应力起到削减作用；⑤根据图示不同纵坡和拉应力的拟合公式，铺装层σx对纵坡的敏感性大于σy，不同纵坡对σx影响显著。

3.3.2铺装层剪应力分析

各纵坡下铺装层最大剪应力见图16。

图16 不同纵坡坡度下铺装层最大剪应力τ

由图16可知：

1) 对于不同纵坡铺装表层，随纵坡增加，τ不断增加，当纵坡为7.22%时，在动荷载作用0时刻τ取得最大值2.7 MPa。

2) 对于不同纵坡铺装下层，纵坡≤6.22%时，随纵坡增加，τ减小；纵坡>6.22%时，随纵坡增加，τ增加，说明纵坡的增加对τ起增大作用；纵坡大于临界值6.22%时，纵坡对τ的影响会超越横向力和温度；当纵坡为7.22%时，在动荷载作用0时刻取得τ最大值3.2 MPa。

3) 根据不同纵坡和应力的拟合公式，铺装表层τ与纵坡呈正相关性，而铺装下层τ与纵坡呈负相关性，且前者数值对纵坡的影响更敏感。

在温-荷耦合作用下，为提高铺装层抗开裂和抗剪性能，建议曲线桥纵坡选取6.22%为宜。

综合对比图11～图16，、动荷载单独作用下铺装层最大拉应力和剪应力均大于温-荷耦合作用下对应应力，当纵坡为5.22%时，耦合作用下铺装层拉应力达到最大值2.1 MPa，相较于只考虑动荷载作用，拉应力减少40%，相似的，当纵坡为7.22%时，耦合作用下最大剪应力达到3.2 MPa，相较于只考虑动荷载作用，最大剪应力减少65%，故认为温-荷耦合作用对铺装层的受力起抑制作用，更有利于铺装层的受力。

不同工况下纵坡和应力的拟合公式见表8。

表8 不同工况下的拟合公式

由表8可见，在动荷载工况下，不同纵坡对最不利应力值影响最大，其次是温-荷耦合工况，温度场的影响最小。这表明在研究不同纵坡下桥面铺装层的稳定性中，主要考虑动荷载的影响，温度可作次要因素进行分析。

4 结语

本研究基于雅康高速公路匝道桥铺装技术项目，为了满足现有建设空间的约束，本文曲线桥半径设定为固定值，采用三维有限元的方法研究了温度、动荷载、温-荷耦合等不同荷载工况下小半径曲线桥桥面沥青铺装层力学行为，探讨了不同工况下纵坡对桥面铺装层受力的影响。研究结果如下。

1) 仅考虑温度场作用时，铺装表层拉应力大于铺装下层；不同纵坡对铺装下层拉应力影响不显著；铺装层横向拉应力始终大于纵向拉应力，并且纵坡变化对σy影响显著，铺装层更容易产生纵向开裂；建议该工况下曲线桥纵坡选取7.22%为宜。

2) 仅考虑动荷载作用时，铺装表层更容易产生受拉破坏；随纵坡增加，铺装表层σx增大，相反地，随纵坡增加，σy减小；铺装表层σy对纵坡敏感性较大，并且纵坡对σy有显著性影响，易产生纵向裂缝；建议该工况下曲线桥选取纵坡为6.22%为宜。

3) 考虑温-荷耦合作用时，铺装下层是最不利受力位置；不同纵坡对铺装层σx影响显著，并且σx对纵坡敏感性较大；随纵坡增加，铺装表层拉应力和最大剪应力均增大；而对于铺装下层，当纵坡坡度≤5.22%，温度是影响铺装层拉应力的主要因素，而纵坡坡度>5.22%后，纵坡是影响铺装层拉应力的主要因素，且随纵坡的增加对铺装层拉应力起消减作用；相似的，当纵坡坡度>6.22%，纵坡是影响铺装层最大剪应力的主要因素，且随纵坡增加，对铺装层最大剪应力起消减作用；建议该工况下曲线桥纵坡取6.22%为宜。

4) 根据不同工况纵坡和应力的拟合公式，动荷载是影响最不利应力对纵坡敏感性的主要因素，在研究不同纵坡下桥面铺装层的稳定性时，动荷载可作重点分析；温-荷耦合作用会减少铺装层最不利应力对纵坡的敏感性。

5) 综合只考虑动荷载作用及温-荷耦合作用2种工况，温-荷耦合对铺装层的受力起抑制消减作用，更有利于铺装层的受力。