五种地下水埋深预测模型对比分析——以肇州县为例

张嗣路，李治军，于博文，王涛

（1.黑龙江大学水利电力学院，黑龙江哈尔滨 150080；2.黑龙江大学寒区地下水研究所，黑龙江哈尔滨 150080）

地下水动态变化是一个受自然条件与人类活动影响的复杂的水文过程，在时间序列上具有高度的滞后性与随机性。当地下水埋深持续增加，会造成地面沉降形成地下水漏斗；当地下水埋深变浅，会出现土壤次生盐渍化。因此，预测地下水埋深是区域水资源管理配置的重要基础，对于水资源的可持续利用和生态环境的保护至关重要［1］。传统地下水埋深预测通过数学物理方法建立确定性模型模拟地下水运动机制，其中特定参数的识别和确定，需要精度较高的数据支撑，且计算量较大，假定条件复杂［2］。近年来随着科技发展和随机论理论的成熟，许多学者将随机性模型应用到地下水埋深预测。随机性模型基于随机理论描述地下水运动过程，主要方法有回归分析法、小波分析法、神经网络模型、时间序列分析模型等，各种模型应用广泛但仍具有一定局限性［3］。自回归滑动平均模型等时间序列分析模型预测精确度较高，但对于非平稳趋势序列和周期性特征处理效果不好［4］；灰色模型所需参数少、容错性小，对历史数据有很强的依赖性，误差偏大；人工神经网络具有较强的容错性和非线性映射能力，但存在运行时间过长，陷入局部最优等问题。近年来，很多专家学者针对不同地区地下水埋深运用了各类模型进行合理预测模拟，徐强等［6］采用多元线性回归模型对北京平原平谷地下水水位动态进行预测；刘雷等［7］采用灰色GM（1，1）理论建立渭北旱塬区地下水埋深预测模型；付强等［8］将人工神经网络进行改进并应用到井灌水稻区进行模拟预测。文献研究表明，专家学者主要运用单一预测模型进行地下水埋深预测研究，因此本文选择五种常见的预测模型，对肇州县地下水埋深进行模拟预测与对比分析，以期了解五种模型在地下水动态预测中性能的优劣，为地下水动态监测预报和地下水资源开采规划提供科学依据。

1 研究方法

1.1 多元线性回归模型

多元线性回归模型是通过建立多元线性回归方程并进行显著性检验来研究因变量和多个自变量之间是否存在线性关系、存在何种数量变化，根据多个自变量的变化来预测模拟因变量值［9］。多元线性回归模型可以有效地综合考虑各个自变量的关系，适用于地下水埋深预测的多因素性。其数学表表达式为：

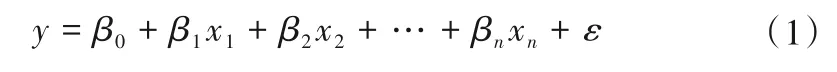
式中：β为样本偏回归系数；ε为随机误差项。

1.2 灰色GM（1，1）模型

灰色GM（1，1）模型是基于灰色系统理论对单变量时间序列数据进行预测的一种预测方法。其基本原理是首先对原始数据进行累加，得到紧邻均值序列和矩阵，运用最小二乘法和求解微分方程对预测模型进行计算，最后将计算值进行累减得到预测结果［10］。具体方法如下：

设有原始非负数据序列为：

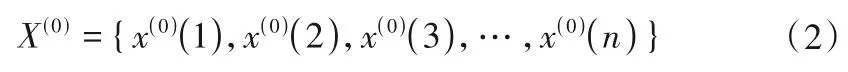
对其进行一次累加处理，得到新的数列：

其中参数a，b可采用最小二乘法确定，即：

进行累减得到灰色GM（1，1）预测值为：

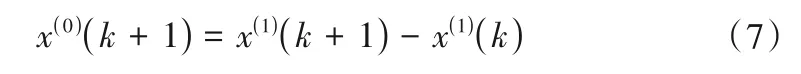
1.3 基于马尔科夫链优化的灰色GM（1，1）模型

马尔科夫链理论基于随机过程理论研究系统从一个空间状态转移到另一个状态的概率进而根据所得到的下一时刻的状态来预测系统未来状态的发展趋势［11］。通过马尔科夫链将灰色GM（1，1）模型预测值与实际值的相对误差进行修正，达到优化灰色GM（1，1）预测值效果［12］。基于马尔科夫链优化步骤如下：

首先对灰色GM（1，1）预测产生的相对误差划分为n个区间状态，建立状态转移概率矩阵：

式中：pij表示从状态Si转移到状态Sj的概率（pij≥0，=1），其中：

式中：Mij表示状态Si出现的次数；Mi表示从状态Si转移到状态Sj的次数。

假设初始状态向量S0，在经过K步转移后的状态向量定义为Sk=S0P(k)。在确定预测状态所处转态序列区间后，就能得到对灰色GM（1，1）优化修正的预测结果［13］，即：

1.4 BP神经网络模型

BP 神经网络模型是一种通过误差逆向传播进行算法训练的多层前馈型人工神经网络模型［14］。网络结构可分为输入层、隐含层和输出层，每层包含若干个神经元，前后层之间通过网络权值相连接，各层神经元之间无连接。选择Sigmoid 型函数作为隐含层的激活传递函数，如：

BP 神经网络学习过程可分为信号正向传播和误差逆向传播两部分，工作信号沿输入层、隐含层、输出层的路线逐层计算传播，当输出层结果与目标输出误差较大时，误差信号反向传播对每个层之间的权值和阈值进行修正，最后回到输入层。两种信号循环反复进行训练，直到将误差控制到期望范围内，学习过程结束。

1.5 基于遗传算法优化的BP神经网络模型

遗传算法按照自然界进化理论模拟染色体遗传、进化、变异的过程形成的全局高效优化搜索算法。遗传算法通过对种群进行选择、交叉和变异操作，将适应度高的个体保留并进行繁衍，产生符合条件的个体即找到最优解［15］。遗传算法具有全局高效搜索能力，可以寻找到BP 神经网络权值阈值最优解，提高模型的鲁棒性，使得最终预测值更加接近实测值。

2 实例应用

2.1 研究区概况

肇州县位于黑龙江省西南方向，地理位置在东经124°48'～125°48'、北纬45°35'～46°16'之间，地形为冲积型平原，地貌较为平坦，占地面积为2 445 km2。肇州县作为农业大县，是全国重要的商品粮基地［16］。肇州县境内无江河，地表水资源匮乏，地下水是肇州县生产生活主要用水来源。受大陆性季风气候影响，肇州县地下水补给主要来源为降雨入渗和侧向径流补给，以人工开采、潜水蒸发和侧向径流方式排泄。

2.2 数据资料

本文选用肇州县1980-2019 年共40 年的年平均地下水埋深资料。在应用多元线性回归模型、BP神经网络模型和基于遗传算法优化的BP 神经网络时，需要明确地下水位埋深变化的主要影响因素［17］。根据研究区地下水动态变化类型并结合相关参考文献，选用降水量、蒸发量、地下水开采量和前期水位共四个因素作为输入变量。五种模型都将1980-2009年地下水位埋深作为训练样本，2010-2019 年地下水位埋深数据作为测试集。

2.3 模型建立及训练

2.3.1 多元线性回归模型

通过SPSS26.0 统计软件建立多元回归线性模型并进行显著性检验，模型建立过程见表1～3。由表1 可知，复变相关系数R为0.893，决定系数R2为0.797，调整后的R2为0.764，表示建立的多元线性回归模型其所选用的自变量可以解释76.4%的地下水埋深的变化［18］。表2中，F=24.524＞F0.05，P=0＜0.01，说明建立的回归模型高度显著具有良好的统计学意义。根据表3 以P＜0.05 为检验水平，蒸发量、降水量和前期水位对于地下水位埋深呈正相关，差异显著；地下水开采量差异不显著［19］。以地水位埋深为因变量，蒸发量、降水量、前期水位为自变量建立多元线性回归预测方程为：

表1 模型拟合汇总Tab.1 Model fitting summary

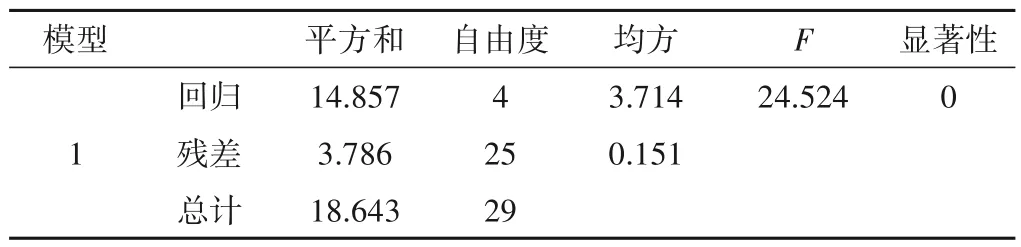
表2 方差分析Tab.2 Analysis of variance

表3 回归系数及显著性检验Tab.3 Regression coefficient and significance test

式中：y为研究区地下水平均埋深；x1为蒸发量；x3为降水量；x4为前期水位。

2.3.2 灰色GM（1，1）模型

根据1980-2019 年肇州县地下水为埋深数据和灰色GM（1，1）模型原理，使用Matlab 进行编程计算，得到各参数值a=-0.010 781 24，u=5.618 878 842，带入到微分方程中，得到模型预测公式为：

2.3.3 基于马尔科夫链优化的灰色GM（1，1）模型

在基于马尔科夫链对灰色GM（1，1）模型进行优化时，需要将灰色GM（1，1）模型训练样本的相对误差进行区间状态划分［22］。训练的相对误差范围为-15.35%～18.64%，分别以-20%、-5%、0、5%、10%、20%为阈值，将其划分为5 个区间状态。确定状态转移矩阵为：

2009 年训练数据处于［-5%～0）状态，确定初始状态向量S0=［0，1，0，0，0］，在经过一步转移后的状态概率向量Sk=S0P(k)=［0，3/5，0，1/5，1/5］。由此可以得到2010 年预测数据相对误差可能处于［-5%～0）状态，即可采用公式对灰色GM（1，1）模型预测结果进行修正。

2.3.4 BP神经网络模型

通过Matlab 编写程序建立BP 神经网络预测模型模拟预测地下水埋深［23］。模型选用三层神经网络结构，输入层神经节点设置为4个，由降水量、蒸发量、地下水开采量和前期水位组成；输出层节点为1 个即研究区地下水位埋深；隐含层节点个数根据经验公式设置为9，确定模型结构为4∶9∶1。隐含层的传递函数选择tansing 函数，输出层传递函数选择purelin 函数，学习算法采用梯度下降法trainlm 函数训练，设置学习速率和训练精度分别是0.01和0.000 01［24］。

2.3.5 基于遗传算法优化的BP神经网络模型

基于遗传算法优化的BP神经网络模型采用和BP神经网络相同的网络结构和参数设置［27］。GA-BP 神经网络模型遗传算法部分采用实数编码的方式，编码长度为55，种群规模为40，进化代数为100，选择操作为轮盘赌法，变异概率0.7，交叉概率为0.1。

2.4 模拟结果对比分析

将5个模型得到的模拟预测值和实际地下水位埋深进行拟合得到预测模型结果对比图，如图1 所示。由图1 可知，多元线性回归模型的预测值小于实际值；灰色GM（1，1）模型的预测值呈线性递增；基于马尔科夫链优化的灰色GM（1，1）模型的预测值可以反映出实际值的波动变化情况；BP神经网络模型预测值较为接近，但个别年份波动误差较大；基于遗传算法优化的BP神经网络预测值更加精准，整体拟合情况最好。具体数值可见表4。

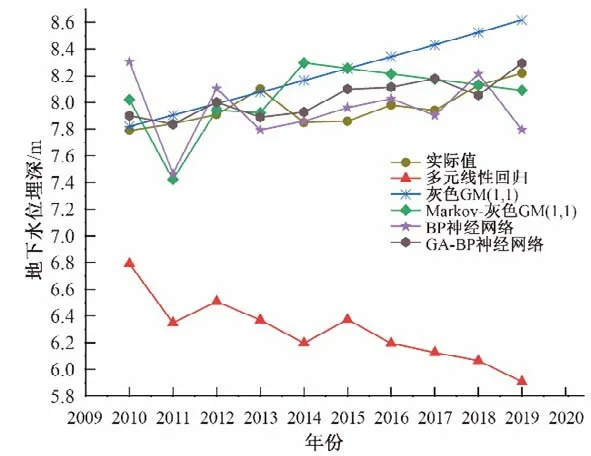
图1 预测模型结果对比图Fig.1 Comparison of prediction model results

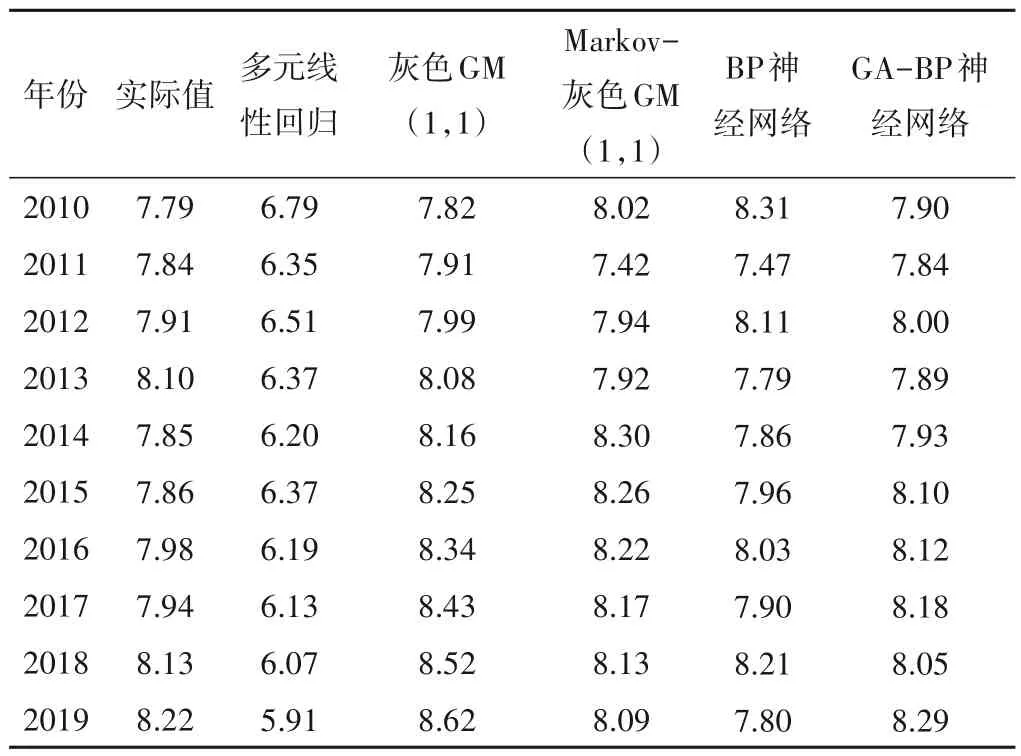
表4 各模型模拟预测值表 mTab.4 Simulation and prediction values of each model

本文采用绝对误差AE、相对误差RE、平均绝对误差MAE、平均绝对百分比误差MAPE、均方误差MSE和均方根误差RMSE作为评价指标对模型预测精度进行评价，计算公式如下：

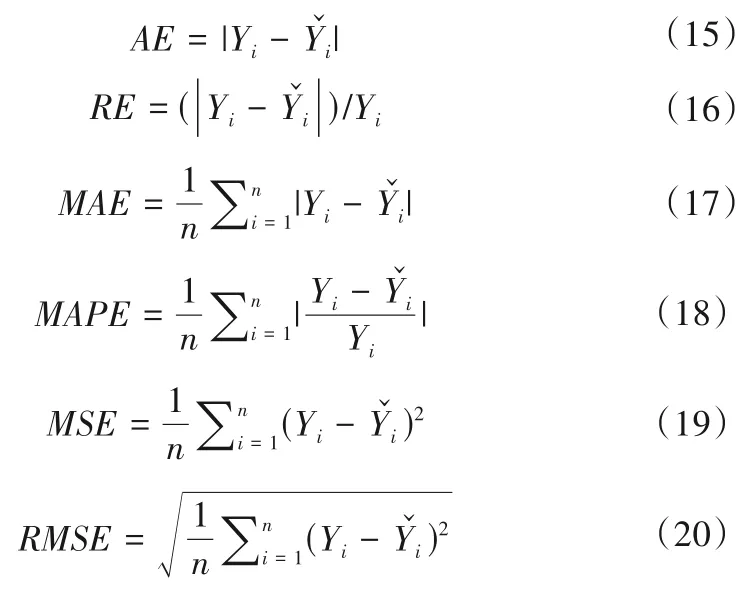
式中：Yi为实际地下水埋深值；为模拟预测值；n为预测个数。

评价指标具体数值可见表4，预测模型的绝对误差和相对误差对比图见图2、3。由表5和图2、3分析可知，GA-BP神经网络模型各项评价指标都比其他四个模型效果好，且预测精度最高，预测结果最稳定，说明GA-BP 神经网络模型可以很好地将遗传算法和神经网络两者优势相结合，既增强全局搜索能力又保持良好的容错性和泛化能力。

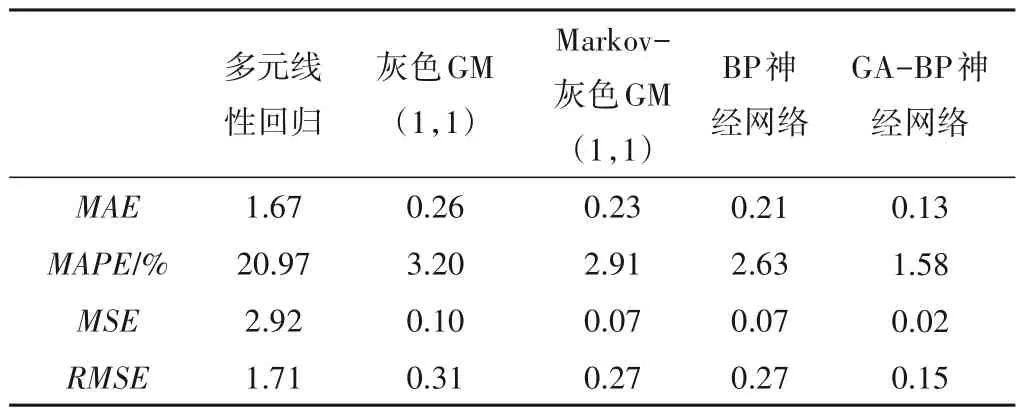
表5 模型性能参数Tab.5 Performance parameters of the model

图2 预测模型绝对误差图Fig.2 Absolute error diagram of prediction model

图3 预测模型相对误差图Fig.3 Relative error diagram of prediction model

5 种预测模型精度和稳定性按由低到高的顺序依次为：多元线性回归＜灰色GM（1，1）＜Markov-灰色GM（1，1）＜BP 神经网络＜GA-BP神经网络。多元线性回归在考虑解决简单的线性问题上效果较好，但影响地下水埋深条件较为复杂，相关因素具有非线性的特点。所以本文在考虑3 个主要因素的影响下，预测结果精度较差。灰色GM（1，1）模型预测结果偏向于数据整体的长期发展趋势［8］，对于均匀增减且无波动的序列预测精度效果较好，所以本次预测结果呈现线性递增现象，误差较大。基于马尔科夫链理论优化的灰色GM（1，1）模型通过转移概率对原始数据序列波动进行修正，相较于灰色GM（1，1）模型提高预测精度，更加可靠。BP神经网络对长序列资料的学习能力较强，整体拟合较好。GA-BP 神经网络的预测值与实际值拟合情况最好相较于其他4种预测模型可以更高效准确地对地下水位埋深进行预测。

由表4 可知BP 神经网络预测的相对误差最大值为6.61%最小值为0.13%，而GA-BP 神经网络预测的相对误差最大值为3.06%最小值为0.04%，表明经过遗传算法优化的BP 神经网络模型可以显著提升预测模拟精度和稳定性；由图4、5 所示，BP神经网络经过五轮训练迭代得到最优解，而GA-BP神经网络仅通过两轮训练，均方根误差就能达到0.024 8，快速收敛且稳定，表明遗传算法优化的BP 神经网络模型训练效率更高。由图6可知，个体适应度随着遗传迭代次数增加不断减小，而个体适应能力不断增强，在经过27次迭代后，个体适应度保持稳定。

图4 BP神经网络训练图Fig.4 BP neural network training diagram

图5 GA-BP神经网络训练图Fig.5 GA-BP neural network training diagram

图6 适应度曲线图Fig.6 Fitness curve

GA-BP 神经网络相较于BP 神经网络的优势体现在：预测模拟结果更加精准、训练效率更加高效和适应能力更强。遗传算法在训练样本阶段通过全局寻优和快速收敛的能力优化BP神经网络权值和阈值，解决了BP 神经网络易陷入局部最优、收敛能力差等问题，同时迭代优选出的适应力强个体，提高预测模型的稳定性。

3 结论

（1）本文选用多元线性回归、灰色GM（1，1）、基于马尔科夫链优化的灰色GM（1，1）、BP 神经网络和基于遗传算法优化的BP神经网络五种预测模型，对肇州县地下水位埋深进行模拟预测，对比分析五种模型的预测结果和适用范围。结果表明：GA-BP 神经网络模型相对误差在0.04%～3.06%之间，绝对误差在0.003～0.24之间，预测精度较高，稳定性好。

（2）本文选择降雨量、蒸发量、地下水开采量和前期水位作为模型的输入层输入应用于肇州县地下水埋深预测，预测结果较为准确，可以为其他地区模型输入参数的选择提供参考。

（3）对于地下水位埋深预测，组合模型两两结合可以优势互补，提高预测结果的准确性和稳定性，达到较小误差科学预测的效果，相较于单一方法具有较高的可行性和实用性。