动态数据校正提升孤岛微电网频率控制性能

黎东阳，张正江，洪智慧，胡 文，章 纯，张振慧

(温州大学 电气数字化设计技术国家地方联合工程实验室，浙江 温州 325035)

0 引言

在实际的控制过程中，需要使用传感器来进行采集信号和传递信号，然而由于传感器自身内部结构、外界环境等原因难以避免的会受到测量噪声的影响，测量噪声有高斯分布形式和非高斯分布形式两种分布类型，这些测量噪声会影响反馈信号的准确性，进而影响到控制器的控制性能，这对于各种控制过程来说显然是不能允许的，为了减小测量噪声的影响，已经有众多的方法被提出和使用。其中各种滤波器已被大量使用在测量信号到达控制器之前，如指数滤波器、移动平均滤波器、指数加权移动平均滤波器等，这些滤波器的当前输出信号是由当前输入信号与之前的输出信号共同决定，尽管这些滤波器具有很好的滤波效果，可以有效地抑制测量噪声的影响，但它们可能会对具有显著动态的过程引入不可接受的时间延迟，故它们大部分适用于稳态过程或者是一些动态较慢的过程[1]，而不适合具有显著动态的过程。

针对上述问题，动态数据校正(DDR，dynamic data reconciliation)可以进行有效解决，动态数据校正技术使用的是实际测量值和模型预测的信息，即使用模型预测信息作为附加信息，通过调和模型的预测值和实际测量值得到对系统反馈信号真实值的估计值，从而很好地减小了测量噪声的影响[2]。因此，动态数据校正技术能够提高系统反馈信号的准确性，从而进一步的提高控制器的控制性能。动态数据校正技术是以最大似然估计和贝叶斯公式为理论依据，相比于指数滤波器和移动平均滤波器、指数加权移动平均滤波器等可以更好的适用于那些具有显著的动态过程中。

近些年来，随着人们对生态环境的保护意识越来远强，同时伴随着传统煤炭、化石、石油等一次能源因为其不可再生性从而面临着枯竭的问题，并且由于这些能源可能会对环境和人体造成各种伤害，比如：化石燃料的燃烧会释放二氧化碳气体，从而造成全球变暖，同时还会产生有毒的二氧化硫气体，这是形成酸雨的罪魁祸首，亦会产生烟尘等从而导致雾霾，同时会对人的呼吸系统造成伤害…从中可以看出一次能源有众多的弊端，为此需要放眼未来，研发洁净和可持续发展的新型能源用来取代化石等传统一次能源。在这种情境下，可再生能源(RES，renewable energy sources)开始走进人们的视野，并越来越受到人们的重视[3]，从而得到广泛的使用。可再生能源的优势是它能够可持续发展，同时分布范围很广，容易获得并且消耗后可以得到及时的恢复和补充，不产生或者极少产生污染物，因此属于清洁能源，目前常用的清洁能源包括：风能、太阳能、核能、地热能、氢能、核能、潮汐能等。伴随着可再生能源的广泛使用，以及相关发电、储能、逆变等技术的发展，微电网这个概念也被更多人所熟知[4]，微电网根据公共连接点(PCC，point of common coupling)的状态有两种工作模式：并网模式和孤岛模式。在并网模式下微电网的频率是由主电网所决定；而在孤岛模式下对于微电网的频率控制是具有一定难度的，由于微电网内发电机组的容量较小，它们的惯性也就较小，这时对于孤岛微电网来说如果其输入的能量是具有一定的波动性，比如输入的能量为太阳能，风能等，或在发电机组发生故障时，那么此时孤岛微电网内所有发电设备所发出的电能之和和负荷端所需要的电能之间将出现能量的不平衡，这将会导致孤岛微电网的频率以及一些其他参数的严重波动。当发电设备所发出的电能多于系统负荷所需要的电能时，孤岛微电网系统的频率将会升高；当发电设备所发出的电能小于系统负荷所需要的电能时，孤岛微电网系统的频率将会降低。因此为了使系统处于稳定并保持良好的性能，通常会在系统中加入储能设备，如飞轮储能系统、电池储能系统[5-7]。这些储能系统会根据电网频率波动的情况实时的进行能量的存储和释放，当发电量大于需求时这些储能装置储存多余的电能，当需求大于发电量时这些储能装置向电网释放电能，从而起到了削峰平谷的作用。然而这些储能设备它们在采集电网频率时需要使用传感器，而使用传感器时就不可避免的会受到测量噪声的影响[8]，而测量噪声的引入将会影响反馈信号的准确性进而影响到孤岛微电网的频率控制性能。故以此为出发点，将DDR滤波技术应用到孤岛微电网频率控制中，同时对以下两种情况下孤岛微电网频率控制的偏差进行了对比：1)当测量噪声为高斯噪声，有无DDR滤波技术时，孤岛微电网频率偏差的方差大小;2)当测量噪声为非高斯噪声，有无DDR滤波技术时，孤岛微电网频率偏差的方差大小。通过有无DDR情况下系统所对应的方差值的大小以及相应输出波形图的对比，验证了动态数据校正滤波技术在孤岛微电网的储能系统反馈控制回路中可有效抑制测量噪声的影响进而显著提升了孤岛微电网频率控制性能，从而为用户带来了更高的用电质量。

1 基于小信号分析的孤岛微电网系统模型

国内外有很多关于混合分布式发电系统和微电网小信号分析的研究和报告[9-11]，图1给出了此次研究中的孤岛微电网示意图，该图中包含各种各样的发电装置，如：太阳能光伏系统(PV, photovoltaic)，风力涡轮发电机(WTG，wind turbine generator)，柴油发电机组(DEG，diesel energy generator)和燃料电池(FC，fuel cells)，同时含有多个不同种类的储能系统，如：飞轮储能系统(FESS，flywheel energy storage system)和电池储能系统(BESS，battery energy storage system)，它们用在孤岛微电网中是为了存储电网中发电装置所产生的多余电能[12-13]，从而保证孤岛微电网中功率的平衡，起到削峰平谷的作用，进而起到稳定孤岛微电网频率的作用。

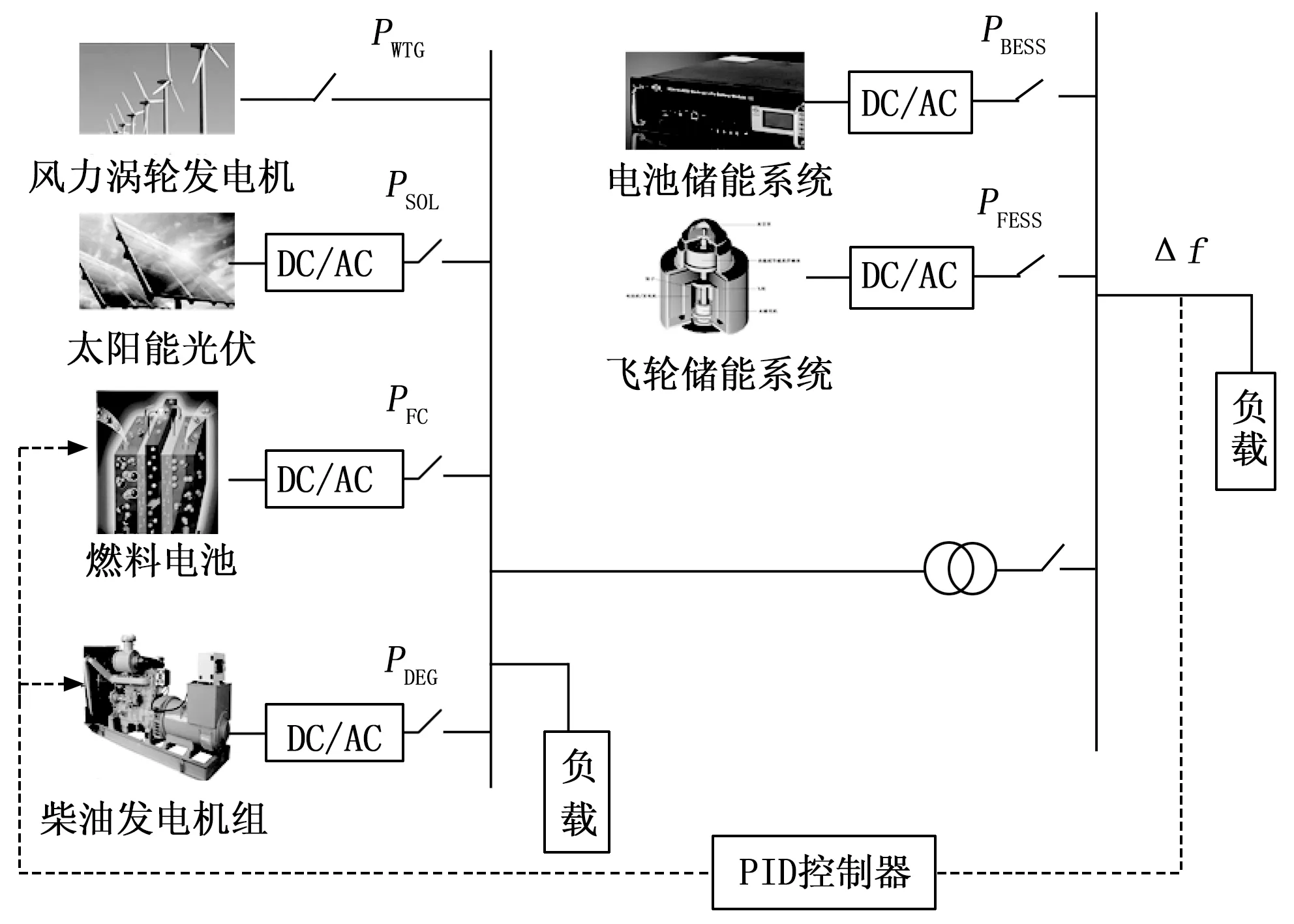
图1 连接有分布式能源的孤岛微电网示意图

图2给出了含有每个部分传递函数的孤岛微电网框图[14]，其中Psol和PW分别是光伏太阳能系统和风力涡轮发电机的输入功率，它们均是一个随机波动的量。PPV、PWT、PDEG、PFC、PBESS和PFESS分别为太阳能光伏系统、风力涡轮发电机、柴油发电机组、燃料电池、电池储能系统、飞轮储能系统的输出功率，Pl是需求侧可变负载所吸收的功率。另外，Pt是光伏太阳能系统和风力涡轮发电机组所产生的功率之和，即：Pt=PPV+PWT，Ps是所有储能系统吸收的功率和所有发电装置产生的功率的总和，即Ps=Pt+PFC+PDEG-PBESS-PFESS，Pe是所产生功率和需求侧所吸收的功率之差：Pe=Pl-Ps，其中Δf表示孤岛微电网的频率偏差。

图2 孤岛微电网方框图

在小信号分析中，PV、WTG、FC、DEG、FESS、BESS可用以下的传递函数进行建模：

(1)

(2)

(3)

(4)

(5)

(6)

式中,TIN、TI/C、TWT、TFC、TIN、TG、TT、TFESS、TBESS均为时间常数，KPV、KFC、KDEG、KWT、KFESS、KBESS均为增益值。各系数的具体数值如表1所示[14]。其中孤岛微电网模型的传递函数由方程(7)所给出，式中D是阻尼常数，H是惯性常数。D和H的值这里分别为0.015 pu/Hz和1/12 pu.sec。对于增益R的值取为3 Hz/pu。其中pu是能量单位，1 pu等于410 kW，sec是秒的单位，Hz是频率的单位。

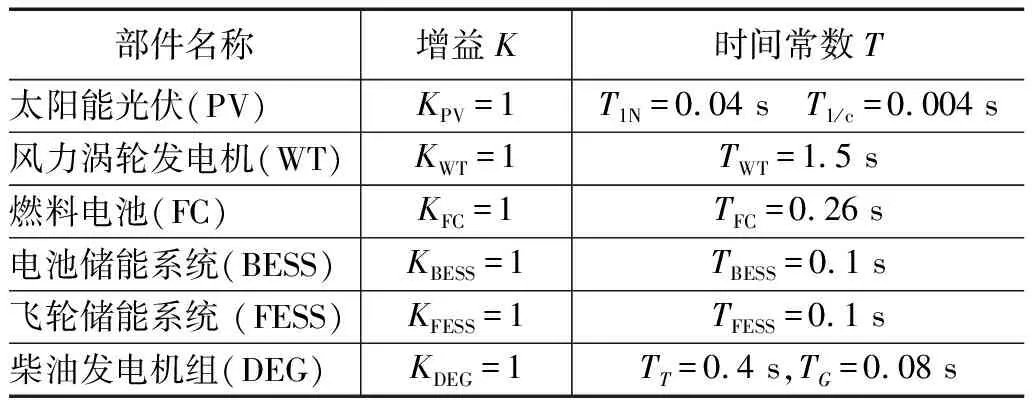
表1 孤岛微电网系统各部件的参数

(7)

对于风力发电、光伏太阳能发电和负荷需求，由于它们本身具有随机的波动性，需要对其进行建模。这些量有各种不一样的建模方法，本篇文章中使用的是公式(8)所示的建模方法，该模型包含了大的确定性漂移和小的随机性功率波动[15]：

(8)

式(8)中，P表示随机的功率，η是一个标准化参数，其是用来标准化产生或需求的电功率χ的常数，以便于和单位(Pu)匹配，φ是一个随机成分，β对功率的平均值有所贡献的参数，G(S)表示的是一个低通滤波器的传递函数，Γ是一个与时间相关的波动信号，其描述了随机功率输出平均值的突然波动。以下分别给出了分布式发电和需求负荷随机模型的具体表达式，其中U(-1,1)表示-1和1之间的一个随机均匀函数，H(t)表达的是一个Heaviside阶跃函数。

对于太阳能发电功率，公式(8)的参数为:

φ～U(-1,1),η=0.1,β=10,

G(s)=1/(104s+1)

(9)

Γ=0.1H(t)-0.04H(t-150)

(10)

对于风力涡轮发电机功率，公式(8)的参数为：

φ～U(-1,1),η=0.8,β=10,

G(s)=1/(104s+1)

(11)

Γ=0.2H(t)+0.1H(t-210)-0.05H(t-270)

(12)

对于需求侧负荷功率，式(8)的参数为：

φ～U(-1,1),η=0.9,β=10,

(13)

对于Γ其表达式如下：

Γ=0.89H(t)+0.06H(t-60)+0.06H(t-90)-

0.2H(t-120)+0.15H(t-180)-0.06H(t-240)

(14)

2 动态数据校正滤波技术

对于含有反馈信号的系统来说，反馈信号的采集需要使用到测量传感器，这一点对于孤岛微电网来说也不例外，由图2可以看出飞轮储能系统和燃料电池储能系统的输入信号均是孤岛微电网的频率偏差信号，该信号就是一个反馈信号，该信号的测量就需要使用到测量传感器，但是，因为测量传感器自身的结构问题以及外界环境等原因，传感器有时并不会工作在理想的状态而是会受到测量噪声的影响，这就会造成反馈的信号是真实的测量信号叠加上测量噪声信号，显然这对于系统的控制是不利的，那么这时就需要使用DDR滤波技术来减少测量噪声对真实信号的影响，从而提高反馈信号的真实性，进而提高控制器的控制性能从而达到减小电网频率波动的目的。以下将分别介绍，在孤岛微电网中，测量噪声分别是高斯信号[2]和非高斯信号[16-17]两种情况下DDR的滤波原理。

2.1 高斯测量噪声下动态数据校正原理

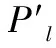
图3 引入DDR后孤岛微电网框图

fm(t)=f(t)+ε(t)

(15)

式中，ε(t)为测量噪声，这里假设该测量噪声是服从高斯分布的噪声即ε(t)～N(0,δ2)，f(t)为反馈信号的真实值，fm(t)为实际的测量值，fddr(t)为DDR的输出信号，即经过滤波后的信号，它是对真实值y(t)经过最大似然估计后所得到的值。根据已知测量的信息fm(t)和其他一些已知的条件，对反馈信号的真实值f(t)来进行估计。首先考虑这样一种情况，即在仅知道fm(t)的条件下对f(t)进行估计，由前面的描述可以知道ε(t)的概率密度函数为：

(16)

再从图3中的关系可以看出：

fm(t)=f(t)+ε(t)

(17)

假设f(t)和ε(t)两者之间是相互独立的，那么基于f(t)下的fm(t)的条件概率密度可以用公式(18)表示：

f(fm(t)|f(t))=f(fm(t)-f(t))=f(ε(t))

(18)

ε(t)～N(0,δ2)，故f(fm(t)|f(t))是一个高斯分布，它的均值是f(t)，方差是ρ2。在给定f(t)条件下时fm(t)的条件概率密度函数和给定fm(t)条件下时f(t)的似然函数等价，则：

(19)

现在的问题转换成了找到f(t)最可能的值(即能够使得L(f(t)|fm(t))最大的值)。根据概率论和数理统计的相关知识可知这样的估计被称为最大似然估计。由上式可以很明显地看出，当f(t)=fm(t)时L(f(t)|fm(t))的值可以取到最大，这表示如果仅知道测量值fm(t)的条件下，对真实值的最佳估计值是测量值，这样的结果显然是难以让人接受的，故需要尝试新的解决办法。

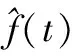
(20)

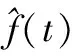
(21)

使用测量信息对上式采用贝叶斯公式可以得到：

p(f(t)|fm(t))

∝L(f(t)|fm(t))p(f(t))

(22)

(23)

(24)

根据最大后验概率估计可以得到，使得式(24)取得最大的f(t)就是对实际f(t)的估计值，也就是fddr(t)，要想让其取最大的值，等价于让式(25)取得最大值：

(25)

根据多元函数极值的相关理论可以知道，想要求得式(25)的最大值可以对式(25)中f(t)求偏导并令其为0，可得：

(26)

对式(26)进行求解，就可以得到对于实际值f(t)的估计，即fddr(t)，可以求得fddr(t)最终值为：

(27)

其中：K=(1+ρ2δ-2)-1。

2.2 非高斯测量噪声下动态数据校正原理

前一节考虑的是测量噪声为高斯测量噪声的情况，许多动态数据校正技术也是基于这一假设所成立的。但是传感器在实际的测量过程中，也会受到由于设备故障，测量设备偏差，校准不良以及人为疏忽大意所造成的误差等原因所产生的粗差信号的影响，对于粗差信号，其值一般是大于正常测量噪声信号，这些粗差信号的加入将会导致测量噪声不再是高斯信号从而变为非高斯信号[18]。其中污染正态分布普遍用于描述这些非高斯测量噪声信号。对于非高斯信号的测量噪声，大部分基于高斯分布测量噪声信号所设计的滤波器(如卡尔曼滤波器、平均滤波器)在滤波时将会表现出较差的性能，因为粗差对系统性能的削弱较为严重，所以也有许多数据校正技术运用到减少粗差的影响中来[19]，然而这些技术大部分都是在稳态的系统中，对于受到非高斯测量噪声影响的动态系统来说，DDR技术很少被设计使用到。故本节主要说明当测量噪声服从污染正态分布时，DDR滤波技术的原理，并推导出此时DDR滤波器的输出表达式[16]。

假设服从污染正态分布的测量噪声可用式(28)表示：

ε(t)=ωε1(t)+(1-ω)ε2(t)

(28)

式(28)中，ε1(t)表示高斯信号，ε2(t)表示粗差信号，同时ε1(t)～N(0,ρ12)，ε2(t)～N(0,ρ22)。(1-ω)表示粗差信号发生的概率。和之前高斯信号下的推理过程同理，可得基于条件fm(t)下f(t)的似然函数表达式如式(29)所示:

L(f(t)|fm(t))=ωp1+(1-ω)p2

(29)

p1=L(f(t)|fm(t))=

(30)

p2=L(f(t)|fm(t))=

(31)

显然此时如果想要估计出参数y(t)的值，也就是使得上述似然函数取得最大值，由函数的特性可知，当f(t)=fm(t)时L(f(t)|fm(t))的值可以取到最大，对真实值的最佳估计值其实只是测量值，故要寻求新的解决办法。

(32)

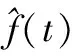
(33)

这时再利用模型的预测值和测量噪声来估计真实知，由贝叶斯公式可知：

(34)

因概率p(f(t))的值恒正，故：

L(f(t)|fm(t))p(fm(t))

(35)

从而可得:

(36)

根据最大似然估计可得，式(36)取得最大值时的f(t)即为估计输出fddr(t)。求解过程如下：

第一步：为取得式(36)最大值，首先对其两边取对数，即：

ln{[ωp1+(1-ω)p2]P3}=

ln{ωp1+(1-ω)p2}+ln(p3)

(37)

其中：

(38)

第二步：对式(37)中f(t)求偏导可得：

(39)

第三步：对式(39)令其值为0可以求得式(36)的最大值，即:

(40)

第四步：求解式(40)可得实际输出的估计值fddr(t)满足以下的条件：

(41)

由此可以得到对真实值的估计值为：

(42)

3 仿真验证与结果分析

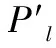
首先考虑当飞轮储能系统和电池储能系统这条反馈回路引入高斯测量噪声的情况，为了降低测量噪声的影响，在孤岛微电网模型中引入DDR滤波器，以下分别考虑了测量噪声方差为1×10-6到5×10-6变化时系统中有DDR滤波器和没有DDR滤波器两种情况，分别对比了在这两种情况下，孤岛微电网频率偏差的输出波形以及频率偏差的方差值。孤岛微电网频率控制器采用PID控制器，其参数经过智能优化后选取为KP=5，KI=3.585 5，KD=1.328 6，对于仿真的时间选取为500秒。

这里选取了测量噪声方差为1×10-6和5×10-6时孤岛微电网频率偏差量的波形图，如图4，图5所示，在表2，表3中展示了有无DDR时孤岛电网频率偏差的方差值大小。

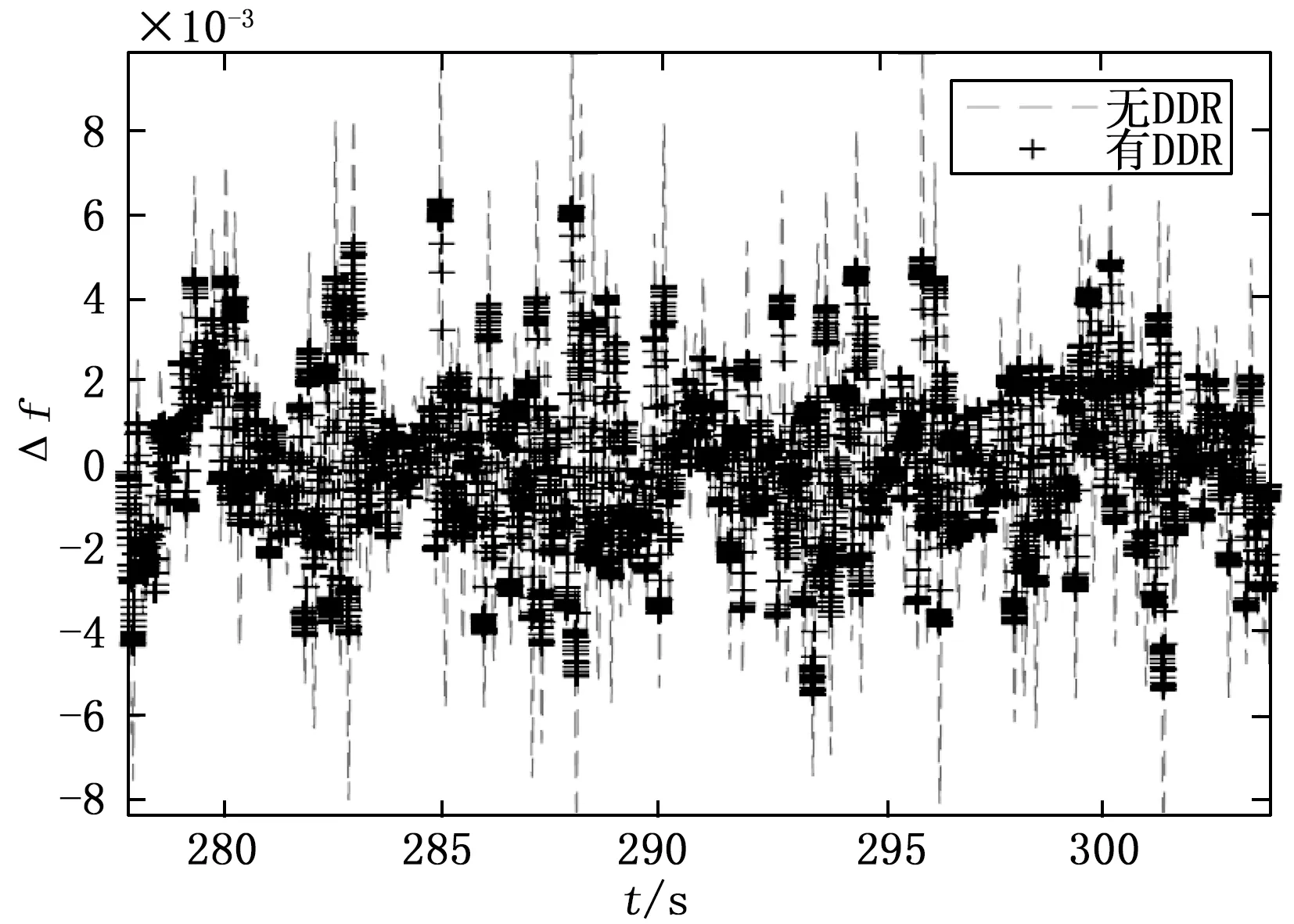
图4 高斯分布测量噪声方差为1×10-6时有无DDR孤岛微电网频率偏差量的比较图

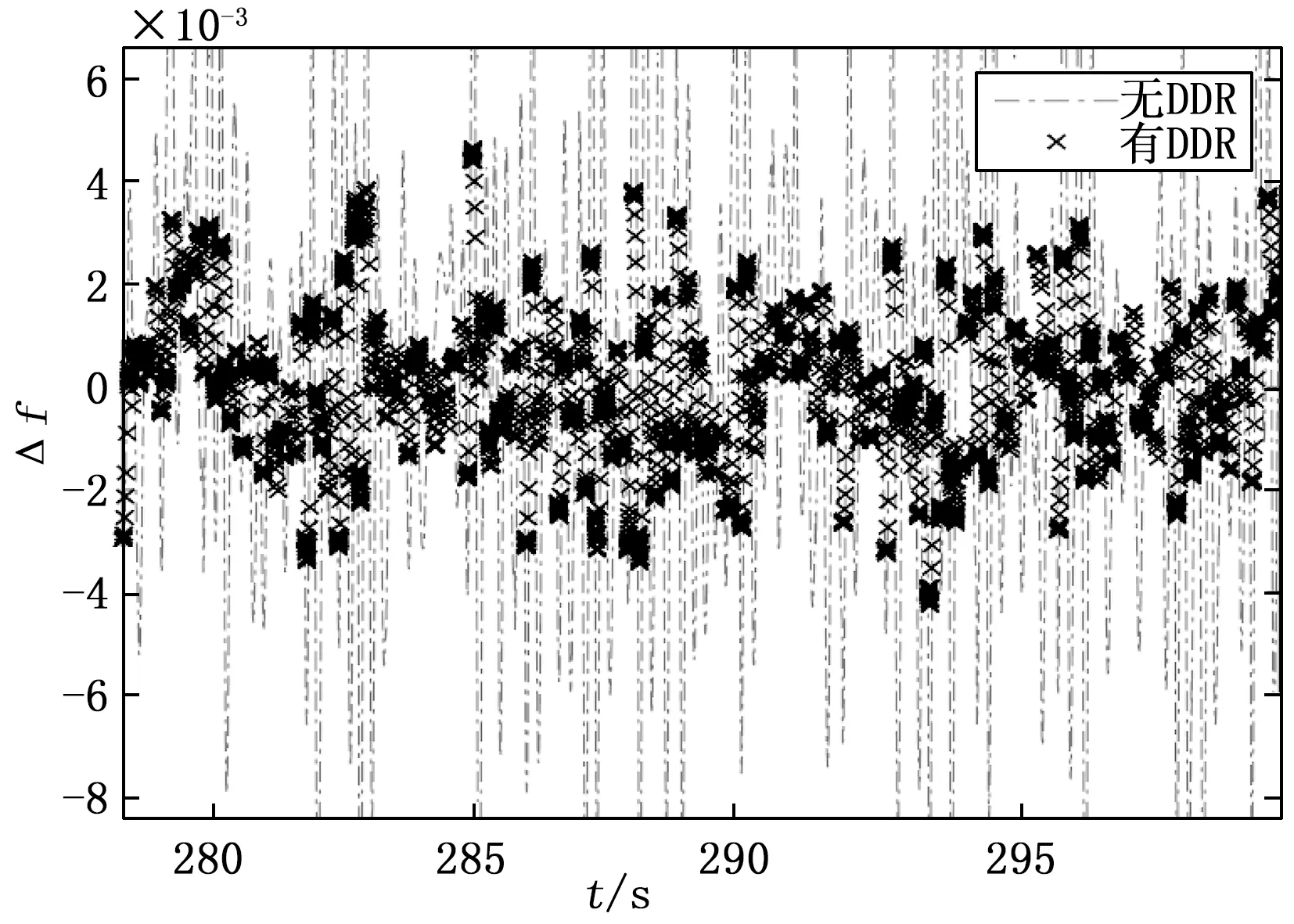
图5 高斯分布测量噪声方差为5×10-6时有无DDR孤岛微电网频率偏差量的比较图

表2，表3是孤岛微电网频率偏差的方差值在不同测量噪声影响下，有无DDR滤波器时的对比。

表3 高斯噪声情况下有DDR时孤岛微电网频率偏差的方差值

从表2，3可以看出，测量噪声的引入会增加控制系统的输出波动性(这里用方差表示，并通过方差值的大小来表示输出波动性的大小)，从图4，图5可以明显看到有无DDR时系统输出波形的对比，在没有DDR滤波器时系统的输出波形具有较大的波动性，而在加入DDR滤波器后系统的输出波形的波动性明显的减少，这也和表2～3中方差值的变化相对应，因此可以知道在加入DDR滤波器后，系统的波动性得以有效的减小，验证了动态数据校正滤波技术在孤岛微电网反馈控制回路中可有效抑制高斯测量噪声的影响从而提升孤岛微电网频率控制性能。

表2 高斯噪声情况下无DDR时孤岛微电网频率偏差的方差值

然而系统中的测量噪声不仅仅只有高斯测量噪声这一种，考虑当传感器在实际的测量过程中，受到由于设备故障，测量设备偏差，校准不良以及人为疏忽大意等原因所产生的粗差信号的影响，这时就如3.2节中所提出的那样，测量噪声便不再是高斯测量噪声，而是一个非高斯测量噪声[20-21]。对此，选取其中最具有代表性的，符合污染正态分布的测量噪声来进行仿真，这里仍然假设在飞轮储能系统和电池储能系统这条反馈回路中有测量噪声的情况，与之前不同的是，此时的测量噪声不再是一个符合高斯分布的测量噪声，而是一个符合污染正态分布的测量噪声。当然，除了本文假设的符合污染正态分布的测量噪声外还有其他很多类型的非高斯分布的测量噪声。对于其他类型的非高斯分布的测量噪声，在已知概率密度函数的情况下，理论上均可使用DDR技术，因为DDR的输出估计值依据的是贝叶斯公式和最大似然估计等知识下的最优估计。

对于污染正态分布，本文考虑对于粗差信号发生的先验概率(1-ω)的值取为1/3，对于ε1(t)，假设是一个方差恒定为5×10-6的高斯信号，而对于粗差信号ε2(t)来说，分别考虑了方差值为1×10-5,1.5×10-5,2×10-5,2.5×10-5,3×10-5这5种情况。针对这五种情况，分别对比了孤岛微电网系统中有无DDR滤波器时的频率偏差的输出波形，并计算了频率偏差的方差值。其中孤岛微电网中PID的参数取值和高斯测量噪声下的PID参数取值一致。这里仿真时间是500 s，首先得到的是有无DDR滤波器时孤岛微电网频率偏差的输出波形对比图，这里选取了粗差信号方差为1×10-5和3×10-5时的波形图对比图，如图6和图7所示，从图6和图7可以看出，当测量噪声为非高斯测量噪声时，系统的输出具有较大波动性，而在加入DDR滤波技术后可以有效减小该系统输出的波动性。

图6 粗差信号较小时有无DDR孤岛微电网频率偏差量的比较图

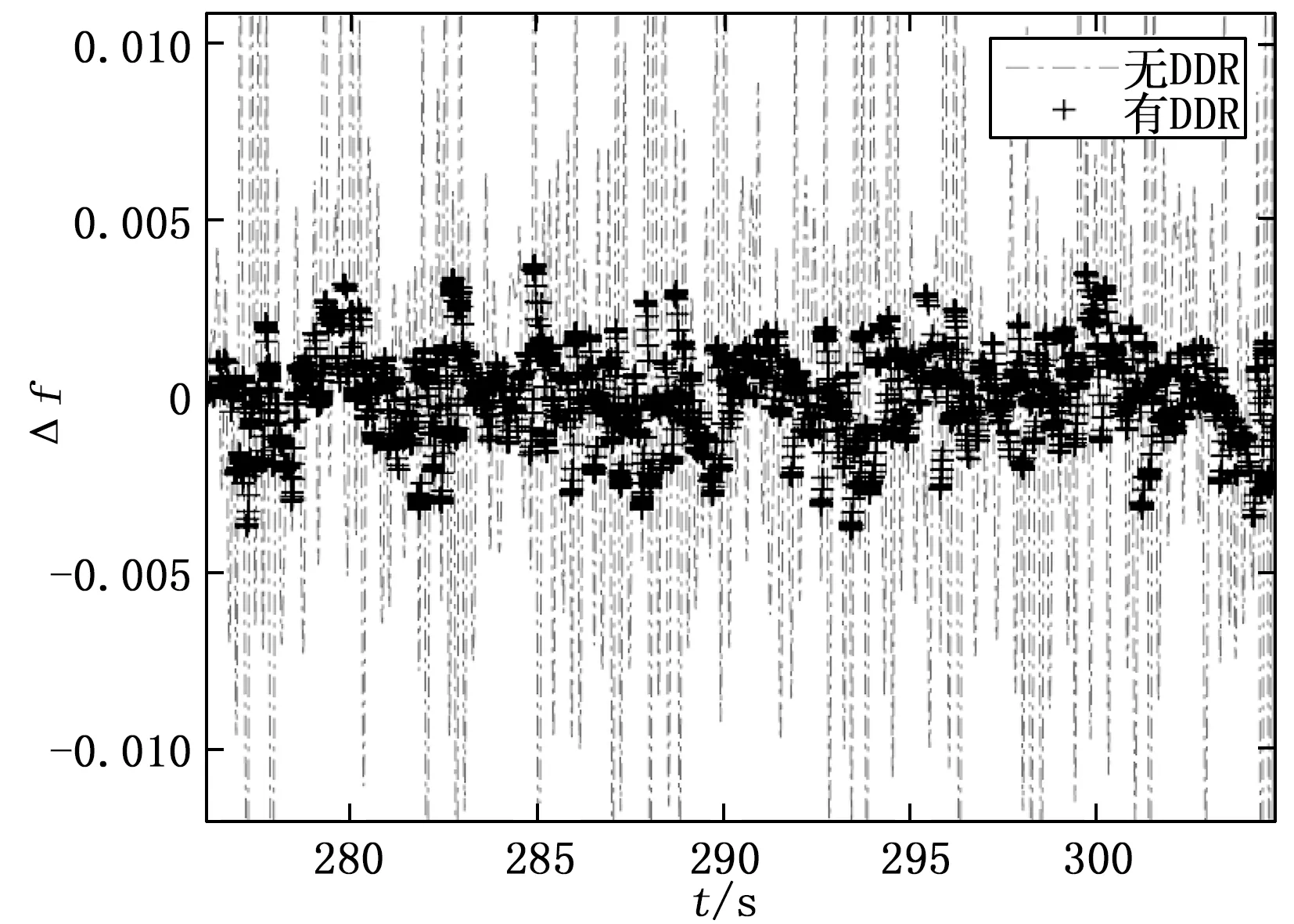
图7 粗差信号较大时有无DDR孤岛微电网频率偏差量的比较图

为了定量的证明DDR滤波技术的应用对孤岛微电网的频率偏差的波动性有很好的抑制作用，以方差为性能指标，分别列出有无DDR时孤岛微电网频率偏差值的方差对比值，结果如表4和表5所示。

表4 非高斯噪声情况下无DDR时孤岛微电网频率偏差的方差值

表5 非高斯噪声情况下有DDR时孤岛微电网频率偏差的方差值

从表4，5中可以看出当加入DDR滤波器后，孤岛微电网频率偏差值的波动性明显的减小，反应在增加DDR后频率的偏差的方差值的减小上。验证了当飞轮储能系统和电池储能系统这条反馈回路中有非高斯测量噪声情况时，动态数据校正滤波技术在微电网反馈控制回路中可有效抑制非高斯测量噪声的影响从而提升微电网频率控制性能。

4 结束语

本文针对孤岛微电网频率控制系统，考虑了在飞轮储能系统和电池储能系统这条反馈回路中的反馈信号受到测量噪声的干扰，从而导致反馈信号的不准确，进而使得孤岛微电网频率波动增大的情况，为了降低测量噪声对孤岛微电网系统的频率偏差Δf的影响，将动态数据校正技术(DDR)运用到孤岛微电网中，并进行了仿真实验。仿真实验过程中，将测量噪声分为了两大类，分别是高斯测量噪声和非高斯测量噪声，这里非高斯测量噪声使用的是具有代表性的污染正态分布。针对这两种情况分别进行了以Δf的方差值为指标的定量分析和微电网输出波形的对比。通过对比了高斯和非高斯两种测量噪声的情况下，有DDR滤波技术和没有DDR滤波技术情况下Δf的方差值，有效地说明了在加入DDR滤波技术后，无论测量噪声是高斯信号还是非高斯信号，动态数据校正滤波技术在孤岛微电网反馈控制回路中均可有效抑制测量噪声的影响，减小孤岛微电网频率偏差波动从而提升孤岛微电网频率控制性能，这对于孤岛微电网的频率控制有着重要的意义。