运用表格分析法优化初中数学应用题教学的研究

贺丽红

（甘肃省天水市武山县渭北初级中学，甘肃 天水）

应用题是通过语言文字来陈述一定事实、反映数学关系并且求解未知量，一直以来都是数学课程中的重点教学部分，也是教学难点。在解答应用题的时候，学生能够加强对所学知识的理解和掌握，同时学生的分析能力、逻辑思维能力都能够得到充分锻炼。在教学实践中，笔者发现通过表格分析的方式能够呈现更为清晰的思路，也能够让学生的解题过程更加顺利，大大提高教学效果。

一、表格分析法概述

数学表征一般可以分成视觉化表征和语言化表征两类。顾名思义，语言化表征就是通过语言文字的表述来说明已知条件和数量关系等，而视觉化表征则是通过具体的图像符号元素来表述相应对象，有突出的形象性与直观性的特点。表格分析通过建立表格，将已知量、未知量显示出来，是视觉化表征的一种形式。通过表格分析法，更容易对题目信息进行分析和提炼，从而寻找到解题的关键点。

在应用表格分析法的时候，应当注意把握以下几点：（1）做好列表准备。在列表解题之前，教师应该做好教育引导，让学生通读题目内容，提取有用信息，用心思考其中涉及哪些数量关系。（2）明确列表原则。使用列表法是为了梳理题目的关系，让解题更加方便，应该依照具体题目决定是否需要通过列表来解答，不要为了列表而列，要尽量精简化。另外，就是在设计表格的时候要注重横向和纵向安排，一般横向表示的是数量关系，而纵向表示的是比较关系。（3）填表顺序。在填制表格的时候应当一边读题一边填写，先填写数字，再填写未知数以及代数式，填好表格之后依据数量间的关系列出方程式。

二、利用表格分析法解决应用题的意义

教师在教学过程当中不应急于让学生去求答案，而要让学生学会如何思考和学习，成为学习的主导者。在传统的数学课堂教学当中，教师总是把重心放在“怎样让学生学会解题”方面，然而却忽视了如何“说思路，找方法，多检验”的过程。从实质上来说，这样的方式并不利于学生解题能力的提升。如果学生长期缺乏思维习惯与思维能力的培养，便容易陷入思维僵化的状态中。“填鸭式”的教学方法和“死读书，读死书”的教学效果都是与当代素质教育目标相背离的。在数学学科教学当中，尤其要倡导“授之以渔”。另外，从学生应用题解题的具体学情来看，造成学生解题失误的原因主要在于学生自身缺乏周密的逻辑思考和分析，而且比较容易马虎大意。从宏观角度来说，数学思维与哲学思想的融合是学好数学的高层次要求。而表格分析法恰恰体现了哲学与数学思维之间的融合，如建立表格反映了关联量之间逆向和顺向、直觉与逻辑、发散与定向等逻辑关系，也映射着实物和实物之间的普遍联系性，反映了或是依从、或是转化、或是对立的哲学内涵；从微观来说，表格分析法是一种合理灵活的解题方式，有助于对命题空间形成清晰认识并且准确把握命题关键。假设学生能够充分而巧妙地应用表格法，就很容易把看似杂糅的数学条理分析透彻。数学应用题当中涉及复杂的量与量之间的关系，常常让学生难以理清头绪，从而对解题抱有抵触心理，对自身能力有质疑，久而久之，学生对数学的兴趣也受到不良影响。而表格能够通过其固有的直观形象性和条理性的优势属性，帮助学生清楚应用题中所蕴含的量。这种方式能够很好地弥补他们分析能力不足的情况，利用表格分析法解题，为学生理清解题思路提供了较好的技巧，能够减轻学生对数学应用题的畏难情绪和抵触心理，树立学习信心。将表格分析法引入初中数学课程教学当中，让教学效果也得到很大提升。

三、利用表格分析法优化数学教学的策略

（一）利用表格分析法解答决策类应用题

关于决策类的应用题是近几年考试中的热点，也比较贴近学生的日常生活。在做决策类应用题的时候，学生能够调动已有的生活经验，知道哪种决策方式是比较经济的选择。然而在决策类应用题中往往包含着大量的信息，容易让学生眼花缭乱，无法抓准重点和理清思路，所以就比较适合利用表格分析法来解题，使用表格法解决决策题目可以让学生在较短的时间内把相关元素对应匹配好，然后对题意形成清晰理解，形成完整的思路框架。

例题，出于经营管理需要，某家大型公司计划购置一批笔记本电脑和投影仪。通过市场调查了解到购置一台笔记本电脑和两台投影仪的费用是3.5万元，购买两台笔记本和一台投影仪的价格为2.5万元。第一问：求一台投影仪、一台笔记本电脑的单价分别是多少元。第二问：据统计，该公司需要购入的笔记本和投影仪的总数为30台。总费用预计不得超过30万元，但是也不可低于28万元。共有几种购置方案可供选择？哪种购置方案最经济？

本题解题步骤如下：①根据相关题干信息，将笔记本电脑的单价设为x万元，将投影仪单价设为y万元。建立表格（如表1）：

表1

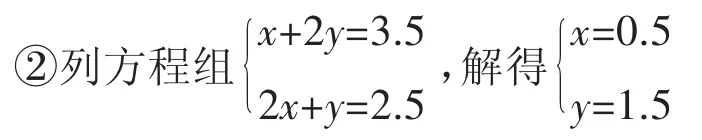
则笔记本电脑单价为0.5万元/台，投影仪单价为1.5万元/台。

在学生通过计算完成第一个问题之后，学生的积极性较高，参与意愿强，教师可以巡视学生情况，接着推进学生解答第二问。师：假设需购进笔记本电脑数量为a台，则购进投影仪的数量为（30-a）。尝试以此列出表格与不等式解答第二问。

①学生结合第一问所得结果以及题干信息，列表格如下（表2）：

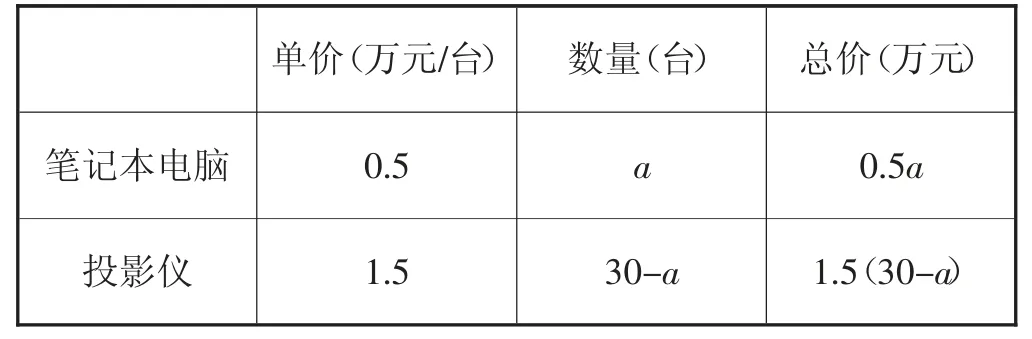
表2

在构建表格和方程组的过程中，学生思维能力得到了锻炼，行动力也得到加强。运用表格分析的方式，避免了由于无效解题而浪费时间。学生通过构建表格，注意力更加集中在分析问题和解决问题上，效率也得到了提高。

（二）利用表格分析法解答销售类应用题

商品销售也是学生日常生活中常常接触到的情境。正常商品买卖应用题计算对初中生来说都很简单。但是在出现打折优惠这类复杂的情况时，一些学生常常容易混淆，难以形成条理，利用表格分析带入不同的价格配置方案，常常能够让问题迎刃而解。

例题：商场销售牙膏与牙刷，牙膏单价为24元/支，牙刷售价为5元/支。为了提高产品销量，现在商场推出了两种促销方案。第一种方案是买一支牙膏赠送一个牙刷，第二种方案是在原价的基础上打九折。有一名顾客买了5支牙膏，牙刷若干（不少于5支）。将客户购买牙刷的数量设为x支。按照商场两种优惠方案来计算付款金额，将方案1付款金额设为A，方案2付款金额设为B。第一问：两种付费方式有何不同，请列式说明。第二问：这名顾客购买多少牙刷的时候，两种方案收费相等？

①根据题干信息，引导学生建立表格进行解题，可得下表（如表3）：

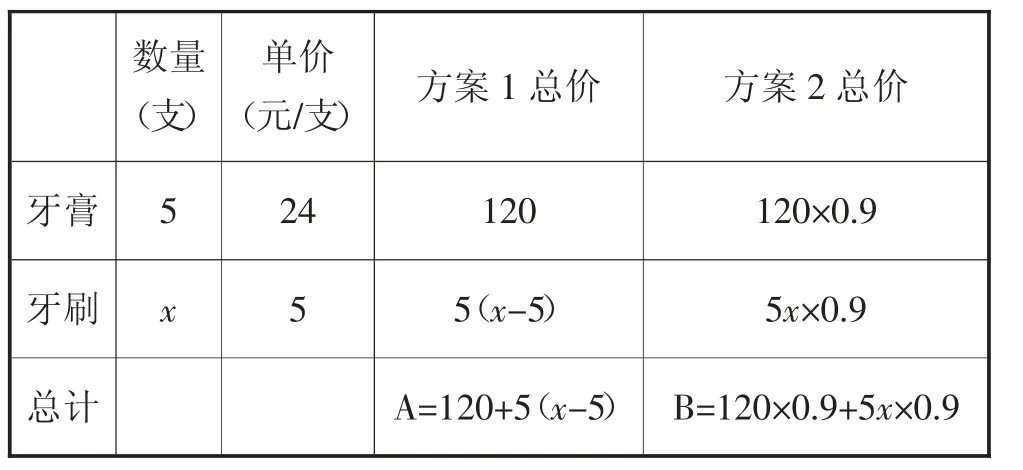
表3

②通过分析易得A=5x+95（x≥5），B=4.5x+108（x≥5）。想要求得顾客购买多少牙刷的时候能够让两种方案价格相等，也就是求解x为多少的时候A=B（即5x+95=4.5x+108）。求得x为26的时候，两种方案付款金额相等。

通过建立表格，两种方案价格的计算方式更加清晰明了，对比也更加鲜明。教师还可以进一步引导学生计算在两种方案总价相同的时候，应付款金额为多少元，以此来巩固练习。

（三）利用表格分析法解决比例增长应用题

比例增长问题也是时常让学生感到“头痛”的一类数学应用题。主要原因在于数量过多容易造成学生对于基数量辨别不清，导致解题方向和最终结果出现错误。教师可以引导学生利用表格分析的方式找出基数量等相应元素，提高解题效率。

例题：某大型超市2021年2月份的销售额为100万元，3月份的销售额下降了20%。针对这种情况，管理部门积极推进整改工作，后期的销售额也得到了相应提升。到了2021年5月份，销售额达到135.2万元。问：4月、5月两个月的平均增长率是多少？

①根据题干信息，将4月、5月两个月的平均增长率设置为x，列出表格（如表4）：

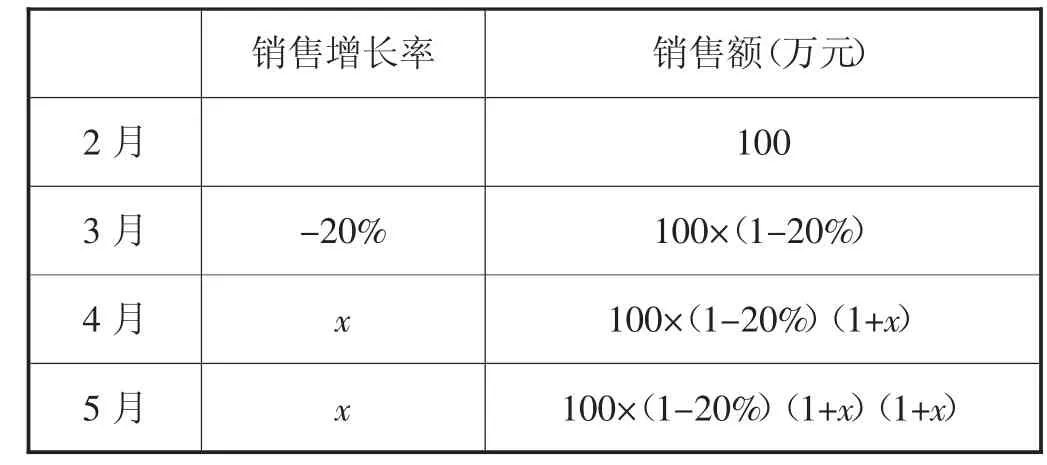
表4

②将题目中已有的数字信息带入其中，形成方程，即5月份的销售额100×（1-20%）（1+x）（1+x）=100×（1-20%）（1+x）2=135.2。学生易求得此方程的解为x1=0.3，x2=-2.3。又因x2=-2.3不合题意，舍去，故而求得x=0.3=30%为本题的解，所以4、5月份两个月的平均增长率为30%。

本题涉及多个时间点、基期量以及增长率信息。学生如果在看题之后直接列式解题的话，常常弄不清楚逻辑，解题不但缺乏效率，而且容易出现计算失误。利用表格分析法来解决比例增长这类问题，能够对不同时间点的基期量、增长率形成一一对应的划分，这样就比较清晰，也不容易出错。

（四）利用表格分析法解决工程类应用题

工程问题学生从小学就有所接触，到了初中时期，依旧是应用题中常见的重点题型。工程类应用题是渗透了函数一一对应的数学思想的题型，也是分数教学知识点的引申与补充。然而在教学实践当中我们不难发现，学生对于工程应用题常感觉无从下手，特别是对于工程总量为“1”的这种设定表示难以理解。针对工程问题这种较为抽象的应用题题型，数学教师不妨引导学生使用表格分析法来解决。

例题：某项手工制造活动，甲师傅单独做的话需要4个小时能够完成，乙师傅单独做的话，需要8个小时才能够完成。如果甲师傅先单独操作半小时，然后甲、乙两位师傅共同合作的话，还需要多少小时能够完成这项工作？

本题的难点主要在于两者并非同时开展工作，而是先后进行，又有共同合作。而且对于具体工程量没有明确数值。所以学生就觉得过于困难。教师可以引导学生建立表格，把工程量问题划分清楚，具体如下：

①设甲、乙两位师傅合作的话还需要x小时能完成。将工程总量视为整体1，那么甲师傅工作效率为，乙师傅工作效率为。甲师傅的工作时间为x）小时，乙为x小时。学生将整理好的信息代入表格当中（如表5）

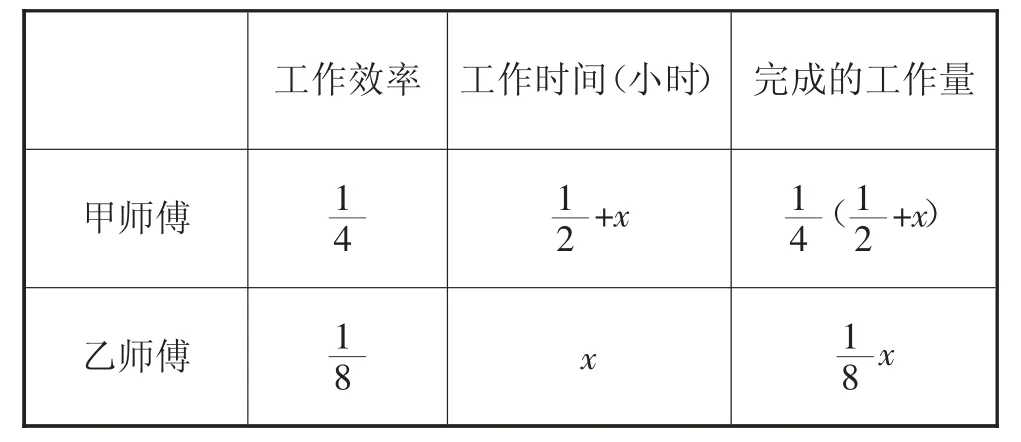
表5

②通过构建出来的表格，题目中的数量关系清晰呈现在眼前。下一步就是引导学生构建方程，即构建方程之后学生就能够容易求得答案。由此可见表格分析法对于梳理应用题的益处。

总而言之，应用题是学生学习数学知识的一个重点，同时解答应用题也是测试和培养学生知识运用能力和思维灵活性的重要方式。将表格分析法引入初中数学应用题教学课堂是一种成效显著的方式，表格分析法对学生梳理题目逻辑、分析题干内容提供了良好的引导，值得在教学中进行使用和推广。广大教育者还应注重钻研，寻求灵活新颖、科学好用的教学方法，帮助学生提高数学能力。