关于形式三角矩阵环的一点注记

王修建，岳 芹，李 露

(皖西学院 金融与数学学院，安徽 六安，237012)

全文考虑的环均为有单位元的结合环，所有的模均为单式模。假设A,B是环，M是左B-右A-双模，设集合

定义T上加法为普通矩阵的加法，乘法为

则T是一个环，称为一个形式三角矩阵环。

形式三角矩阵环作为一般矩阵环的推广是十分重要的，它可以用来构造环论与模论中的反例。文[1]中研究了形式三角矩阵环的一些环论性质，文[2]中讨论了形式三角矩阵的模，文[3]中进一步地刻画了形式三角矩阵环的特殊性质。受国内外研究形式三角矩阵环的内容启发，本文刻画了几种特殊环的形式三角矩阵性质，讨论了形式三角矩阵环的P-内射环，探讨了广义稳定环以及形式三角矩阵环上幂零性。

1 P-内射环

环R称为左(右)P-内射环，如果对每个同态f:Ra(aR)→R，存在c∈R使得对任意x∈I有f(x)=cx(xc),其中a∈R[4](P75)。

引理1.1[4](P75)对任意环R，下述等价：

(1)R是一个左P-内射环；

(2) 对任意a∈R，rl(a)=aR；

(3) 对任意a,b∈R，r(Ra∩l(b))=r(a)+bR.

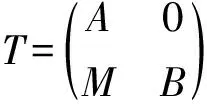
(1)A和B都是左P-内射环；

(2) 对任意的a,a′∈A,b,b′∈B,m,m′∈M，有

rM(Bb∩lB(b′)∩lB(m′))=rM(b)+m′A+b′M.

证明：对任意的a,a′∈A,b,b′∈B,m,m′∈M，

由

可得

以及

于是有

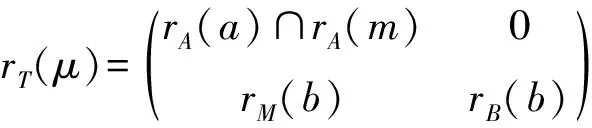
因为T是左P-内射环，由引理1.1知rT(Tμ∩lT(ω))=rT(μ)+ωT，因此我们有

在(1)式中取M=0，可得rA(Aa∩lA(a′))=rA(a)+a′A，在(2)式中取m′=0，可得rB(Bb∩lB(b′))=rB(b)+b′B，根据引理1.1，由a,a′∈A,b,b′∈B的任意性知A和B都是左P-内射环。同时，对任意的a,a′∈A,b,b′∈B,m,m′∈M，可得

rM(Bb∩lB(b′)∩lB(m′))=rM(b)+m′A+b′M。

而一个环R是右P-内射环当且仅当对任意a,b∈R，有l(bR∩r(a))=l(b)+Ra[5]。结合定理1.1以及文[3]不难证明下述结论。

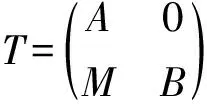
(1)A和B都是右P-内射环；

(2) 对任意的a,a′∈A,b,b′∈B,m,m′∈M，可得

lM(aA∩rA(a′)∩rA(m′))=lM(a)+Ma′+Bm′.

2 幂零性和广义稳定环

引理2.1[6]环R是一个弱-Abel环当且仅当对任意的a,e2=e∈R，若ae=0，则一定有ea∈J(R)。

引理2.2[1]下述条件成立

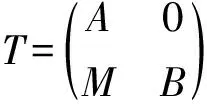
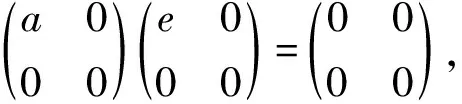
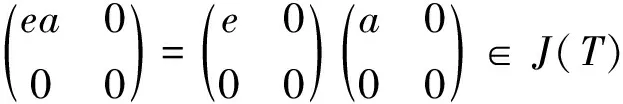
通过引理2.1知ea∈J(A)，所以由a,e的任意性可知A是弱-Abel环。

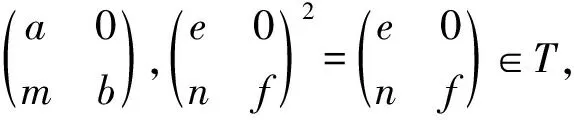
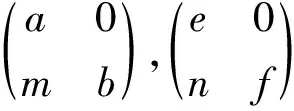
环R称为广义稳定环[7]，如果aR+bR=R，a,b∈R可推出有y∈R使得a+by∈K(R)，其中K(R)={x∈R|存在s,t使得sxt=1}。

定理2.2 若形式三角矩阵环T是广义稳定环，则A和B都是广义稳定环；反过来，若A和B都是广义稳定环且m1+m2a=0(*)对任意的a∈A,m1,m2∈M成立，则T是广义稳定环。

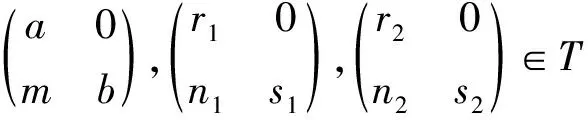
于是r1(a1+a2a)r2=1，因此A是广义稳定环。

类似于上述关于A是广义稳定环的讨论过程，即证B也是广义稳定环。

故由定义条件知T为广义稳定环。

称一个环R是N-诣零环[8]，如果对任意的a∈R都有与a相关的正整数n和k使得(na)k=0。

结合文[8]，易得

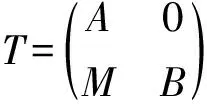
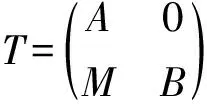
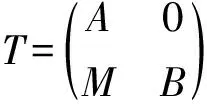
3 结语

利用形式三角矩阵环的性质，刻画了形式三角矩阵环的P-内射性和形式三角矩阵环的广义稳定性，进一步丰富了环论的研究，同时也是对形式三角矩阵环内容的有益补充。