钢-UHPC组合梁受弯性能非线性分析

2022-10-26王洪国龙关旭徐传昶朱经纬宋秀豪

山东建筑大学学报 2022年5期

王洪国龙关旭徐传昶朱经纬宋秀豪

(1.山东高速建设管理集团有限公司，山东济南 250099；2.山东高速集团有限公司创新研究院，山东济南250000；3.山东高速工程检测有限公司，山东济南 250002；4.山东建筑大学交通工程学院，山东济南 250101)

0 引言

超高性能钢纤维混凝土(Ultra-High Performance Concrete，UHPC)为由高度致密基体和细钢纤维组成的新型水泥基复合材料，具有低渗透性和拉压荷载作用下的高强度和高延性特性[1-3]。采用UHPC作为翼板的钢-UHPC组合梁具有自重轻、承载力高、跨越能力大等性能优势[4-5]。钢-UHPC组合梁中UHPC材料的高抗拉强度、高耐久性为解决连续组合梁负弯矩区桥面板受拉易开裂的难题提供了有效途径[6]，优异的力学性能和显著的综合效应使该组合梁成为极具推广价值的新型高性能组合结构[7-8]。

UHPC复合结构是当前土木工程领域的研究热点，但钢-UHPC组合梁作为一种新型结构，目前仅有少量文献对其力学性能开展研究。张彦玲等[9]数值分析了钢-RPC组合梁抗弯性能，建立了塑性破坏模式下钢-RPC组合梁正截面抗弯承载力计算公式。邵旭东等[10]开展的钢-RPC组合梁推出试验表明，RPC由于超高强度而基本不发生破坏，栓钉直径是决定短栓钉抗剪承载力的关键因素。JORGEN等[11]针对钢-UHPC华夫板轻型组合梁进行了足尺条带模型试验，试验结果较好地验证了设计方案及配筋方式的合理性。刘君平等[12]开展了钢-UHPC组合梁与钢-常规混凝土组合梁的抗弯性能对比性试验，获得了两类组合梁的挠度、应变及承载性能对比规律，研究表明了在极限抗弯承载力近似的情况下，钢-UHPC组合梁桥面板的厚度可大幅降低。

受钢与混凝土材料弹塑性及相互作用关系的影响，钢-UHPC组合梁在荷载作用下表现出显著的非线性特性，准确模拟材料特征与界面关系是钢-UHPC组合梁有限元分析的关键。文章采用ABAQUS程序对钢-UHPC组合梁进行非线性有限元分析，基于推导的UHPC损伤塑性本构建立钢-UHPC组合梁应用实例损伤力学数值模型，通过对比试验数据验证数值模型的有效性，进一步对钢-UHPC组合梁受弯性能进行变参数扩展分析。

1 UHPC损伤塑性本构

1.1 UHPC单轴本构

对于UHPC单轴受拉本构，采用上升段、下降段均为斜直线的本构关系模拟。曲线上升段采用文献[13]提出的UHPC单轴拉伸模型，下降段采用线性拉伸软化模型。UHPC单轴受拉应力σt由式(1)表示为

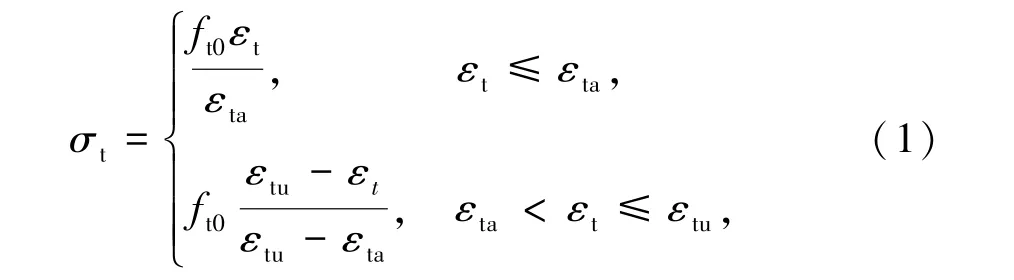
式中εt、εta、εtu分别为UHPC单轴受拉应变、峰值应变及极限应变；ft0为UHPC单轴抗拉强度，MPa。

对于UHPC单轴受压本构，采用上升段、下降段均为抛物线的本构关系模拟。曲线上升段采用文献[14]提出的UHPC单调加载受压模型，下降段采用文献[11]提出的理论模型。UHPC单轴受压应力σc由式(2)表示为

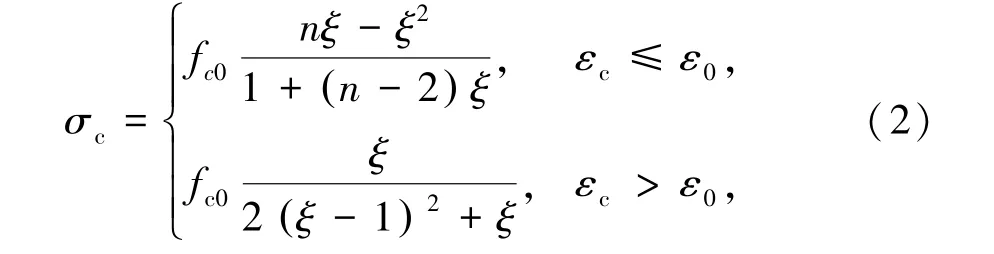
式中ξ为UHPC受压应变比，ξ＝εc/ε0，其中εc、ε0分别为UHPC单轴受压应变和单轴受压峰值应变，ε0取值为0.0035；fc0为UHPC单轴抗压强度，MPa；n＝E0/E1，其中E0、E1分别为初始弹性模量和峰值点割线模量，E1＝fc0/ε0GPa。

1.2 UHPC损伤因子推导

依据Sidoroff能量等价原理，有效应力可由式(3)表示为

式中σ为材料单轴受力应力，MPa；E为自然常数。

依据材料损伤应力张量关系，有效应力可由式(4)表示为

式中d为材料损伤因子。

根据式(3)和(4)，材料损伤因子d可由式(5)表示为

式中ε为材料单轴受力应变。

将式(2)代入式(5)，可推导出UHPC单轴受压损伤因子dc由式(6)表示为

当UHPC单轴受拉本构采用斜直线时，由于无法按材料损伤时的刚度逐渐衰减原理表征损伤因子，故UHPC受拉损伤因子dt不能采用上述公式推导而需重新定义。dt可采用线性损伤假定，在UHPC极限拉伸应变时对应的取值为0.9。

2 有限元模型建立

2.1 几何模型

为验证依据UHPC损伤塑性本构参数建立的钢-UHPC组合梁有限元模型的可靠性，取文献[12]中钢-UHPC组合梁进行非线性计算分析。计算的试验梁模型的跨径为5000 mm，总高为440 mm。钢梁采用HN 350×175×7×11型钢，其屈服强度为253 MPa、弹性模量为200 GPa。UHPC翼板尺寸为300 mm×90 mm，抗折强度、抗压强度分别为17.4、133.3 MPa，而弹性模量为38.8 GPa。栓钉剪力件直径为16 mm，纵、横向间距分别为110、85 mm。试验梁采用跨中1000 mm间距双点加载，其立面构造及加载如图1所示，横截面及配筋如图2所示。

图1 钢-UHPC组合梁立面构造及加载示意图/mm

图2 钢-UHPC组合梁横截面构造及配筋图/mm

2.2 材料模型

UHPC材料本构采用ABAQUS中CDP模型，结合UHPC实测材性，并基于已建立的UHPC损伤塑性本构模型，计算得到UHPC受拉损伤因子dt与受压损伤因子dc。钢材采用双线性等向强化模型，其泊松比为0.3、硬化斜率为1/200E0。

2.3 界面模型

对于钢梁与UHPC翼板之间的界面连接栓钉，其刚度关系采用文献[11]提出的3向荷载(Q)-滑移(δ)模型，由式(7)表示为

式中δx、δy、δz分别为栓钉沿x、y、z方向位移，mm；Qx、Qy、Qz分别为栓钉沿x、y、z方向位移所对应荷载，kN；Lst为栓钉长度，mm；Est为弹性模量，MPa；Ast为横截面面积，mm2；Qu为栓钉的极限抗剪承载力，其计算公式由式(8)表示为

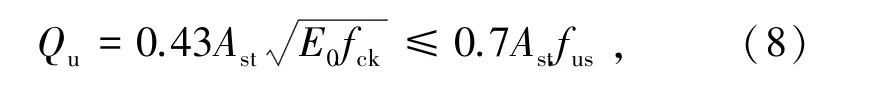
式中fck为混凝土圆柱体标准抗压强度，MPa；fus为栓钉极限抗拉强度，MPa。

2.4 有限元模型建立

UHPC、钢材分别采用C3D8R和S4R单元模拟。界面连接栓钉采用纵向、横向及竖向3个正交力学性能的弹簧单元SPRING2模拟。依据计算实例构造尺寸建立几何模型，并应用结构化网格划分技术，控制UHPC翼板网格尺寸为50 mm、钢梁网格尺寸为25 mm，从而进行几何模型网格划分[15]。有限元计算时考虑材料、几何双重非线性及非线性弹簧单元特性进行求解分析，建立的钢-UHPC组合梁有限元模型如图3所示。

图3 钢-UHPC组合梁有限元模型图

3 模型破坏形态及结果验证

钢-UHPC组合梁数值模型中梁UHPC翼板损伤演化分布如图4所示。其中，F、Fuc分别为数值模型梁施加荷载与极限荷载。模型梁在荷载为0.53Fuc时达到钢梁下翼缘初始屈服状态，在荷载为0.78Fuc时达到钢梁下翼缘应变强化状态，在荷载为0.85Fuc时在跨中UHPC翼板底面两侧悬臂位置发生初始受拉损伤，而荷载为0.87Fuc时发生初始受压损伤。承载能力极限状态时，模型梁跨中截面钢梁处于完全屈服状态，UHPC翼板底面受拉损伤扩展到加载点内全部范围。模型梁UHPC翼板损伤演化发展过程与试验梁UHPC翼板出现裂缝的荷载、分布规律一致。

图4 UHPC翼板损伤演化图

数值计算与试验全过程荷载-跨中挠度、荷载-应变曲线对比分别如图5、6所示。由图5可知，数值模型与试验梁变形响应趋势较为一致。但数值计算除可获得钢-UHPC组合梁的弹性、弹塑性及破坏3个基本受力阶段外，还可获得随荷载降低而变形逐渐增大的下降段，该下降段的变化趋势可用于进一步评估组合梁的延性性能。分析数值计算较试验梁体现更好延性性能的原因主要是:在接近承载能力极限状态时，常规加载系统控制调节落后于承载力变化而引起其储存的弹性能瞬间释放，致使试验梁翼板达到压溃应变时即达到承载力极限，而无法继续展现承载力下降段。而模型梁在UHPC翼板压溃后，可继续进入UHPC本构的下降段，试验梁的延性能得以充分发挥。由图6(a)的荷载-UHPC翼板顶面纵向应变曲线和图6(b)的荷载-钢梁下翼缘底面纵向应变曲线对比可知，数值模型与试验梁应变响应趋势较为一致，但数值模型较试验梁的弹塑性抗弯刚度略大，这主要是由于数值模型为理想化模型，而实际结构存在一定的初始缺陷所导致。

图5 数值计算与试验全过程荷载-跨中挠度曲线对比图

图6 数值计算与试验全过程荷载-应变曲线对比图

由上述分析可知，数值模型与试验梁UHPC翼板损伤发展及全过程曲线的响应规律较为吻合，表明采用文章方法建立的钢-UHPC组合梁的数值模型能够较好地预测钢-UHPC组合梁非线性受弯破坏行为。

4 不同参数对受弯性能影响分析

在已验证数值模型应用参数的基础上，进一步分析构造尺寸、材料强度参数变化对钢-UHPC组合梁受弯性能影响规律。选取UHPC抗压强度fu、钢材屈服强度fy共2个材料强度参数及代表截面各部分组成构造的UHPC翼板厚度Tu、下翼缘宽度Df及腹板厚度Tw共3个截面构造参数为变量，分析参数变化对钢-UHPC组合梁的抗弯刚度、极限承载力Fuc、屈强比η、位移延性系数k等主要力学性能的影响。共建立25个钢-UHPC组合梁有限元计算模型，模型基本参数及计算获得的极限承载力见表1。有限元模型计算的荷载-跨中挠度曲线随各参数变化规律如图7所示。

图7 有限元模型计算荷载-跨中挠度曲线图

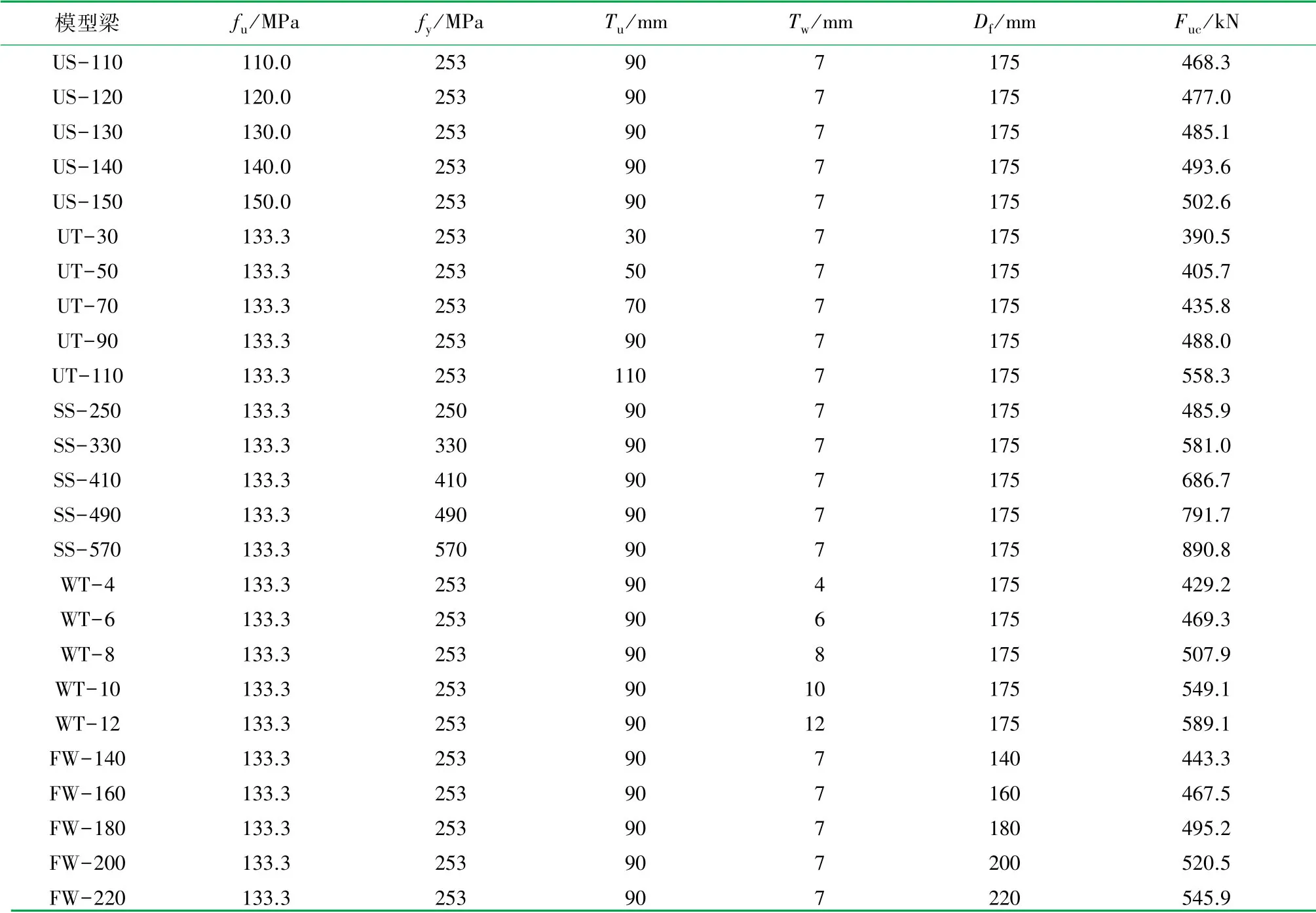
表1 模型梁参数及极限承载力表

图7(a)中变化参数为UHPC屈服强度。随UHPC抗压强度fu的增大，组合梁的弹性抗弯刚度、屈服承载力不变；当UHPC抗压强度由110 MPa均匀增大至150 MPa时，组合梁的极限承载力Fuc均匀提高至7.3%，屈强比η由0.58均匀下降至0.55，而位移延性系数k由22.9均匀增大至34.9，组合梁的延性性能提高。

图7(b)中变化参数为UHPC翼板厚度Tu。当UHPC翼板厚度由30 mm分别增大到50、70、90、110 mm时，组合梁的弹性抗弯刚度均匀提高；极限承载力Fuc分别提高3.9%、11.6%、25%、43%，Fuc提高幅度逐渐增大；屈强比η由UHPC翼板厚度为30、50 mm时的0.66分别降低至0.56、0.55、0.53，η在UHPC翼板厚度由50 mm增大至70 mm时显著降低。当UHPC翼板厚度由30 mm增大至50、70 mm时，位移延性系数k由11.71均匀增大至19.47；此后当UHPC翼板厚度增大至90、110 mm时，k由19.47均匀减小至11.5。因此随UHPC翼板厚度的增大，k呈现先增大后减小的变化规律。

图7(c)中变化参数为钢材屈服强度fy。随钢材屈服强度的增大，组合梁的弹性抗弯刚度不变，屈服承载力增大。当钢材屈服强度由250 MPa均匀增大至570 MPa时，组合梁的极限承载力Fuc均匀提高至83.3%，屈强比η由0.61均匀增大至0.76。位移延性系数k由钢材屈服强度为250 MPa时的26.4分别降低至13.1、10.4、6.1、4.8，而钢材屈服强度由250 MPa增加至330 MPa时，k显著减小，此后随着钢材屈服强度的增大，k减小幅度逐渐降低。

图7(d)中变化参数为腹板厚度Tw。随腹板厚度的增大，组合梁弹性抗弯刚度、屈服承载力均匀增大。当腹板厚度由4 mm均匀增大至12 mm时，钢梁用钢量均匀增加至50.8%，极限承载力Fuc分别提高9.3%、18.3%、27.9%、37.2%，屈强比η由腹板厚度分别为4、6 mm时的0.58、0.61增加到其他腹板厚度时基本恒定值0.64。位移延性系数k由腹板厚度为4 mm时的37分别减小至27.8、20.5、17.8、15.3，k减小幅度逐渐降低。

图7(e)中变化参数为钢梁翼缘宽度Df。随翼缘宽度的增大，组合梁的弹性抗弯刚度、屈服承载力均匀增大。当翼缘宽度由140 mm均匀增大至220 mm时，钢梁用钢量均匀增大至40%，极限承载力Fuc均匀提高至23.1%，屈强比η由翼缘宽度为140 mm时的0.61增加至其他宽度时的基本恒定值0.66。位移延性系数k由翼缘宽度为140 mm时的25.9分别变化至26.6、19.2、18、16，k呈现先增大后减小的趋势。

综合上述参数的分析可知，钢-UHPC组合梁极限承载力Fuc随钢梁翼缘宽度、腹板厚度、UHPC翼板厚度的增大有一定提高，随钢材屈服强度的增大提高最为显著，而随UHPC强度等级的增大提高较小。屈强比η随钢材屈服强度的增大提高最为显著，随腹板厚度、翼缘宽度的增大而提高较小，随UHPC强度等级、UHPC翼板厚度的增大而减小。位移延性系数k总体上随UHPC强度等级的增大而显著提高，随钢材屈服强度、腹板厚度、钢梁翼缘宽度的增大而显著降低，且随UHPC翼板厚度的增大，呈现先增大后减小的趋势。