基于混合神经网络的时序不平衡分类研究
2022-10-26毛玉明杨留方曹伟嘉谢宗效
毛玉明,杨留方,曹伟嘉,谢宗效
(云南民族大学 电气信息工程学院,云南 昆明 650500)
对于传统分类任务,属性的值是独立于属性的发生顺序的,而对于时间序列,正是属性的发生顺序使得样本具有独特性,其难点就是怎样挖掘出数据样本前后所隐藏的特殊逻辑关系,这些逻辑关系包括数据点的先后,局部子序列的特征,数据维度高以及噪声节点等.目前,针对时间序列分类有以下几种分类方式.①采用计量距离的全序列的分类方法,如DTW[1]、WDTW[2]、TWE[3](time warp edit)等算法,这类方法是计算整个时间序列间的相似度来判断所属类别的.②基于区间的分类方法,其中具有代表的算法是TSF[4](time series forest)和TSBF[5](time series bag of forest),其都采用了随机森林的思想,并通过随机采样来减少选取的复杂度.③采用shapelets分类方法,代表算法有将shapelets发现过程融入二叉决策树的Shapelets发现算法[6-8](shapelet discovery algorithms),将shapelets的提取与分类的构建相分离的Shapelets变换算法[9](shapelet transform algorithms).④深度学习的方法,近几年深度学习、机器学习的快速发展,也逐渐被用来解决时间序列分类问题,文献[10-14]展示了深度学习方法对于时间序列分类的可行性,但在实际应用中也受到了一定限制,因为其需要大量的数据和复杂的计算量.
现实生活中大多数分类问题都属于不平衡分类的范畴,不平衡问题的研究来源于生活中现实问题的稀有事件,其难以发现但往往问题发生后又会产生严重的后果.如疾病诊断[15],诈骗检测[16],异常识别[17],自然灾害[18],癌症基因表达[19]等.解决不平衡问题有两个方向,一个是进行重采样,代表的有SMOTE(synthetic minority over-sampling technique)[20]算法.另一个是集成学习,boosting是其具有代表性的串行迭代方法.其中重采样只是单纯解决的数据不平衡的问题,忽略了数据空间时间关系,结果往往不理想.集成学习是将多个分类器集成在一起,每个分类器都对数据样本分类,用一定的规则来提高分类的精确性.
时间序列分类和不平衡数据常常会出现在同一个问题中,但将二者结合起来的研究成果还较少.随着深度学习的快速发展,出现了一批用深度学习来解决时序不平衡分类的方法,如论文[21]提出了一种自适应代价敏感卷积神经网络来解决时序不平衡,文中采用代价敏感网络(CS-CNN),用类相关矩阵对错分类样本进行惩罚.论文[22]提出一种基于对抗网络的异常序列检测方法,训练了一个编码器-解码器-编码器三子网发生器,该发生器只会从正常样本中提取特征,忽略了样本不均衡的问题. 因而,文中采用LSTM全卷积网络结合混合采样算法(SKLF算法)来对时序不平衡问题进行处理,此方法兼顾了时间序列和类不平衡的问题.
1 SKLF模型
1.1 SKLF混合模型
SKLF(SMOTE and K-means LSTM-FCN(并行))模型由混合采样和LSTM全卷积网络构成,模型训练流程框图如图1所示.混合采样由K-means和SMOTE组成,分别对多样本类进行欠采样和少样本类进行插值处理.
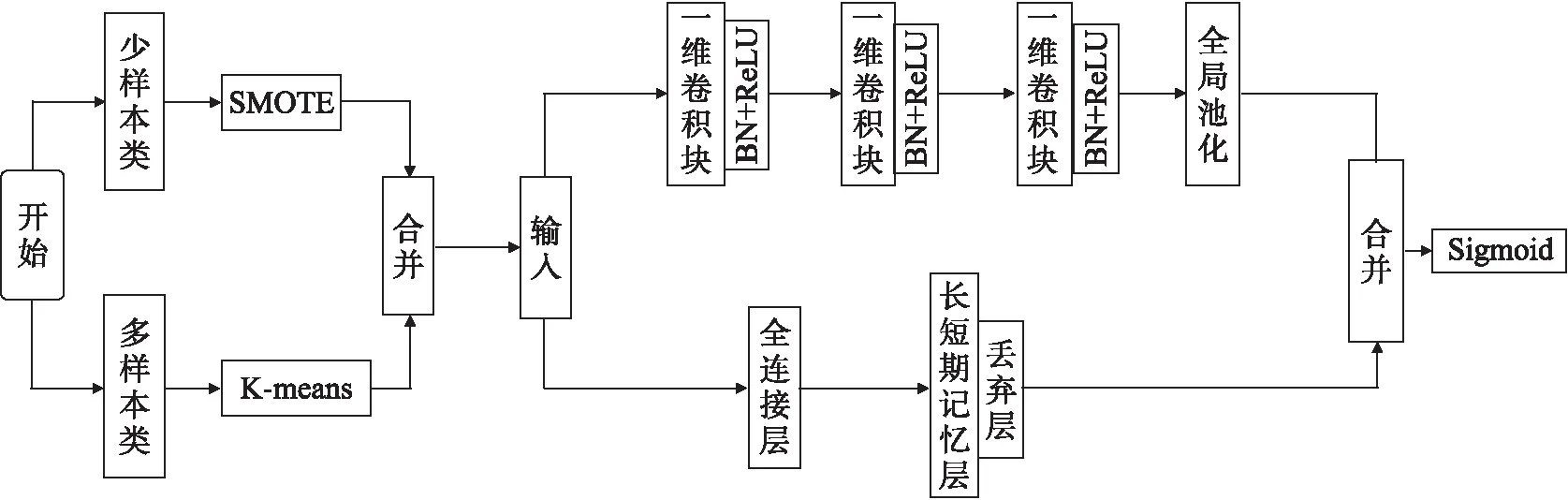
图1 SKLF模型训练流程框图
全卷积块由滤波器个数分别为128、256、128的3个堆叠时间卷积块组成.每个卷积块与王等[23]提出的CNN体系结构中的卷积块相同.每个块由一个时间卷积层组成,它伴随着批量归一化[24],随后是ReLU激活函数.最后,应用全局池化可以减少过拟合.
1.1.1 SKLF参数设置
SKLF网络中的超参数会对模型的训练和泛化能力有较大的影响.因此对超参数的设置比较重要,常见的参数设置方法一般有试验法、网格搜索法、遗传算法[25]等.基于一些通用的设计准则[26-28]利用试验法找到最佳参数并使 SKLF 网络稳定,具体参数设置如表1.其中,Nfilters表示卷积层滤波器的个数,Cs表示卷积核的尺寸,a表示激活函数,Nunits表示神经元数量.采用 Adam 优化算法,训练阶段损失函数采用mse,准确率使用binary_accuracy函数,一共训练20轮,每批次训练32个样本.
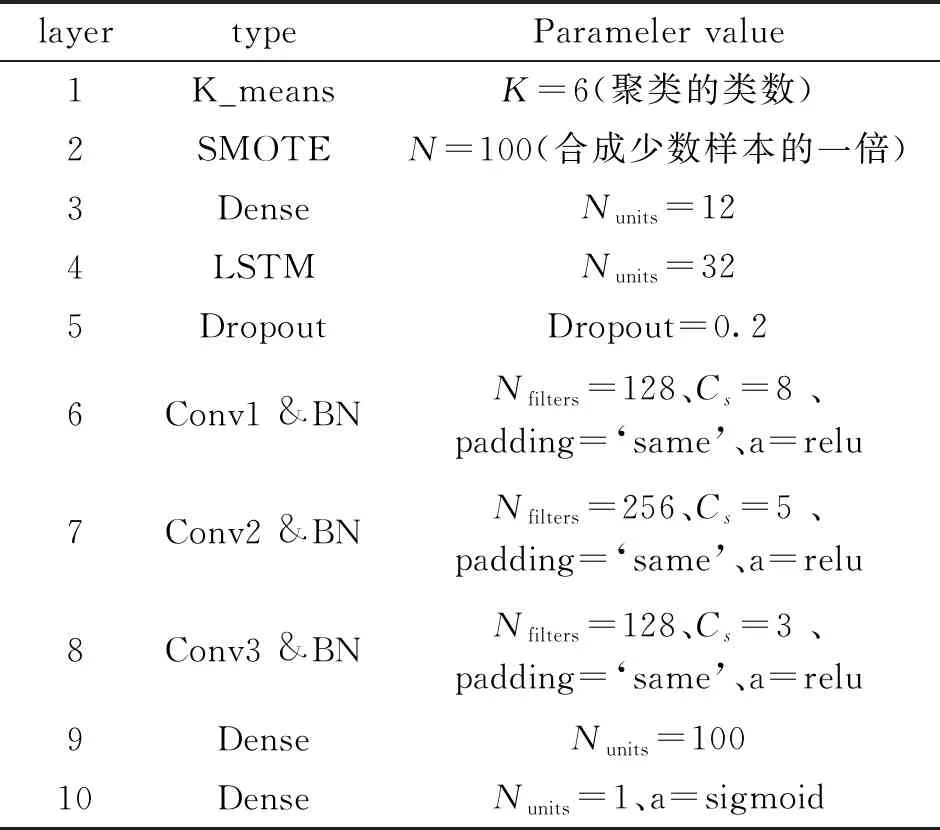
表1 SKLF网络参数设置
1.1.2 SKLF模型评价方法
在二分类问题中常用混淆矩阵来对模型进行评估,将真实类别与预测的类别划分成真正例(TP),假正例(FP),真反例(TN),假反例(FN)这4种情况,分类指标定义如下:
F-measure值(F):是精确率和召回率的调和均值.
(1)
G-mean值(G):同时考虑了正例和反例的准确率.
(2)
AUC值:表示ROC曲线下的面积大小,值越大,代表分类器性能越好.
(3)
其中,ranki表示第i个样本的序号(按从小到大排列),M和N分别表示正负样本的个数.
统计假设检验可以对几个分类器性能的优劣提出一个判断依据,因此在对比实验是可以采用假设检验来判断分类器模型的优劣,文中采用wilcoxon秩和检验,其相关原理如下:
记假设检验:
H0:算法A和算法B相近,没有统计意义上的显著差异
H1:算法A和算法B相近,有统计意义上的显著差异.
根据上述R的观察值r1,在给定的显著水平α下(α为0.05),H的拒绝域为:
r1≤C-U(α).
(4)
式中,临界点C_U(α)满足P{R_1≤C_U(α)≤α}的最大整数,只要知道R的分布,式子C_U(α)的临界点便可以求出,这里采用仿真法来获得R的分布,用python中的scipy包的stats.mannwhitneye()来计算秩和检验.通过对界值α比较来判断是否拒绝原假设H0
1.2 不平衡数据处理——混合采样
1.2.1SMOTE算法
SMOTE算法[20]是一种基于线性直插的方法,合成的主要方式是选取某个少数类样本和这个少数样本邻近样本的差值,并将差值与(0,1)间的某个随机数相乘,将所得结果累积在先前选定的样本上,此过程将少数类样本与其邻近连线的某点作为生成样本,可以有效的解决因简单复制少数类带来的过拟合问题.
SMOTE的基本原理为:取出训练样本S中少数类样本元素xi,先计算这个少类样本的同类k-邻近集pi,一般SMOTE算法中k的取值不超过10.然后,从pi中随机选择一个样本,设为xa,则少数类样本xi与同类样本k-邻近集合pi中的对应属性q上的差值记为diff(q)=xaq-xiq.最后,新合成的少数类样本fiq的数学表达式如下所示.
fiq=xi+(xaq-xiq)×rand(0,1).
(5)
式子中,rand(0,1)表示区域(0,1)中的随机数.
1.2.2 基于K-means的欠采样
时间序列是有顺序的一串单维或多维的数据,因此在处理时序不平衡数据时,不能简单的进行随机采样,要使用能保持其逻辑顺序的采样方式.因此采取基于聚类的不等比例欠采样的方法.首先采用K-means算法将多类数据聚合成K个类,这个K是一个超参数,可以用肘部法则(SSE)寻找一个最优的K值.然后根据这K个类中数据量的大小进行不等比例欠采样,这样既可以保留这些数据潜在的前后逻辑关系,又可以不破坏数据的结构.
SSE的核心指标是误差平方合,其计算公式如下:
(6)
上面式子中的i表示的是第i个簇,p是中的样本点,是的质心.
1.3 全卷积网络(FCN)和长短期记忆网络 (LSTM)
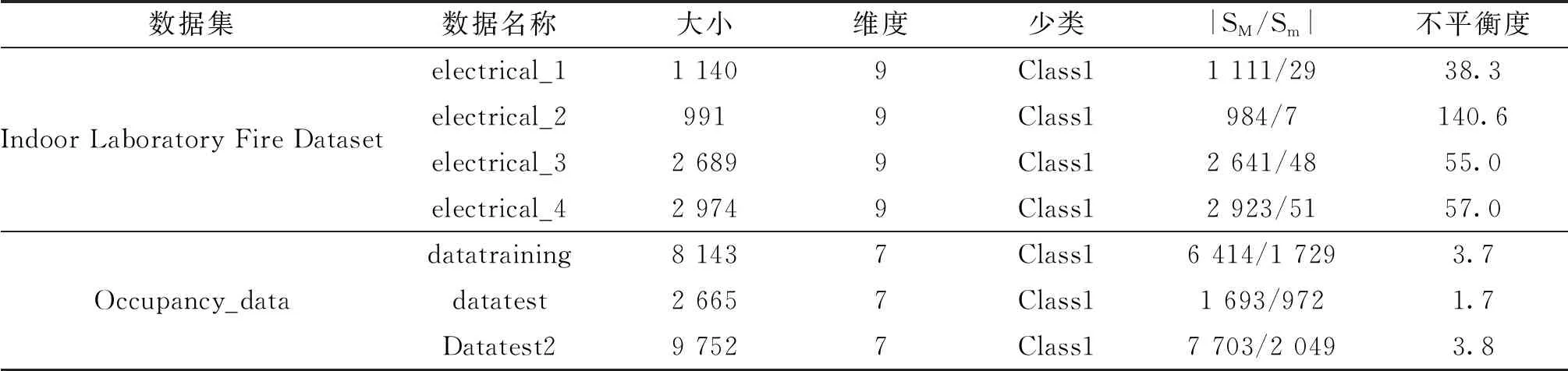
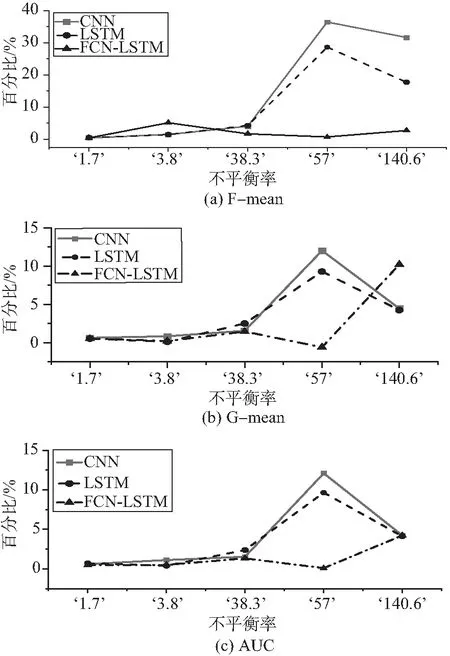
时间全卷积网络的输入是时间序列信号.如Lea等[29]所述,设Xt∈R^(Fo)是0 考虑L层一维卷积层.在这每一层上应用一组1D滤波器来查看输入信号如何演变的.根据Lea等[29]每个层的滤波器由张量(W^l∈R^(Fl×d×F_(l-1)))和偏差b_(l∈)∈R^(Fl)参数化,其中l∈{1,…,L}是层索引,d是过滤持续时间.对于第l层,(非标准化)激活(E_(i,t)^((l))∈R^(Fl))的第l个分量是来自前一层的输入(标准化)激活矩阵(E^((l-1))∈R^(F_(l-1)×T_(l-1)))的函数. LSTM[30]模型是循环神经网络(recur-rent neural networks,RNN) 结构中一种,可以对时间序列(TS)进行建模,通过一个记忆单元来储存任意时刻的值,便能记忆TS前后的关系.同时LSTM也具有删除和添加信息到细胞状态的能力,可以决RNN中存在的梯度消失或者梯度爆炸的问题.LSTM网络中记忆单元的结构如图2. 图2 LSTM神经单元结构图 记忆单元主要由输入门,遗忘门,输出门构成,输入门it是来决定添加信息的过程,遗忘门ft是决定失去一些信息,输出门ot是根据判断条件来输出当前记忆单元的一些状态特征.其计算公式如下: ft=σ(Wf[ht-1,xt]+bf) (7) it=σ(Wi[ht-1,xt]+bi) (8) (9) (10) ot=σ(Wo[ht-1,xt]+bo) (11) ht=ot×tanh(Ct) (12) 为验证本文所提算法SKLF的性能,采用2个数据集来进行实验并与单独LSTM、CNN和LSTM-FCN算法进行比较,一个数据集是来自实验室火灾数据集.该数据集包含8个受控火灾实验相关的时间系列数据,对于每个实验,都会记录湿度、温度、MQ139、TVOC 和 eCO2的传感器测量结果,文中采用其中4个电火源数据进行试验.另一个数据集是occupancy_data[31]数据,这个数据集描述的是一个房间内是否被占用的一个二分类问题.以下是2个数据集的描述. 在Indoor Laboratory Fire Dataset数据集中,采用electrical_3做训练集,其余数据做测试集.在Occupancy_data数据中,datatraining做训练集,其余数据做测试集,对测试的结果取10次平均值并分别和CNN、LSTM、FCN-LSTM比较. 表格3~5展示了4种算法分别在Indoor Laboratory Fire Dataset和 Occupancy_data数据集上的F-mean,G-mean,AUC分数,分析可以得到以下几条结论. 1) 表3中可以发现,SKLF算法在以上5个数据集上的F-means得分总体比较稳定,最高98.5%,最低为91.0%,平均得分为96.8%.F-means是精准率和召回率的调和平均数,可以看出SKLF模型在精准率和召回率上的性能都优于其他几种模型. 2) 从表4中可以发现,在5个数据集的不平衡率相差很大的情况下,SKLF算法模型在G-meas指标上波动很小,更加平稳.可以看出,模型的鲁棒性较高,在不同的不平衡率下也有不错的性能,适用性较强. 3) 从表5中总体来看,几种算法在5个数据集上的表现都还不错,得分基本上都达到了90%以上,但平稳度不如SKLF算法,其中CNN模型的波动最大,LSTM次之,FCN-LSTM稍次之.这是因为采用的5个数据集在样本的数量有较大的差别.因此,SKLF算法在数据量差异较大的情况下,也有不错的表现. 表2 数据集信息描述 表3 算法“SKLF”和其他算法的F-mean 表4 算法“SKLF”和其他算法的G-mean 表5 算法“SKLF”和其他算法的AUC 图3 SKLF算法相对其他算法的性能增加率和不平衡率的关系 从表6中的Wilcoxon检验可以看出,SKLF算法相对LSTM可以提高上述3种指标的分数,说明SKLF模型在处理时间序列不平衡分类上的性能要优于LSTM模型.对于CNN,SKLF算法在保持F-means值不变的情况下,提高了G-means和AUC的值.相对于FCN-LSTM算法,SKLF算法与其的区别在于FCN和LSTM的结构上,FCN-LSTM是串行结构,而SKLF模型中FCN和LSTM为并行结构,可以得到模型的网络结构对其性能也有一定的影响,并行的SKLF模型在处理时序不平衡分类时要优于串行的FCN-LSTM. 表6 算法“SKLF”和其他算法的Wilcoxon检验 通过分析图3与图4可以得到以下结论: 图4 SKLF算法和其他算法的指标平均值 1) 算法SKLF相对CNN,LSTM,FCN-LSTM,能够显著提高平均AUC,F-means和G-means 的值. 2) 当不平衡率大于38.3时,SKLF算法能显著提升所有数据集的评价指标,特别是F-means和G-means的值. 3) 从评价指标的平均值来看,4种算法对时序不平衡分类的处理能力由大到小依次为SKLF>FCN-LSTM>LSTM>CNN.由此可以看出,SKLF组合算法,实现了几种算法的优势互补,对问题的处理能力相较于单个算法要强,鲁棒性要高. 文中提出了集时序不平衡和时空特征提取为一体的SKLF算法解决了结构复杂、高噪音、不平衡的时间序列分类问题,相较于传统的分类算法有一个较好的分类结果.通过结合过采样和欠采样,将不平衡数据中的多类样本采用K-means不等比采样,保证了多类数据前后的结构关系,将少类数据采用SMOTE过采样,使2类数据的不平衡率降低,然后组成训练数据,并将FCN和LSTM算法的优势相结合,将训练数据分别导入全卷积网络和长短时记忆网络,让其各自进行训练,在送入sigmoid函数输出前将二者结合,得到最终的分类结果.通过在Indoor Laboratory Fire Dataset和Occupancy_data数据集上的对比实验,表明 SKLF 算法对时序不平衡的分类精度达到了98.5%,且性能比较稳定,有较好的鲁棒性.相较于CNN,SKLF算法将评价指标的平均值提高了4%~10%.相较于LSTM和FCN-LSTM,SKLF算法将评价指标的平均值分别提高了1%~5%和1%~3%.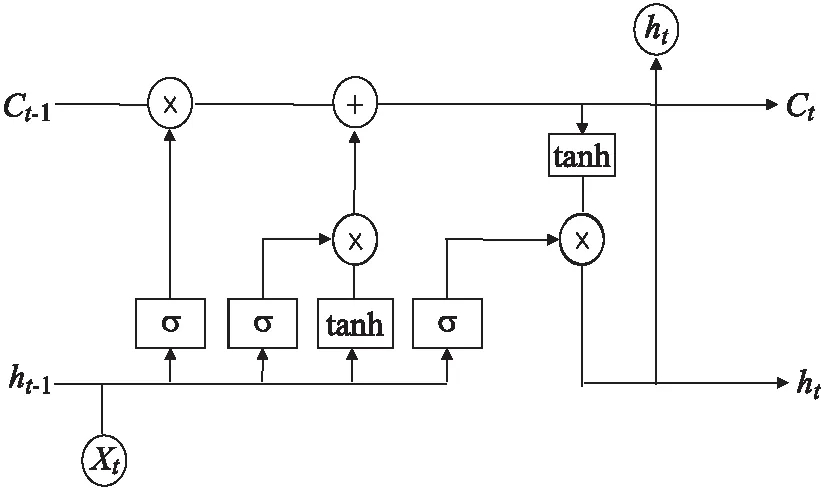
2 实验结果分析





3 结语
