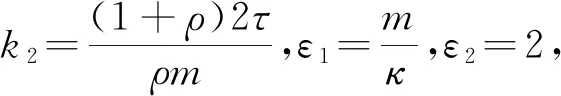一类波板方程组的空间衰减估计

石金诚，肖胜中

(1.广州华商学院 数据科学学院，广东 广州 511300； 2.广东农工商职业技术学院 科研处，广东 广州 510507)

Saint-Venant原理在数学与力学中有着广泛的应用，而解的空间指数衰减估计是Saint-Venant原则的一个重要性质，在研究解的Saint-Venant原则时，需要添加一个解在无穷远点处趋于零的限制.近年来，许多学者开始研究解的空间衰减估计或Phragmén-Lindelöf二择一结果.经典的Phragmén-Lindelöf定理指出:调和方程的解从圆柱面有限的一端到无穷远处必须随距离呈指数增长或指数衰减.后来, Payne 和Schaefer[1]将研究由调和方程推广到双调和方程上来, 得到了双调和方程在3个不同区域的Phragmén-Lindelöf二择一结果. 文献[2-5]利用各种方法研究了双调和方程的空间性态. 对于与时间相关的双调和方程的解的性态研究可见Liu等[6]，作者采用二阶微分不等式的方法得到与时间相关的Stokes方程的Phragmén-Lindelöf二择一结果. 上述文献所考虑的方程均是单个方程, 由于双调和方程研究的难度较大, 导致研究双调和方程组的文献较少.

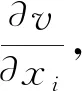
1 问题描述

在如下无界区域Ω0内考虑，其中Ω0为

Ω0={(x1,x2)|x1>0,0

(1)

其中h是一给定的正常数.同时引入下面的记号

LZ={(x1,x2)|x1=Z≥0,0≤x2≤h}.

(2)

在文献[14]中，作者采用C0-半群方法，研究了如下含有热现象波板系统方程组解的分析性态.

ρ1utt-Δu-μΔut+λΔv=0,

(3)

ρ2vtt+γΔ2v+λΔu+mΔθ=0,

(4)

τθt-κΔθ-mΔvt=0,

(5)

其中u表示弹性模的垂直扰度，v表示弹性板的垂直扰度，θ表示温度差，ρ1,ρ2,μ,λ,κ,γ,τ,m均为非负数，Δ表示Laplace算子，Δ2表示双调和算子.上述模型可以用来描述由弹性膜和弹性板组成的系统板的演化过程.

文中考虑(3)～(5)系统中当λ=0的情形，由于此时u未与其他方程耦合,因此考虑如下双曲抛物耦合系统.

ρvtt+γΔ2v+mΔθ=0,

(6)

τθt-κΔθ-mΔvt=0.

(7)

方程(6)和(7)满足如下初边值条件：

(8)

gi(x2,t),i=1,2,3是给定函数并满足如下的相容性条件：

(9)

此外，解在无穷远处添加如下限制条件：当z→∞时，

v,vt,vα,vαt,vαβ,vααβ,θ,θα→0.

(10)

本文,得到双调和方程组 (6～7)的解在条件(8～10)下的空间衰减估计.

2 能量表达式 φ(z,t)

首先需要推导出能量表达式.

在式(1)两边同时乘以exp(-ωt)vt并积分，可得

(11)

定义函数φ1(z,t)如下：

(12)

联合式(11)和(12)，可得

(13)

在式(7)两边同时乘以exp(-ωt)θ并积分，可得

(14)

定义函数φ2(z,t)如下：

(15)

联合式(14)和(15)，可得

(16)

在式(7)两边同时乘以exp(-ωt)vt并积分，可得

(17)

定义函数φ3(z,t)如下：

(18)

联合式(17)和(18)，可得

(19)

在式(6)两边同时乘以exp(-ωt)θ并积分，可得

(20)

定义函数φ4(z,t)如下：

(21)

联合式(20)和(21)，可得

(22)

在式(6)两边同时乘以exp(-ωt)vαα并积分，可得

(23)

定义函数φ5(z,t)如下：

(24)

联合式(23)和(24)，可得

(25)

定义一个新的能量函数φ(z,t)：

(26)

其中k1,k2是大于零的任意常数.

3 空间衰减估计

这一节将得到如下的空间衰减估计：

定理1假设(v,θ)为初边值问题(6～9)的经典解，则

其中，E(z,t)是大于零的函数，k3是大于零的常数.

证明联合式(12)和(15)，可得

(27)

由式(18)和(21)，可得

(28)

由式(24)，可得

(29)

式(28)，由Schwarz不等式，可得

(30)

其中ε2是大于零的任意常数.

式(29)，由Schwarz不等式，可得

(31)

联合式(26)、(27)，(30)和(31)，可得

(32)

在式(32)中，取

(33)

联合式(13)，(16)，(19)，(22)和(25)，可得

(34)

式(34),由Schwarz不等式和式(33)，可得

(35)

其中k3为可计算的大于零的常数.

式(35)，可写为

(36)

积分式(36)，可得

(37)

其中φ(0,t)可以通过初始数据来控制,省略其估计过程.

由式(33)，可知

(38)

由式(37)和(38)，可得

(39)

式(39)即是所需的空间衰减估计.