双偏振降水估测算法在三种降水中的性能评估

张弘豪，陈时东，郭泽勇，陈星登，曾广宇

（1.阳江市气象局，广东阳江 529500；2.阳春市气象局，广东阳春 529600 3.阳江市海陵试验区气象局，广东阳江 529500）

20世纪80年代法国、德国、英国、澳大利亚、日本等国都相继发展了自己的偏振雷达，90年代偏振雷达技术和应用研究得到了进一步发展。2000年，双偏振雷达技术开始从研究向业务应用转移，以提高目前对降水类型等的天气预报能力。2011年，美国在现有的WSR-88D雷达系统基础上加装双线偏振技术，并在2013年完成了NEXRAD偏振雷达改造，应用于气象观测业务。2014年，中国开始在业务多普勒天气雷达上加装双偏振功能，其中广东、上海等地率先完成雷达加装升级改造。天气雷达双偏振升级后，增加的差分反射率、差分传播相移、差分传播相移率及相关系数等偏振参量观测为定量降水估测和微物理参数反演等提供了更多信息［1-3］。随着双偏振多普勒天气雷达的快速发展及其在云降水领域的广泛应用，双偏振雷达的偏振参量极大提高了降水估测及水凝物分类识别的能力［4-5］。

当前，关于双线偏振雷达降水估测算法的研究已取得了一些进展和突破，张羽等［6］分析了不同算法对不同雨强的估测能力；王建林等［7］对不同偏振量的降水估测效果进行对比分析；刘黎平［8］对比分析了双偏振和单偏振的降雨估测能力，但对不同偏振参量在不同类型降水系统中的估测能力研究较少，因此，本研究在目前国内广泛应用的经典CSU-HIDRO算法基础上，利用广州S波段双线偏振雷达数据和地面自动站雨量数据，针对R（ZH）、R（ZH，ZDR）、R（KDP）、R（KDP，ZDR）及复合算法R（C）等降水估计关系在台风、季风和锋面3种不同降水系统中的估测效果进行评估和检验，通过分析不同估计关系在不同类型降水系统中的表现，为研究适合不同降水系统的降水估测方案提供技术参考。

1 数据资料

1.1 降水过程

本研究选取2017—2020年广东珠三角地区几次典型的台风、季风和锋面降水过程进行估测算法的评估和检验，降水概况如表1所示。

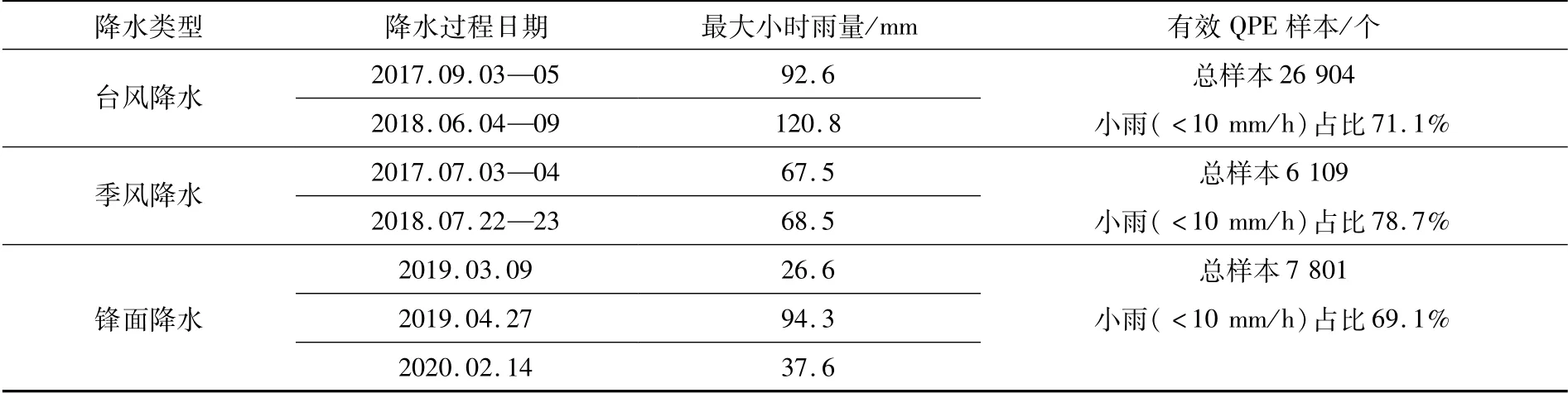
表1 降水过程概况

1.2 雷达和雨量计数据

广州新一代天气雷达CINRAD／SA于2016年初完成双偏振雷达升级改造并投入业务使用，均采用VCP21体扫模式，是国内首批业务化使用的双偏振雷达，迄今为止积累了4年多的灾害性天气过程数据。本研究选取广州雷达1.5°仰角体扫数据的定量降水估计（QPE）样本和雷达120 km径向扫描圈内的区域自动站小时雨量数据（Gauge）进行对比评估，其站网分布如图1所示。

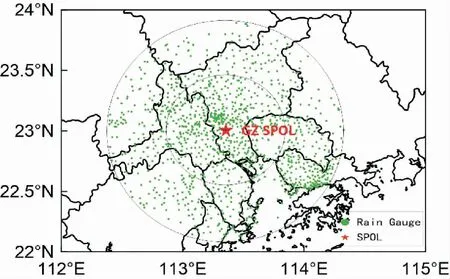
图1 站网分布图

2 数据处理与评估

2.1 数据处理

雷达和自动站数据在使用前需进行数据质量控制。关于双偏振雷达数据质量控制的研究，业界已有相关学者做了一些研究，大部分都是对于双偏振雷达特有的偏振量进行一些质控的算法。本研究数据质量控制方法主要有非气象回波识别与剔除［9］、双偏振雷达系统差分反射率误差订正［10］及处理差分传播相移的方法［11］。地面数据质量控制采用了时间、空间一致性检查的方法［12］。

2.2 定量降水估测算法

由于双偏振雷达偏振参量的特点和特殊优势，双偏振雷达定量降水估测算法相对于传统单偏振PPS算法具有较强的估测优势。本研究选取美国对于液态降水估测的CSU-HIDRO经典算法［10］，具体流程如图2所示。

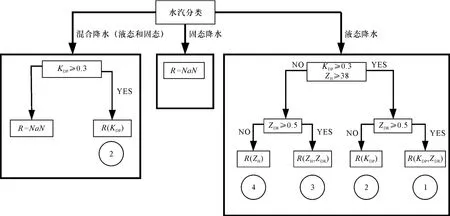
图2 CSU-HIDRO算法流程示意图

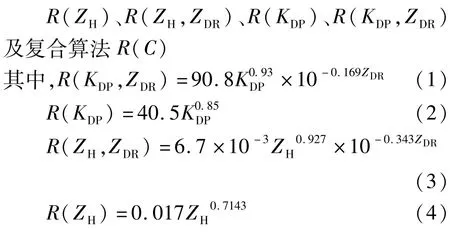
2.3 评估指标

为对不同估测算法在3种类型系统降水中的估测效果及降水区间进行定量分析，选取均方根误差（RMSE）、相对误差（RE）、归一化误差（NE）、相关系数（CC）作为检验指标。其中QPE／Gauge比值越接近于1表示雷达估测值与实况越接近；均方根误差反映了雷达估测值和雨量计实测值之间的离散程度（mm），其值越小离散程度也就越低；归一化（NE）的绝对值越低表示误差越小（%），相对误差RE与NE的区别在于可以判断估测是高估还是低估，正值为高估，负值为低估。相关系数（CC）为量纲一的量，表示了估测值和实测值之间相关关系密切程度，其值越接近于1表示相关程度越高。

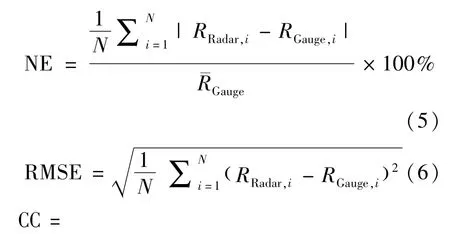
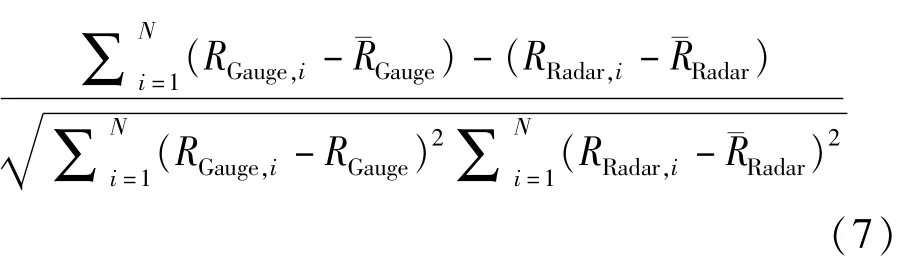
其中，RRadar为自动站点的雷达定量估测雨量值（mm）；RGauge为自动站点实际雨量观测值（mm）；N为雷达-雨量计匹配数据点样本数。

3 数据分析

根据第2章评估检验算法和评估指标对3类系统降水的不同估测算法进行分析，其估测数值如表2所示。以下将用RE、NE、RMSE及CC来评估不同系统、不同降水估测算法的效果。

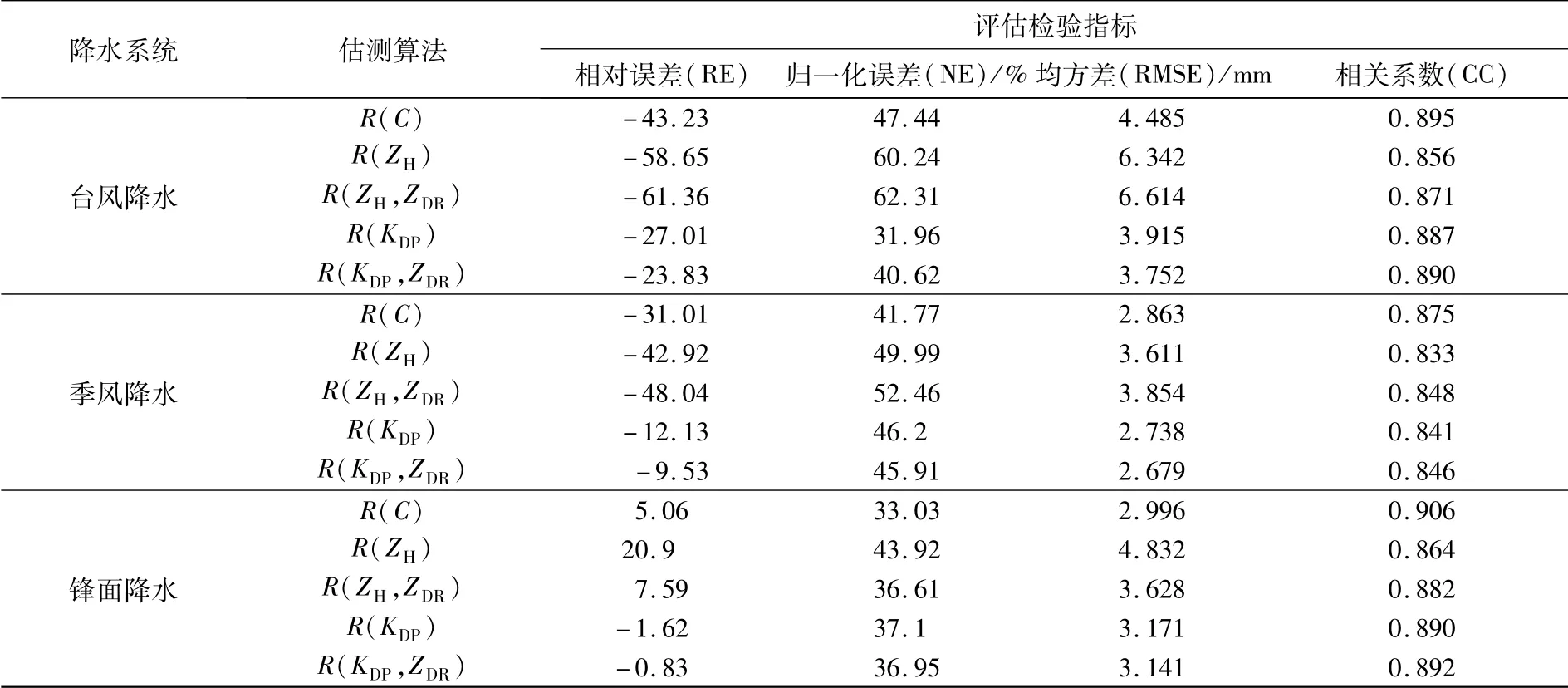
表2 三类降水系统估测效果对比

3.1 复合算法R（C）整体检验

如表2所示，在3类系统中，台风降水和季风降水中R（C）的NE分别为47.44%和41.77%，高于锋面降水中的33.03%，表明复合算法R（C）在锋面降水系统中的表现最优。从RE、RMSE及CC来看，与NE的表现整体匹配；从复合算法R（C）的估测值与实况雨量的散点分布（图3）来看，台风和季风降水估测值大多低于实况值，存在明显的低估；而锋面降水系统的估测值与实况雨量的散点分布更为集中，表明估测值与实况值最为接近。

图3 估测小时雨量与实测小时雨量散点图

表2中台风和季风降水的RE分别为-43.23%和-31.01%，锋面降水则仅为5.06%，散点图分布与估测指标完全一致。总体上，3种降水系统中，台风降水的QPE性能表现最差，季风次之，锋面最好，这与选取的天气个例有关。台风降水中小雨样本偏多，所以误差偏大；而锋面降水个例的大雨样本较多且风速小，因而整体估测效果优于台风和季风系统。

3.2 单一降水估计关系在不同降水系统中的估测效果对比

对比分析4个单公式算法在不同类型降水系统中的表现（表2）发现，从NE指标看，3种降水系统中，R（KDP）在台风降水系统的NE指标仅为31.96%，明显低于季风的46.2%和锋面的37.1%；通常而言，由于加入ZDR特征量的原因，R（ZH，ZDR）的估测性能应该优于R（ZH）：3种降水系统中，锋面降水符合这一规律特征（36.61%＜43.92%），但在台风和季风系统中却与之相反（62.31%＞60.24%，52.46%＞49.99%）。

以上结果表明单一降水估计关系在不同系统的表现存在较大的差异，在台风和季风系统中，引入极化变量ZDR后的估计关系R（ZH，ZDR）的估测性能反倒不如单偏振估计关系R（ZH），这与不同降水系统具备的特殊微物理特征有关，比如台风系统风力大、携带水汽充沛，使得降雨粒子多为粒子浓度高的小雨滴，而KDP在表征强降水和粒子浓度方面有着特殊优越性，这可能会导致台风的R（KDP）性能优于其他两种系统，同时由于选取的台风和季风个例的风力较强的关系，导致ZDR产生较大的形变而带来更大的ZDR误差，所以造成R（ZH，ZDR）的估测性能反倒不如R（ZH）。

3.3 复合算法R（C）与单一降水估计关系的性能对比

双偏振量ZDR和KDP能更精细表征降水粒子的微物理特征，因此无论在哪一种天气系统中，由于引进这两个特征量之后，双偏振雷达复合降水估测算法R（C）的估测性能均优于单偏振降水估测算法R（ZH）：台风系统中R（C）的NE（47.44%）优于单R（ZH）的60.24%；季风系统中R（C）的NE（41.77%）优于单R（ZH）的49.99%；锋面系统中R（C）的NE（33.03%）优于单R（ZH）的43.92%。另外，在台风系统中，R（C）的NE反倒不如R（KDP）的31.96%和R（KDP，ZDR）的40.62%。结果表明，复合算法R（C）和4个单一降水关系在不同降水系统中的适用性存在明显不同，其原因在于不同天气系统具备不同的微物理特征，因此有必要针对不同天气系统建立双偏振雷达的本地化QPE算法。

4 结论

1）4种单一降水估计关系在不同系统表现出较大的性能差异，这主要与选取降水个例的微物理特性有关。其中选取的台风和季风降水个例中，由于较大的风速导致降雨粒子产生形变，进而导致较大的ZDR误差。因此在台风和季风系统中，引入极化变量ZDR后的估计关系R（ZH，ZDR）的估测性能反倒不如简单的单偏振估计关系R（ZH）。

2）由于复合算法R（C）能综合利用单一估计关系的优势，因此一般情况下R（C）的估计性能均优于R（ZH）、R（ZH，ZDR）、R（KDP）及R（KDP，ZDR）4种单一估计关系，这在季风降水和锋面降水系统中得以体现。但在台风降水系统中，R（C）的估计性能低于R（KDP）和R（KDP，ZDR）；在不同系统的横向对比中发现，R（KDP）关系在台风降水中的表现明显优于锋面和季风系统，这是由于台风具备风力大、水汽充沛，使得降雨粒子多为粒子浓度高的小雨滴，而KDP在表征强降水和粒子浓度方面有着特殊优越性，这会导致适用于台风降水的QPE流程中偏振量阈值区间的设定与经典CSU-HIDRO算法存在区别，这可以解释台风系统中估计算法表现出的性能差异原因，同时也说明有必要建立适合台风降水系统的双偏振雷达降雨估测方案。

3）双偏振量ZDR和KDP能更精细的表征降水粒子的微物理特征，因此无论在哪一种天气系统中，双偏振雷达复合降水估测算法R（C）的估测性能均优于单偏振降水估测算法R（ZH）。但复合算法在不同降水系统中的差异性非常明显，本研究选取的锋面系统降水个例的大雨样本较多且风速小，因而整体估测效果优于台风和季风系统。由于不同天气系统具备的微物理特征存在明显差异，表明了针对不同天气系统建立本地化QPE算法的必要性。