基于等效夹杂理论的混杂纤维复合材料有效弹性模量预测

秦飞飞，盛冬发

(西南林业大学土木工程学院,昆明 650224)

混杂纤维增强复合材料(HFRCs)是指在基体中添加两种或两种以上纤维的新型复合材料,该材料从20世纪70年代开始发展起来[1-2]。由于混杂纤维复合材料同时具备不同纤维的优良特性,在航空航天、建筑材料、汽车制造、纺织工业等领域得到广泛应用。

20世纪90年代开始,随着人们生态环境保护意识的提高,科研人员逐渐使用天然纤维替代部分人造纤维应用于混杂纤维增强复合材料。Petrucci等[3]采用玄武岩纤维、亚麻纤维、大麻纤维和玻璃纤维为增强纤维,取其中两种增强纤维与环氧树脂制成三相混杂复合材料,研究了混杂复合材料的冲击性能。Li等[4]以钢纤维、聚乙烯醇纤维和碳酸钙晶须为增强相制备混杂纤维增强水泥基复合材料,研究发现钢-聚乙烯醇纤维-晶须的加入缓解了复合材料的受压开裂。Calabrese等[5]研究了环氧树脂/玻璃纤维/亚麻纤维混杂复合材料在恶劣环境下的耐久性。研究表明加入玻璃纤维可以显著提高亚麻纤维/环氧树脂复合材料层压板在海洋环境条件下抗老化性。Ghori等[6]研究了椰枣纤维和洋麻纤维增强环氧杂化复合材料的热性能和力学性能。结果表明,复合材料的挠曲模量随洋麻比增高而增大。Xun等[7]通过对玻璃/碳纤维增强塑料复合材料进行水热环境下拉伸性能测试,讨论了温度、层厚度、层角度对拉伸强度的影响。Khalid等[8]对不同重量百分比的玻璃纤维和黄麻纤维增强环氧复合材料进行了冲击性能试验,研究发现黄麻纤维比玻璃纤维对复合材料冲击强度的贡献更大。徐虹等[9]制备了不同碳纤维和玄武岩纤维(BF)含量的混杂增强树脂基复合材料,通过有限元模拟确定了混杂纤维复合材料刚度、强度和拉伸极限应变最大时的混杂比。

目前,国内研究人员对混杂纤维复合材料力学性能研究主要侧重于试验及分析方面,而混杂纤维复合材料的细观力学研究相对较少。笔者将混杂纤维复合材料看作由两种不同纤维嵌入基体的三相复合材料,根据黄敏杰等[10]给出的等效夹杂原理和分步均匀化方法,提出可预测三相复合材料的拉伸弹性模量的细观力学模型。最后将此方法预测结果与文献中试验结果和有限元模拟结果进行对比,以此来验证笔者提出的细观力学模型的合理性。

1 混杂纤维复合材料有效弹性模量分析

基于等效夹杂理论,得出单一纤维及基体内的平均应力和应变,将其代入两相复合材料均匀化平均应力、应变表达式,从而求解出两相复合材料的有效弹性模量。最后采用分步均匀化方法将两相复合材料当作新基体,另一种纤维作为增强相,计算出三相混杂复合材料的有效弹性模量。

1.1 等效夹杂理论

在纯基体中加入与其弹性模量不同的夹杂体,并且受到远场均匀应变ε(∞)ij作用情况下,如图1a所示。由于夹杂体的存在,基体的平均应力、应变较均匀纯基体增加了扰动应力、扰动应变。含夹杂复合材料基体内的平均应变和应力为：

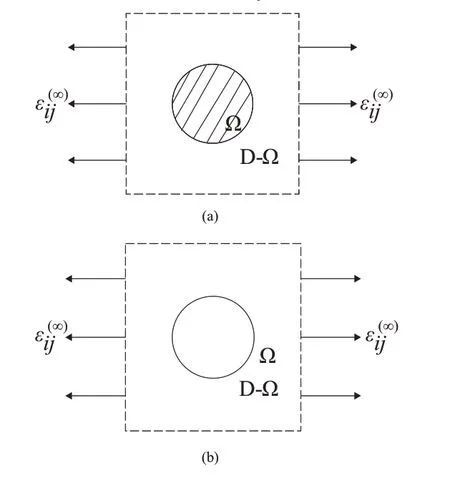
图1 复合材料夹杂均匀化

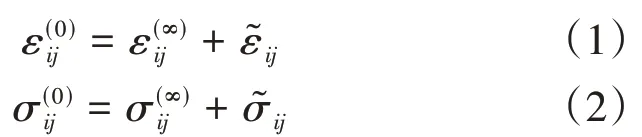
式中,ε(∞)ij为远场均匀应变为扰动应变,为纯基体受到的均匀应力为扰动应力。

由于基体与夹杂弹性性质的差别,在外力场作用下夹杂内的应力、应变与基体内的应力、应变不同,两者分别相差一个摄动值和,夹杂内的应变和应力分别为：

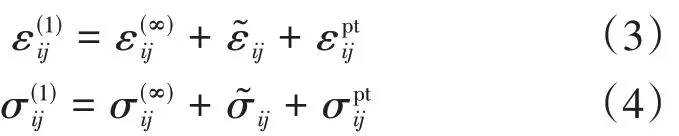
根据Eshelby等效夹杂理论[11],引入一个等效本征应变,夹杂的弹性常数转化为与基体相同的弹性常数,即：

式中,为纤维弹性常数,为基体弹性常数为等效本征应变。转化过程见图1所示。

摄动应变与等效本征应变的关系可以由Akamatsu的理论[12]得出：

式中,Sijkl为夹杂的Eshelby张量[13],与夹杂的形状和基体的泊松比有关。

根据混合率方法,复合材料平均应变和组分材料平均应变的关系式为：

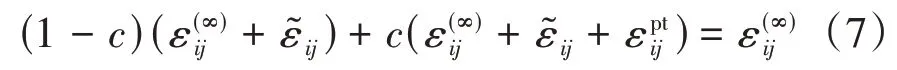
式中,c为夹杂的体积分数。

求解式(6)、式(7)可得：

联立式(5)、式(6)和式(8)可求得,根据式(1)～式(4)可得基体和夹杂内平均应力及平均应变。

1.2 两相复合材料有效弹性模量求解

复合材料视为由若干根圆柱形纤维(f)埋入基体(m)中,如图2所示。对复合材料施加纵向均匀应变边界条件,以获得复合材料有效弹性模量。由式(5)可得：

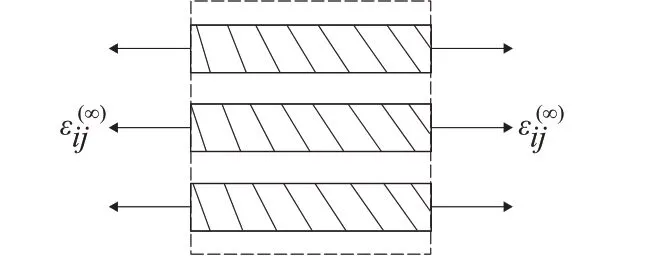
图2 复合材料在均匀应变边界条件作用

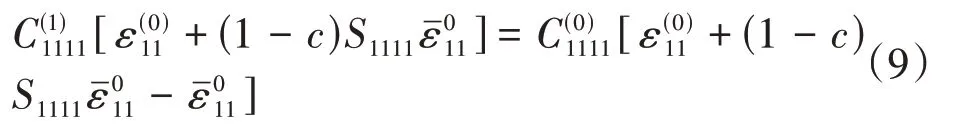
式中,为基体弹性常数,为纤维弹性常数,εˉ011为等效特征应变为施加的均匀应变边界条件。

求解方程(9),可得等效特征应变,将其代入式(1)～(4),即可求出纤维与基体的平均应力和平均应变。

纤维内的平均应力、应变分别为：

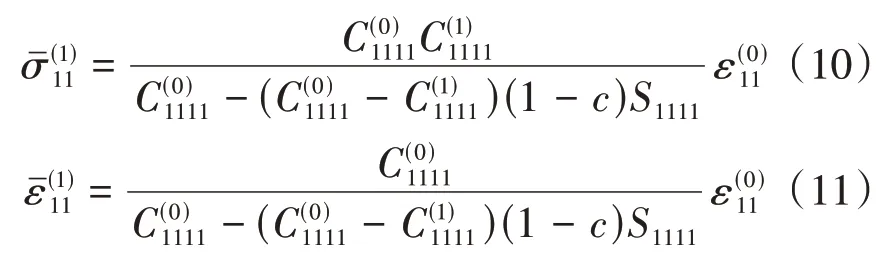
基体内的平均应力、应变分别为：

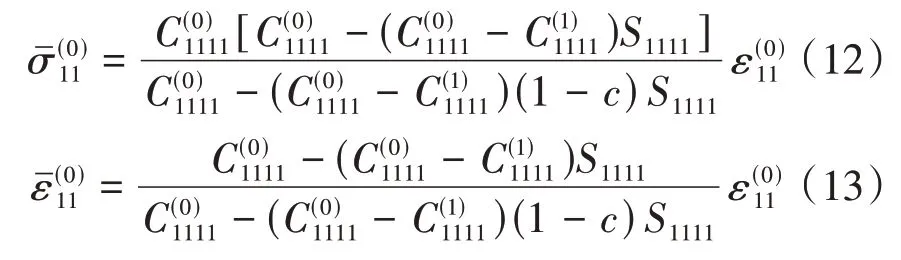
根据混合率方法得出两相复合材料的平均应力和平均应变分别表示为：

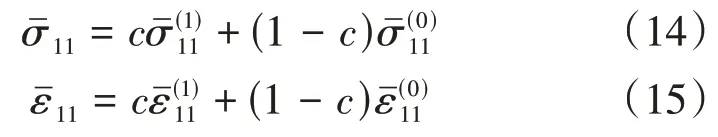
将式(10)～(13)代入式(14)和式(15),可得到两相复合材料的平均应力和应变,由此可得复合材料的纵向弹性模量,即：

式中,E11为复合材料的纵向弹性模量。

1.3 分步均匀化方法

混杂纤维复合材料属于多类夹杂问题,可采用分步均匀化方法处理每一类纤维材料[14],逐步计算出混杂纤维复合材料的有效性能。分步均匀化的步骤是：首先向基体材料(弹性模量Cijkl和泊松比ν等材料属性确定)中投入第一种纤维(设其弹性模量为),然后使用式(9)～(16)完成均匀化过程,得到均匀化复合材料的弹性模量,如图3a所示。用均匀化后的复合材料作为新的基体(其弹性模量为),投入另一类纤维(设其弹性模量为),再次使用式(9)～(16)进行均匀化,得到新的弹性模量,即为三相复合材料的有效弹性模量,如图3b所示。

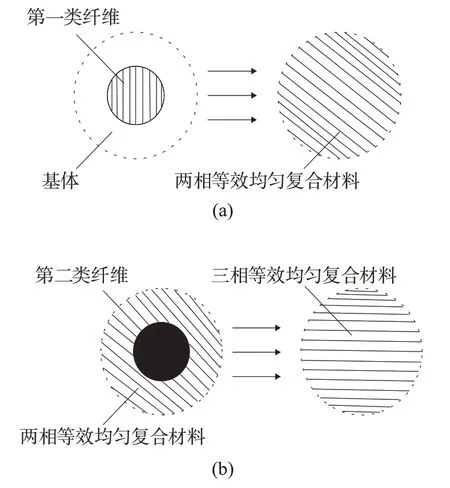
图3 分步均匀化示意图

1.4 算例验证

将细观力学模型计算结果与现有文献[15]中的试验结果进行对比,以验证本预测方法的正确性。其中,BF、剑麻纤维(SF)、聚乳酸(PLA)拉伸弹性模量分别为88.9,9.4,2.1 GPa,根据材料参数计算出Eshelby张量,将其代入式(9)～(16)解出不同SF质量分数下的两相复合材料纵向,预测结果与文献[15]试验值对比结果见表1。从表1可以看出,理论预测值与试验值较为接近,表明细观力学预测方法有较好的预测精度。

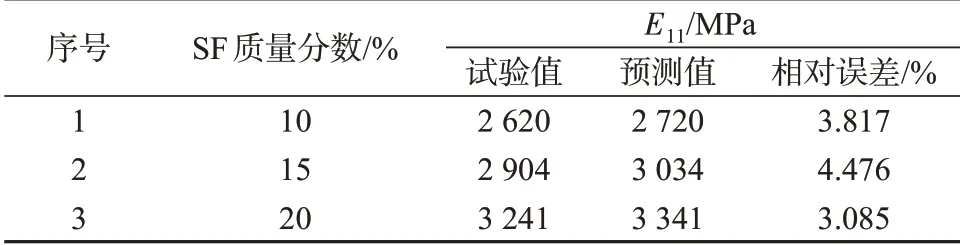
表1 不同SF含量的PLA复合材料拉伸弹性模量预测值与试验值

采用分步均匀化方法将剑麻纤维增强聚乳酸复合材料当作新基体,式(9)～(16)解出不同混杂纤维质量分数下的三相复合材料纵向拉伸弹性模量,预测结果与文献[15]试验值见表2。从表2可以看出,混杂纤维含量在27.27%以下时,预测结果与试验结果的相对误差基本保持在15.26%以内。混杂纤维含量达到33.33%时,预测值与试验值的误差较大为22.43%。因此,本方法在混杂纤维含量低于27.27%时可认为是较为有效的。

表2 不同混杂纤维含量时PLA复合材料纵向拉伸弹性模量预测值与试验值对比

2 预测值和有限元模拟对比

2.1 RVE尺寸参数

根据混杂纤维复合材料的增强纤维在基体中的分布具有统计学上的周期性,提出了复合材料在细观结构上具有周期性的假定[16]。使用ABAQUS有限元模拟软件建立剑麻纤维和BF沿纵向分布于聚乳酸矩形截面的代表性体积单元模型,代表性体积单元的长宽厚依次为0.58 mm×0.58 mm×0.60 mm,混杂纤维复合材料有限元模型如图4所示。

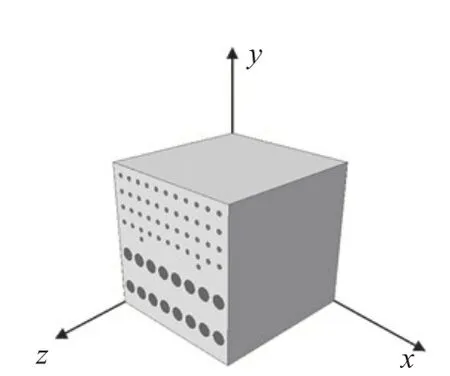
图4 纤维质量比1∶1的混杂纤维复合材料模型

2.2 模拟计算

采用ABAQUS软件对代表体积单元拉伸模拟,如图5所示。在三维有限元模型底面施加固定约束,限制模型底部位移和转动。顶部施加均匀位移边界条件,位移增量步为0.05。从后处理数据中提取代表体元横截面各点的应力和应变数值,并对提取的数据平均计算绘制出不同纤维质量分数下的应力-应变曲线,见图6。进而得出了混杂纤维复合材料的纵向拉伸弹性模量随纤维含量变化的情况。

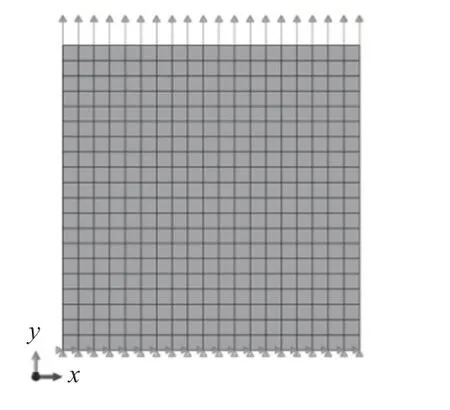
图5 混杂纤维复合材料有限元轴向拉伸模拟

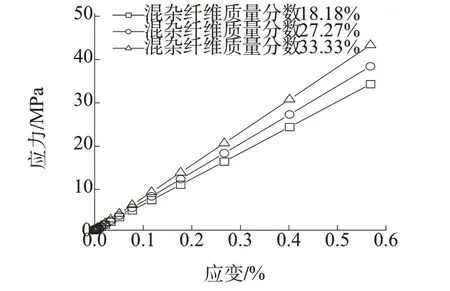
图6 不同混杂纤维质量分数的复合材料应力-应变曲线

2.3 预测值与模拟结果对比

将本方法预测结果与ABAQUS模拟结果和文献[15]的试验值绘制于图7。从图7可以看出,本方法预测值较ABAQUS模拟值更接近试验值。ABAQUS模拟值与试验值偏差较大,原因可能是混杂纤维复合材料制备时增强纤维和基体连接可能存在微观缺陷,而在有限元模拟中规定复合材料的纤维和基体黏结完好,从而造成模拟结果偏大。显然,本方法在预测三相混杂复合材料的拉伸弹性模量时预测结果更为精确。

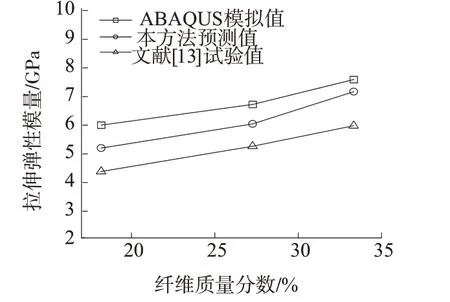
图7 混杂纤维复合材料拉伸弹性模量随纤维含量变化曲线

3 混杂纤维复合材料拉伸弹性模量影响因素分析

混杂纤维复合材料拉伸弹性模量的影响因素主要是混杂纤维的用量和混杂纤维的拉伸弹性模量。为分析以上因素对复合材料拉伸弹性模量的影响,以SF/BF混杂增强PLA复合材料为例,利用建立的细观力学模型预测混杂纤维复合材料的拉伸弹性模量。该预测方法为混杂纤维复合材料性能设计提供了一种新方法。

3.1 混杂纤维含量的影响分析

图8a、图8b分别为混杂纤维增强PLA复合材料拉伸弹性模量随BF,SF质量含量变化规律,图中f(SF)和f(BF)分别为SF,BF的固定质量分数。从图8a、图8b中可看出,保持一种纤维质量分数不变,混杂纤维增强复合材料的拉伸弹性模量随另一种纤维含量的增加呈线性方式增大。从图8a可以看出,随着SF用量的增加,混杂纤维增强复合材料的拉伸弹性模量也在逐渐增加,但是这种增加效果随BF用量增大而逐渐减弱。从图8b可以看出,随着BF用量的增加,混杂纤维增强PLA复合材料的拉伸弹性模量也在逐渐增加,并且这种增加效果随BF用量增大而逐渐减弱。比较图8a、图8b可以得出,混杂纤维增强PLA复合材料拉伸弹性模量随BF含量增加变化更为明显,即BF含量变化对混杂纤维增强复合材料拉伸弹性模量的影响大于SF。

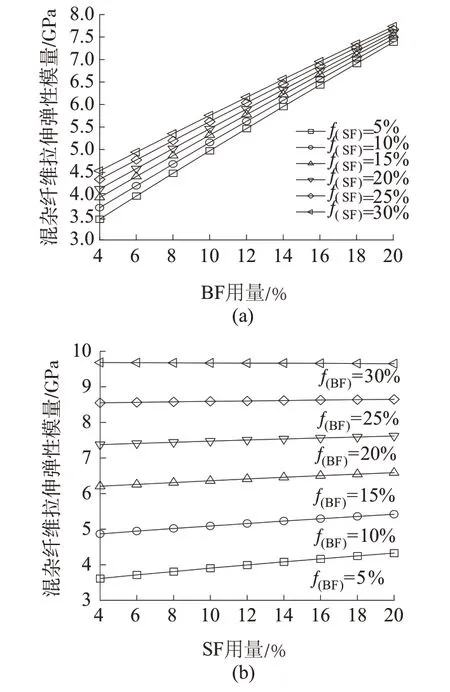
图8 混杂纤维增强PLA复合材料拉伸弹性模量随纤维用量的变化

3.2 混杂纤维拉伸弹性模量变化的影响分析

为了分析SF和BF拉伸弹性模量对混杂纤维增强复合材料拉伸弹性模量的影响,取SF拉伸弹性模量变化范围为10～22 GPa,BF拉伸弹性模量变化范围为80～92 GPa。运用笔者的细观力学计算模型对复合材料拉伸弹性模量进行预测,预测结果见图9a、图9b。图中E(SF)和E(BF)分别为SF,BF的固定拉伸弹性模量。从图9a、图9b中可以看出,在纤维含量保持不变的情况下,混杂纤维增强PLA复合材料的拉伸弹性模量随纤维拉伸弹性模量增大而线性增大。

图9 混杂纤维增强复合材料拉伸弹性模量随BF、SF拉伸弹性模量的变化

4 结论

基于等效夹杂原理和分步均匀化方法,提出了一种预测三相混杂复合材料纵向拉伸弹性模量的细观力学模型,并与已有的试验和有限元模拟结果对比,得出以下主要结论：

(1)基于等效夹杂理论可以有效预测两相复合材料的有效拉伸弹性模量,将其与分步均匀化方法结合,提出了能够预测三相混杂复合材料拉伸弹性模量的细观力学模型。

(2)运用细观力学模型计算了SF/BF混杂增强PLA复合材料的拉伸弹性模量,将模型计算结果与文献[15]试验结果进行对比,两者的最大相对误差基本保持在15%以内。与ABAQUS有限元模拟结果相比,模型计算结果更接近文献[15]试验结果,表明笔者提出的细观力学模型具有合理性。

(3)对于混杂复合材料只需确定基体与纤维的拉伸弹性模量,纤维体积分数及Eshelby张量,便可以用于计算植物纤维与人造纤维制成的三相混杂复合材料,为环保型复合材料的性能设计提供一定参考依据。