基于土力学原理的地下铲运机自主铲装过程力学特性分析
2022-10-26王振启杨支海赵晓燕
方 昊, 王振启, 杨支海, 赵晓燕, 严 勃
(1.北矿机电科技有限责任公司, 北京 100160; 2.紫金矿业集团股份有限公司, 福建 上杭 364200;3.云南驰宏锌锗股份有限公司 会泽冶炼分公司, 云南 会泽 654211)
地下铲运机的自主行驶与自主铲装技术是实现智能矿山中采矿过程全自动化的关键一步。如何高效稳定实现矿石料堆的自主铲装以及快速连贯完成矿石运输是目前制约矿山采矿效率的两个主要影响因素[1]。传统采矿装备工作效率低、自动化程度低、能耗大、污染重,这些因素成为地下采矿高效绿色发展的掣肘[2]。随着信息技术与计算机技术的飞速发展,矿山的自动化或智能化开采在全球范围内逐渐投入施行。如加拿大、芬兰与瑞典等国外传统采矿大国,为获取在采矿无人化中竞争的优先权,先后拟定了“智能化矿山”和“无人化矿山”的采矿发展规划,其最终目标是实现地下矿山生产全过程的无人化[3]。在地下矿山开采的工艺流程中,由于有轨车辆的灵活性差、爬坡能力低、配套设施建设成本高,使得采用有轨运输系统的地下矿山基建费用高昂。采用无轨矿用车辆代替有轨车辆已经成为国际地下矿山行业的发展趋势。提高车辆的使用效率和车辆的智能化控制水平是进一步提高矿山车辆运输效率的重要技术发展方向[4]。另一方面要实现“无人化”矿山,地下铲运机的自主铲装也是必须攻克的技术难点。目前地下铲运机已经初步实现了自主行驶和自主卸料的功能,但是自主铲装功能还没有实现。对于铲运机装- 运- 卸的三种工作属性而言,铲运机并没有达到智能化或者自动化。因此实现自主铲装,是铲运机自动化的必经之路,是解放生产力的必经之路[5]。本文以地下铲运机为研究对象,对自主铲装过程的力学特性进行了计算分析,为后续自主铲装控制算法设计和自主铲装运行提供理论参考和技术支持。
1 地下铲运机及铲装工作机构
地下铲运机整车结构由前车体、后车体、副车架与铲斗工作机构组成,其三维结构如图1所示。

图1 地下铲运机基本结构
铲运机经过多年技术研发,其铲装工作机构主要包括正转四连杆工作机构、正转五连杆工作机构、正转六连杆工作机构和反转六连杆工作机构[6-7]。地下铲运机工作装置主要由举升油缸、转斗油缸、动臂、铲斗、摇臂、连杆以及前车架7个组件构成。整个工作装置连接在铲运机前机架上,铲斗通过动臂、举升油缸连接,实现铲斗的举升和回落功能;通过连杆、摇臂与转斗油缸连接,实现铲斗的翻转和回收功能[8]。地下铲运机铲装工作机构如图2所示。

图2 铲运机铲装工作机构
2 铲装过程分析
铲运机的铲装工作过程通常可以分为四个阶段:
(1)空载行驶阶段
铲运机在卸料后,铲斗回落、后退并转向,然后向矿房料堆方向快速行驶,在离料堆一定距离时,完成料堆扫描识别,获取铲装指令,切换成低速档并放下铲斗;
(2)铲装阶段
铲运机以全力铲入矿石料堆,并操纵铲斗动臂油缸和转斗油缸,控制铲斗铲装,直至铲斗装满;
(3)满载运行阶段
铲运机铲装完毕后,车辆后退一定距离后落斗并转向,然后向溜井或者矿用卡车方向前进;
(4)卸料阶段
铲运机动臂举升到卸料位置,使铲斗前翻卸料。
从铲运机的铲装过程可以发现,铲运机的作业方式是在铲运机行驶过程中配合以工作装置的动作进行的。当铲运机处于不同的工作状态时,动力消耗变化较大,如表1所示。

表1 铲装过程动力消耗情况表
由表1可见,地下铲运机能耗最大的阶段是铲装阶段。由此铲装阶段的自动化也需要考虑铲装的效率与能耗。提高铲装效率,一般有缩短铲装时间和增加单次铲装质量两种途径。对于给定铲运机,只能通过缩短铲装时间来实现铲装效率的提高。即在保证满斗率的情况下,用最短时间完成铲装作业。
为确保自主铲装操作的连贯性,铲装轨迹曲线应连续且光滑。结合铲装工作过程,设计铲装轨迹曲线如图3所示。

图3 铲装轨迹曲线
3 铲装过程力学特性分析
在实际工作中,铲装阻力很难直接测量得到,因此,本文通过模拟计算,提出一种铲装阻力的估算方法。在铲装过程中,假定铲装阻力和铲运机的牵引力动态平衡,利用牵引力来估算铲装过程的铲装阻力。
3.1 铲装阻力的理论计算
铲装阻力按铲装阶段划分可以分为插入阻力和铲取阻力。插入阻力是铲斗随着铲运机的推进,铲入矿石料堆的过程中受到的反作用力。铲取阻力是铲斗铲入矿石料堆一定深度后,随着两工作油缸的提升或者翻转动作,料堆对铲斗的反作用力。
对铲装阻力的计算的研究,开始于二十世纪八十年代,历经了苏联学者从实验中提炼的经验公式,近代学者利用散体理论和土力学原理对铲装阻力进行计算。但是这些理论分析方法都是针对松散细颗粒料堆的计算,对于大块度的料堆,这些计算要么误差很大,要么不适用。随着计算机技术的发展,依据有限元法和离散元法发展出了铲装阻力的数值模拟计算方法,通过模拟料堆颗粒,设定颗粒属性,形成料堆,再导入铲斗模型和运动轨迹,完成铲装过程中的铲装阻力的仿真。这种方法不仅应用在松散颗粒料堆,还可以应用在大块度料堆,比如爆破矿石。
(1) 基于苏联经验公式对铲装阻力计算[9]
插入阻力的计算公式如式(1)所示:
(1)
式中PBH—总的水平插入阻力;
K1—物料粒度的影响系数;
K2—物料种类的影响系数;
LBH—铲斗铲入料堆的深度;
B—铲斗宽度;
K3—料堆高度影响系数。
铲取阻力主要为剪切阻力,一般而言,开始提升时刻出现最大铲取阻力,随着铲斗的提升翻转,逐渐远离料堆,铲取阻力逐渐减小。初始铲取阻力可用如公式(2)计算:
PW=2.2LBHBKc
(2)
式中PW—铲斗铲取阻力;
LBH—铲斗铲入料堆的深度;
B—铲斗宽度;
Kc—物料的剪切阻力。
基于实验的苏联经验公式在进行理论计算时,其最大的不足表现为需要选取的系数比较多。系数多,计算时人为误差比较大。此外,很多系数需要实际测量得到,而且因为系数过多,铲装阻力与系数的关系在铲装过程中难以明确的表征。
(2) 基于土力学原理的铲装阻力计算
铲取阶段的受力比较复杂,受力如图4 所示。P1是矿石物料的重力,作用点在铲斗内矿石的质心。P2是矿石料堆阻力,由铲运机的推进挤压产生。P3是铲斗壁和矿石料堆的摩擦力,与运动方向相反。P4是铲斗提升或翻转引起的铲取阻力,作用于铲取边缘上。P5是铲斗与矿石料堆运动产生的惯性力[10]。

图4 铲取阻力受力模型
料堆轮廓曲线函数C:y-f(x)=0,铲斗斗刃运行轨迹曲线函数Cd:y-fd(x)=0。点P为铲斗斗刃,点Q为斗底。下面对铲取阻力的各分力进行计算。
P1是铲装矿石物料的重力,这里根据铲装轨迹计算铲装过程中矿石的体积,然后结合矿石料堆的密度,计算物料的重力。
(3)
式中α—矿石的体积修正系数;
γ—矿石料堆的重度;
B—铲斗宽度;
XS—点S的X轴坐标。
P2是料堆对铲斗斗底的阻力,这个阻力在铲斗斗底没有和料堆接触时为零。本文中假定斗刃轨迹满足铲斗斗底与料堆产生接触的条件,并忽略个别矿石棱角对铲斗斗底的刮蹭。
P3是铲斗侧壁与矿石料堆之间的摩擦力,这里的正压力不仅由铲斗内的矿石产生,还由铲斗上方的矿石料堆产生。本文的铲装过程,因铲斗没有彻底的铲入矿石料堆,所以铲斗侧壁的摩擦力不考虑铲斗其他部位的摩擦力。
(4)
式中μ—矿石的摩擦系数。
P4是斗刃与矿石料堆因挤压形成得铲取阻力,在铲装过程中,矿石在这个力的作用下与料堆分离,掉落在铲斗中;因在铲装过程中随机性很大,这个力的计算对铲装过程的研究作用不大,这里用剪切阻力来代替。
P4=2.2(XP-XS)BKc
(5)
P5是由于矿石在铲装过程中的惯性力,这个力在铲斗与料堆发生显著地加速运动时比较明显,因为铲装过程是一个负载不断增加地过程,铲运机在这个过程中常常使用低速档,缓慢稳定地铲装,本文的计算将P5设定为零。
经过上述分析计算,利用如下公式,可以将各分力合成为铲取阻力水平分力和垂直分力。
(6)
3.2 铲装阻力的估算方法
根据铲装过程中铲运机牵引力和铲装阻力水平分量的动态平衡。考虑到铲装阻力并不是一个水平力,它的垂直分量会对车辆的支撑力产生影响,这里对文中的道路阻力进行修正。得到如下公式
Fq=F-Fψ=F-(G+Py)(f+i)=Px
(7)
式中G—铲运机在铲装时的重力,N;
Fq—铲运机的牵引力,N。
对上述公式进行变换可以得到
Px+Py(f+i)=F-G(f+i)
(8)
于是需要找到一个方法对Py进行计算,即对铲装阻力的垂直分力进行计算。本文提出两种方法进行估算,第一种是根据铲运机工作装置的工作油缸的油压计算铲斗的铲取力,认为铲取力的垂直分量和铲装阻力的垂直分量相等。这种方法的缺陷是忽略铲装过程中的铲斗运动加速度。第二种方法是通过经验,总结铲装过程中铲装阻力水平分量和垂直分量的一般性数值关系,利用铲装阻力的水平分量代替垂直分量。
这里利用铲运机工作装置的动力学分析结果计算得到铲斗的驱动力Fp,这个力的垂直分力与铲装阻力垂直分力达到平衡,由此可以得到Py,这样可以结合铲运机的牵引力计算得到铲运机在铲装过程中的铲装阻力的水平分力。图4是由仿真模型得到的铲运机工作装置的铲取力。
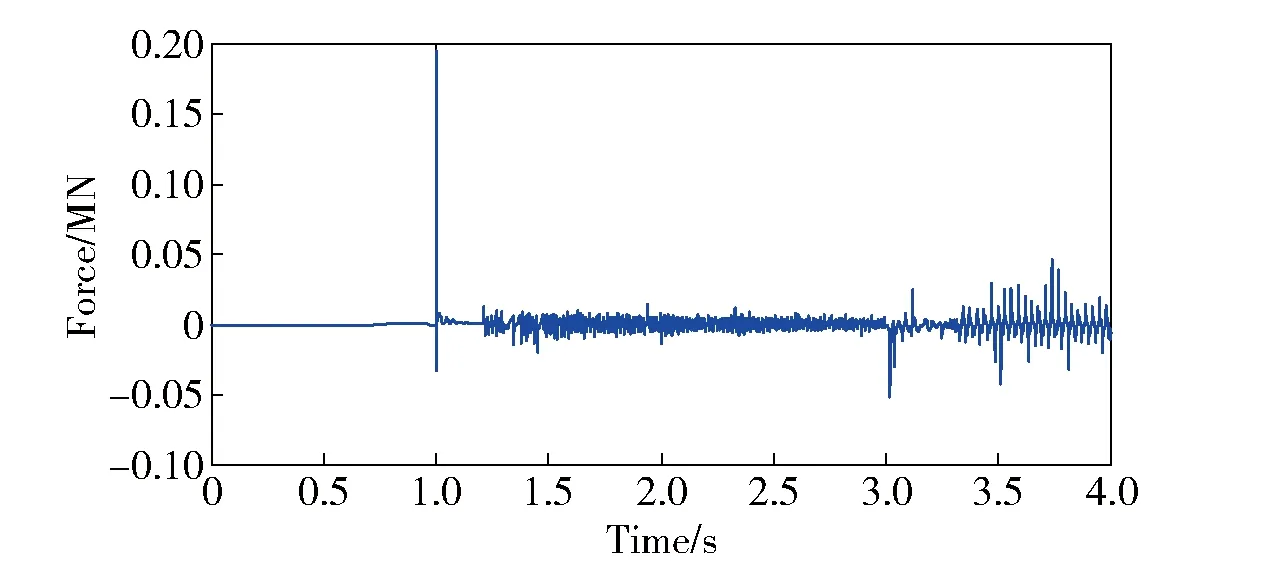
图5 铲装过程铲斗斗刃的铲取力

图6 剔除突变点后的斗刃的铲取力
从图5中可以看到在无负载工况下,铲装插入阶段与铲取阶段的分界点,铲取力产生突变激增到200 kN。这时的工况是铲斗由平放状态进行翻转和举升状态。这个铲取力的激增,可能是由于铲斗加速度方向的突变产生的。这里除去突变点的数据后,铲取力的垂直分力如下图6所示。从图6中可以看出无负载工况下,铲取力垂直分量一般在10~20 kN,在实际铲装时铲取力会依据铲装阻力产生变化。
第二种方法是依据铲装过程中的铲装阻力的垂直分量和水平分量的统计学关系,总结出铲装阻力的垂直分量和水平分量的大致比例关系,αPx=Py,于是可得:
(9)
在铲运机工作时,可根据上述公式进行估算铲装阻力。
4 结论
(1)分析了地下铲运机及铲装工作机构组成及工作原理;
(2)对铲装过程进行分析,获得了连续且光滑的铲装轨迹曲线;
(3)提出了一种铲装阻力的估算方法,基于土力学原理,建立了铲取阻力受力模型,在铲装过程中,假定铲装阻力和铲运机的牵引力动态平衡,利用牵引力来估算铲装过程的铲装阻力。
(4)为后续自主铲装控制算法设计和自主铲装运行提供理论参考和技术支持,具有重要的工程应用价值。
