由一个平抛运动的错误解答引发的思考
2022-10-26曹芳
曹 芳
(广东惠州市东江高级中学)
平抛运动是高中物理学中最重要的物理模型之一,在近5年的全国卷和单独命题的省份试卷中每年都会有涉及.本文以飞机投弹这一经典模型为例,从一道经典例题的错误解答入手,分析错误的根源,利用平抛运动的基本特点,通过两种特殊方法,寻找求解飞机投弹类问题的钥匙,以期达到触类旁通的目的.
例如图1 所示,战斗机沿水平方向匀速飞行,先后释放三颗炸弹,分别击中山坡上等间距的A、B、C三点,已知 击中A、B的时间间隔为t1,击中B、C的时间间隔为t2,不计空气阻力,则().

图1
A.t1<t2B.t1=t2
C.t1>t2D.无法确定
错误解析高中物理多种教辅资料中均有本题,答案多数选的是A,分析过程如下:如图2 所示,A、B、C三点等间距,由几何关系可知,AA1、BB1的竖直高度差相同.设1、2两炸弹在空中运行的时间差为Δt1,2、3两炸弹在空中运行的时间差为Δt2,则Δt1为炸弹1从A1到A的时间,Δt2为炸弹2从B1到B的时间,由于平抛运动在竖直方向上做自由落体运动,越往下竖直分速度越大,故Δt1<Δt2,从而得到t1<t2,故选项A 正确.
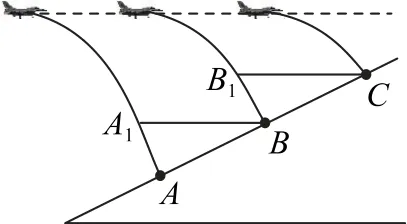
图2
此解法错误的原因是把炸弹在空中运行的时间差和落地的时间间隔等同了,只有三颗炸弹同时投出,才能得到这一结论.实际上这三颗炸弹是从同一架战斗机上先后投出的,炸弹落地的时间间隔由投弹时间间隔和炸弹在空中运行的时间差共同决定.设三颗炸弹投弹的时间间隔分别为t12和t23,则t1=t12-Δt1,t2=t23-Δt2,本题t12和t23的大小关系不明确,故无法直接由Δt1<Δt2得到t1<t2.对于t1=t12-Δt1关系式,可这样类比:1、2两位同学先后从教室出发去食堂吃饭,出发的时间间隔t12为5分钟,但是在去往食堂的路上1同学走得比较慢,比2同学多花的时间Δt1为1分钟,两位同学到达食堂的时间间隔t1就应该等于t12-Δt1,为4分钟.

图3
拓展1试比较三颗炸弹投弹的时间间隔t12和t23的大小关系.
分析由前面的分析可知t1=t12-Δt1,t2=t23-Δt2,因t1=t2,Δt1<Δt2,故t12<t23,即只有逐渐增大投弹的时间间隔,在山坡上击中的A、B、C三点才能等间距.
拓展2若飞机顺坡投弹,三颗炸弹分别击中图4 中山坡上等间距的A、B、C三点,击中A、B和B、C的时间间隔分别为t1、t2,三颗炸弹投弹的时间间隔分别为t12和t23,试比较t1和t2、t12和t23的大小关系.

图4
分析三颗炸弹分别击中山坡上的A、B、C三点时,战斗机分别位于A、B、C三点的正上方,因AB=BC,故t1=t2.设1、2两炸弹在空中运行的时间差为Δt1,2、3两炸弹在空中运行的时间差为Δt2,由前面分析可知Δt1>Δt2,因炸弹1先投且在空中运行的时间更 短,故t1=t12+Δt1,同理有t2=t23+Δt2,故t12<t23,即只有逐渐增大投弹的时间间隔,在山坡上击中的A、B、C三点才能等间距.
小结不管飞机是迎坡投弹还是顺坡投弹,若要击中山坡上等间距的点,投弹时间间隔都要逐渐增大,而炸弹落地的时间间隔总是相同的.
变式1如图5 所示,一架战斗机沿水平方向匀速飞行,等时间间隔先后释放三颗炸弹,分别击中山坡上的A、B、C三点,则三个击中点的间距关系为().
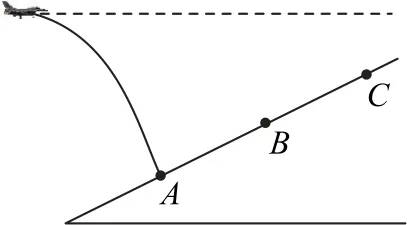
图5
A.AB>BCB.AB<BC
C.AB=BCD.无法确定
常规赛后半段已经在紧锣密鼓地进行,西王2019年的“后”希望,也在于需要大纪和大龙动员一切可能的力量,绝境反击,在强敌环绕中杀出一条血路来,毕竟,两军相遇勇者胜,大纪和大龙都是身经百战的老江湖了,他们懂得,上赛季总决赛四强的队伍,不应该人见人欺,倘不能扭转这一窘境,那大纪和大龙,也就尴尬了。
解法1(几何法) 因战斗机沿水平方向匀速飞行,故三颗炸弹在空中运动的轨迹完全相同,如图6所示,作出三颗炸弹在空中的运动轨迹,过B点作水平线与另外两条抛物线分别相交于A1、C1,过A1、C1分别作两抛物线的切线,切线与山坡的交点分别为D、E,故A1D∥C1E,因三颗炸弹是等时间间隔先后释放的,故A1B=BC1,从而△A1DB≌△C1EB,故DB=EB,AB>BC,答案选A.
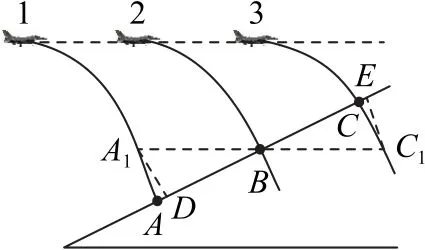
图6
解法2(假设法) 假设AB=BC,由前面分析可知,投弹时间间隔为t12<t23,根据已知条件t12=t23,炸弹2相比AB=BC情况应延迟一点投出,则炸弹2落点必定落在BC之间,故答案是AB>BC.
拓展设炸弹击中A、B的时间间隔为t1,击中B、C的时间间隔为t2,试比较t1和t2的大小关系.
分析如图3所示,三颗炸弹分别击中山坡上的A、B、C三点时,战斗 机分别 位于A、B、C三点的正上方,因AB>BC,故水平位移x12>x23,因战斗机沿水平方向匀速飞行,故t1>t2.
小结从同一战斗机上等时间间隔先后释放的三颗炸弹,落在山坡上的时间间隔会逐渐减小,弹坑的间距也逐渐减小,此结论同样适用于逆坡投弹.
变式2如图7所示,甲、乙、丙三架战斗机排成一列纵队,且相邻两架飞机间距相同,它们沿水平面以相同速度匀速飞行,某时刻它们同时释放一颗炸弹,分别击中山坡上的A、B、C三点,则三个击中点的间距关系为().
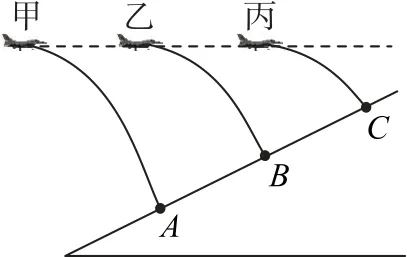
图7
A.AB>BCB.AB<BC
C.AB=BCD.无法确定
解法1(几何法) 因三架战斗机飞行速度相同,故三颗炸弹在空中的运行轨迹也完全相同,变式1的解法1同样适用于本题,不再复述.
解法2(假设法) 三颗炸弹下落的高度不同,在空中运行的时间也不同,且有t丙<t乙<t甲,如图8所示,当乙炸弹击中B点时,乙战斗机恰好位于B点的正上方B1点,此时甲炸弹还未到达A点,故甲战斗机在A1后方,设甲战斗机离A1的距离为s1,丙战斗机已经飞离了C1,设丙战斗机此时离C1的距离为s2.假设AB=BC,则有A1B1=B1C1,DA=EB .设甲、乙两炸弹在空中运行的时间差为Δt1,乙、丙两炸弹在空中运行的时间差为Δt2,根据自由落体运动的特点可知Δt1<Δt2.设三架战斗机水平飞行的速度为v,则s1=vΔt1,s2=vΔt2,很显然s1<s2,即只有s甲乙<s乙丙时,才有AB=BC.若要满足假设,在三架战斗机等间距排列情况下,应该让乙战斗机的位置往前靠一些,则乙投出的炸弹落点必定落在BC之间,故AB>BC.

图8
小结无论是一架飞机等时间间隔先后投弹,还是三架等间距飞机同时投弹,在斜坡上留下的弹坑间距都是逐渐减小的.值得注意的是,若三颗炸弹是先后投放的,击中目标的时间间隔不止与炸弹在空中运行的时间差有关,还跟投弹的时间间隔有关;若三颗炸弹是同时投出的,则击中目标的时间间隔仅与三颗炸弹在空中运行的时间差有关.
综上所述,解决飞机投弹类问题的关键是三点:1)抓住炸弹在竖直方向做自由落体运动的运动特点,找出炸弹在空中运行的时间关系;2)抓住其水平方向做匀速直线运动的特点,找到飞机和炸弹的位置关系;3)找准炸弹落地时间间隔和投弹时间间隔、炸弹在空中运行的时间差的关系.抓住了以上三点,此类问题便能迎刃而解.
(完)
