椭圆轨道类天体运动问题的突破方法
2022-10-26刘晓花
刘晓花
(山东省平度市第九中学)
椭圆轨道类天体运动问题,因其运动轨迹的特殊性,分析的方法与圆周类天体运动问题有所不同,近几年的全国高考卷和地方高考卷对该类问题都有所涉及,如2021年高考全国乙卷第18题和福建卷的第8题均对此进行了考查,其中福建卷还涉及了椭圆的偏心率.试题难度不大,但考后统计表明,学生对该类问题的作答却不尽人意.究其原因主要有三点:一是学生对椭圆知识不熟悉,应用数学工具分析物理问题的意识淡薄;二是对万有引力定律和向心力公式中的“r”认识模糊,将二者中的“r”混为一谈;三是受思维定式的影响,在椭圆运动中盲目套用天体圆周运动的规律.那么如何有效突破这一问题难点呢? 笔者认为要着重把握好以下两个方面.
1 熟悉椭圆知识,树立数理意识
1.1 长轴、短轴和焦距
在如图1所示的椭圆中,左、右两端点A、B之间为长轴,记为2a,上、下两端点C、D间的距离为短轴,记为2b,两焦点F1、F2之间的距离为焦距,记为2c,三者之间的关系为(2a)2=(2b)2+(2c)2,即有a2=b2+c2.
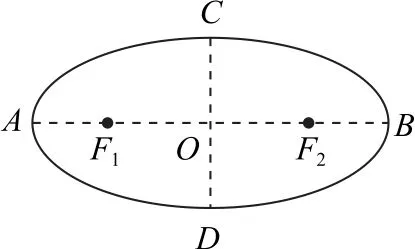
图1
1.2 离心率和曲率半径
1)离心率:是椭圆扁平程度的一种量度,离心率定义为椭圆焦距和长轴的比值,用e表示,即e=.
2)曲率半径:曲率半径主要是用来描述曲线上某处曲线弯曲变化的程度,在椭圆中,A、B两端点处的曲率半径定义为椭圆半短轴的二次方和半长轴的比值,用ρ表示,即ρ=
2 厘清两个关系,把握问题本质
1)椭圆轨道中,近点和远点的速度关系
如图2所示,一天体m绕另一天体M运动,其运动轨迹为椭圆,天体M处在椭圆其中一个焦点上,可认为静止不动.设OA间的距离为rA,OB间的距离为rB,天体m运动到A点和B点的速度大小分别为vA和vB.
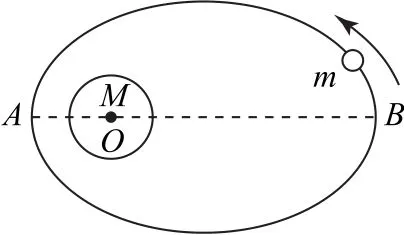
图2

2)不同中心天体的质量关系
由开普勒第三定律可知,所有行星轨道的半长轴的三次方跟它的公转周期的二次方的比都相等,即有,这个规律对其他天体系的椭圆运动和圆周运动同样适用.但公式中的k与中心天体的质量存在着怎样的关系,及不同中心天体的质量如何建立联系,大部分学生并不清楚,这也是导致2021年高考全国乙卷第18题和福建卷的第8题得分率较低的一个主要原因.下面,我们以天体圆周运动为例进行推导.
如图3所示,天体m绕中心天体M做匀速圆周运动,则由万有引力提供向心力有,故有
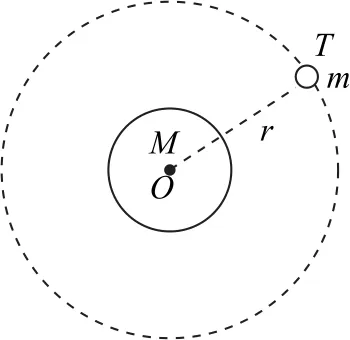
图3
由此,再反观开普勒第三定律便不难得出,无论绕“中心”天体做椭圆运动还是圆周运动,均有k=.可见,k与中心天体的质量成正比,不同中心天体的质量则可通过对应的椭圆半长轴(或圆周半径)和公转周期建立联系.
例(2021年福建卷)两位科学家因为在银河系中心发现了一个超大质量的致密天体而获得了2020年诺贝尔物理学奖.他们对一颗靠近银河系中心的恒星S2的位置变化进行了持续观测,记录到的S2的椭圆轨道如图4所示.图4 中O为椭圆的一个焦点,椭圆偏心率(离心率)约为0.87.P、Q分别为轨道的远心点和近心点,Q与O的距离约为120AU(太阳到地球的距离为1AU),S2的运行周期约为16年.假设S2的运动轨迹主要受银河系中心致密天体的万有引力影响,根据上述数据及日常的天文知识,可以推出().
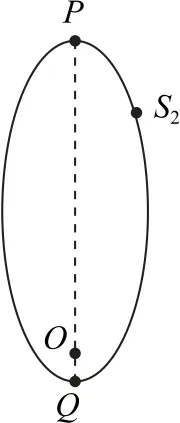
图4
A.S2与银河系中心致密天体的质量之比
B.银河系中心致密天体与太阳的质量之比
C.S2在P点与Q点的速度大小之比
D.S2在P点与Q点的加速度大小之比


总之,分析椭圆轨道类天体运动问题时,要以“椭圆”为切入点,强化数学方法分析物理问题思维,以开普勒第三定律为纽带,建立天体椭圆运动与圆周运动的关联,明确近点和远点所遵循的运动规律,辨析中“r”在不同情境中表示的不同含义,只有这样,才能以不变应万变,灵活分析问题和解决问题.
链接练习
航天飞机在完成对哈勃空间望远镜的维修任务后,在A点从圆形轨道Ⅰ进入椭圆轨道Ⅱ,B为轨道Ⅱ上的一点,如图5所示,关于航天飞机的运动,下列说法正确的有().

图5
A.在轨道Ⅱ上经过A的速度等于经过B的速度
B.在轨道Ⅱ上运动的周期大于在轨道Ⅰ上运动的周期
C.在轨道Ⅱ上经过A的速度小于在轨道Ⅰ上经过A的速度
D.在轨道Ⅱ上经过A的加速度小于在轨道Ⅰ上经过A的加速度
链接练习参考答案
C.
(完)
