基于有限元及贝叶斯网络的数控滚齿机热误差建模研究

樊隆祥，周启武，彭东林，郑 永，徐 是

(重庆理工大学 机械检测技术与装备教育部工程中心， 重庆 400054)

0 引言

机床热误差占已知加工误差的40%～70%[1]，严重影响机床加工精度。对于数控滚齿机，热误差是一个主要误差源[2]，有必要建立有效的补偿方式。建立一个准确的数控滚齿机热误差模型是一个重要环节，好的建模结果使得补偿更为有效，更利于提升滚齿加工精度。

就数控机床热误差模型而言，李彬等[3]利用遗传算法自适应的全局优化搜索特性和小波神经网络的时频局部特性建立了数控机床的热误差补偿模型，提高了热误差补偿的精度及效率；Liu等[4]提出一种改进的灰狼优化算法(IGWO)和广义回归神经网络相结合(GRNN)的滚齿机热误差模型，将模糊聚类和平均影响值相结合，从而减少温度变量间的耦合。本文以改造的数控滚齿机作为对象，进行热-结构仿真分析，基于仿真数据，选择多个对机床主轴热误差影响大的部件的温度数据，对温度变量进行模糊聚类分析，然后通过与主轴热位移相关性比较筛选得到滚齿机热误差建模的热关键点，同时减少了温度传感器数量，最后基于贝叶斯网络建立数控滚齿机热误差的数学模型。

1 数控滚齿机模型

该数控滚齿机主要由立柱、直驱滚刀轴系统、工作台、进给系统、床身等组成，其结构如图1所示。三维模型主要为刀架部分模型，对其余结构做了简化，如图2所示。

图1 滚齿机组成 图2 滚齿机三维模型

2 数控滚齿机热源和边界条件分析

2.1 数控滚齿机热源分析计算

数控滚齿机床热源主要来自滚刀切削热、电机发热及轴承的发热[5]。

2.1.1切削热

切削过程中，切削热大部分由切屑带走，取5%的切削热量传至滚刀[6]，切削热的计算公式：

Q=Pν

(1)

式中：Q为热功率;P为切削力;ν为主轴转速。

滚刀最大力矩计算[7]：

(2)

P=2Mmax/d

(3)

式中：m为法向模数；S为轴向进给量；T为吃刀深度；ν0为主轴转速；z为齿轮齿数；K材为齿轮材料修正系数，根据加工材料选取相应的系数；K硬为工件硬度修正系数；K螺为螺旋角修正系数；d为滚刀外径。

2.1.2轴承热

轴承的摩擦发热是滚齿机的一个主要热源，本结构中滑动轴承是主要热源，其摩擦热计算为[8]

Q1=fpv

(4)

式中：Q1为摩擦升热；f为摩擦因数；p为轴承载荷；v为轴颈圆周速度。

该数控滚齿机机床中滚动轴承为推力球轴承，其发热功率计算[9]：

q=1.047×10-4M·n

(5)

M=M0+M1

(6)

式中：q为功率；M为轴承摩擦力矩；n为主轴转速；M0为载荷摩擦力矩；M1为粘性摩擦力矩。

(7)

M1=f1p1dm

(8)

式中：f0为轴承型号与润滑方式的相关常数；f1为轴承型号和负载的相关常数；ν为润滑剂运动黏度；p1为轴承摩擦的力矩计算载荷；dm为轴承中径。

2.1.3主轴直驱电机发热

主轴电机的发热主要为定子铜耗和铁芯损耗，其发热表示为[10]：

Qd=P1(1-η)

(9)

式中：Qd为电机生热；P1为电机输入功率；η为电机效率。

2.2 边界条件分析计算

滚齿加工中，刀架主轴、电机转子转动与空气及滚刀的切削液冷却均为强迫对流换热。强迫对流换热系数公式[6]：

(10)

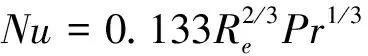
(11)

(12)

式中：α为对流换热系数；Nu、Re、Pr为努塞尔特数、雷诺数、普朗特数；λ为流体导热系数；ds为主轴当量直径；ω为主轴角速度；νf为流体运动黏度。

电机水冷为管内强迫对流，对流换热公式[11]：

(13)

(14)

式中：h1为换热系数；D为几何特征定型尺寸；u为流体特征速度；ν为水的运动黏度。

3 数控滚齿机热-结构仿真

采用以下参数作为仿真条件，分析滚齿机受热与变形。齿轮参数：m=6，z=20，β=10°，材料为45钢；滚刀参数：d=105 mm，z1=1，轴向进给量S=2 mm/r，n=160 r/min，吃刀深度T=1 mm。用于机床仿真的主要材料参数如表1所示，表2为根据加工条件进行的热源强度值。

表1 机床仿真主要零件材料参数

表2 机床热源强度

环境温度设定为20 ℃，分析热边界条件，表3为刀架部分的强迫对流换热系数。

表3 机床换热系数

利用有限元计算软件完成稳态热-结构仿真。图3为模型的四面体网格划分和三维坐标的标识，研究主要围绕机床刀架主轴热误差展开，因此对主轴部分做了网格细化，主轴细化程度对主轴热变形计算结果无明显差别，模型的单元数为397 046，节点数为632 875。

以计算出的热功率和对流系数作为热分析条件进行稳态热仿真，得到如图4所示的机床达到热平衡状态时的温度分布图。结果显示，水冷虽然带走了电机定子大部分的热量，但仍有一部分滞留在电机内部，电机转子温升明显，温度达到41.6 ℃；滑动轴承部分的温度上升也较多，尾座轴承达到33 ℃；滚刀冷却效果较好，温度变化较小。

以稳态热分析结果作为结构仿真分析的条件，并设置机床底座的底面为固定约束，得到图5—8所示的机床热位移分布情况，其结果的趋势与温度分布趋势相当，靠近轴承和电机内部的区域因温度较高导致热位移较大，最大的变形发生在电机转子部位，约92 μm；滚刀主轴部分的变形较小，约35 μm，同时图6—8的结果显示滚刀主轴部分主要表现为X和Y2个方向的热位移，Z方向则相对较小。

图3 网格划分 图4 稳态温度场

图5 稳态热位移 图6 X向热位移

图7 Y向热位移 图8 Z向热位移

为得到机床温升和主轴热位移变化情况，进行滚齿机瞬态热-结构仿真，提取机床热源附近7个重要部件温度(分别为T1-T7，其中滑动轴承Ⅱ位于主轴中部)和滚刀主轴热位移的数据如图9、图10所示。随时间推移，滚齿机各部分温度持续上升，滚刀主轴热位移也随温度的上升而增大，与稳态仿真结果分析一样，主轴的热位移主要为X和Y2个方向。

图9 滚齿机各部分温升曲线

图10 滚刀主轴热位移曲线

4 贝叶斯网络的滚齿机热误差建模

4.1 基于模糊聚类的温度优化

机床热-结构的仿真数据一定程度上反映了机床的误差情况，因此提取瞬态仿真的重要温度变量数据来进行温度优化，从而获得机床热关键点，方法采用模糊聚类[12]，首先构建模糊等价矩阵，计算各温度变量间的相似系数rij组合成n阶相似系数矩阵(rij)n×n，记为R。相似系数rij采用皮尔逊相关系数计算方式。相关系数rxy公式[13]：

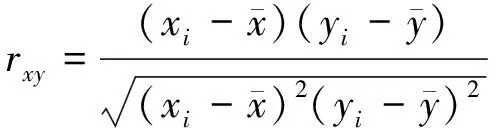
(15)

式中：x、y为变量。

采用数学平方法求出相似系数矩阵R的传递闭包R，运算如下：

R→R2→R4→…

(16)

表4所示为温度变量分类情况及与热位移相关系数大小。依据温度变量Ti与热位移E的相关性系数大小得到机床热关键点，同时电机主轴的相关性相对较小，因此以滚齿机刀架、刀架尾座轴承、滑动轴承Ⅱ作为滚齿机热误差建模的热关键点。

表4 温度变量分类

4.2 基于贝叶斯网络的滚齿机热误差的构造理论

贝叶斯网络是一种模拟人在推理过程中对于因果关系的不确定性的处理模型。一组变量X={X1,X2,…,Xn}的贝叶斯网络包含由组中所有变量节点共同组成的网络S，如图11所示。

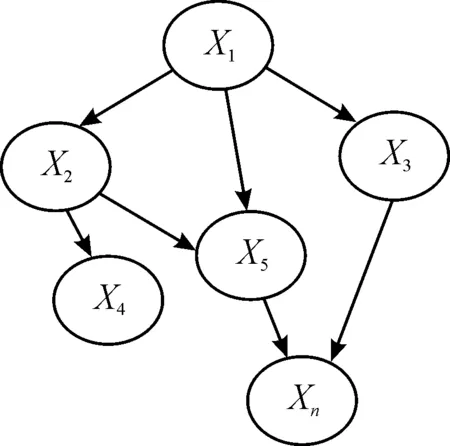
图11 网络结构S

网络结构S是由各个节点之间共同构成的有向无环图，节点之间采用单箭头进行连接则表示2个节点变量之间的依赖关系，箭头一端为“因”，一端为“果”，节点间的不确定性通过概率P量化表示[14]。简言之，把某个研究系统中涉及的随机变量，根据是否条件独立绘制在一个有向图中，就形成了贝叶斯网络。

图11中节点X1影响到节点X2，用从X1指向X2的箭头建立有向弧(X1，X1)，权值用条件概率P(X2|X1)表示，同时，对于随机变量X的联合概率分布由各自的局部条件概率分布相乘得到：

(17)

贝叶斯网络的热误差建模过程主要分为3步：贝叶斯网络先验网络构造、样本数据的网络学习以及贝叶斯网络推理的热误差预测，如图12所示[15]。

图12 贝叶斯网络的机床热误差建模过程

根据贝叶斯网络，由刀架尾座轴承、刀架、滑动轴承Ⅱ作为热关键点与滚刀主轴热误差一起构成网络的节点集合，为简化网络和降低建模的难度，假设温度节点间是相互独立的，构造的3个温度点下的贝叶斯网络结构如图13所示。

图13 3个温度点下的贝叶斯网络

4.3 机床热误差实验及误差预测模型

实验采集机床热关键点的温升和滚刀主轴热误差的数据，以滚刀主轴X方向的热误差作为实验对象进行空载实验，实验装置如图14所示。滚刀主轴转速160 r/min，环境温度20 ℃，温度测量采用DS18B20温度传感器。

根据4.2节贝叶斯网络的理论建立热误差模型。首先对实验数据变量域进行确定，数据的特征统计如表5所示，以尾座滑动轴承温度T1和热误差E为例。ΔT1为各温度变量T1相邻采样点的差值(单位：℃)，ΔE为热误差数据E相邻采样点的差值(单位：μm)。

图14 数控滚齿机温度及热误差采集实验装置

表5 数据特征统计

根据表5，将ΔT1和ΔE的值域均匀的划为10个区间，每个区间对应于一个状态域，完成数据的离散化，如表6所示。

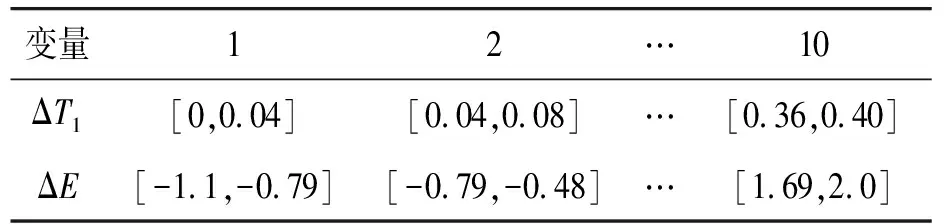
表6 变量状态域划分

确定变量对应的变量域后，得出ΔT1和ΔE独立分布概率(整个数据中该变量落在不同状态域的概率)，如表7所示。

表7 变量的独立分布概率

得出ΔT1和ΔE之间的条件概率P(ΔT1|ΔE)，如表8所示。

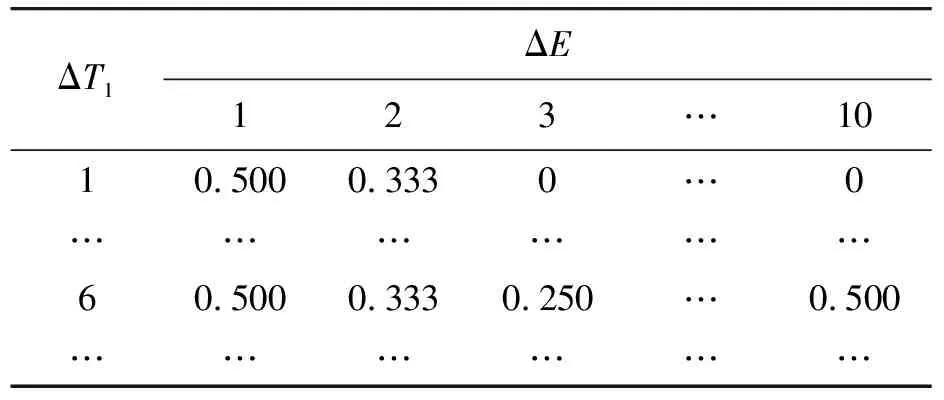
表8 条件概率

计算max{Pk(ΔEj|ΔT1m,ΔT4n,ΔT5p)}，即变量ΔTi(i=1,4,5)的状态域确定的条件下，变量ΔEj最大概率处于1～10的某个状态域(k为变量数据组号；j,m,n,p为状态域编号)，取此时j所对应的误差变量的状态域作为本组ΔEk的预测区间，取状态域的中值作为ΔEk的预测值，得出：

Ek+1=Ek+ΔEk

(18)

式中：Ek+1为第k+1组的热误差预测值；ΔEk为第k+1组和第k组热误差差值的预测值。

建立贝叶斯网络热误差预测模型后，导入实验数据进行热误差结果预测。数控滚齿机热关键点温度数据如图15所示，根据贝叶斯网络建立的滚齿机热误差模型，其热误差实验数据与预测模型的结果比较如图16所示。热误差预测模型的变化趋势与实际热误差的变化趋势较为一致，同时在7 h内二者残差最大为3.5 μm，预测结果较为准确。

图15 滚齿机及热关键点温度曲线

图16 滚齿机热误差实验数据与贝叶斯网络预测值曲线

5 结论

1) 基于传热理论完成了数控滚齿机整机的热特性分析，明确了机床的主要热源，进行机床热-结构仿真，分析了机床温度及热位移情况。

2) 采用模糊聚类对温度变量的优化，消除了温度变量间的耦合，使关键温度测点从7个减小为3个，减少了实验所需的传感器，降低了建模的难度。

3) 采用贝叶斯网络建立的数控滚齿机热误差模型对热误差进行预测，并把模型预测误差数据与实测误差数据进行比较，残差最大为3.5 μm，表明所提热误差模型是有效的，预测精度较高。