阵元失效下基于矩阵重构的MIMO雷达DOA估计
2022-10-26陈金立李家强
陈金立, 张 程, 陈 宣, 李家强
(1. 南京信息工程大学气象灾害预报预警与评估协同创新中心, 江苏南京 210044;2. 南京信息工程大学电子与信息工程学院, 江苏南京 210044;3. 南京信息工程大学物理与光电工程学院, 江苏南京 210044)
0 引言
多输入多输出(Multiple-Input Multiple-Output,MIMO)技术给雷达系统性能带来了全新的突破。与传统雷达相比,MIMO雷达在目标分辨与参数估计、低截获以及杂波抑制等方面有潜在的优势。波达方向角(Direction of Arrival,DOA)估计是MIMO雷达目标参数估计中的重要组成部分,主要有子空间类和稀疏表征类等DOA估计方法。在实际应用中,由于元器件长时间使用老化和恶劣环境的影响会导致天线阵元物理性损坏。由于失效阵元无法正常发射和接收信号,因此MIMO雷达经匹配滤波处理后所形成虚拟阵列中存在大量失效虚拟阵元,则其输出数据矩阵中存在大量整行缺失元素,破坏了阵列数据的完整结构,导致现有DOA估计方法精度下降甚至完全失效。
针对均匀线性阵列阵元失效下DOA估计精度下降的问题,文献[7]将单快拍阵列接收信号变换成一个等效低秩矩阵,利用矩阵填充(Matrix Completion,MC)方法求解核范数最小化问题对缺失数据进行填充,但由于该方法仅利用单快拍接收数据,DOA估计精度较低。文献[8]将阵列接收数据构造成二重块Hankel矩阵,并利用不定增广拉格朗日乘子法(Inexacted Augmented Lagrange Method,IALM)对失效阵元的缺失数据进行恢复。文献[9]针对冗余阵元失效场景下利用虚拟差分阵列中的冗余阵元对协方差矩阵中缺失数据进行填充,但当非冗余阵元失效时,虚拟差分阵列存在空洞,利用虚拟差分阵列无法有效恢复缺失数据,DOA估计性能有待提升。文献[10]提出冗余虚拟阵元和非冗余虚拟阵元失效场景下的阵元失效DOA估计方法,当冗余虚拟阵元失效时,利用差联合阵对失效阵元缺失数据进行填充;非冗余虚拟阵元失效时利用阵列冗余度结合MC算法对缺失数据进行恢复。针对存在阵元失效下MIMO雷达DOA估计问题,文献[11]提出一种基于差分共阵处理的协方差矩阵重构方法,但该方法要求发射阵元的间距为接收阵元间距的倍(其中为接收阵元数),因此并不能适用于任意结构的MIMO雷达,具有一定的局限性。文献[12]提出了一种基于块Hankel矩阵填充的MIMO雷达失效阵元缺失数据恢复方法,该方法利用MIMO雷达虚拟阵列协方差矩阵构造具有四重Hankel结构的低秩块Hankel矩阵,并利用MC方法填补块 Hankel矩阵中的缺失数据,得到完整的虚拟阵列协方差矩阵。然而在实际应用中,目标信号只占据空域少量角度分辨单元,目标相对于整个空间来说是稀疏的。因此,MIMO雷达虚拟阵列的采样数据矩阵不仅具有低秩性且还具有稀疏特性,联合利用低秩和稀疏先验,不仅能挖掘矩阵行间或列间元素的相关性,而且还能充分利用行内或列内元素的相关性,这为恢复阵元失效下MIMO雷达采样数据矩阵中的整行缺失元素提供了可能。
本文将MIMO雷达的阵元失效分为冗余虚拟阵元失效和非冗余虚拟阵元失效两种情况。当冗余虚拟阵元失效时,对空间上相同位置的正常工作冗余虚拟阵元数据取均值来填充失效阵元的缺失数据。当非冗余虚拟阵元失效时,针对利用虚拟阵列冗余度进行降维填充后的数据矩阵中仍存在整行缺失的数据问题,建立带有低秩和稀疏二重先验约束的矩阵填充模型,利用增广拉格朗日交替方向乘子法(Augmented Lagrange Method-Alternating Direction Method of Multipliers,ALM-ADMM)进行求解得到完整的降维数据矩阵。最后利用root-MUSIC算法估计目标DOA。仿真实验证明,本文方法能够有效提高阵元失效下MIMO雷达DOA估计精度。
1 阵元失效下MIMO雷达信号模型
假设MIMO雷达系统具有个发射阵元和个接收阵元,发射和接收阵列均为阵元间隔为半波长的均匀线阵。各发射阵元和接收阵元的归一化坐标分别记为{T,=-1}和{R,=-1},=1,2,…,,=1,2,…,。假设远场存在个非相干目标,它们的DOA分别为,,…,,第
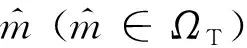
个发射阵元失效和第
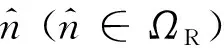


(1)
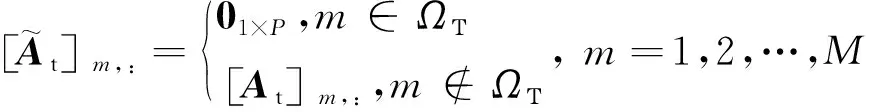
(2)

(3)

2 不同阵元失效场景下的DOA估计方法
2.1 冗余虚拟阵元失效下DOA估计
MIMO雷达冗余虚拟阵元失效情形如图1所示,假设接收阵列第2个阵元失效。由图1可知,空间上同一位置处具有多个冗余虚拟阵元,即使出现失效虚拟阵元仍有正常冗余虚拟阵元能够输出数据。因此,可以利用正常工作的冗余虚拟阵元对信号进行降维,将具有个虚拟阵元的虚拟阵列转换成具有+-1个有效虚拟阵元的等效阵列,实现对失效阵元缺失数据的填补。
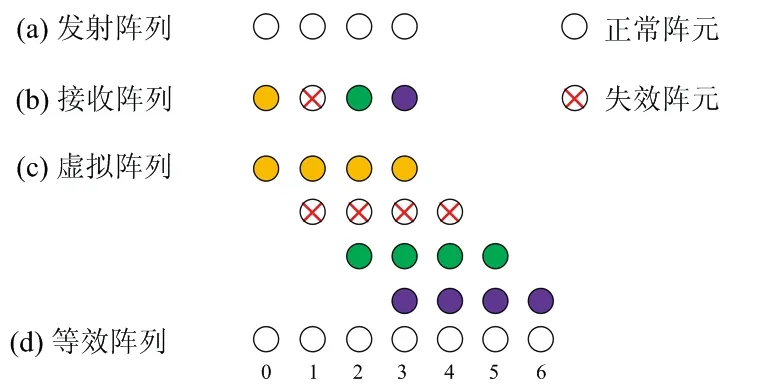
图1 冗余虚拟阵元失效场景
个虚拟阵元输出信号可以看成一个等效阵列的接收信号,则该等效阵列的阵元坐标可表示为
{=T,+R,|=1,2,…,;=1,2,…,}
(4)
定义集合表示位于空间上相同位置的冗余虚拟阵元编号集合,如下所示:
={(,)|T,+R,=}
(5)
为了降低计算复杂度,本文在降维过程中首先剔除失效虚拟阵元的零元素数据,然后对空间上位置为的正常工作的冗余虚拟阵元数据取均值处理,即
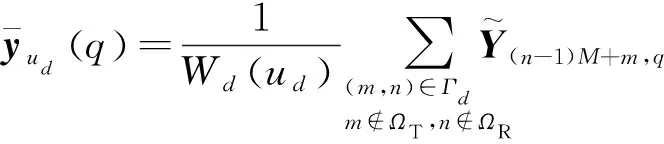
(6)
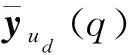
经过上述处理,不但能够利用虚拟阵列的冗余度对虚拟阵列输出信号进行降维,而且能对失效阵元的缺失数据进行填充,等效阵列的输出数据矩阵为

(7)
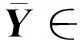
2.2 非冗余虚拟阵元失效情况下DOA估计
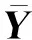

图2 非冗余虚拟阵元失效场景
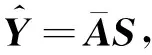
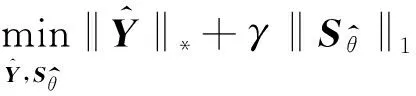
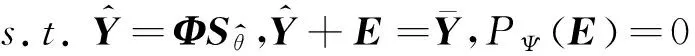
(8)
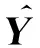
利用增广拉格朗日乘子法(ALM)并结合ADMM算法可以有效地求解式(8)中的优化问题。式(8)的增广拉格朗日函数可以表示为

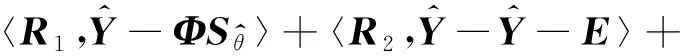
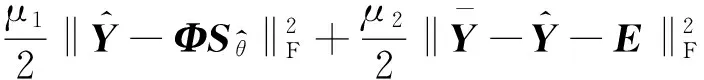
(9)
式中:,为拉格朗日乘子矩阵;,为惩罚因子;〈·〉表示两个矩阵的内积。
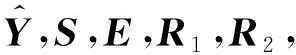
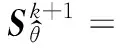
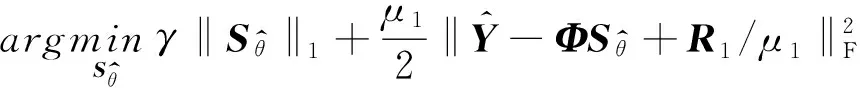
(10)
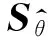
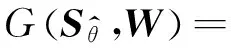
(11)
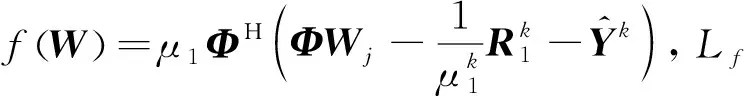
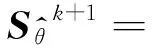
(12)

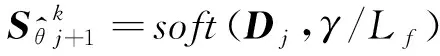
(13)
式中,(,)=sign()max{||-,0}为软阈值算子。近端变量的迭代如下:
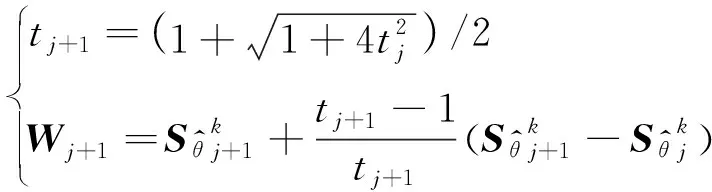
(14)

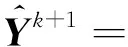
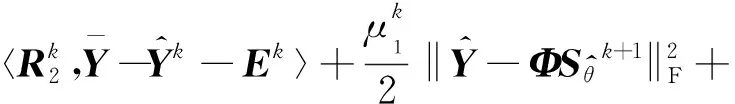
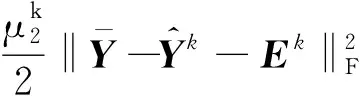
(15)
式(15)可以转化为求解如下优化方程:
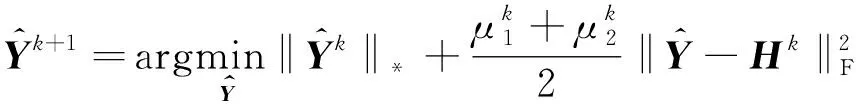
(16)
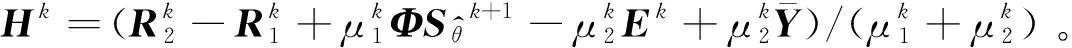
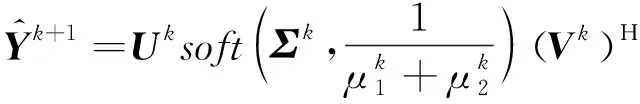
(17)
式中,,分别为的左奇异向量和右奇异向量,为由奇异值组成的对角矩阵,即=()。

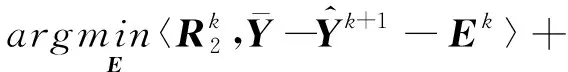
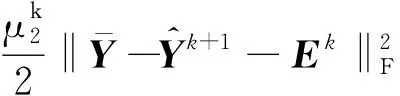
(18)
则的完整迭代解为
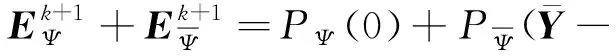
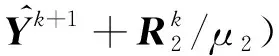
(19)
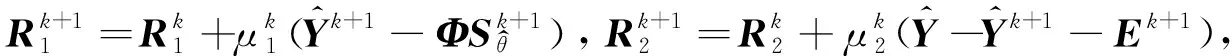

2.3 计算复杂度分析
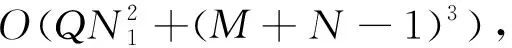
3 仿真实验
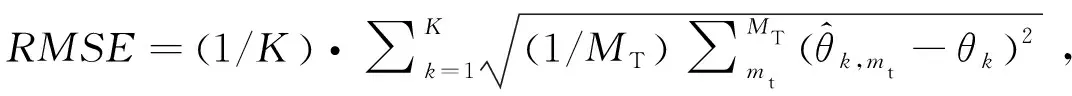
3.1 冗余虚拟阵元失效时DOA估计性能对比
假设发射阵列中第3个阵元失效,接收阵列中第2,5,9,11,14个阵元失效,快拍数为100,信噪比变化范围为-30~0 dB,进行100次蒙特卡罗实验,DOA估计均方根误差随信噪比变化如图3(a)所示。由图3(a)可知,当阵元失效时RD-root-MUSIC算法的目标角度估计误差明显大于阵元正常时的估计误差,表明MIMO雷达的传统降维预处理方法无法对失效阵元缺失数据进行有效填补。本文方法DOA估计性能要优于文献[10]方法和文献[12]方法,低信噪比时与阵元正常时的DOA估计性能接近,而在高信噪比时精度高于阵元正常的DOA估计精度。
假设信噪比为-10 dB,快拍数由50~350变化,其余参数与上述仿真实验一致,仿真结果如图3(b)所示。由图3(b)可知,随着快拍数的不断增加,所有方法的DOA估计性能都有所提升,在不同快拍数的情况下本文方法始终能保持最优,且DOA估计精度高于阵元正常时的估计精度。
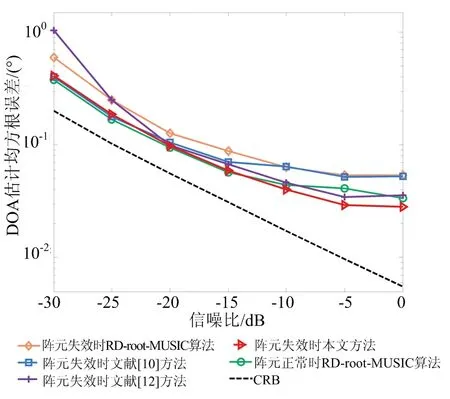
(a) DOA估计均方根误差随信噪比变化
3.2 非冗余虚拟阵元失效时DOA估计性能对比
假设MIMO雷达发射阵列第3个阵元失效,接收阵列第3,4,8,11,15个阵元失效,快拍数为100,仿真结果如图4(a)所示。由图4(a)可知,随着信噪比的增加,各种方法的DOA精度也随之提高,但本文方法估计的DOA更加趋近于阵元正常时的DOA,并且DOA估计性能明显优于文献[10]和文献[12]方法。图4(b)为目标角度估计均方根误差与快拍数的变化关系图,其中信噪比为-10 dB,快拍数由50~350变化,其余参数与上述实验一致。图4(b)中可以看出,本文方法的目标角度估计性能在不同快拍数下始终保持最优。

(a) DOA估计均方根误差随信噪比变化
4 结束语
当MIMO雷达阵列存在阵元失效时,虚拟阵列采样数据矩阵出现大批整行目标数据缺失,导致现有DOA估计算法性能下降甚至失效。针对此问题,本文提出了一种基于采样数据矩阵重构的MIMO雷达DOA估计方法。当冗余虚拟阵元失效时,利用空间上相同位置的虚拟阵元的冗余性对失效阵元缺失数据进行填充;当非冗余虚拟阵元失效时,由于利用阵列冗余度进行填充后采样数据矩阵中仍有整行元素缺失,因此构造带有低秩和稀疏先验约束的矩阵重构问题,利用ALM-ADMM算法进行求解实现对缺失元素的恢复。本文方法能有效避免因阵元失效带来的DOA估计性能下降的影响,具有较高的目标DOA估计精度。
