B2C模式下抚州农产品物流配送路径优化研究

宋月婵 SONG Yue-chan；黄晨 HUANG Chen

（①赣东学院，抚州 344000；②东华理工大学，南昌 330013）

0 引言

抚州市位于江西省中东部，自古为农桑富庶之地，素有“赣抚粮仓”之称，现代农业特色鲜明，有机农产品种类繁多，其中“南丰蜜桔、广昌白莲、崇仁麻鸡”等更是誉满海内外。农产品的销售及配送是决定抚州农业发展的一个重要环节，是促进抚州乡村振兴的重要途径，当前，农产品配送领域存在运输途中农产品易腐烂、损耗率高、资源利用不合理、物流成本高等缺陷，严重阻碍了抚州农业经济的科学化、现代化发展。

电子商务最早产生于20世纪60年代，是一种通过网络进行的商业模式，具有安全性、普遍性、低成本和高效率等特征，包括B2B、C2C、B2C三种模式。随着B2C电子商务在其他行业的广泛应用与快速发展，农产品的B2C电子商务模式也随之产生，该模式是指农产品电商企业通过农产品生产基地供给农产品，然后通过电子商务平台，以物流配送的方式向消费者进行销售。农产品电商的快速发展，使消费者可以更加方便、快捷地通过网络完成交易，提升了消费者的满意度。但由于抚州物流配送产业发展缓慢，抚州B2C模式下的农产品物流配送体系仍存在许多缺陷，例如随着消费者需求的变化，配送网络更加复杂，配送成本增加以及运输过程中农产品因腐烂引起的损耗等，这些因素已经严重阻碍了抚州农产品电子商务的发展，其中优化车辆路线是解决物流配送的关键环节，可以有效地降低配送成本，减少农产品损耗。因此，如何应用现代决策理论和数学方法，对B2C电子商务模式下物流的配送路线问题进行优化和布局不仅具有理论价值，而且有着至关重要的现实意义。为此，本文基于节约算法对B2C模式下农产品物流配送的路径问题进行分析研究，为抚州农产品的配送科学地规划配送路线，降低物流配送成本，减少农产品物流配送过程中的损耗，进而促进抚州农业经济的发展。

1 B2C模式下农产品物流配送路径优化模型

在B2C电子商务模式下，农产品的物流配送具有服务对象数量众多、客户位置分散等特点，物流配送体系极为复杂。因此如何科学合理的制定B2C模式下的农产品配送路径，提高资源利用率、降低物流配送成本，提高顾客的满意度，已成为抚州B2C电子商务发展的当务之急。车辆路径问题（Vehicle Routing Problem，VRP）是一类典型的物流配送优化问题，自1959年G.Danting和J.Ramser首次提出，便引起了运筹学、计算机应用、图论等领域学者的广泛关注与研究，并将其研究成果应用于物流运输系统等领域。经典的VRP问题定义为：对一系列发货点或收货点，组织调用一定数量的车辆，安排适当的行车路线，使车辆有序地通过它们，在满足货物需求量、交货时间、车辆容量限制等约束条件下，达到路程最短、费用最少等目标。

目前对VRP问题的求解方法分为两大类：精确算法和启发式算法，其中精确算法可求出其最优解，主要包括割平面法、分枝定界法等。但由于车辆路径优化问题是NP-hard问题，难以得到全局最优解，因此，启发式算法已成为学者研究的主流。启发式算法可求出组合优化问题的一个近似解，一般用于解决NP-hard问题，主要包括节约算法、遗传算法等。

1.1 B2C模式下物流配送的VRP模型

1.1.1 模型建立的基本思想

B2C模式下物流配送的VRP模型的基本思想描述如下：B2C电子商务企业通过Internet获取客户的订单情况，包括商品需求量、地理位置等，然后利用信息技术确定实际配送网络，要求在满足商品需求量、车辆容量限制等约束条件下，规划出最优的车辆配送路径，使得配送总距离最短。

1.1.2 模型建立

根据上述B2C模式下VRP模型建立的基本思想，建立B2C模式下物流配送路径优化的数学模型如下：

设现有一物流配送中心P，拥有M辆车，每辆车的载重量为q（=1，2，…，M），现向N个客户送货，客户为P，其对应货物需求量为r（i=1，2，…，N），配送中心到客户及各客户间的距离为d（i=1，2，…，N-1；j=1，2，…，N；i＜j；i=0表示配送中心），要求在同一天内完成配送并返回该配送中心。试确定所需车辆数K（K≤M）及各车辆的配送路线，使运输总距离z最短。

约束条件：

四要创新集体土地利用制度，研究农村移民承包地和宅基地资源资产化措施，推进承包地和宅基地市场化运作，让土地成为移民增收致富的新途径。

①配送所需要的车辆数不得大于该配送中心所能提供的车辆数；

②每条线路中客户的总需求量不能超过配送车辆的载重限制；

③每个客户的商品都需一次性配送到，并且仅由配送中心的一辆车进行配送；

④车辆从配送中心出发，完成任务之后都要返回到该配送中心。

决策变量如下：

数学模型：

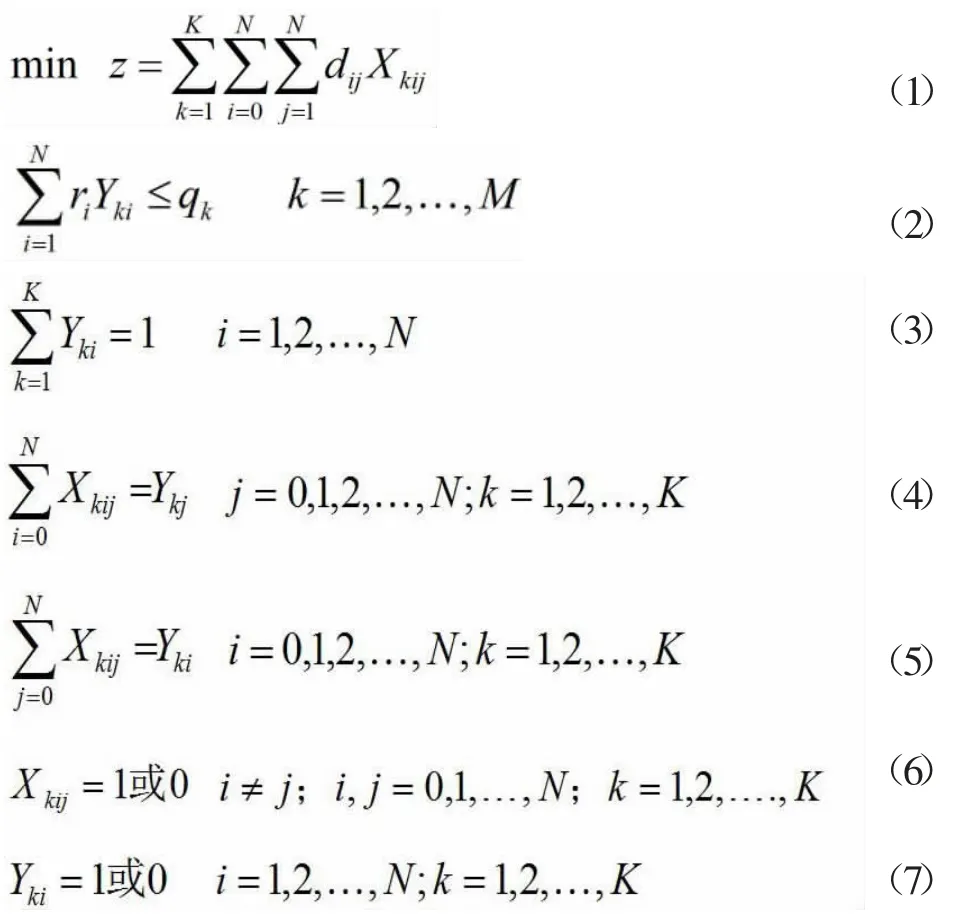
1.2 节约算法

1964 年Wright和Clarke首次提出节约算法，该算法是一种比较经典的启发式算法，用来解决车辆数目不确定的VRP问题。节约算法的基本原理为三角形任意两边之和大于第三边。设P为配送中心，现分别向配送点P和P配送货物，P到P和P的距离分别为d和d，两个配送点P和P的之间的距离为d，现比较两种配送方案，如图1的①和②所示。

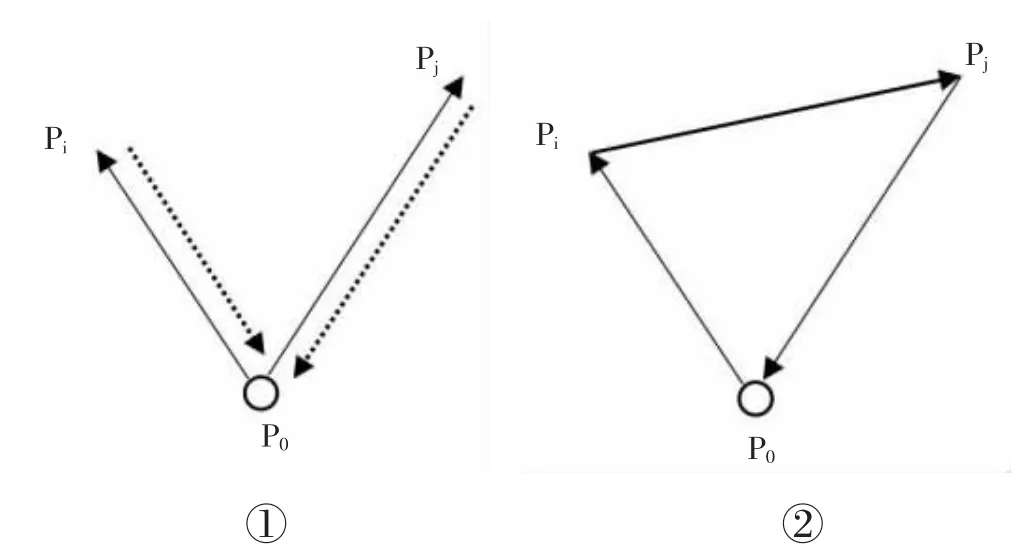
图1 节约算法

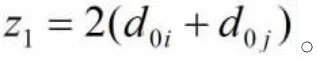
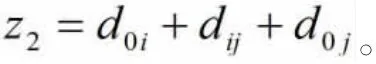
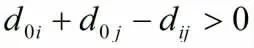
节约算法的基本步骤如下：

①求出配送网络中各节点之间的距离，得到配送里程表。

②根据公式（8），计算所有节点的节约里程数。

③将节约里程数按降序排序，得到配送节约里程排序表。

④在满足车辆最大载重限制的条件下，根据节约里程排序表，依次对回路进行合并，直到获得最优的配送路线方案。

2 案例分析

抚州某大型农产品电子商务企业位于抚州城区，该企业配送商品主要包括蔬菜、水果、禽蛋等农产品，其配送范围几乎覆盖抚州市各个区域，由于该公司物流配送系统不完善，主要采取一对一的物流配送方式，导致配送时间长、物流成本高、农产品在长时间配送途中损耗大，造成了资源的严重浪费。为此，本文应用节约算法为该企业进行车辆路径优化。

以抚州某大型农产品电子商务企业作为配送中心P，现向8个客户P（j=1，2，…，8）配送货物，假设配送中心有2台1吨和1台2吨的货车车型可供选用，配送成本为10元/公里，车辆固定出车费用为50元/辆。现应用节约算法为该企业制定最优的配送路线及车辆运行方案，使总配送费用最少。

①据调查，配送中心与客户的距离，客户之间的距离及客户的需求量如表1所示。

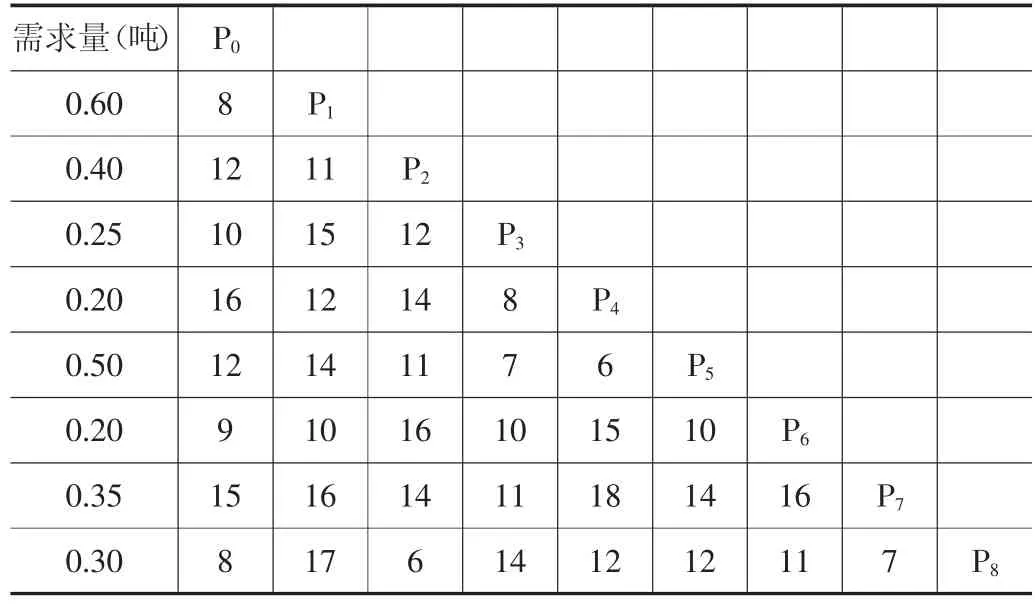
表1 配送里程表 单位：公里

②根据配送里程表，按照节约算法的计算公式，求出相应的节约里程数（表2括号内数字表示），计算结果如表2所示。

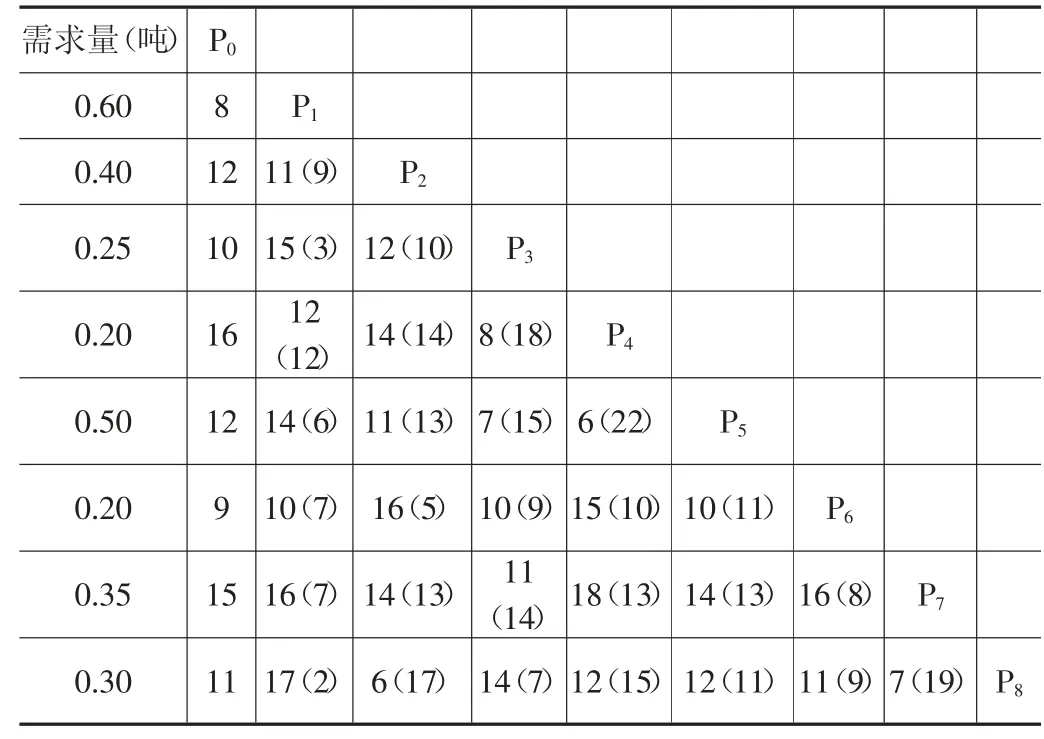
表2 节约里程表 单位：公里

③节约里程数按降序排序，排列结果如表3所示。

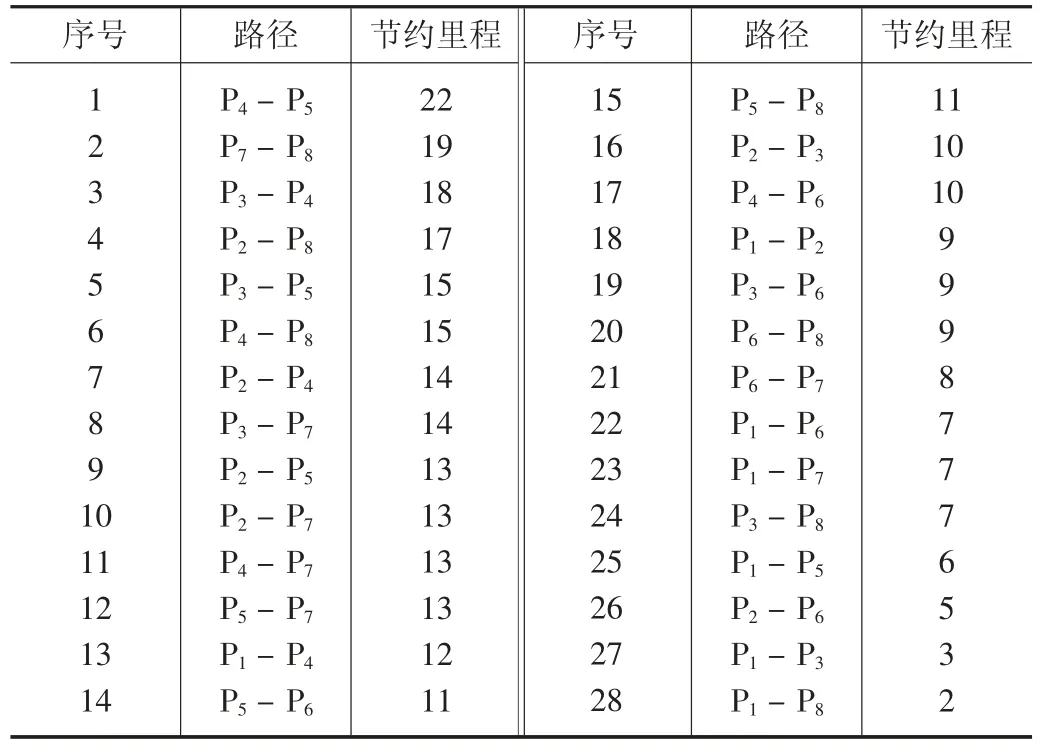
表3 配送节约里程排序表 单位：公里

④按照配送节约里程排序表，并根据车辆载重及客户需求量，不断修正配送路线，直到得到最优配送路线方案。首先确定初始配送方案，配送中心派8辆1吨的货车对每位客户采用一对一的配送方式进行送货，由此产生8条配送路线，总配送里程为2×（8+12+10+16+12+9+15+11）=186（公里）。然后，根据配送节约里程排序表，首先连接P-P，形成线路P→P→P→P，车辆载重达到0.2+0.5=0.7（吨），继续连接节点P，形成线路P→P→P→P→P，车辆载重达到0.2+0.5+0.25=0.95（吨），满足车辆载重限制，因此，确定第一条配送路线：P→P→P→P→P，以此类推，依次对剩余节点进行合并，进而获得最优配送路线方案，如表4所示。

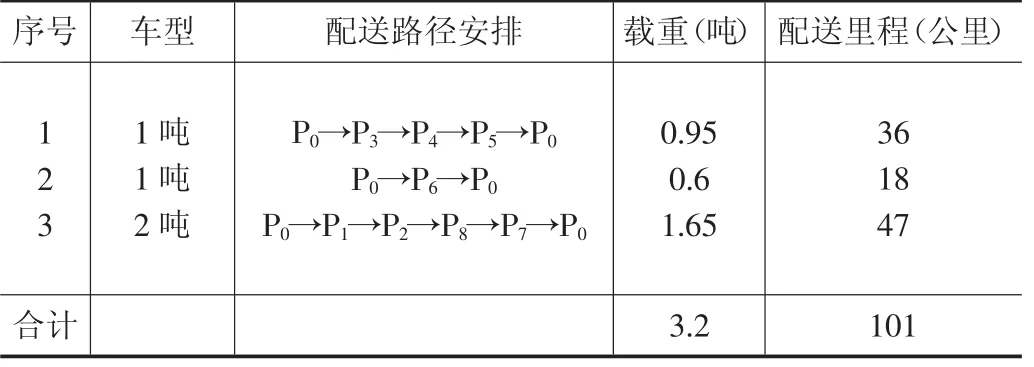
表4 最优配送路线方案

由表4可以看出，线路优化前，抚州某大型农产品电子商务企业对每个客户都采用一对一的配送方式，配送车辆为8辆1吨的车型，总配送里程达到186公里，配送总费用为2260元。经过节约算法优化后，配送路径为三条，配送车辆为2辆1吨和1辆2吨的车型，配送总里程为101公里，配送总费用为1160元，优化后的配送方案共节约配送里程为85公里，节约总配送费用为1000元。

由此可见，通过节约算法优化后的配送路径规划方式，解决了迂回运输和重复运输等问题，不但节约了配送的时间，而且有效降低了物流配送的成本，做到资源的合理利用，实现物流科学化，对抚州农产品的物流配送提供理论指导意义。

3 结语

在电子商务快速发展的大背景下，农产品的物流配送逐步实现了科学化、系统化，但产业发展仍处于探索阶段，B2C模式下抚州农产品的物流配送仍然存在物流配送系统不完善，物流配送路径不合理等问题，为此本文建立了B2C模式下以配送总距离最短为目标的VRP模型，并将该模型对抚州某大型农产品电子商务企业进行实证研究。仿真结果表明，应用节约算法优化后，不仅配送距离明显缩短，而且节约了总的配送成本，提高了物流的总体效益。因此，该模型为优化抚州农产品物流配送路径不仅提供了理论支持，而且具有十分重要的现实意义。但实际的农产品物流配送过程更为复杂，例如配送中心不止一个，车辆种类繁多，客户对送货时间有具体要求等，这些将是今后进一步的研究方向。