采用透水排桩对河道影响的数值模拟分析

刘恒博

(新疆维吾尔自治区塔里木河流域干流管理局，新疆 库尔勒 841000)

可作为河道整治结构的建筑物种类繁多，有护堤、沟坝、护岸、堰等，通过相关防护措施可减少河岸侵蚀[1-4]。近年来，我国大力倡导保护河流生态系统的多样性，恢复退化河流的鱼类栖息地[5-6]。

丁坝周围多样化的水流创造了适合河岸植被和水生生物生存的条件，大多数学者研究了各种构筑物对河道的冲刷规律，傅宝龙[7]针对新疆地区的山溪性河流特点，提出了同时考虑河势现状和演变趋势的河道整治原则，包括布置顺坝、护岸或丁坝；黄春花[8]提出河道综合治理重点应从河道景观、水质修复治理和生态护坡三方面出发；黄建权[9]利用二维泥沙控制方程，对冲淤和河床变形进行模拟，得出结论：经整治后对流量和潮位影响甚微，但可增加断面面积增强过流能力。

以上研究主要集中在稳定水流的局部冲刷深度和速度分布上，并且对其他类型的结构在河道整治中的应用鲜有对比分析。本文提出一种透水排桩结构(分为全透水和半透水排桩)，用于改善塔里木河水流状态。其中半透水排桩结构的特征是在其下方有一个开口(可通过部分水流)，允许流速降低的水流通过此结构，并使泥沙在河岸附近沉积，而上部(不透水部分)封闭，导致近地表水流流向主河道方向。

为了分析透水排桩对水流动力和河道形态的影响，通过室内试验和数值模拟对河道治理构筑物进行了分析，对比不透水丁坝和透水排桩结构，研究了三种类型的结构物在非淹没条件下对流场和河床变形的影响。

1 室内试验

1.1 试验装置

试验研究在乌鲁木齐试验室进行，水槽长10m，宽0.80m，深0.28m(试验区深0.45m)。试验装置见图1。河道坡度为1/800。凹槽附在水槽钢壁上，在水槽活动部分之前，在上游设置距水槽底部0.1m、长1.0m的假底板，以减小水面变化。在水槽入口安装了Ⅴ形缺口堰，用来测量流入流量(见图1)。水槽水深由位于下游端的钢制后挡板调节。使用精度为±0.5mm的游标卡尺测量水位。

图1 试验设置(单位：cm)

1.2 试验过程

试验采用的水力条件见表1，每次开始试验之前，水槽由下游的塑料管慢慢灌满水。一旦达到所要求的水深和流量，试验就在该冲刷条件下进行。冲刷深度随所研究结构的不同而变化。用盾构图确定沉积物(煤)物质的临界剪切速度u*c。

表1 试验方案

试验运行时间为6h，然后，流量逐渐减少，防止河床物质移动。为了确定最终的河床变形轮廓，仔细地从水槽中排空剩余的水，并使用型号为LK-2500的激光位移传感器测量不同断面的冲刷深度。在变形床面测量后，立即将水泥粉均匀地撒在冲刷床面上以固定床面，将充分浸渍水泥粉的沉淀物干燥24h。

采用电磁测流仪测量三维速度分量，电流计的I形探头测量水平方向(X-Y平面)的速度，另一个L形探头测量垂直方向(X-Z平面或Y-Z平面)的速度，连接到模拟/数字信号转换器。探头放在水中，通过游标卡尺固定，以确定所需位置的速度，通过连接电脑来存储测量数据。

X轴、Y轴和Z轴见图1。不透水丁坝由1.5cm厚的木制长方体制成，透水排桩由一系列直径为0.6cm的钢圆棒制成，设计透水率为50%，并用钢板堵塞上半部分来代表不透水部分。试验分三种方案进行，分别为案例1、案例2和案例3，对应不透水丁坝、全透水排桩和半透水排桩；在不透水边界条件下测试，三种排桩的测试条件完全相同，见表1。

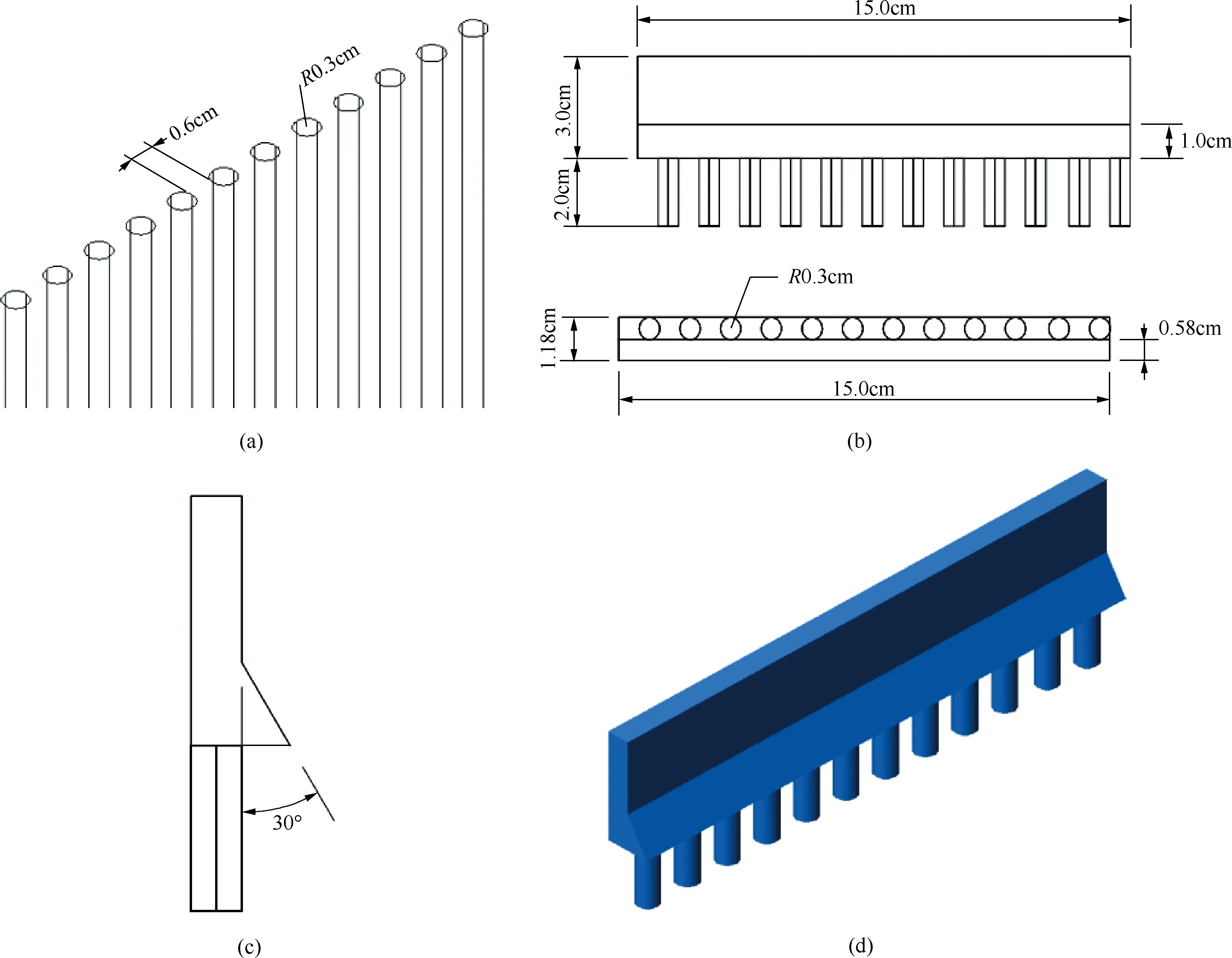
图2 透水排桩结构

2 数值模拟

2.1 水动力模型

流动计算的控制方程是基于三维的平均雷诺方程和连续性方程，连续性方程的张量表示为

(1)

(2)

式中ui——时均速度分量(i=1,2,3)；

xi——坐标分量；

ρ——流体密度；

Fi——体积力；

p——时均压力；

υ——流体的运动黏度；

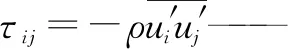
u′i——脉动速度分量，湍流采用k-ε模型。

通过线性本构方程得到雷诺张量：

(3)

式中k——湍流动能；

υt——涡黏系数；υt=Cvρk2/ε，Cv为常量，ε为单位流体脉动功能的耗散率；

Sij——应变率张量；

δij——变形速度张量。

在模拟中，将入口边界视为狄利克雷边界，并给出了所有的数值。出口边界设置在远离凹槽区域的地方，假设在那里有一个零梯度的第二类边界。在不透水边界处采用壁面函数法，排桩的上封闭区和下透水开口用一些细网格表示，仿真过程遵循半隐式连接压力法计算流体动力学方程[11-12]。

2.2 沉积物运移模型

明渠中的泥沙输运由泥沙质量平衡方程在水深h上的积分控制：

(4)

式中zb——基准面以上的局部层位；

λ——河床孔隙度；

qTx、qTy——总输沙量在x和y方向的分量；

E——向上的近床流；

D——向下的近层通量。

为了计算输沙率，将其细分为床沙和悬沙。

用芦田-美惠的经验公式计算河床输沙量。

(5)

式中qb——河床荷载；

s——沉积物比重；

d——沉积物直径；

τ*、τ*c、τ*e——无量纲切应力、临界切应力和有效切应力；

u*、u*c——摩擦速度和临界摩擦速度。

3 结果和讨论

3.1 速度分布

3.1.1X-Y平面结构体周围速度分布

水平面内不同类型结构周围实测和计算的流速分布结果见图3～图4。在案例1(见图3)中，当水流接近上游的丁坝时，流向主河道的阻塞流在丁坝顶部前形成了混合区。该水流流向下游，在丁坝之间以及在河岸附近的丁坝下游形成再循环流。通过对实测结果和模拟结果的比较，发现不透水丁坝周围的流动规律非常相似。由于在模拟计算中对网格进行了细化，可以清楚地看到两个丁坝之间的再循环流，以及上游丁坝头部的流动分离。

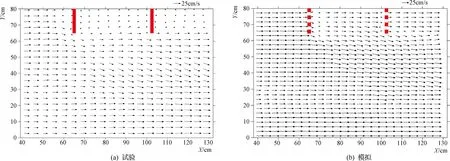
图3 案例1：不透水丁坝在水平面上的流速

与不透水丁坝有很大的不同，全透水排桩模拟结果表明(见图4)，水流方向没有发生很大的变化，实际上与水槽方向平行。试验结果和模拟结果均表明，流向全透水排桩头部主河道的水流方向，由于透水性的影响，水流强度较小。在排桩上游方向，靠近河岸处速度会减小；在水流经过下游后，速度减小更明显，这对河岸形成了保护作用。

在观察半透水排桩时，由于水流通过较低的开口，可以观察到水流形态的差异，特别是在两个排桩结构之间的区域。从图5可以看出，水流经过上游结构后，流向主河道方向，阻止了二次流的形成。此外，由于上半部分不透水挡板导致的流动分离，使近地面的流动偏离主河道方向，速度也会降低。

图5 案例3：半透水排桩在水平面上的流速

3.1.2Y-Z平面和X-Z平面截面速度分布

通过分析见图6～图9的横断面和纵断面的速度分布，可以更详细地了解结构周围复杂的三维流速分布。比较了半透水排桩和不透水丁坝情况(案例1和案例3)，分析这些结构对流型的影响，典型的流型主要包括泡状流、弹状流、分层流、波状流及环状流。对X=62.0cm(横截面)分析，距离上游结构仅2.25cm，Y=72.0cm(纵截面)位于结构中部。

图6 案例1中不透水丁坝在X=62.0cm处的流速

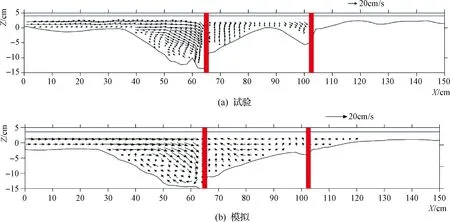
图7 案例1中不透水丁坝在Y=72.0cm处的流速

图8 案例3中半透水排桩在X=62.0cm处的流速

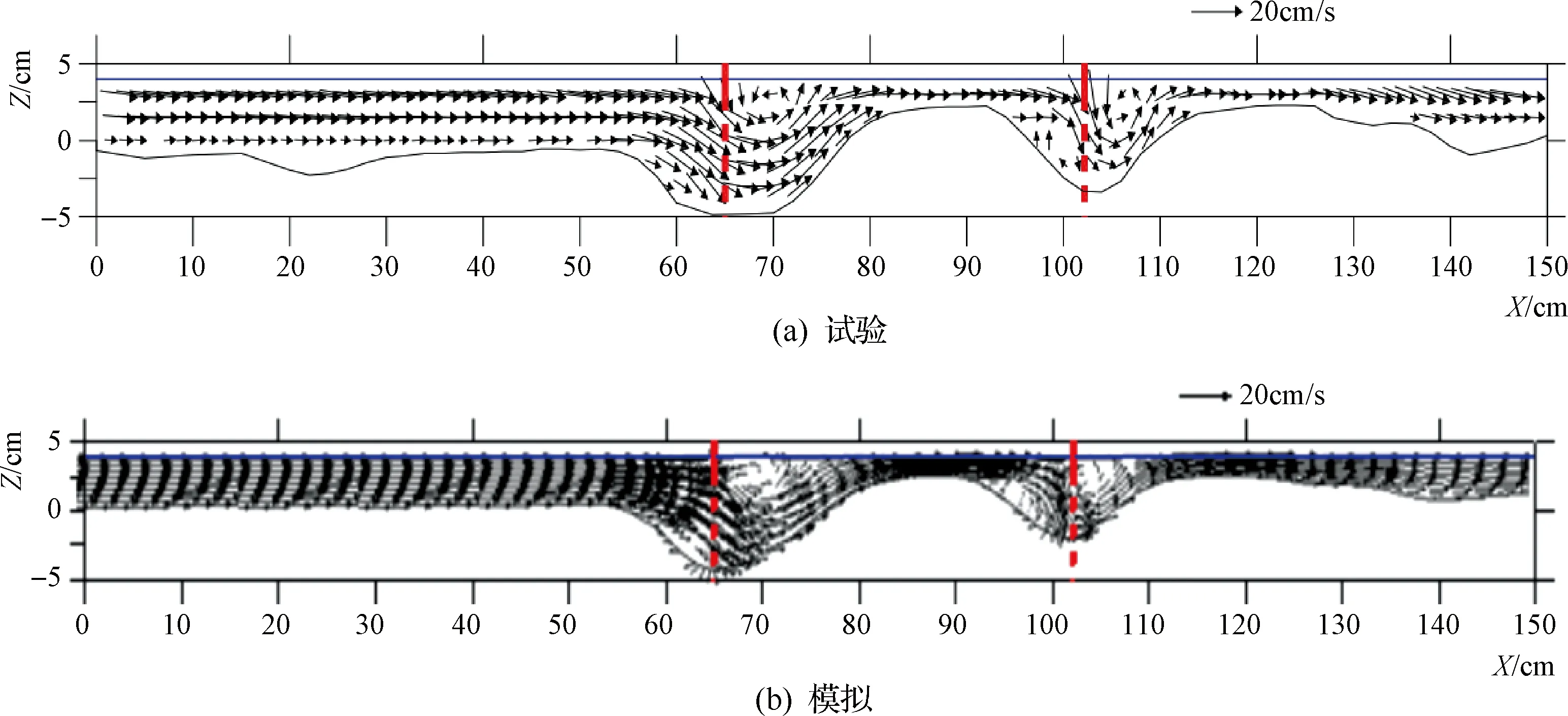
图9 案例3中半透水排桩在Y=72.0cm处的流速

在两种情况下，由向下流动引起的上游结构附近形成的垂直涡与计算结果非常相似。然而,半透水排桩在近地表向主流道偏移的情况下流速更高，这比不透水丁坝情况更有效，因为上弯曲板可将近地表流引导到主流道，减小了对结构附近床层的影响。纵向截面清楚地显示了在两个不透水丁坝结构上游的向下水流，这导致在结构上游形成涡流。在每个结构的下游，通过低渗透部分的流速降低表现出类似的小幅度垂直涡，会增加那里的沉积过程。

3.2 河床变形

图10和图11分别为案例1和案例2平衡条件下河床等值线试验结果与模拟结果的对比，半透水排桩(案例3)的试验结果见图12。

图10 案例1中不透水丁坝床面等高线

图11 案例2中全透水排桩床面等高线

图12 案例3中半透水排桩床面等高线

案例1中由于堵塞流而形成的向下通量是上游地区冲刷最深的主要原因，在模拟结果中可以验证这一特征[见图10(b)]。

案例3为半透水排桩，上部弯曲板向主河道方向的高速近地表流动和通过下部的流动，减小了下行流量的影响，在全透水排桩中也存在同样的影响。在试验和模拟中，由于与半透水排桩相比，流速减小幅度较小，因此导致的侵蚀比其他情况都小(见图11)。

在案例1[见图4(a)]中可以看到流动分离，这是在排桩之间区域形成再循环流的原因，导致了图10(a)和图10(b)中观察到的河岸侵蚀。见图10，在排桩下游，河岸附近的低速回流导致泥沙淤积。

类似的水流分离也发生在半透水排桩中(见图5)，由于表层水流受阻碍作用和底层水流经下部透水区，不能形成循环流，降低了河岸附近的侵蚀强度。因此，该结构可用作河岸防护。

4 结论与展望

本研究提供了非淹没条件下半透水排桩周围流型和河床变形的有关规律，在相同的水力条件下，考虑结构周围的流速分布和河床变形，对不透水和透水的结构进行了研究，以验证其与半透水排桩的异同，主要得到以下结论：

a.分析了半透水排桩构造对泥沙输运过程的影响规律，结构体周围的水流形态变化和河岸附近的沉积可以保护主河道不受侵蚀，而主河道的侵蚀强度增加会导致河流中形成更深的沟。

b.数值模型的计算结果对各种情况下的流型都有较好的一致性，特别是在全透水排桩和半透水排桩等复杂结构周围的流动。通过对泥沙沉积进行计算，可预测河床变形。

c.半透水排桩作为一种有效的河道整治措施，可以替代传统的丁坝结构。

d.在试验中观察到的结构附近的悬移质，需要在泥沙输运模型中加入悬浮泥沙计算进行研究，且需对相同的结构进行水下模拟。