三相短路电流计算程序在水利工程中的应用

薛 媛

(湖北省水利水电规划勘测设计院，湖北 武汉 430070)

电力系统在运行中会产生各种系统故障，其中最严重的一种就是电力系统短路。在实际工作中，涉及有关电力系统和电气设备设计的内容，特别是在电气一次主接线方案设计、电气设备和载流导体选择、电气二次继电保护的选择和整定计算等方面，都需要进行短路电流计算。

工程设计人员在进行电气方案设计中，通常是采用《电力工程电气设计手册》中的“短路电流计算”方法来计算。此方法为人工计算，不但计算工作量大，而且在进行Y/△变换及有环形网的网络化简时极易出错，效率不高。

目前市面上《短路电流计算程序》很多，功能也很强大，但所需要的原始数据较多，这些数据在水利工程可行性研究阶段和初步设计阶段很难收集齐。另外这些“程序”推广使用需要进行专门的培训，一段时间不使用又会遗忘。这些“程序”不能被广大电气设计人员所采用。因此，开发一种既适用于工程实际设计阶段又方便设计人员操作的短路电流计算程序显得重要而急迫。

1 三相短路电流计算程序的研发

1.1 数学模型的建立过程

我们研究电力系统运行状态时通常会将其转换成数学问题，并通过建立数学模型来分析描述。短路电流计算一般用恒定参数的电路表示线路和变压器，用给定电势源的恒参数支路表示发电机，用恒定阻抗表示负荷，这样电力系统的等值网络就转化成了一个线性网络，而线性网络的数学模型为一组线性代数方程组。我们在进行短路电流计算时，需要将原始数据转换成与线性代数方程相对应的形式，即形成节点导纳矩阵。

具体做法是先将各电气节点(母线)编号，然后将网络中各支路(如变压器、电抗器、线路等)化成标幺值再编号。最后将发电机及系统编号。计算方法是先把网路中的电压源化成电流源，并以标幺值的形式注入对应的节点上。网路中各支路采用导纳，根据注入各节点电流的代数和为零，可以列出下式：

∑Yij(Vi-Vj)+Yij-Ii=0

(1)

式中Yij——两节点之间的导纳；

Vi、Vj——节点电压；

Xji——电源的内阻。

整理上式得

〔Y〕〔V〕=〔I〕

(2)

式中 〔Y〕——已知的n×n阶方阵；

〔I〕——已知的n×1阶列阵。

该方程组为线性方程组。可用高斯消去法或约当消去法求解，求出〔V〕n×1阶列阵，即各节点的Vi、Vj电压值。按串联电路中电流处处相等的原理，第i节点上的电源点到D点的直连电抗为

(3)

从上式的推导可知，在同一网络中，由于电源点注入的电流值不一样，该节点的电压就不同，直连电抗值也就变了。求得直连电抗后，再查曲线即可求得有名值。

1.2 数学模型的程序实现方法

1.2.1 节点编号顺序优化

根据《电力系统分析》相关章节的知识，我们知道节点的编号反映了高斯消去法的消元次序，也代表了星网变换时的节点消去次序。为了减少注入元的数目，我们应该尽量避免先消节点出现大量新增支路的情况，所以节点编号顺序优化的原则是消去时增加新支路最少的节点应该优先编号。

优化编号分为静态和动态两种，如果网络的原始接线图算出每一节点的连接支路数或新增支路数在整个编号过程中保持不变，则称这种优化编号为静态的；如果在节点编号过程中，每消去一个节点，未消节点的连接支路数或新增支路数都要随着网络接线的变化而进行修改，则称这种优化编号为动态的。

本文介绍的三相短路电流计算程序采用半动态优化处理。首先对出线最少的节点优先编号，当节点未编号时，未去掉支路节点编号小的先编。接着对节点出线数相等，与所消去节点相连的节点先编，若均与已编号节点相连，则与先编号节点相连的先编。最后将已编号节点相连的所有支路去掉，加上注入元支路，再对出线最少的节点编号。

1.2.2 因子表法求阻抗矩阵和电流

首先将等值网络的原始数据形成节点导纳矩阵，只存上三角元素(电力系统为对称矩阵)，节点所有相连的阻抗倒数(节点的自导纳)为三角的对角元素；节点间的阻抗倒数(节点的互导纳)为三角形的非对角元素。此时节点电压方程为

I=YV

(4)

式中I——节点注入电流列向量；

V——节点电压列向量；

Y——节点导纳矩阵。

因为

Z=1/Y

(5)

则导纳矩阵的逆矩阵(阻抗矩阵)为

V=ZI

(6)

由上式可知，当电流为单位值时，节点电压即节点阻抗。

在不计负荷(或负荷短路电流小得多)的简化短路电流计算中，假定故障前节点电压标幺值为1，并忽略正常通过支路的电流，相当于计算发电机电势为零，仅在故障点加一极性相反标幺值为1的电势时的故障点短路电流。

由式(6)：

任一支路电流为

(7)

式中Zid——节点i与节点d的互阻抗，阻抗Z矩阵d列元素；

Zjd——节点j与节点d的互阻抗，阻抗Z矩阵d列元素；

yij——节点i与节点j的互导纳。

我们仅需解得元素Zid，Zjd，Zdd，即可求得电流。这些元素都处于阻抗Z矩阵d列，可以通过式(8)对Y求解d列逆阵。

(8)

对短路点取1求解y逆，就是因子表在给定短路点1(其余点为0)的回代过程，得短路点的d列元素。

同理，分支电流按公式简化为

(9)

式中Zi,Zj,Zdd——求逆中的d列元素；

Zij——相应回路的阻抗。

每个电源点供给的短路电流为短路点与电源点的连接阻抗，即电源支路的自阻抗Zij。

1.2.3 求计算电抗

将电源支路电流的倒数(转移电抗)折算为以该电源容量为基准的计算电抗,通过式(10)求得计算电抗，进而求得任意时刻的短路电流值。

Xjs=XjdSe/Sj

(10)

2 三相短路电流计算程序计算结果分析

选取一个具体的水利工程实例，分析三相短路电流计算程序计算结果是否正确。已知土司港泵站10kV系统电抗标幺值为0.149，线路电抗标幺值为1.37，同步电机电抗标幺值为4.275，得到泵站系统阻抗图(见图1)。

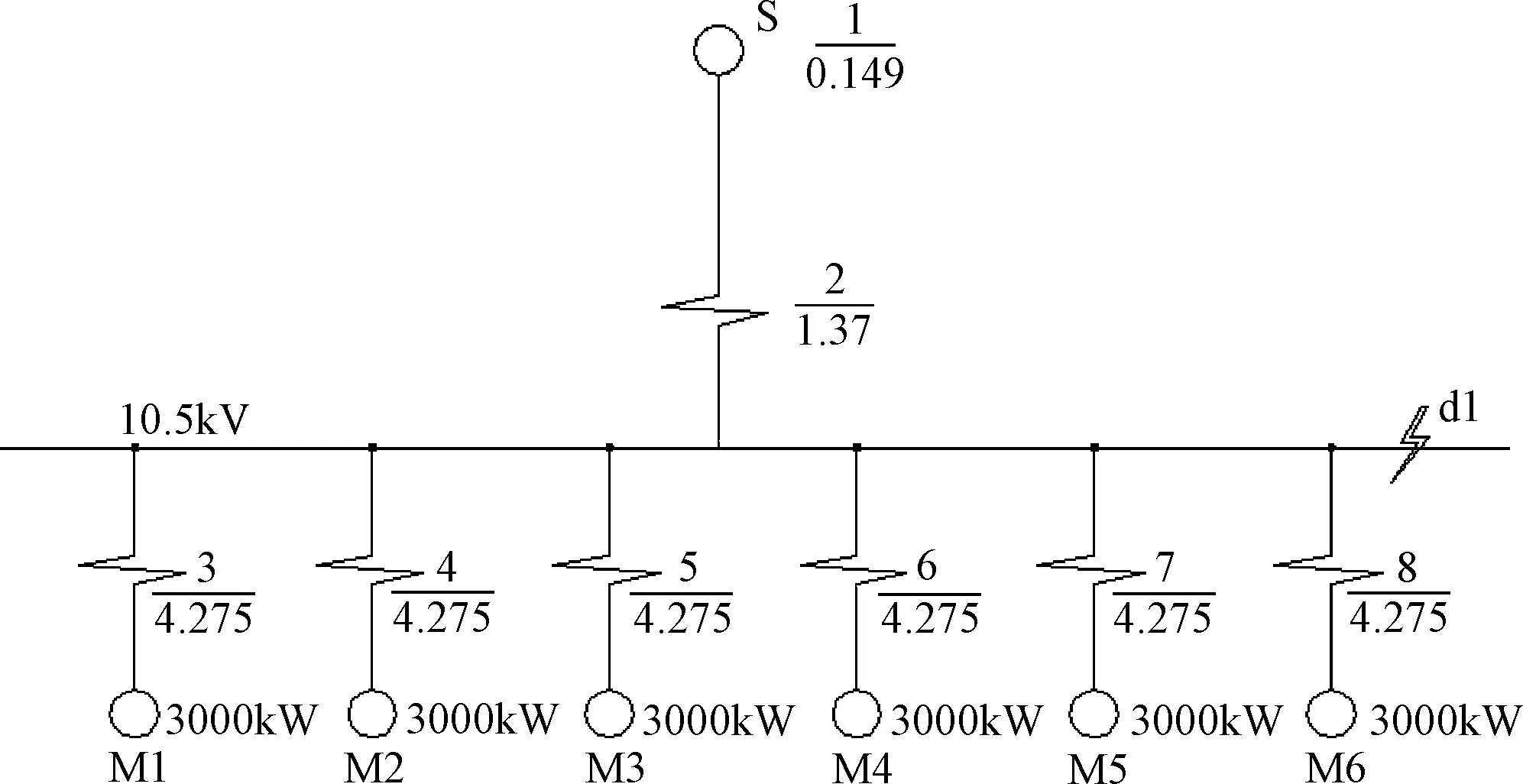
图1 泵站系统阻抗

将短路容量和各电源点至节点的电抗标幺值等原始数据输入计算程序，通过运行程序得到系统和六台电动机在不同时刻的短路电流值，结果见图2。

图2 短路电流计算结果

经验证，程序计算出的短路电流值和手工计算出的结果非常接近。由此可见：此程序计算结果准确可靠，计算精度满足设计要求。

3 三相短路电流计算程序的操作方法和优越性

3.1 程序的操作方法

a.通过浏览器登录网站http://192.168.114.79 /SC/index.asp，进入短路电流计算程序界面，见图3。

b.在计算程序界面中输入电源点名称、短路容量等原始数据，输入完成后点“提交”，见图4。

图4 短路电流计算程序数据输入界面

c.运行短路电流计算程序进行计算，得出短路电流计算结果表。

3.2 程序的优越性

a.该网络版三相短路电流计算程序在有网的环境下随时可以运行，不受局域网的限制；不需要安装任何软件安装包，节省了电脑的硬盘容量。

b.相对于其他三相短路电流计算程序，该计算程序所需的原始数据较少，计算前期准备工作较简单，非常适用于工程可研阶段和初设阶段；程序操作简单方便，功能实用，易懂易学，很容易被广大电气设计人员所接受。

c.对于水利水电行业的设计工作，该三相短路电流计算程序从实际工作内容出发，简化了计算过程，减少了设计工作量，计算精度满足设计要求。

4 结 语

近几年国家对水利行业投入的资金增大，推进了水利基础设施建设，同时对工程设计周期和设计质量提出了更高的要求。针对早期短路电流采用手工计算，工作量大且极易出错的情况，设计院研发了这款网络版三相短路电流计算程序。程序操作步骤简单，结果准确可靠，值得在水利设计工作中推广和应用。

目前该程序只能进行三相短路电流计算，不能适用于不对称短路电流的计算，因此适用范围有一定的局限性，在今后的研究中还需进一步升级。