Research on the On-orbit Background of the Hard X-Ray Imager Onboard ASO-S

Wei Liu ,Deng-Yi Chen,Xian-Kai Jiang,Jian Wu,Zhe Zhang,Yi-Ming Hu,Yang Su,Wei Chen,and Tao Ma

1 Key Laboratory of Dark Matter and Space Astronomy, Purple Mountain Observatory, Chinese Academy of Sciences, Nanjing 210023,China; wujian@pmo.ac.cn

2 School of Astronomy and Space Science, University of Science and Technology of China, Hefei 230026, China

Abstract The space environment background of various particle fluxes of the Hard X-ray Imager(HXI),one of the payloads of the Advanced Space-based Solar Observatory (ASO-S) spacecraft, is investigated and presented. Different approaches are used to obtain the input information on various space environment particles (protons, alpha particles,electrons,positrons,neutrons,and photons).Some special regions(SAA and radiation belt)are also taken into account. The findings indicate that electrons are the primary background source in the radiation belt. Due to the large background flux generated by electrons,HXI cannot effectively observe solar flares in the radiation belt.Outside the radiation belt,primary protons and albedo photons are the main sources of background at low and high magnetic latitudes respectively.The statistical analysis of the flare and background spectra shows that the errors of the flare energy spectrum observation are mainly concentrated in the high energy band,and the detector still has a certain spectrum observation capability for flares of C-class and below in the low energy band of the non-radiation belt. The imaging observation of flares of C-class and below is significantly affected by the accuracy of background subtraction. The energy band with the best signal-to-noise ratio is from 10 to 50 keV, which can be used to monitor the formation and class of flares.

Key words: instrumentation: detectors –Sun: X-rays –gamma-rays –X-rays: diffuse background –(cosmology:)cosmic background radiation

1. Introduction

The Advanced Space-based Solar Observatory (ASO-S) is planned to observe simultaneously the solar magnetic field,coronal mass ejections(CMEs),and solar flares,as well as study the origin of these three phenomena and the possible causal relationship between them, which is a fundamental scientific problem in modern solar physics. To achieve these goals, the ASO-S mission carries three payloads: the Full-disk MagnetoGraph (FMG) for the solar photospheric magnetic field,the Lyα Solar Telescope (LST) for CME observation, and the solar Hard X-ray Imager (HXI) for solar flare imaging observation. The unique combination of these payloads enables simultaneous observations of the full Sun’s vector magnetic field,imaging spectroscopy at high energies of solar flares, and formation and evolution of solar flares and CMEs on the disk and in the inner corona (Gan et al. 2019).

Solar flares, as the most extreme energy bursts in the solar system,are one of the few astronomical occurrences that can even affect our daily life and have thus been the focus of astronomical research (see the reviews on flares in Priest & Forbes 2002;Fletcher et al. 2011; Shibata & Magara 2011; Benz 2017). The formation of flares is the release of stored magnetic energy via magnetic reconnection and other mechanisms. The released energy produces electromagnetic radiation that spans the entire spectrum from radio, infrared to X-rays and gamma-rays. The nonthermal bremsstrahlung radiation of accelerating electrons is the primary source of hard X-rays in flares.Imaging observations of solar hard X-rays are widely employed in the study of flares,particularly in the diagnosis of plasma heating, particle acceleration, magnetic reconnection, and so on (Su et al. 2019). HXI is proposed to measure the X-rays from the Sun between 30 and 200 keV and obtain spatial and energy distribution information,allowing imaging of solar X-ray sources in different energy intervals (Zhang et al. 2019).

To perform X-ray imaging, HXI employs the spatial modulating Fourier-transformation technique that is often used in the same kind of high-energy imaging instruments, like YOHKOH/HXT (Kosugi et al. 1991). HXI is comprised of a collimator, a spectrometer, and an electric control box. The collimator is made up of front and rear parallel grid plates.The front grid plate is oriented toward the Sun. On the grid plate,grid pairs with varied pitches and placement angles are placed to produce 91 groups of sub-collimators to accomplish X-ray modulation, which can acquire spatial distribution information of incident photons and is utilized in conjunction with the spectrometer to achieve X-ray imaging. The field of view(FOV) of HXI is determined by the front and rear grid size,which is approximately 40′. The spectrometer is a scintillator detector made of lanthanum bromide (LaBr3) that is placed behind the collimator to detect the X-ray energy modulated by the collimator. The LaBr3crystal is doped with 0.5% cerium,and its size is Φ25 mm×25 mm. The high-energy photons from the Sun pass via the collimator before entering the LaBr3crystal and interacting with the crystal’s atoms to deposit energy. In the crystal,the deposited energy is transformed into fluorescence. The photocathode collects fluorescence through the light path and generates photoelectrons. Electronic instruments turn the photoelectrons into electrical impulses, which are then measured by electronic instruments to be detected.

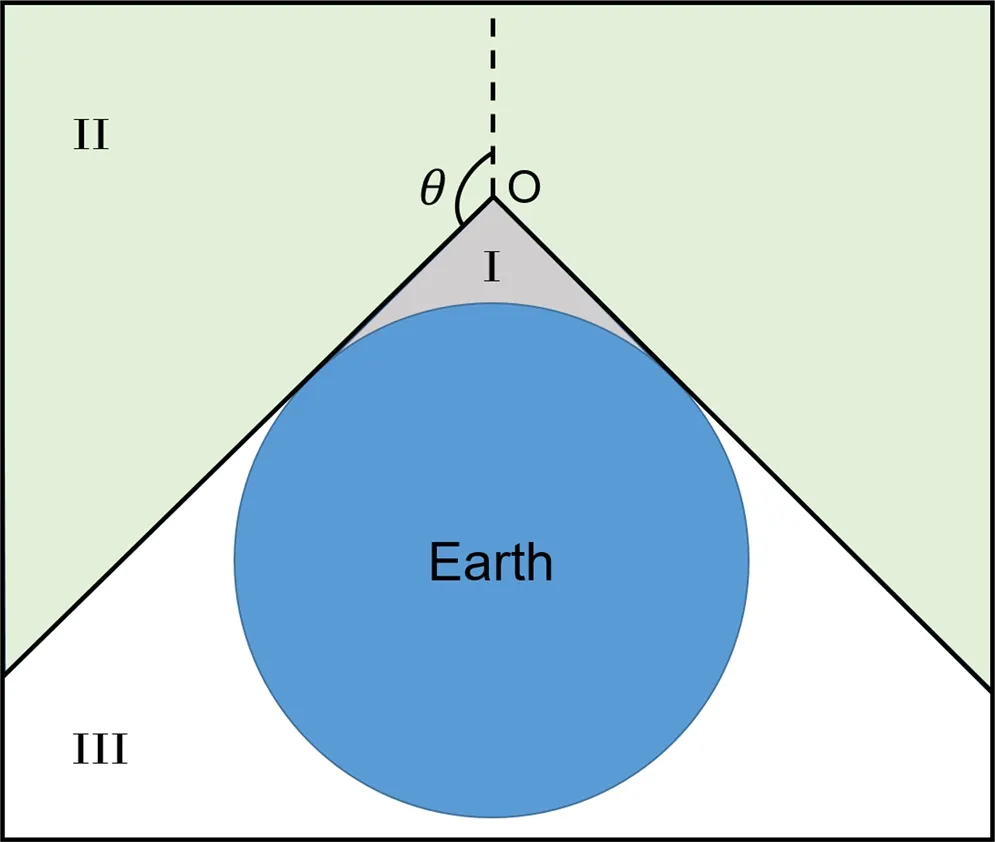
Figure 1. The influence of the Earth’s shielding effect on the angular distribution of particles.

Figure 2. The flux of albedo photons varies with zenith angle (Petry 2005).

However, there are a variety of high-energy particles in interstellar space surrounding the Earth. Satellites around the Earth will inevitably be bombarded by a huge quantity of orbital background energetic particles. The effect of orbital background on observations is an issue that must be considered for space detectors. HXI’s LaBr3scintillator detector is predicted to generate signals by interacting with various energetic particles on orbit. These background particle signals will be intermingled with the beneficial signals of solar X-rays and will interfere with our observations, making accurate hard X-ray imaging of solar flares impossible. In severe circumstances, there are too many background particles, and the resulting background spectrum may totally submerge the Sun’s X-ray observation spectrum, rendering HXI unable to do routine observations. Moreover, each HXI sub-detector crystal is accompanied by a radioactive source for on-orbit calibration,and we must verify that the radioactive source’s full-energy peak is not covered by the background spectrum. As a result,we must analyze and study the background particles in HXI’s orbital space to understand their composition, distribution, and spectral characteristics on the detector,determine the activity of the on-orbit calibration source, and reduce the influence of the orbital background on actual observations as much as possible,thereby improving HXI’s observation capability. Furthermore,analyzing the behavior of the on-orbit background assists us in developing an on-orbit observation plan. Therefore, the estimate of background intensity and distribution is required prior to the launch of the HXI.

The ASO-S will be launched into a Sun-synchronous orbit.This orbit’s altitude will be approximately 720 km above the ground.The orbit is inclined by 98°.The satellite will be in low Earth orbit(LEO)and will travel across the polar regions.As a result, photons, protons, electrons, positrons, neutrons, and αions are among the background particles to be examined.In this research, we investigate these background particles and obtain their spectra and spatial distribution using several models and up-to-date observational data. GEometry ANd Tracking(Geant4, Allison et al. 2006) simulates the detector’s response to these particle fluxes.Finally,we deal with the simulated data and analyze them to reach our conclusion.

2. Background Particles in the Space Environment of HXI

To estimate the on-orbit background, it is crucial to first understand what creates the background. The background is caused by the detector’s interaction with high-energy particles in the environment surrounding the orbit. As a result, to determine which particles exist around the orbit, we must first comprehend the satellite’s space environment.

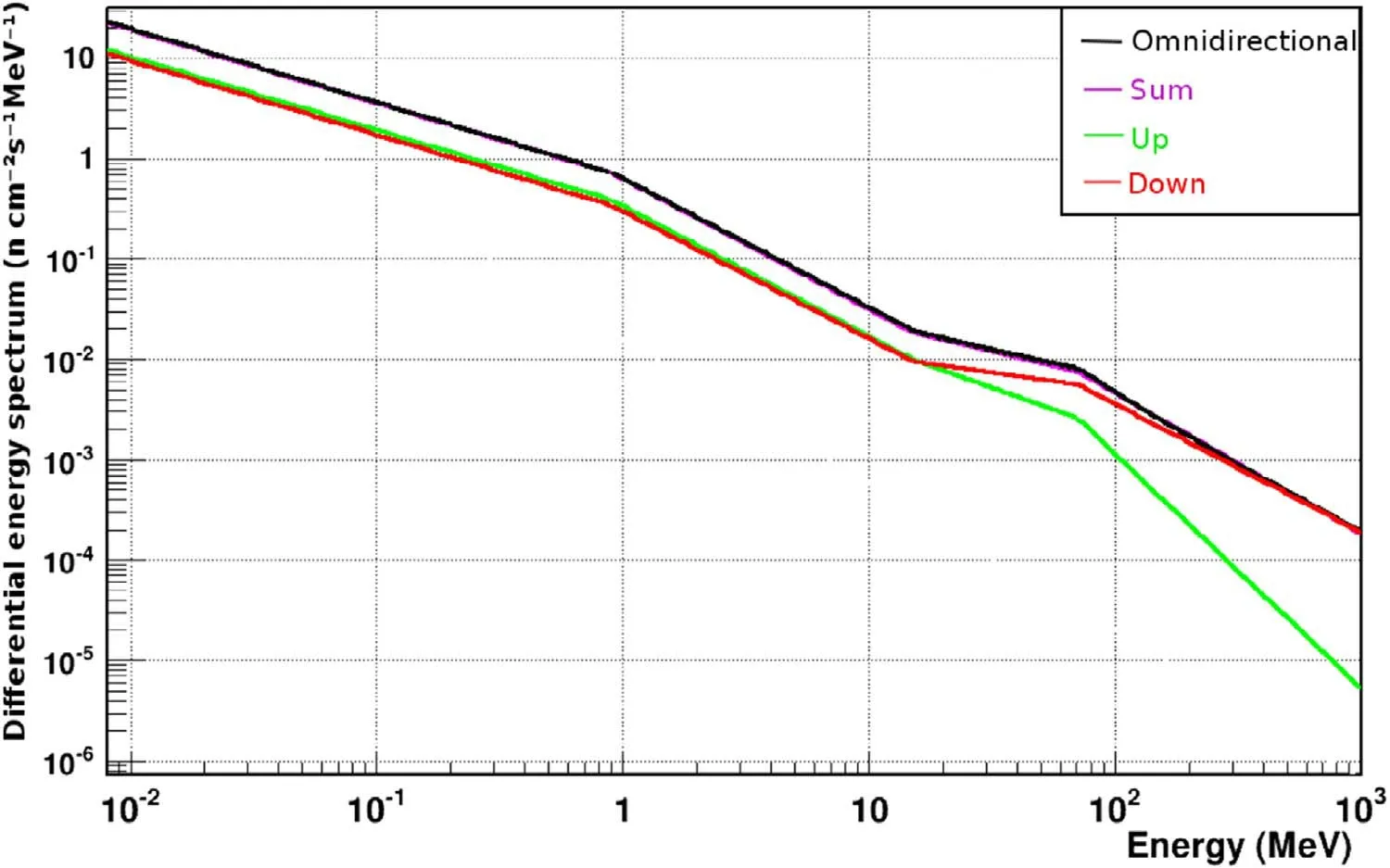
Figure 3.The spectral comparison of the upward(green)and downward component(red)of albedo neutrons for an altitude of 32 km,magnetic latitude of 62°and a solar minimum (Kole et al. 2015).

There are numerous different particles all around the Earth.It is difficult and pointless to consider all of the particles. The deposition of energy by electromagnetic interaction between energetic particles and crystal elements is the primary method by which particles can be detected by detectors. The effect of low-flux particles on the background may be neglected; we only need to study the primary components of the background particles: photons, protons, electrons, positrons, neutrons, and α-ions.

Particles are classified into three types based on their origin:primary particles, secondary particles, and special region particles. The primary particles originate predominantly in interstellar space, beyond the solar system. When primary charged particles reach the Earth, their energy spectra are influenced by solar activity and the geomagnetic field. The interaction between primary energetic particles and the Earth’s atmosphere produces secondary particles. The Van Allen radiation belt is a special region. Solar wind particles trapped by the geomagnetic field are the primary source of Van Allen belt particles.

2.1. The Angular Distribution

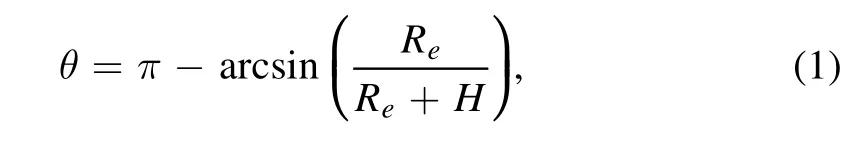
Table 1 Parameters of Different Primary Charged Particles in Equation (4)

The following considerations can be made for particle angular distribution depending on their origin and whether or not they are charged.As seen in Figure 1,the zenith angle is θ when the satellite is at point O. We have the following where Reis the radius of the Earth and equals 6378 km,and H is the satellite’s altitude and equals 720 km. We can get θ ≈116°. Because particles cannot reach the satellite in the white area III due to the Earth’s shielding effect,we assume the particle flux from this area is 0.In terms of the light green area II,the angular distribution for primary particles is uniform.For the sake of simplicity, the east–west influence is ignored.

The angular distribution of albedo photons in the gray region I is relatively complex. The angular distribution of albedo photons at an altitude of 450 km is plotted in Figure 2,and the flux of albedo photons near the horizon that can be found is the largest. The variation of the albedo photon flux with zenith angle in the figure can be simply fitted with an exponential function. The hollow circles in the figure are the SAS-2 data and the solid circles are the EGRET data. The zenith angle of the horizon in the figure is 111°,and the orbital height of ASOS corresponds to the zenith angle of the horizon of 116°. We assume that for ASO-S, the albedo photon flux above the horizon is 0, and the flux is considered constant above 155°,while 116°–155° has a flux variation similar to that of the corresponding region in the figure, so we get:FSecPho∝e-3.424θ.

As to albedo neutrons, they have different angular distributions in different energy bands due to their different production mechanisms. As depicted in Figure 3, the upward and downward components have the same spectra below about 15 MeV, which means the angular distribution of albedo neutrons is isotropic in this energy range. Above 15 MeV, the flux of the downward component gradually exceeds that of the upward component. For ASO-S, we only need to consider the upward component of albedo neutrons. That is, only neutrons from the region I are to be considered.We can also assume that the angular distribution of albedo neutrons in region I is uniform.

Because of their low energy,secondary charged particles and special region particles can be regarded as restricted by the geomagnetic field and presumed to be isotropic.

2.2. The Energy Distribution

The energy spectra of the major particles are discussed in this section. These particles must be considered independently due to their diverse sources and whether they are charged or not.

2.2.1. Primary Particle Spectra

The primary particles are classified as charged particles or neutral particles. A cosmic diffuse photon, also known as cosmic X-ray background (CXB), is the primary neutral particle. It is unaffected by solar activity or the geomagnetic field.When CXB reaches different locations near the Earth,it is believed to be isotropic and to have the same spectrum. As a result, the situation of CXB is quite straightforward. Different satellites can provide CXB spectral data(Gendreau et al.1995;Gruber et al.1999;Watanabe et al.1999;Churazov et al.2007;Ajello et al. 2008). A double power law (PL) of the form expressed below can be fitted to the CXB spectrum below 890 keV

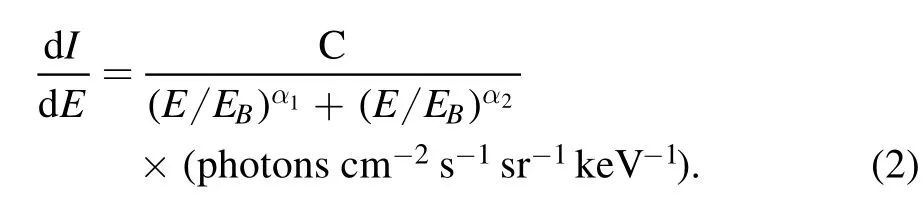
Here C=(10.15±0.80)×10-2, α1=1.32±0.018, α2=2.88±0.015, and EB=29.99±1.1 keV. The fitting parameters are saved in Geant4, and we can use that spectrum directly with the built-in functions of the Geant4 General Particle Source (GPS) module.

When E ＞890 keV, we use the Fermi-LAT (Atwood et al.2009) results and extrapolate to lower energies from E ＞100 MeV

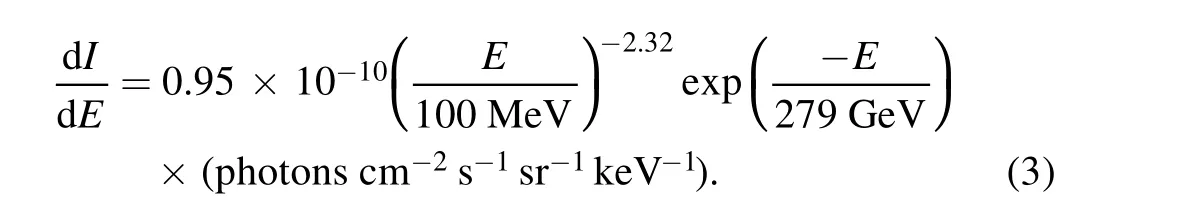
For primary photons,the energy interval in our simulation is 1 keV to 100 GeV, covering the HXI detection energy range.

The spectra of primary charged particles can be assumed to be PLs before they enter the solar system. The modulations of the solar activity and geomagnetic field are used as parameters in the function,and the spectrum of a primary charged particle is described as a PL with modulation parameters(Mizuno et al.2004)

Here R and Ekare the rigidity and kinetic energy of the particles,respectively, e is the magnitude of electron charge,Z is the atomic number of particles,M is the particle mass,and c is the speed of light. Parameter φ represents the solar modulation, which ranges from 500 to 1100 MV. In our simulation,we assume it to be an average value:800 MV.Rcutis the geomagnetic cutoff rigidity and is expressed as(Zombeck 2006)

Here h=720 km is our satellite orbit altitude,REarth=6379 km is the Earth’s radius, and θMis the geomagnetic latitude in radians.

Given the geomagnetic modulation, the flux of low-energy primary charged particles in the orbit of ASO-S will be extremely low. Although primary particles with energies of hundreds of GeV and above have high energy and cannot be stopped by the geomagnetic field,their flux is relatively low.In the meantime, because high-energy particle simulation effectiveness is quite low, only charged particles with energies ranging from 10 MeV to 200 GeV are considered in the simulation.

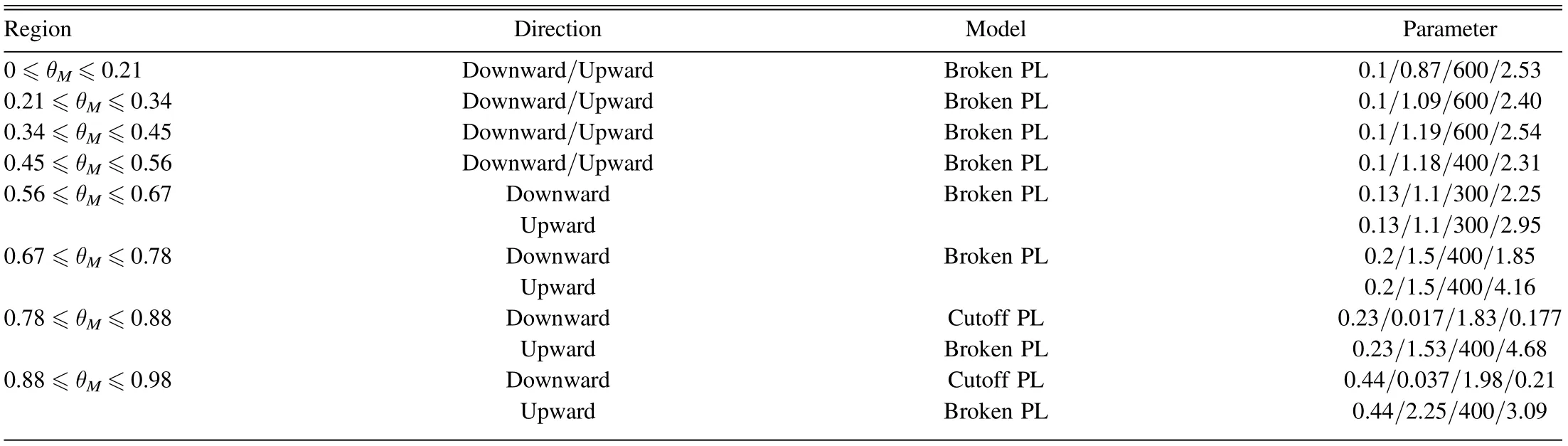
Table 2 Model Parameters for Secondary Proton Flux at the Altitude of HXI

Table 3 Model Parameters for Secondary e-/e+ Flux at the Altitude of HXI

Note.F0/a for the PL model(Equation(15)),F0/a/Ebk(GeV)/b for the broken PL model (Equation (13)) and F0/a/F1/b/Ec(GeV) for the PL plus hump model (Equation (16)). F0and F1are given in counts s-1m-2sr-1MeV-1.

2.2.2. Secondary Particle Spectra

The interaction between primary particles and atmospheric molecules produces secondary cosmic rays. Their fluxes are determined by the primary particles, implying that the flux of secondary components is influenced by the geomagnetic field.

Secondary neutral particles include albedo photons and neutrons. The vertically upward spectrum of an albedo photon at the geomagnetic cutoff rigidity Rcut～4.5 GV can be fitted with a three-piece PL (counts s-1m-2sr-1MeV-1)(Mizuno et al. 2004; Abdo et al. 2009), and extrapolating to 10 keV

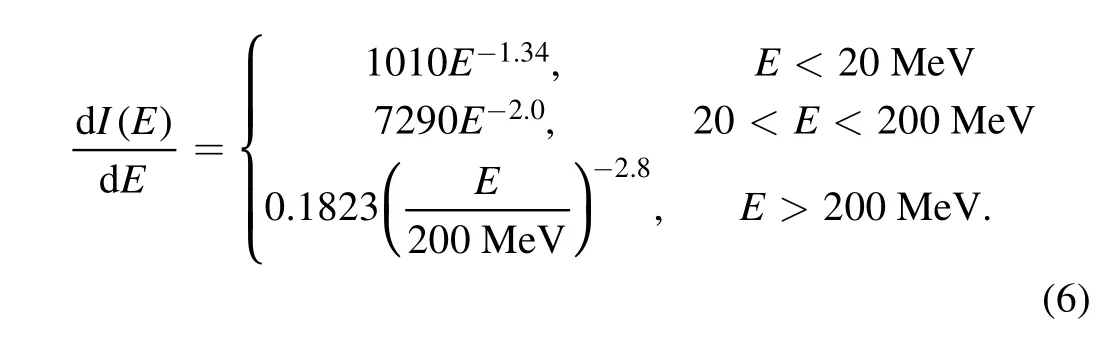
The relationship between the albedo photon flux at different geomagnetic latitudes and the geomagnetic cutoff rigidity Rcut

The spectrum of albedo neutrons at 0 g cm-2atmospheric depth and 42° geomagnetic latitude from Lingenfelter (1963),scaled to the Kole et al.(2015)results,was used to describe the spectrum between 0.01 eV and 8 keV and can be expressed as:

when 0.01 eV ＜E ＜0.1 eV:

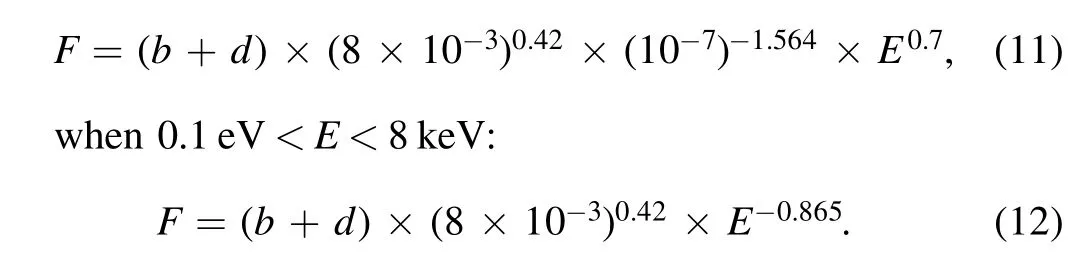
For albedo neutrons,the energy range we consider is 0.01 eV to 30 GeV.

Secondary charged particles include secondary proton and e-/e+. Vertical upward and downward flux spectra of proton,electron,and positron are obtained via the AMS(Alcaraz et al.2000b, 2000c). The data below 10 GeV are derived from the secondary components,and the spectra at various geomagnetic latitudes can be fitted by a broken PL model

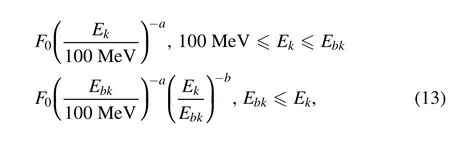
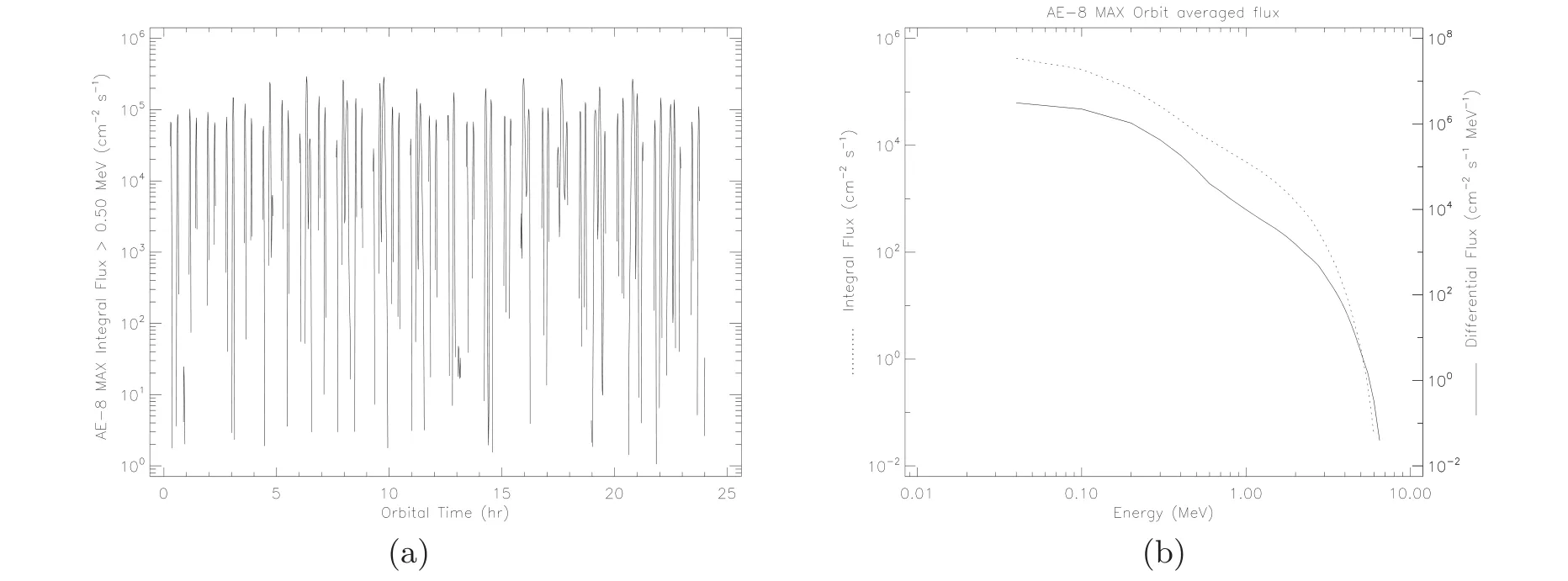
Figure 5. (a) The variation of the trapped electrons’ flux above 0.5 MeV with orbit. (b) The averaged trapped electrons’ energy spectrum for the orbit of ASO-S.

The spectra of secondary charged particles depend solely on the geomagnetic cutoff, as Equation (5) demonstrated, which varies more with the inclination than with the altitude(Cumani et al.2019).The altitude of AMS is 380 km and the altitude of HXI is 720 km. We can obtain their geomagnetic cutoff rigidities at different geomagnetic latitudes. In adopting the AMS models (Mizuno et al. 2004), we select the appropriate secondary charged particle spectral model based on the geomagnetic cutoff rigidity of the HXI. Therefore, the last model parameters for HXI are listed in Tables 2 and 3.

2.3. Special Area

ASO-S will traverse the Van Allen radiation belt, which consists of the outer electron and inner proton belts,in an LEO of 720 km.The particles in the radiation belt come mainly from the solar wind, which is trapped by the Earth’s magnetic field.When the satellite crosses two poles, it crosses the outer radiation belt. The South Atlantic Anomaly (SAA) is also a component of the inner radiation belt. The satellite will also cross this region. The particle fluxes at these two locations are extremely high and distinct from others. Therefore, we should consider them separately and independently.

2.3.1. The Outer Electron Belt

Electrons, which have extremely enormous fluxes, are the principal particles in the outer radiation belt. These electrons have an energy of several MeV. To acquire the electron flux distribution and energy spectrum in the radiation belt at the ASO-S altitude, we register at the website3http://www.spenvis.oma.be/and enter the detector information to obtain relevant data. SPENVIS is the European Space Agency’s space environment information system, a website that provides access to models of the space environment and its consequences. On this website, we utilize the AE-8 model to simulate the radiation belt and calculate electron flux and trapped electron flux that change over time.As shown in Figure 4, the position distribution of electrons is dependent on their energy; the higher the energy, the smaller the distribution area. When ASO-S operates on orbit, the change of trapped electron flux with time can be obtained, as shown in the left of Figure 5,which reflects that the satellite is constantly passing in and out of the radiation belt. The right panel of Figure 5 displays the average energy spectrum of trapped electrons detected by the satellite on orbit for one day;but this spectrum can only be used as a reference. Because the average energy spectrum in Figure 5 is obtained from the statistics of all regions in orbit, the distribution regions of electrons with different energy are different, so we need to consider the electrons with different energy segments separately to get their respective distribution. For electrons in the radiation belt, the energy range we consider is 40 keV to 6 MeV.

2.3.2. The South Atlantic Anomaly (SAA)

SAA is a region with high proton flux. When the satellite passes through this region, the detector will not work, but energetic protons will activate the satellite’s materials. During the activation,high-energy protons interact with material nuclei to produce free neutrons, which then interact with material nuclei and are captured by the atomic nuclei. The nuclei of materials are activated to form radioisotopes,which then decay to produce secondary particles. As a result, the generation period of secondary particles is determined by the half-life of the relevant radioisotopes.The activated elements will continue to contribute to the delayed background after the satellite passes SAA.

The proton flux and other pertinent statistics in SAA can also be retrieved using the AP-8 model from the SPENVIS website.Here we have also revealed the average spectrum of trapped protons and the position distribution of trapped protons with energy above 10 MeV and 100 MeV, and their flux orbital variation and the average spectrum in Figure 6. In our simulation, the energy range of trapped protons is 10–400 MeV.

Figure 6. The distribution of proton fluxes above 10 MeV (a) and 100 MeV (b) at 720 km from the ground. (c) The variation of the trapped protons’ flux above 10 MeV with orbit. (d) The averaged proton energy spectrum for the orbit of ASO-S.

3. Mass Modeling and Simulation Description

The Geant4 simulation toolkit was used to continue the research on HXI’s on-orbit background. To obtain more realistic findings, a comprehensive satellite mass model must be built, as well as a more realistic space particle energy spectrum and angular distribution.Following that,the information received for each particle’s energy spectrum and angular distribution is entered into Geant4 as input data. The background is obtained by processing the simulation’s data.

3.1. Mass Modeling in the Geant4

The model of the entire satellite comprises detailed information such as the size,materials,and relative placements of the detector’s components. The aim is to make the satellite structure as authentic as feasible. To accomplish this, we first convert the complete satellite’s frame engineering drawings to STL file format, then import these STL files into Geant4 using CADMesh. Figure 7 depicts the final mass model of the complete satellite.

HXI is the finest component of the entire model; its collimator parts,spectrometer parts,and electronic components are all meticulously built. The materials used for the various components are as near to the real thing as feasible.Furthermore,there is a difficulty to be noticed in the modeling,which is that the modeling utilizing CADmesh may not be suited for very fine or crucial devices due to its model-building process. As a result, when creating grids and crystals, we use the direct manual method.

There is no need to be overly accurate in construction for the other parts of the satellite, such as the other two payloads LST and FMG,solar panel,service module,and other miscellaneous devices; only the overall mass structure and location distribution are required.

3.2. Simulation Description

To finish the simulation, we will need a mass model, input particle types, energies, positions, angular distributions, the necessary physical processes, and the acquisition of pertinent information supplied by the simulation.

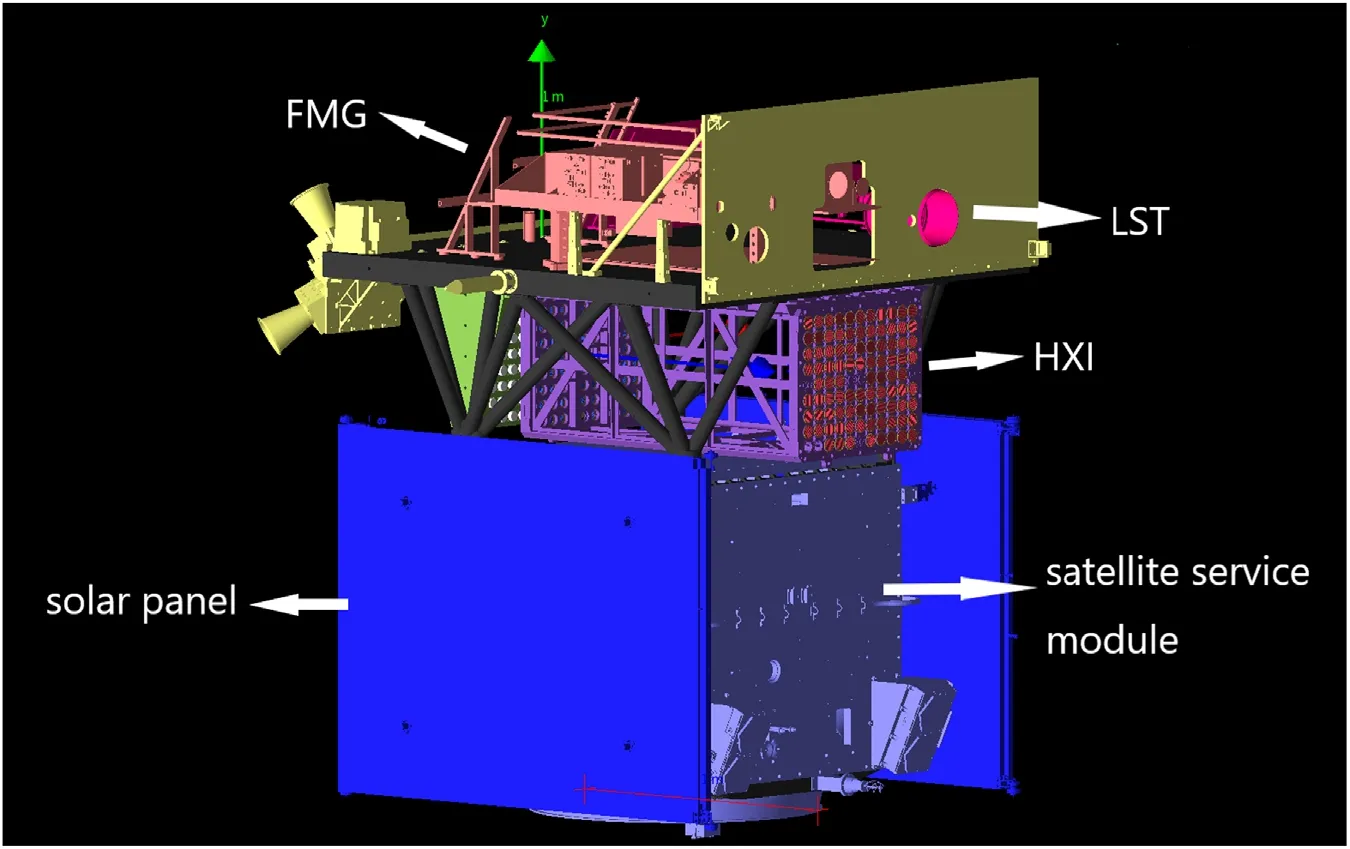
Figure 7. The mass model of ASO-S in Geant4.

Figure 8. The background (energy range: 10 ～600 keV) of one-day on-orbit changes with time.

To simulate isotropic emission, first, finish the ASO-S mass model. Then, a spherical surface around the model is used as the emitting surface, and particles are emitted into a sphere with a uniform angular distribution. The type and energy distribution of the released particles are similar to those detailed in the preceding sections. The previously indicated simulation of the Earth’s blocking effect can be completed by modifying the partial biasing of the spherical emission surface. The input particles in this simulation are mostly electrons, positrons, photons, neutrons, protons, and alpha particles. Electromagnetic interaction, hadronic interaction, and radioactive decay will be considered as physical processes. As a result, to finish the simulation, the appropriate physical list must be matched in the simulation.In the simulation, we use the QGSP_BIC_HP_LIV physical list, which can adequately cover the physical process of the required energy range. Moreover, we added the G4RadioactiveDecay process to the physical list to simulate the secondary particles produced by radioactive isotope decay induced by nuclear reactions. The cutoff length (the range threshold for secondary particle generation) was set to 10 μm. Finally, the energy deposition created by each incident particle is gathered in the HXI crystal of LaBr3.

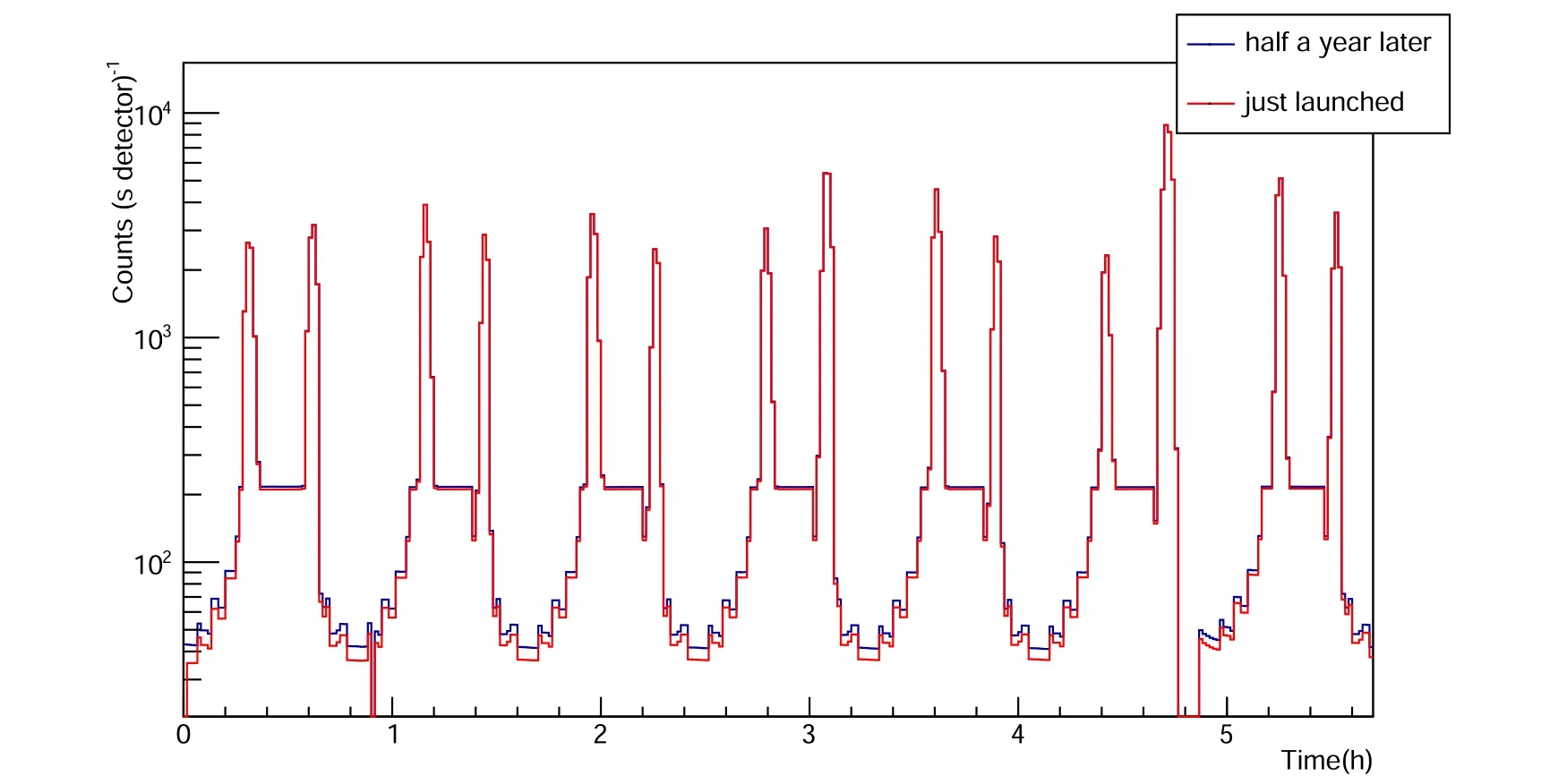
Figure 9. The background (energy range: 10 ～600 keV) changes with time, the blue line is half a year after launch, and the red line is just launched.

Figure 10. The average decay curve for different isotopes and mean lifetimes and proportions of their principal components.

As a result, after obtaining the deposited energy, Gaussian sampling must be performed by the energy resolution to match the true recorded energy.

Each particle’s simulation process is treated as an event in Geant4.Every event is made up of several steps.The particle’s track is made up of these steps. Every step comprises information about the particle’s energy deposition, position,and time of emission. We can determine whether each particle generates an instantaneous background or a delayed background and delay time based on this time.

4. Results and Analysis

Figure 11. The simulated average background spectrum and some main components outside the radiation belt after half a year of on-orbit operation.

We can characterize how background counts vary over time by studying simulation data.Figure 8 depicts the time-variation of background flux in one day on orbit. The figure has several sharp peaks, indicating that the detector has entered the radiation belt. The electrons in the radiation belt rapidly increase the background flux.Outside of the radiation belt,the typical tendency of the background flux grows approximately sevenfold as the orbital geomagnetic latitude increases. The background flux in the radiation belt is one to two orders of magnitude more than the background flux outside the radiation belt.The time interval with zero flux shows that the satellite has entered the SAA zone,at which period the detector is turned off and no longer records data.

The background after the satellite has just been launched differs from that half a year afterward (Figure 9). Their trends are similar, but the satellite’s orbital background after half a year on orbit is nearly 10 cts s-1greater than when it is first launched. The contribution of the sustained decay of radioisotopes created by energetic hadron-activated materials is responsible for the rise in flux. The high-energy protons in the background will cause materials to be activated, and the halflives of some activated materials are short, while others are long. The average decay curves obtained for different isotopes are shown in Figure 10. The dominant isotopes are11C and24Na,which come from the interaction of protons with a carbon fiber framework and aluminum alloy materials, respectively.The detector’s background counts will constantly be impacted by the decay of long-lived isotopes, such as22Na and7Be.

Figure 11 shows the simulated average background spectrum outside the radiation belt after half a year of operation, as wellas the contributions of several main components. At the right end of the spectrum, the 511 keV emission line can be seen,which typically results from the annihilation of a positron and electron. High-energy protons and α-particles interact with the materials to create radioactive isotopes, which then decay to produce positrons via β+decay. The annihilation of positrons and electrons results in the production of two 511 keV photons.The other is detected when one photon escapes, resulting in 511 keV emission lines. In addition, an unusual elevation appears on the left low-energy side of the spectrum, which is primarily caused by primary protons and alpha particles. This could be due to the accumulation of secondary low-energy particles following the interaction of high-energy particles with the instrument. Outside the radiation belt, the average background spectrum is dominated by primary protons.

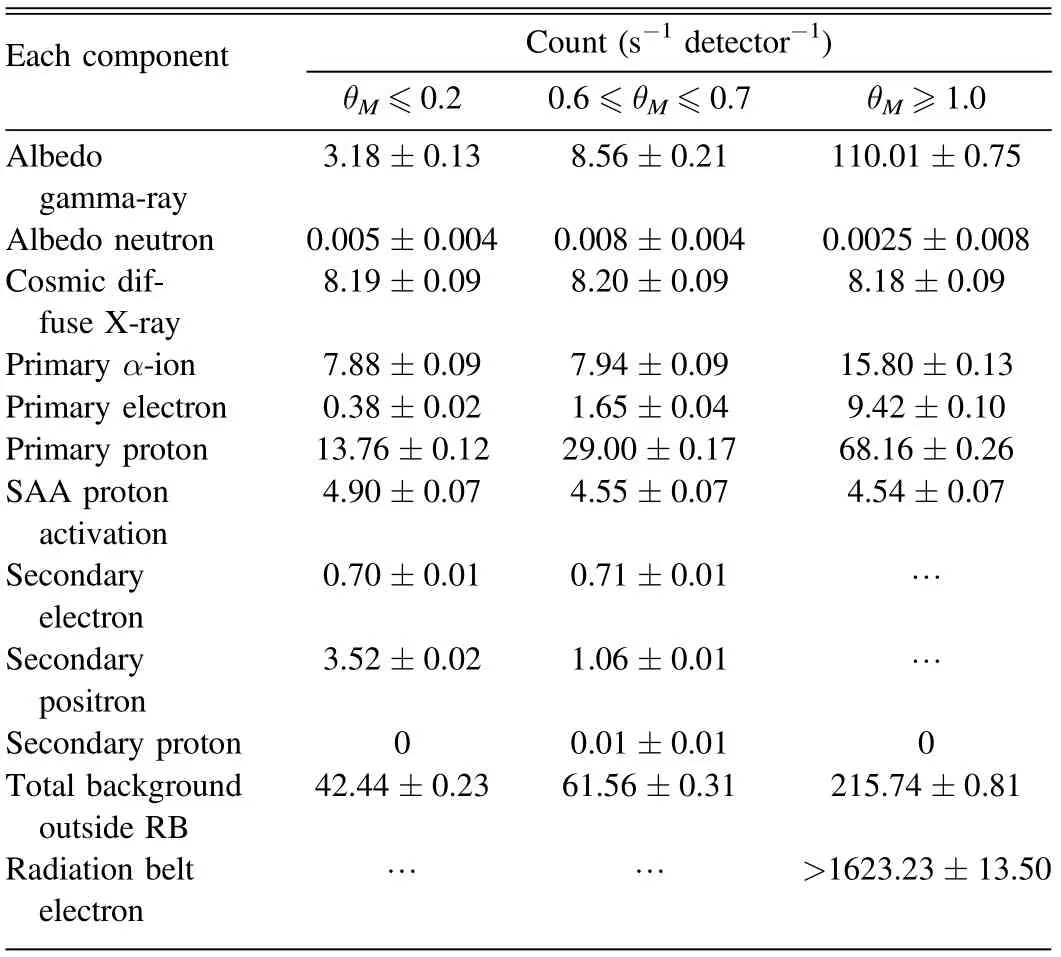
Table 4 The Contribution of Different Components to the Background at Different Geomagnetic Latitudes (energy range: 10 ～600 keV)

The counts of the different components in this energy interval (10 ～600 keV) are reported in Table 4. The radiation belt electrons are undeniably the main source of background in the radiation belt.This produces a background count that is one or two orders of magnitude greater than the other components.Outside the radiation belt, primary protons are the main component of the background at low geomagnetic latitudes,while albedo photons are the main component at high geomagnetic latitudes (θM＞1.0).

Because of the modulation of the geomagnetic field on orbital environmental particles, the background flux and spectrum differ at different geomagnetic latitudes.We comparethe background spectra of different geomagnetic latitudes with the count spectra of four GOES soft X-ray (SXR) flares (Su et al. 2019). The spectra and relevant information on SXR flares are revealed in Figure 12 and Table 5.The comparison of background and flare counting spectra is shown in Figure 13.Outside of the radiation belt, the background energy spectrum has a similar structure,and the higher the geomagnetic latitude,the larger the background counts. The background flux is greatly increased inside the radiation belt, submerging the majority of the flare energy spectrum at the high energy end.Taking the M2-class flare as an example, its spectrum is covered by the background spectrum of geomagnetic latitude greater than 1 rad above about 90 keV, by the background spectrum of geomagnetic latitude greater than 0.6 rad above about 120 keV,and by the background spectrum of all latitudes above about 140 keV.

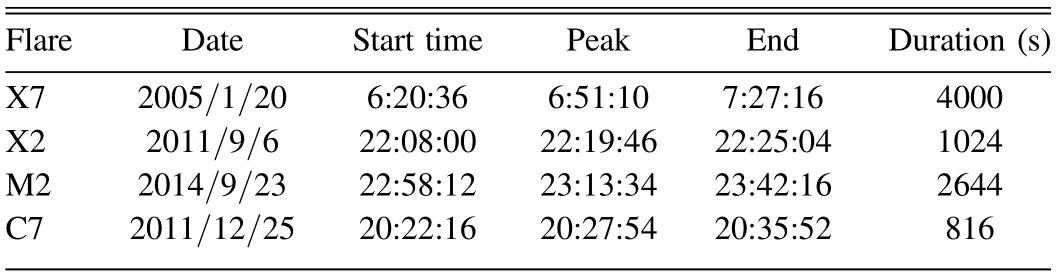
Table 5 The Information on four SXR Flares

In addition, for the self-calibrated sources employed in the detector, the energy peaks required for calibration must be visible in the orbital background while not interfering too much with the energy spectrum observation of the flare.We presently employ the 36 keV peak of the LaBr3internal background and the 59.5 keV peak of the calibration source241Am as calibration energy peaks. The internal background of the LaBr3crystal is from its internal contamination of138La impurities. The decay of138La can produce 36 keV characteristic X-ray. Because the internal background’s mono-energy peak is quite faint and may not be used for calibration at high geomagnetic latitudes, we choose a calibration source with sufficient activity to address this issue. The mono-energy peak of the calibration source is powerful enough to be visible beyond the radiation belt orbital background and is sufficient for calibration,as illustrated by the green curve in Figure 13.In general, the best time to calibrate the satellite is when it is at low geomagnetic latitudes and no large flares are present.

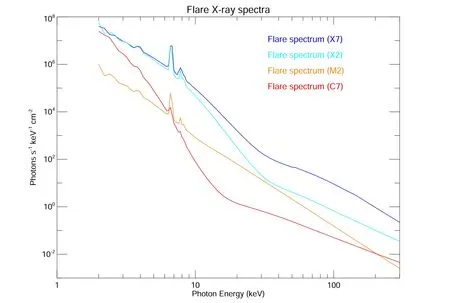
Figure 12. The spectra of four SXR flares at the X7, X2, M2 and C7 GOES classes.

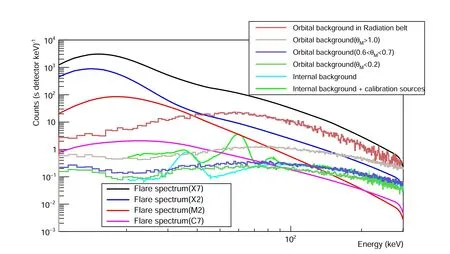
Figure 13.Simulated background spectra at various geomagnetic latitudes(θM),internal background and calibration sources of the detector,and count spectra for four flares at the X7, X2, M2, and C7 GOES classes.

The observed flare count spectrum is obtained after subtracting the background, so the statistical error of the final flare count spectrum involves the statistical errors of the flare and the background. To simulate the observed flare count spectra, we can add the flare count spectra to the background spectra, and then subtract the background spectra to get the final observed flare count spectra. In order to perform a statistical analysis of the final flare count spectrum,we need to determine the statistical duration of the flare and the background. The spectra of the flares are all from the average spectra of 10 s before the flux peak time point of the flares.Likewise, the background spectrum statistics are for 10 s. The final flare count spectra with statistical errors are shown in Figure 14. From the figure, it can be found that the energy ranges with large errors for all flares are mainly concentrated at the high energy end. At the same energy, the statistical errors are relatively larger for flares of lower class, and they are relatively larger in the high geomagnetic latitudes, while the statistical errors are largest in the radiation belts. As for the C7-class flare, its errors are relatively large in the full-energy band of the radiation belt region and the high-energy end of the non-radiation belt region, and the large errors mean that the background subtraction accuracy will significantly affect its energy spectrum observation. In the low-energy band outside the radiation belt, a C7-class flare has relatively small errors,and the detectors still have a certain detection capability for it.

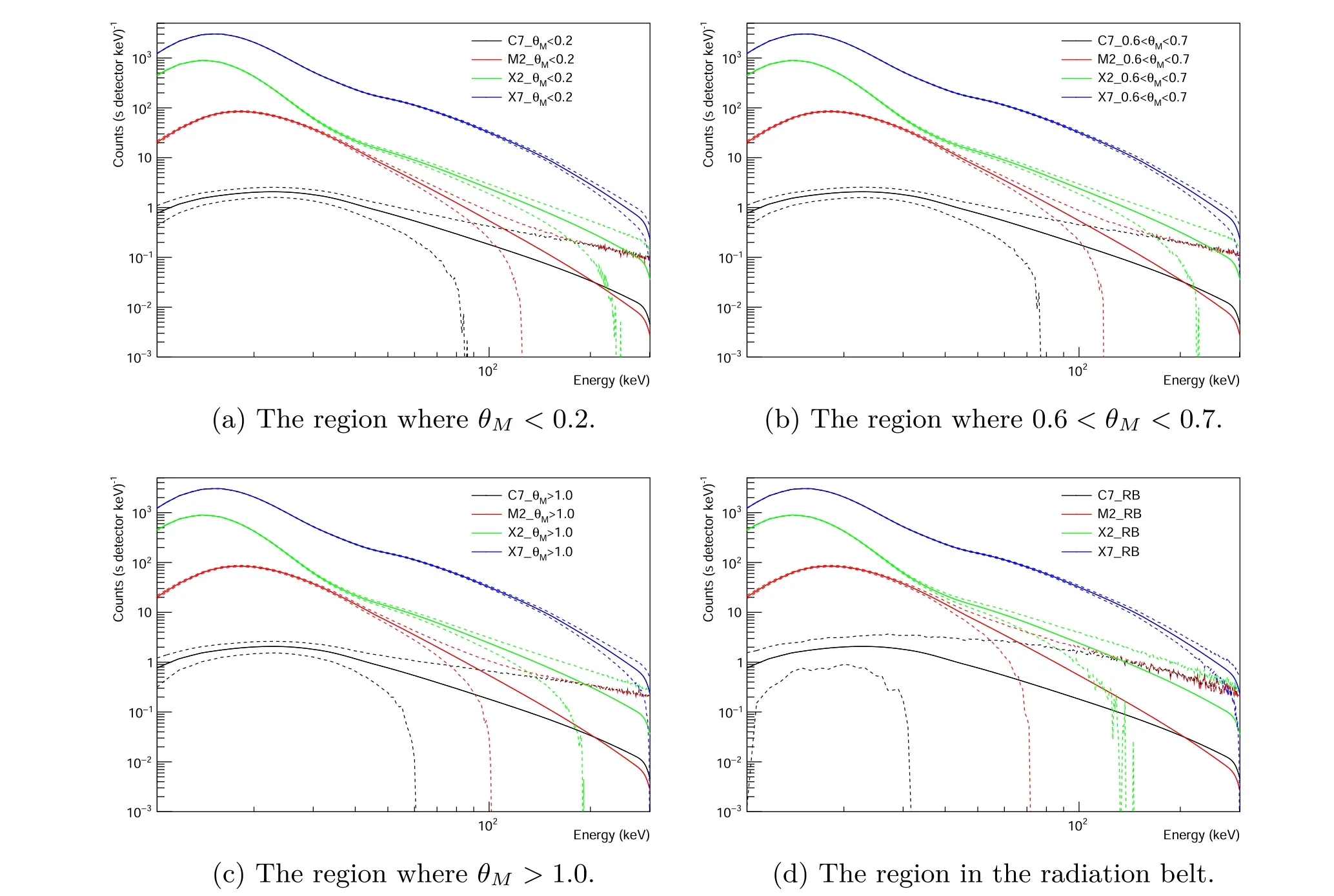
Figure 14.Comparison of the final flare count spectra with one standard deviation at different orbital regions.θM is the geomagnetic latitude.The dashed lines above and below the solid line of the same color indicate the upper and lower boundaries of the 1σ error of the corresponding flare spectrum.The spectra here are based on a fully open detector module (no grid blocking in front of the LaBr3 detector).

The count spectra of flares in Figure 13 are measured by the detector module that records the flux of a flare. In contrast,for the detector module measuring the modulation signal, the maximum photon count of the measured flare X-rays is only half that of the detector module monitoring the flux (because the maximum transmittance of the sub-collimator is 0.5),while the background spectrum does not change significantly. The different flare count spectra with one standard deviation at different transmittance are compared in Figure 15. The accuracy of photon count determines the accuracy of the modulated signal. When the transmittance is relatively small,say 1/4 or smaller, the statistical errors of C-class and lower flares are very large on the full energy band, which indicates that the photon counting accuracy of these flares is relatively poor, leading to poor modulation signal accuracy and ultimately making the flare imaging have quality poor. For the flares above C-class,the imaging quality in the energy band above 50 keV is inversely proportional to the energy.

From Figure 13, we can find that the peaks of the count spectra of the flare appear around 20 keV, while the peak of the background spectra appears at 80–90 keV. From Figure 12, we have found that the lower the flare X-ray energy, the higher the flux. However, the effective blocking of low-energy X-rays by the shield designed for the HXI spectrometer results in the highest counts of the final obtained flare count spectrum occurring around 20 keV.Therefore, 10–50 keV has finally become the energy band with the largest signal-to-noise ratio. We also count the 10 s flare counts before each flare flux peak and the 10 s background counts at 0.6 ＜θM＜0.7 to get the final flare count rates and their statistical errors in different energy bands. The results are displayed in Table 6. Assuming that whether the ratio of the flare count to its error is greater than 3 as a criterion for identifying a flare,X7 and X2 class flares are identified in the full energy band,while M2 and C7 class flares are identified in the energy band below 150 keV.In addition, the energy band of 10–50 keV has the best signal-to-noise ratio and may be able to be used for monitoring flare formation and class.

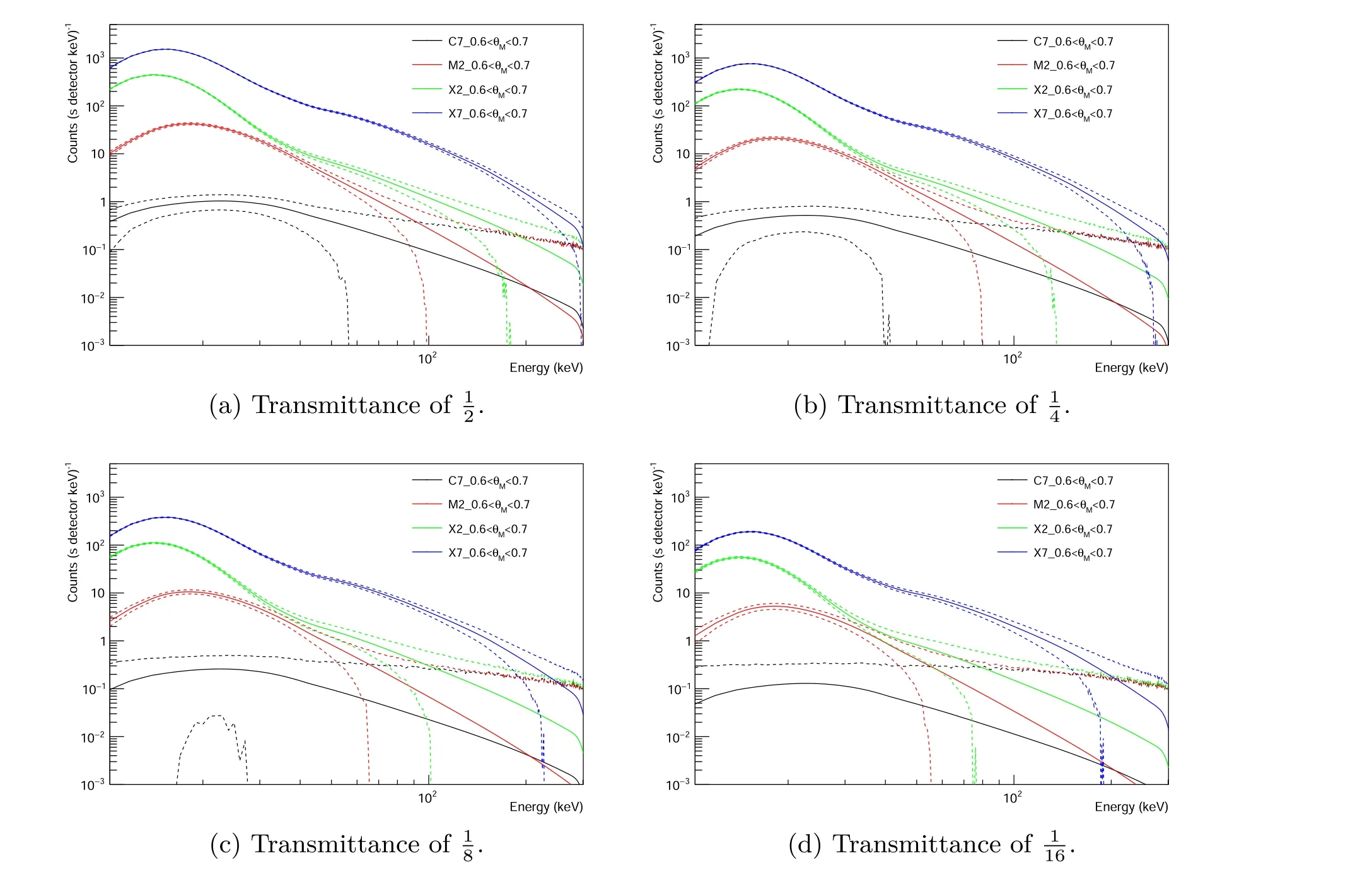
Figure 15. Comparison of the final flare count spectra with one standard deviation of the sub-collimator at different transmittance at 0.6 ＜θM ＜0.7. The lower boundary of 1σ error of the C7-class flare spectrum is not drawn in the figure with the transmittance of 1/16 because the error is too large and beyond the range of the vertical axis.

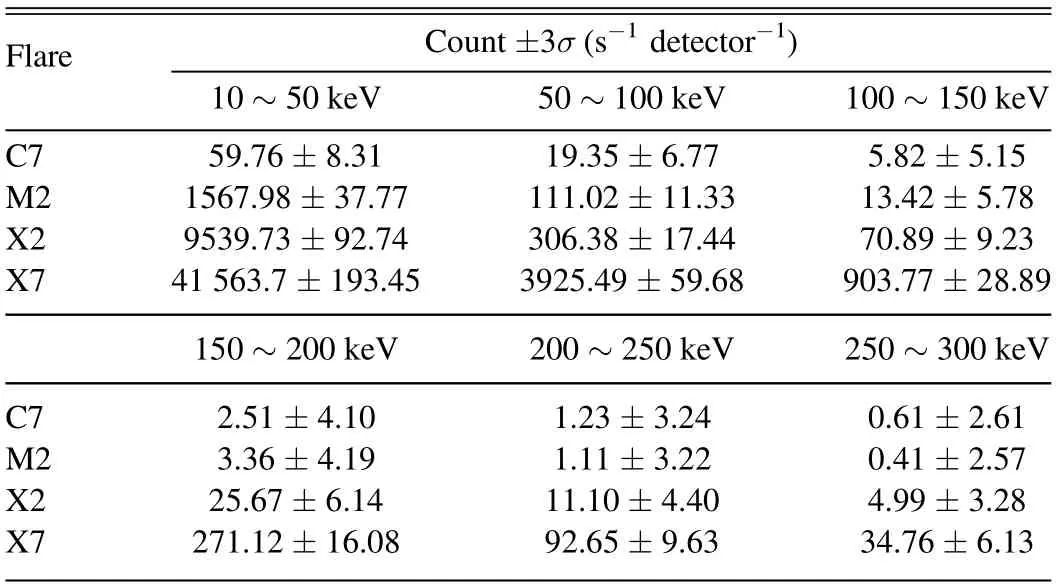
Table 6 The Flare Count Rates Obtained 10 s before the Peak of the Flare Flux and their Standard Deviations (σ) in Different Energy Bands at 0.6 ＜θM ＜0.7

5. Summary

The HXI is one of the instruments onboard ASO-S that will operate in a Sun-synchronous orbit at an average altitude of 720 km. Because it is in LEO, its space background will consist of primary and secondary particles, and because such an orbit is quite close to the polar orbit and will travel through the Van Allen radiation belt in each orbit, the radiation belt’s electrons will likewise add to the satellite’s background.

We established through simulations that radiation belt electrons are the dominant source of background, outweighing the contribution of all particles beyond the radiation belt by one to two orders of magnitude. Outside the radiation belt,the background flux varies up to sevenfold,with primary protons providing the majority of the background at low geomagnetic latitudes and albedo photons providing the majority of the background at high geomagnetic latitudes. Within half a year, the delayed background from material activation provides almost 10 cts s-1to each detector module.

According to the statistical study of the simulated background spectrum and the flare response spectrum, background subtraction accuracy substantially influences the observation of C-class and lower flares in the high-energy band.Furthermore,the comparison research reveals that the best signal-to-noise ratio is found in the 10–50 keV energy region, which may be utilized to monitor flare formation and class.

In this simulation, the environmental particle distribution model is relatively simple. In certain areas, the angular distribution of various particles is simply uniform. The true situation is far more convoluted,as evidenced by the east–west influence of primary charged particles, and so on. However,these simplifications have a limited impact on the average counts and change in the background. We will conduct more extensive analyses in the future to compare how much the results differ.

Acknowledgments

This work is supported by the Strategic Priority Research Program on Space Science,Chinese Academy of Sciences(No.XDA 15 320 104), National Natural Science Foundation of China(NSFC,Grant Nos.11973097,12173100 and 12022302)and the Youth Innovation Promotion Association CAS (Nos.2021317 and Y2021087).

ORCIDiDs

Wei Liu https://orcid.org/0000-0002-1490-5172