Multi-scale Analysis of the Relationships between Solar Activity, CO2 and Global Surface Temperature

Zhen Li, Lijun Chang, Jiahui Lou, Yi Shen, and Haoming Yan

Abstract To reveal whether the dynamics of solar activity precede those of global temperature,especially in terms of global warming, the relationship between total solar irradiance (TSI), which is treated as a proxy of solar activity, and global surface temperature (GST) is investigated in the frequency domain using wavelet coherence. The results suggest that the effect of TSI on GST is mainly reflected on the characteristic scale around 22 yr,and variations in TSI lead to changes in GST with some delay effect as shown by the phase difference arrows. However, this implicated relationship has been perturbed by excessive CO2 emissions since 1960. Through the combination of co-integration analysis and wavelet coherence,the hidden relationship between TSI and GST has been uncovered without the CO2 effect and the results further indicate that TSI has a positive effect on GST at the characteristic scale around 22 yr with a 3 yr lead.

Key words: Sun: activity – planets and satellites: surfaces – Earth

1. Introduction

An increasing trend of about 0°.6 C in the global surface temperature (GST), which is captured in the last 150 yr, has been considered to be the main manifestation of global warming (Souza Echer et al. 2012). Global warming is not only a hot research topic at present but also the most controversial issue (Gil-Alana et al. 2014; Kristoufek 2017; Li et al. 2018). On the one hand, many researchers discuss how the rapid increase of CO2concentration caused by human activities is the main reason for climate warming since the industrial revolution. Foukal et al. (2006) found that the total solar irradiance (TSI) variations extending back about 10,000 yr using10Be are too small to drive global climate variations on centennial, millennial and even million-year timescales. In particular,the commonly accepted point of view represented by the Intergovernmental Panel on Climate Change (IPCC) holds that the CO2greenhouse effect has been the dominant cause of global warming since the middle of the twentieth century. On the other hand, other researchers suggest that the GST rise has resulted from fluctuation in solar energy to a large extent.This fluctuation is an important driving factor affecting the Earth’s climate change. Using the moving average method, Valev(2006) found a significant correlation between GST and the sunspot number (SN) over the period 1856–2002. Given that the analysis result that both solar and temperature data follow the same Lévy walk process, Scafetta & West (2010) not only confirmed the existence of a complex and non-linear link between solar activity and GST, but also obtained further evidence that spectral coherence can be used to represent this link. Scafetta (2014) demonstrates that GST and SN are characterized by a common statistical fractional model,indicating that the two parameters are quite related to each other at multiple timescales. Therefore, it is essential to determine which cyclical components and non-cyclical components (especially the long-term trend in global temperature change)are most influenced by solar activity or CO2emissions.

Controversies in the literature suggest several issues on the relationship between global climate change and solar activity.First, without a suitable physical model, any discussion about the statistical significance of a correlation is not so convincing.Second, pioneering researches show an obvious methodology dependence. The signature of solar or CO2emissions in GST observations can be distinguished by applying specific analysis methods which further consider non-linearity, multi-timescale oscillations and filtering of multiple climate change contributions. Third, the cycle amplitude and phase relationship might change with the increase of time.Hereby,we propose to utilize the wavelet coherence (WTC) to solve the above-mentioned issues.WTC is an advanced signal processing method which is special to study the multi-scale relationships between two nonstationary time series in the time-frequency domain.The rest of the paper is structured as follows. Section 2 describes the data sets used in this study and the basic principles of WLC.Section 3 presents the hidden relationship between TSI and GST after controlling the influence of CO2emissions.Section 4 presents concluding remarks.

2. Data Sets and Methods

2.1. Data Sets

SN and TSI are two important parameters to describe solar activity (Rigozo et al. 2011; Kopp 2016). Compared with the indirect effect of sunspots, TSI is the direct indicator of the solar activity parameter which is responsible for the Earth’s climate change. Limited by unavoidable instrumental errors,the measurable absolute level of TSI ranges from 1360 to 1375 W m-2. The mean value of TSI from 1979 to 2008 has been tuned to 1366.1 W m-2(Soon et al. 2011). Kopp & Lean(2011) suggest a TSI value of 1360.8±0.5 W m-2as the best representation of solar minimum. The impact of this uncertainty in TSI on GST is beyond the scope of this paper.It must be realized that recognizing the uncertainty in TSI is a premise for correctly evaluating the dynamic evolution of the Sun-Earth system.

In view of some misunderstandings and inaccurate information about TSI, further explanation is necessary. Since the direct and continuous satellite observation data of TSI have only been accumulated for about 30 yr,which is insufficient to study the long-term effect of climate change (Zhao &Han 2012; Soon et al. 2014), the TSI before 1979 is constructed using other solar indicators related to TSI. In this paper, we apply the reconstructed TSI data provided by the Laboratory for Atmospheric and Space Physics (LASP)Interactive Solar Irradiance Data Center (LISIRD), which is available at https://lasp.colorado.edu/lisird/.The main reason for choosing the TSI reconstruction from LISIRD is that it uses version 2 of the Naval Research Laboratory’s (NRL) TSI variability model (NRLTSI2) to recover historical TSI from 1610 January to 2020 December.The NRLTSI2 computes TSI from the variations with respect to quiet Sun conditions resulting from bright faculae and dark sunspots on the solar disk, where the magnitude of the irradiance variations is determined by a linear regression of proxy Mg II index sunspot area indices against the approximately decade-long solar irradiance measurements of the Solar Radiation and Climate Experiment(SORCE).Compared with the first version,version 2 improves the data quality of sunspot darkening indices based on new cross calibration of the current sunspot region observations made by the Solar Observing Optical Network(SOON) with the historical records of the Royal Greenwich Observatory (RGO), which severely affects estimates of TSI prior to November 1978 (Coddington et al. 2016).

As for the global surface air temperature,our analysis in this paper is based on Goddard Institute for Space Studies Surface Temperature product version 4 (GISTEMP v4), which is available at https://data.giss.nasa.gov/gistemp/. The GISTEMP v4 integrates version 4 of the Extended Reconstructed Sea Surface Temperature (ERSST) data with land surface air temperature from version 5 of the Global Historical Climatology Network(GHCN)monthly data set to create hybrid surface temperature.Compared with the old version,the newer ERSST version improves the spatiotemporal variability of SST and absolute SST.The new GHCN version provides a much larger number of stations (26000 versus 7200 in version 3)and more comprehensive uncertainties for calculating station and regional temperature trends. Additionally, historical spatial variations in surface temperature anomalies are derived from historical weather station data and ocean data from ships,buoys and other sensors. Data uncertainties will arise with the increase of measurement uncertainty in spatial coverage of the station record, and also of systematic biases due to technology shifts and land cover changes.Previously published uncertainty estimation for GISTEMP included only the effect of incomplete station coverage. The newer version updates this term using currently available spatial distributions of source data,state-of-the-art reanalysis, and incorporates independently derived estimates for ocean data processing, station homogenization and other structural biases.

The resulting 95%uncertainties are near 0.05°C in the global annual mean for the last 50 yr and increase going back further in time reaching 0.15°C in 1880. The GISTEMP provides monthly estimates of GST change in the form of temperature anomalies (deviations from the corresponding 1951–1980 means with a scale of 0.01°C) from 1880 to the present(Lenssen et al.2019).It should be noted that if station histories,which could indicate documented changes in station location,instrumental condition, time of observation, etc., exist, it may be possible to correct the station records affected by those nonclimatic biases.It can be more helpful if parallel measurements associated with the station change are available.Unfortunately,station histories cannot be reached. Therefore, we should recognize that the GST may not be the correct metric to study climate change because the GST record may be contaminated by other non-climatic factors as explained and outlined in Connolly et al. (2021).

2.2. Methodology

The mathematical approaches employed in this research include the continuous wavelet transform (CWT). We use the cross wavelet and the wavelet decomposition to systematically study the effect of carbon dioxide on global temperature from two aspects of period term and long-term trend term respectively.CWT,a time-frequency analytical method,which was characterized by multi-resolution and time-frequency localization,is a good tool to detect cyclical signals.At present it is widely used in time series processing (Torrence &Compo 1998).

where π−1/4is the normalization factor,η is the dimensionless time and w0is the dimensionless frequency, which is set to 6 for a good balance between time and frequency localization.Based on the CWT, the WTC of two time series Xnand Yn(n=1, 2,…, N) is defined as

The wavelet decomposition can effectively decompose a signal into different scale spaces by stretching and translating the wavelet basis function. The orthogonal discrete Meyer wavelet is selected as the wavelet basis function, which can decompose a signal into orthogonal frequency levels. Each level is limited by a power of 2(Souza Echer et al.2009).In the wavelet decomposition analysis, the original signal (S) is decomposed in the approximation (A) and the detail (D). The approximation contains the low-frequency part of a signal,whereas the detail contains the high-frequency part of a signal.After the first level decomposition, it is represented by S=A1+D1.After the second level decomposition,the approximationobtained from the first level decomposition is further decomposed into the approximation and details. Note that the detail obtained from the first level decomposition should not be decomposed again. The second decomposition can be defined as S=A2+D2+D1 and A1=A2+D2.In this sequential way,after the Nth decomposition, the original signal is finally decomposed into: S=AN+DN+...+D2+D1 where D1, D2,…,DN is the detail obtained by decomposition from level 1,level 2 to equal level N,and AN is the detail obtained through the decomposition from level N. The optimal decomposition level is determined based on entropy criterion and the process is repeated until this criterion is reached(Echer et al.2004).In this paper, the WT is performed until the fifth level decomposition with the approximation A5 and the detail D5.The corresponding frequency bands are shown in Table 1.

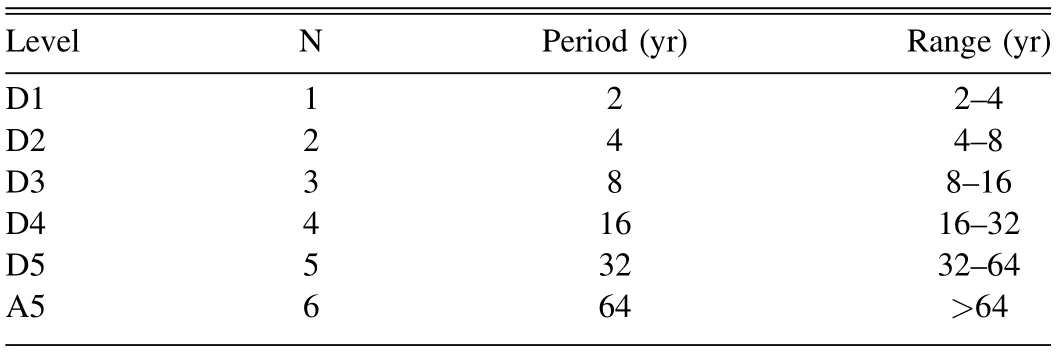
Table 1 Frequencies Corresponding to the Scales of the Meyer Wavelet Function with a 1 yr Sampling Period

3. Results and Discussion

Figure 1 displays the monthly time series of total solar radiation and GST from 1882 to 2020, in the left and right panels respectively.

In Figure 1, we can see that the TSI time series displays a significant periodic fluctuation with varying amplitudes.Meanwhile, the GST change is quite stable up until 1960 when an obvious upward trend begins and keeps up until the end of the analyzed period.This upward trend is usually considered to be related to the excessive emission of carbon dioxide.A detailed discussion on it is given later. Further, Figure 2 presents the CWT results of the TSI time series and the GST time series,in the left and right panels respectively.

In the figure, the yellower the color, the higher the power.The bold contour line separates the insignificant area and significant area that passes the 95% significance test under the null hypothesis of the red noise (i.e., the first-order autoregressive process).The thin solid line of the cone of influence distinguishes the reliable and unreliable regions due to the edge effect by separating the whole time-frequency domain into dark and light colors. It is clear from Figure 2 that (1) for the TSI wavelet power spectrum the high power region with statistical significance is located around the frequency band of 128 months, which is quite stable in time, revealing that TSI has a significant oscillation with an 11 yr period; (2) for the GST wavelet power spectrum, however, some regions with high powers are observed. None of them passed the red noise test.Two potential reasons can explain it:either GST really does not have a significant period, or the significant period is greater than 512 months, which cannot be detected by wavelet analysis. Obviously, this dilemma will be overcome in the future with the increase of observation data; (3) the wavelet power spectra of TSI and GST are not consistent, and TSI and GST have no common significant period in the analyzed range.

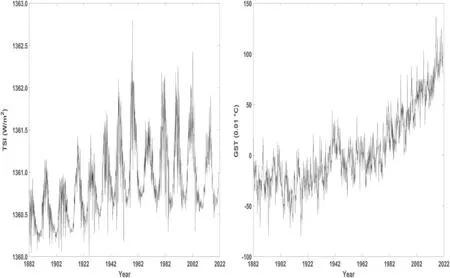
Figure 1. Monthly TSI and monthly GST from 1882 to 2021, in the left and right panels respectively.

Figure 2. Wavelet power spectrum of monthly TSI and monthly GST from 1882 to 2021, in the left and right panels respectively.

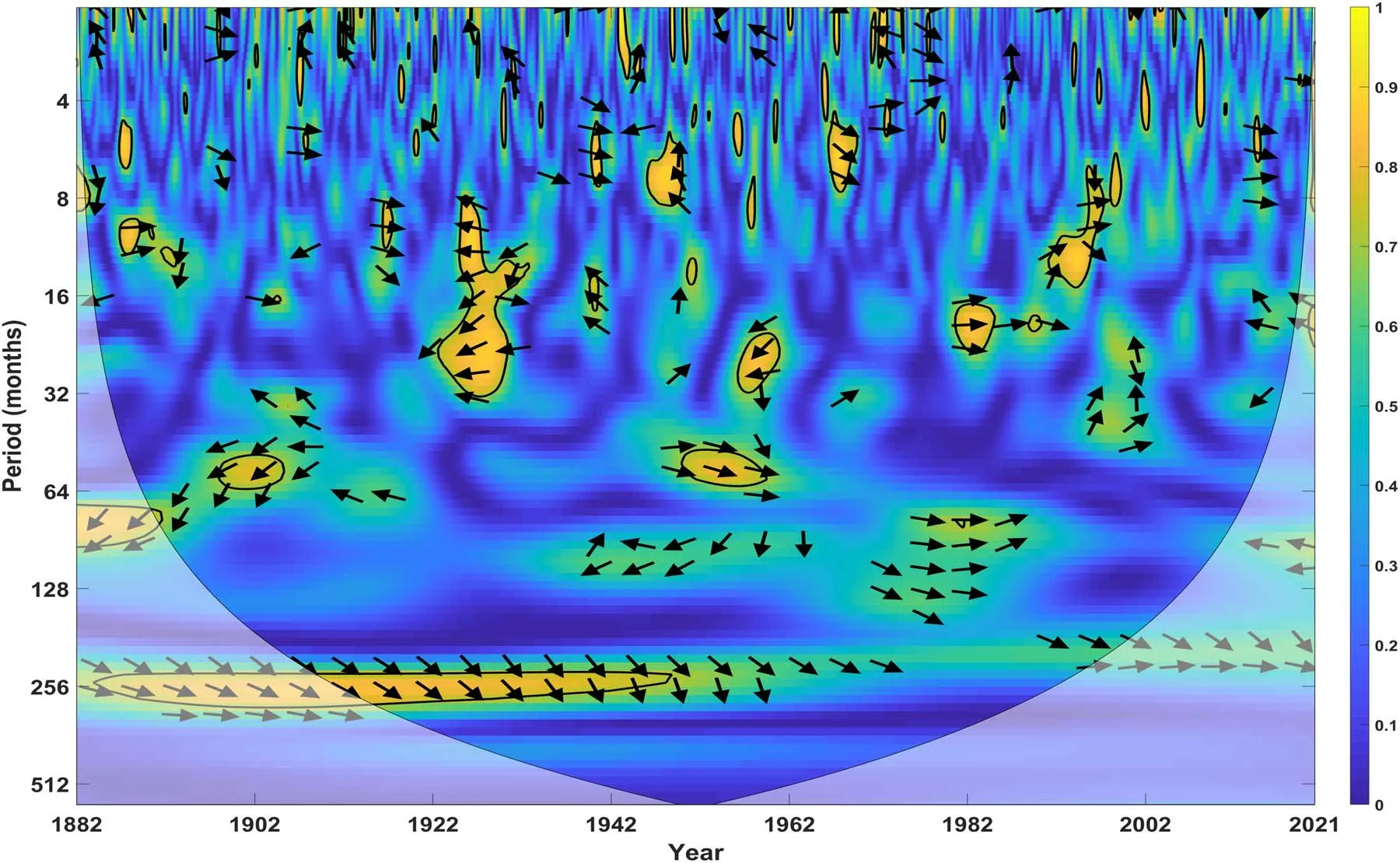
Figure 3. WTC spectrum of monthly TSI and monthly GST from 1882 to 2021.

To explore the influential mechanism of TSI on GST, the WTC is used to expose regions with high local correlation but not necessarily high power in time-frequency domain and further reveal the phase relationship.

In Figure 3, the region surrounded by a bold contour line indicates that it passes the 95% significance level test based on Monte Carlo simulations of the red noise.Only the region where the WTC coefficient is greater than 0.5 shows the phase difference arrow. The arrow which points right implies that the two time series are in-phase; the arrow pointing left means the two time series are in anti-phase; the arrow pointing down indicates TSI leads GST; the arrow which points up expresses that TSI lags GST.From Figure 3 we can see that TSI and GST show a significant correlation at the period around 256 months where the arrows generally points southeast. This indicates that TSI leads GST by about π/4, which is 1/4 of the 256 month period, or 32 months.The WTC result in Figure 3 demonstrates that the effect of TSI on GST is mainly reflected at the timescale around the 256 month or 22 yr cycle, but with an obvious lag.However, the strong correlation is observed only until approximately 1960, after which the link between TSI and GST disappears with the sharp increase in GST. This phenomenon may be attributed to the greenhouse effect caused by the increase of carbon dioxide emissions. Figure 4 displays the annual CO2emissions (specifically global CO2emissions from fossil-fuel burning,cement manufacture and gas flaring)from 1880 to 2014 obtained from the Carbon Dioxide Information Analysis Center database, which is available at http://cdiac.ornal.gov/trends/emis/tre-glob.html. From Figure 4 we can see that due to the fossil-fuel burning, the content of carbon dioxide has increased dramatically since the second industrial revolution in 1960,which is consistent with the change trend of GST. This trend also weakens the connection between TSI and GST.To further study the effect of CO2on GST, the WTC and the wavelet decomposition are employed to comprehensively detect the relationship between GST and CO2from two aspects of period term and long-term trend term respectively.

Figure 5 shows the WTC spectrum of GST and CO2. It is obvious that locally significant correlations are found on timescales of less than 8 yr but with strong phase mixing, and no high correlation zone is observed at timescales of more than 8 yr.The results in Figure 5 suggest that there is no correlation between GST and CO2from the aspect of period term. As shown in Figure 5, WTC mainly focuses on the correlation analysis of periodic terms of two time series in the timefrequency domain, but it does not consider the correlation of trend terms. To compensate for the shortcoming of WTC, the wavelet decomposition is performed until the D5 level and Figure 6 presents the approximation A5 of GST,CO2and TSI,which is the scaling level corresponding to the long-term trend(＞64 yr).

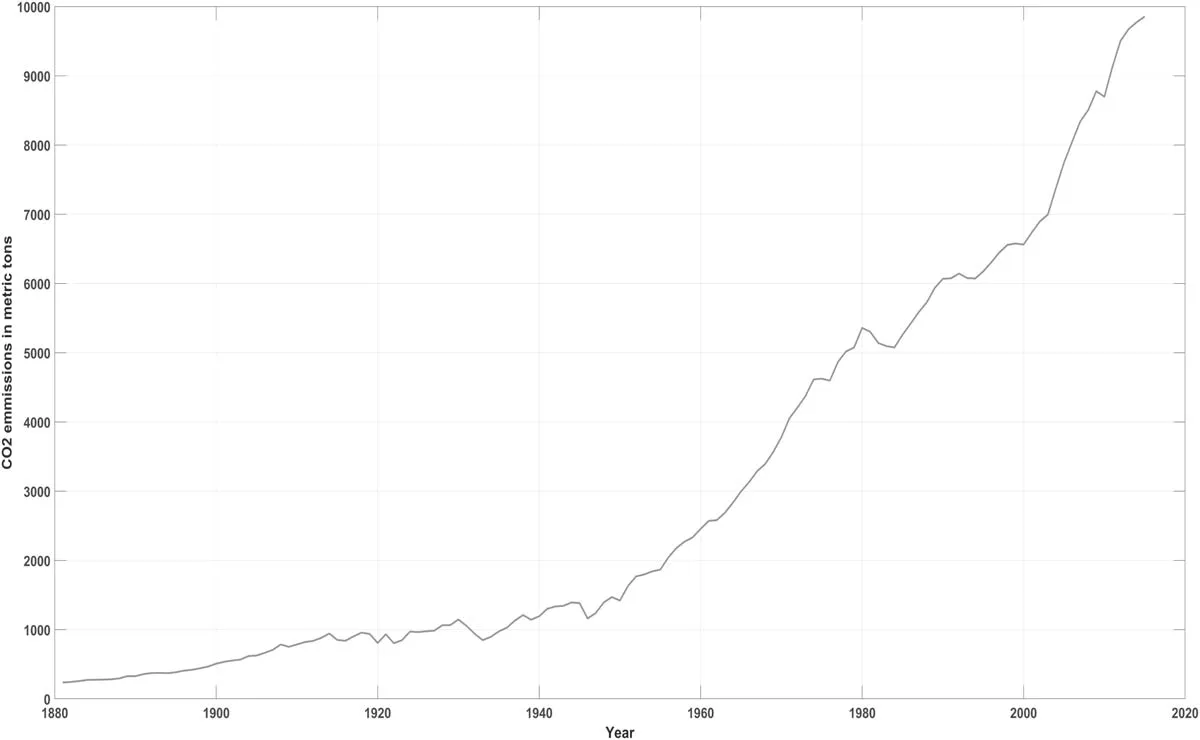
Figure 4. Yearly carbon dioxide emissions from 1882 to 2014.

Figure 5. WTC spectrum of yearly CO2 emissions and yearly GST from 1882 to 2014.

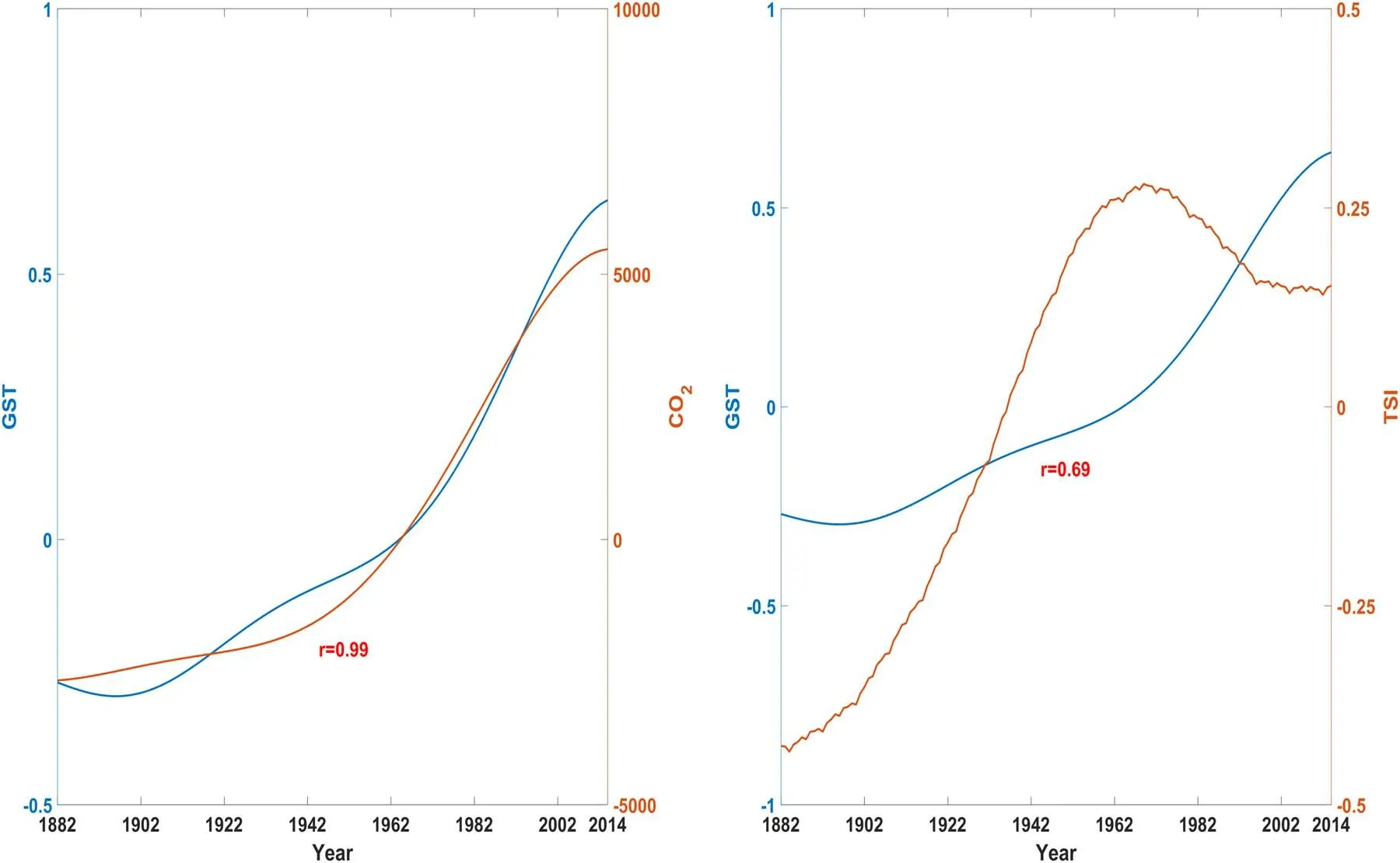
Figure 6.The approximation A5 corresponding to the long term trend of TSI,CO2 emissions and GST after wavelet decomposition,where the approximation A5 of CO2 emissions is the deviation from the 1882–2014 average.

From Figure 6, we can observe that the trend variation of GST is consistent with that of CO2, and the correlation coefficient is as high as 0.99. The trend variation of GST is inconsistent with that of TSI, especially after approximately 1960, when the trend of TSI begins to decline while the trend of GST continues to increase, and the correlation coefficient is only 0.69. A more reasonable result may be obtained by dividing the trend in Figure 6 into two segments before and after 1960 (Table 2).

From the results in Table 2, we can draw the following conclusions: (1) the change of global temperature before 1960 is more correlated with TSI than CO2;(2)the change of global temperature after 1960 is more correlated with CO2than TSI;(3) the contribution of the increasing CO2concentration to the global temperature change tends to be linear. Only by controlling the impact of CO2emissions can we truly reveal the potential relationship between TSI and GST. According to the Augmented Dickey–Fuller test, the time series of GST and CO2emission is non-stationary (Dickey & Fuller 1979). Fornon-stationary time series, a classical regression model cannot be used, which is based on stationary time series. Otherwise,many problems such as spurious regression will appear, and then wrong conclusions will be drawn. To overcome the difficulty of analyzing non-stationary time series, the cointegration theory proposed by Engle and Granger in 1987 provided a solution for modeling non-stationary time series(Engle & Granger 2015). The basic idea of co-integration theory is that although two or more time series are nonstationary, some linear combination of them can be stable.Therefore, there is a long-term stable relationship between these two or more time series, which is called a co-integration relationship. The result of the Engle–Granger co-integration test demonstrates that GST and CO2emissions are cointegrated. This implies that there is a long-term stable equilibrium relationship between GST and CO2emission. We thus regress GST on CO2emissions and apply the ordinary least squares method to estimate the coefficient of the cointegration regression equation.The regression residuals,as the deviations from the equilibrium relationship, represent GST dynamics after controlling the impact of CO2emissions. It should be noted that the CO2emission time series has an annual frequency, so the frequencies of TSI and GST are lowered by averaging the original monthly data to make sure that the frequencies of all three-time series are consistent.

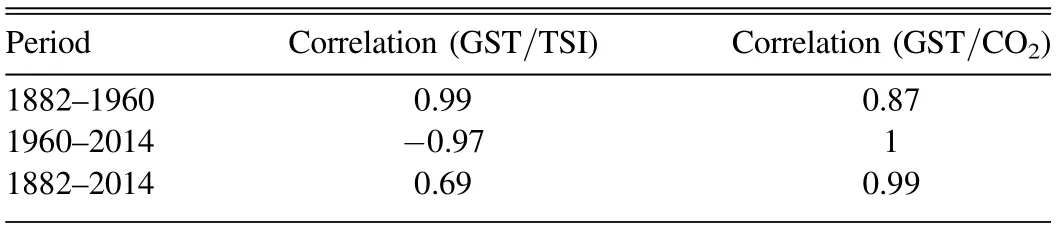
Table 2 Correlation Analysis of the Trend Item of GST, TSI and CO2 Before and After 1960

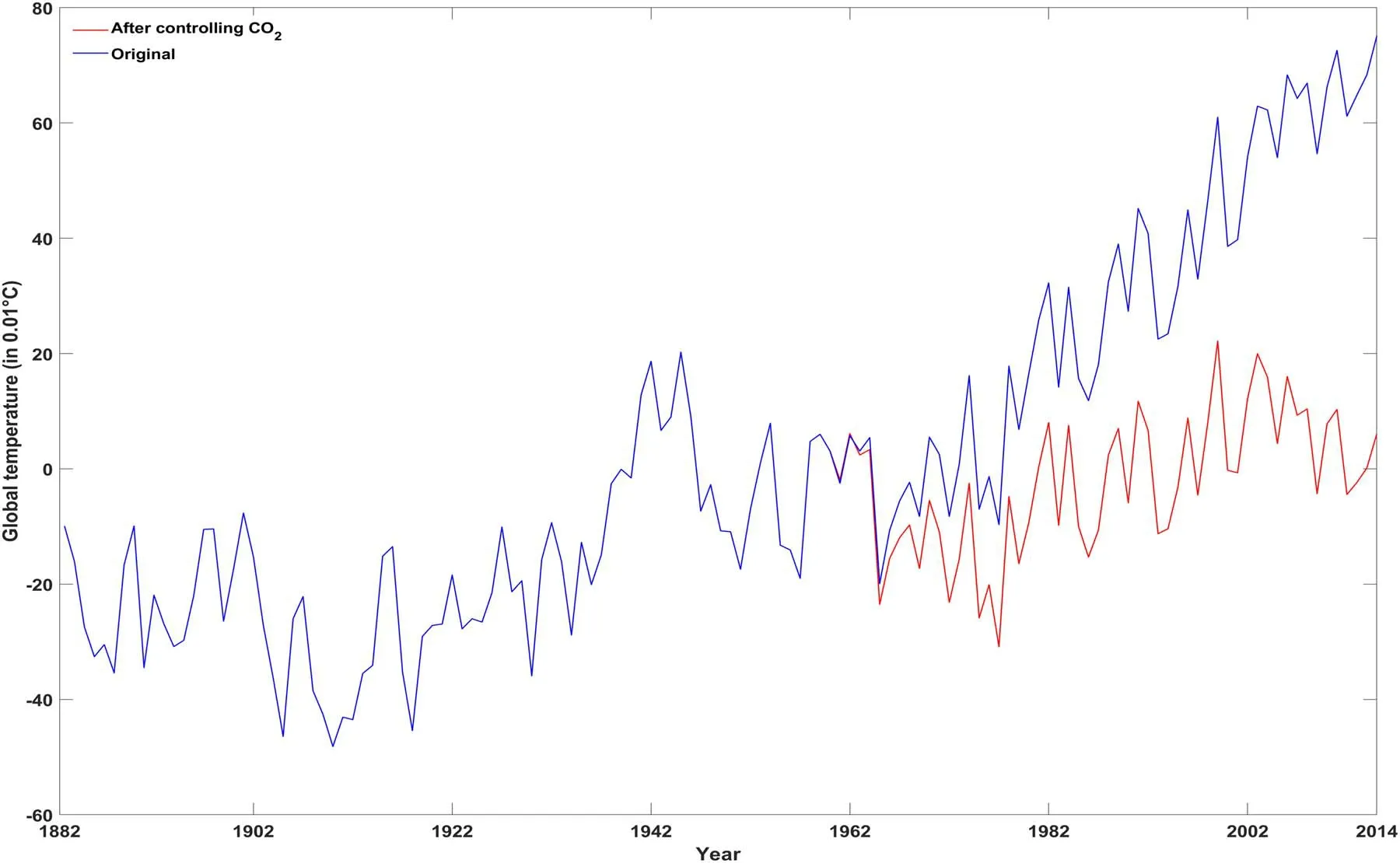
Figure 7. Global land surface temperature time series before and after controlling the CO2 effect.

Since the trend of GST before 1960 is more correlated with TSI than CO2, Figure 7 mainly displays the GST fluctuations from 1960 to 2014 after removing the trend item caused by CO2from GST.From Figure 7 we can clearly see that the trend of GST significantly decreases after 1960 when controlling the impact of CO2emission, which is completely consistent with the results in Table 2. In this way, we could shed light on the true underlying relationship between TSI and GST without the effect of CO2emissions.

Considering the change in frequency, Figure 8 shows the WTC spectrum of yearly TSI and yearly GST before and after controlling the CO2effect.From Figure 8 we can see that after controlling the effect of CO2emissions on GST,the correlation between TSI and GST not only increases considerably but also passes the significance test for the period after 1960. When looking at the significant region with the characteristic scale around 22 yr, we can see that the correlation between TSI and GSI is positive, and the phase difference arrows roughly point to the lower right and fluctuate in a relatively small angle range.Consequently, we adopt the average phase difference to quantitatively express the phase relationship between TSI and GSI,and the average phase difference is 50°.2,which indicates that the changes in TSI precede the changes in GST by 3 yr.It can be seen that the impact of solar activity on the Earth’s climate has a delayed effect, and the change of solar activity can only be shown in the Earth’s climate after several years.The 22 yr cycle,which is depicted by the relationship between TSI and GST in Figure 8, is confusing on the premise of the fact that the TSI is insensitive to the 22 yr solar magnetic cycle as determined by the study of sunspots. The explanations for this problem are structured as follows: (1) the TSI data are partially reconstructed using SN data, and a sunspot does not consider the change in the Sun’s magnetic field polarity every 11 yr cycle. Therefore this is not surprising that TSI is insensitive to the 22 yr solar magnetic cycle (Barnhart &Eichinger 2011); (2) solar activity has a 22 yr cycle as the dominant period which is also named the magnetic Hale cycle(Souza Echer et al. 2009), and GST also has large climate oscillations with the period of about 20 yr (Scafetta 2010); (3)although the 22 yr cycle of sunspots has a lower amplitude or power than the 11 yr significant cycle,the WTC can well reveal regions with a high local correlation of two time series in the time-frequency domain. Notably, the current research cannot determine the physical mechanism that could well explain the impact of solar activity on the Earth’s climate.However,we are inclined to the views of Marsh&Svensmark(2003)that global climate change may be attributed to the variability of solar magnetic field and solar wind, which modulate the flux of galactic cosmic rays reaching the Earth. These galactic cosmic rays may interfere with the atmospheric electric field and cloud cover in turn.

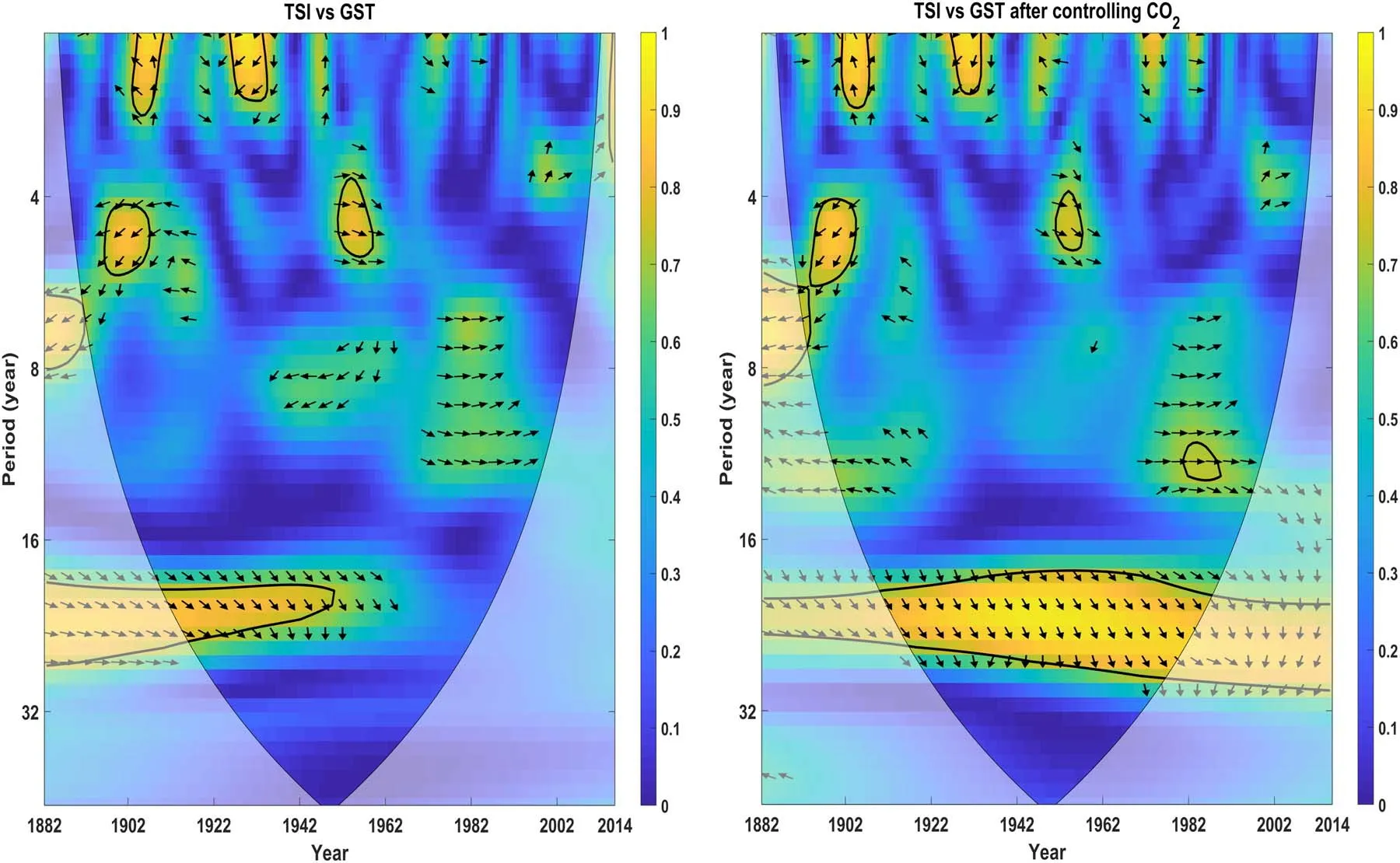
Figure 8.WTC spectrum of yearly TSI and yearly GST before and after controlling the CO2 effect.The right arrow indicates the two time series are in-phase;the left arrow signifies the two time series are in anti-phase;the down arrow shows TSI leads GST(the relative phase angle is positive);the up arrow expresses TSI lags TSI(the relative phase angle is negative).

4. Conclusion

In this study, we examine the relationship between solar activity, CO2emissions and GST. First, the results of CWT indicate that TSI shows a significant oscillation with an 11 yr period while GST has no dominant scale. Then, WTC is applied to confirm that TSI has a positive lag effect on GST,but this connection has been hampered by excessive CO2emissions since 1960. Further, the combination of WTC and WT demonstrates that the effect of CO2emissions on GST is mainly reflected in the trend. Finally, through a co-integration analysis, the relationship between TSI and GST has been reexamined by WTC. The results show that TSI has a positive effect on GST at the characteristic scale around 22 yr with a 3 yr lead.

Acknowledgments

This research is supported by the State Key Laboratory of Geodesy and Earth’s Dynamics, Innovation Academy for Precision Measurement Science and Technology,CAS,Wuhan 430077, China (Grant No. SKLGED2021-2-7).