Boosting Jittering Jets by Neutrino Heating in Core Collapse Supernovae

Noam Soker

Department of Physics, Technion, Haifa, 3200003, Israel; soker@physics.technion.ac.il

Abstract I estimate the energy that neutrino heating adds to the outflow that jets induce in the collapsing core material in core collapse supernovae (CCSNe), and find that this energy crudely doubles the energy that the jets deposit into the outer core. I consider the jittering jets explosion mechanism where there are several stochastic jet-launching episodes,each lasting for about 0.01–0.1 s.The collapsing core material passes through the stalled shock at about 100 km and then slowly flows onto the proto-neutron star(NS).I assume that the proto-NS launches jittering jets,and that the jets break out from the stalled shock. I examine the boosting process by which the high-pressure gas inside the stalled shock,the gain region material,expands alongside the jets and does work on the material that the jets shock,the cocoon.This work is crudely equal to the energy that the original jets carry.I argue that the coupling between instabilities,stochastic rotation,magnetic fields,and jittering jets leads to most CCSN explosions.In other cases,the pre-collapse core is rapidly rotating and therefore ordered rotation replaces stochastic rotation and fixed jets replace jittering jets.

Key words: (stars:) supernovae: general – stars: jets – ISM: supernova remnants

1. Introduction

The collapsing inner core of a massive star in a core collapse supernova (CCSN) releases ＞few×1053erg in gravitational energy. The rest of the star explodes and carries a fraction of⋍0.0001–0.1 of this energy (e.g., Heger et al. 2003;Janka 2012). Neutrinos carry the rest of the energy, while typically only a small fraction of the released gravitational energy ends in radiation.The very inner part of the core forms a nuclear-density compact object at the center, the proto-neutron star (NS). The formation of the proto-NS stops the collapse of the very inner part of the core and sends a shock wave outward.Because of the ram pressure of the collapsing core material the shock stalls at a radius of about Rs⋍100 km. This is the stalled shock. The mass that the proto-NS accretes flows through this stalled shock.

Recent theoretical studies consider two mechanisms to channel a small fraction of the gravitational energy to the exploding outer core and envelope, in case an envelope exists.According to the delayed neutrino mechanism (Bethe &Wilson 1985) neutrinos heat the material in the post-shock zone behind the stalled shock, the gain region, and after some delay the heating revives the stalled shock in a non-spherical manner(e.g.,Nordhaus et al.2012;Couch&Ott 2013;Bruenn et al.2016;Janka et al.2016;O’Connor&Couch 2018;Müller et al. 2019; Burrows & Vartanyan 2021; Fujibayashi et al.2021; Boccioli et al. 2022; Nakamura et al. 2022). According to the jittering jets explosion mechanism (Soker 2010) the proto-NS,or later the newly born NS or a black hole(BH)if it is formed, launches jets that deposit sufficient energy to the collapsing-core material outside the stalled shock and explode the star (e.g., Papish & Soker 2011, 2014b; Gilkis &Soker 2015; Quataert et al. 2019; Soker 2020; Antoni &Quataert 2022; Shishkin & Soker 2022; Soker 2022).

During the explosion there might be several to a few tens of jet-launching episodes. Some typical physical values are as follows (Papish & Soker 2014a). The jets carry a total energy of ⋍1051erg with a typical velocity of ⋍105km s-1and total explosion time of ⋍1 s. Each jet-launching episode lasts for⋍0.01–0.1 s and carries a mass of ≈10-3M⊙. The accretion disk that launches the jets is ten times as massive, so each accretion disk mass at a jet-launching episode is ≈10-2M⊙.In total,during the entire explosion process a mass of ≈0.1 M⊙is accreted through an intermittent accretion disk.

The source of the stochastic angular momentum of the mass that is accreted through the intermittent accretion disk is the stochastic convection motion in the pre-collapse core. The convective cells in the silicon or oxygen burning zones serve as perturbation seeds that instabilities above the newly born NS further amplify to supply stochastic angular momentum with large enough amplitudes to form intermittent accretion disks(e.g., Shishkin & Soker 2022). An important property of the jittering jets explosion mechanism is that the jets of early episodes do not disturb these perturbations for later jetlaunching episodes. The jets do influence somewhat the directions of the later jittering jets (Papish & Soker 2014b).The source of magnetic fields that are required to launch jets is also in the pre-collapse core,from the convective zones as well as the radiative zone above the iron core (Peres et al. 2019).The amplification of the seed angular momentum perturbations,the role of the magnetic field in influencing the stochastic angular momentum (by angular momentum transfer), and the interaction of neutrino-driven convection plumes with the accretion disks are open questions to be determined by future studies of the jittering jets explosion mechanism.

The jittering jets explosion mechanism differs from many studies of jet-driven explosions that assume rapidly rotating pre-collapse cores(e.g.,Khokhlov et al.1999;Aloy et al.2000;MacFadyen et al.2001;Maeda et al.2012;López-Cámara et al.2013; Bromberg & Tchekhovskoy 2016; Nishimura et al.2017; Wang et al. 2019; Grimmett et al. 2021; Perley et al.2021) in the following properties. (1) The jittering jets operate in a negative feedback mechanism (see review by Soker(2016)). This explains why typical explosion energies are several times the binding energy of the ejected mass. (2)According to the jittering jets explosion mechanism most (or even all) CCSNe are driven by jets, even CCSNe of nonrotating cores.In cases of slowly rotating(or non-rotating)precollapse cores, the convective motion in the pre-collapse core(e.g., Gilkis & Soker 2014, 2016; Shishkin & Soker 2021) or envelope (e.g., Quataert et al. 2019) allows the formation of intermittent/stochastic accretion disks or belts that launch jittering jets. Namely, the accretion process through intermittent accretion disks/belts leads to jet-launching episodes where the direction of the symmetry axis of the two opposite jets changes from one episode to the next.

One result of these differences is that there are no failed CCSNe in the jittering jets explosion mechanism framework(e.g.,Gilkis et al.2016;Soker 2017;Antoni&Quataert 2022).This claim has received strong support with the new observational finding by Byrne & Fraser (2022). According to the jittering jets explosion mechanism all massive stars explode, even when the explosion forms a BH. In the jittering jets explosion mechanism the explosion leads to BH formation in the case of a rapidly rotating pre-collapse core.The jets that the newly born NS launches maintain a fixed axis along the large angular momentum axis, and therefore the jets eject only a small fraction of the stellar mass along the polar directions.The rest of the stellar mass collapses to form a BH. The jets lead to a very energetic CCSN,i.e.,some of the most energetic CCSN explosions are those that form BHs (e.g., Gilkis et al.2016;Soker 2017).On the other hand,according to the delayed neutrino mechanism it is possible that a massive star does not explode, but rather most of the mass collapses to form a BH accompanied by a faint transient event (e.g., Nadezhin 1980;Lovegrove & Woosley 2013).

There is no need to form a thin accretion disk that is supported against gravity solely by the centrifugal force to launch jets, although this is the case in many astrophysical objects.Consider a case where the specific angular momentum is smaller than the critical value to support a Keplerian motion around the newly born NS (proto-NS), but the accretion flow does form low-density funnels along the two opposite polar directions (along the angular momentum axis). Schreier &Soker (2016) argued that this accretion belt geometry allows the launching of jets along the polar funnels. Critical to the launching of jets from accretion belts in CCSNe is the presence of very strong magnetic fields (e.g., Schreier & Soker 2016;Soker 2018, 2019a, 2020). This claim, that the compact object at the center of a CCSN can launch jets even when the core does not rotate,but only if there are strong magnetic fields and funnels along the polar directions,has received indirect support from recent three-dimensional (3D) magneto-hydrodynamical simulations of a BH moving through a uniform magnetized medium and accreting mass. In these simulations, Kaaz et al.(2022) find that a BH can launch strong jets despite that the initial angular momentum of the accreted gas is zero,as long as the magnetic fields are sufficiently strong. The ordered magnetic fields that they use form the funnels along the symmetry axis.

In some earlier papers (e.g., Soker 2019b) I mentioned the possibility that there is a mutual influence between stochastic angular momentum accretion and neutrino heating,and that the combined operation of jets and neutrino heating powers CCSNe. In the present paper I study in more detail the way by which neutrino heating in the gain region can boost the outflow that the jets induce. I recall that each jet launching episode is expected to last for ＜0.1 s. Therefore, although the jets of the first pair of jets break out from the stalled shock,there is no time to set an explosion via neutrino heating alone because the delayed neutrino mechanism requires a much longer time to set an explosion (e.g., Bollig et al. 2021). For that, I expect that there will be at least several jet-launching episodes before the end of the explosion process. I present the relevant parameters of the gain region and of the jets in Section 2, and the processes by which the neutrino heating boosts the outflow in Section 3.In Section 4 I discuss some of the assumptions that I make in this study. I summarize in Section 5.

2. Relevant Parameters

2.1. The Ambient Medium

In scaling the quantities for the ambient medium,namely,the medium into which the jets expand, I make use of the detailed study by Janka (2001). I chose specific profiles to demonstrate the boosting processes,but the results are not sensitive to these specific profiles.

I consider the time in the collapse when the stalled shock is more or less static at Rs=100 km and the gain radius is at Rg=50 km. The gain radius is defined to be such that in the zone Rg＜r ＜Rsneutrino heating overcomes neutrino cooling.This zone is made of free nucleons and alpha particles.For the density profile I take (Equation(63)scaled with Figure 3 from Janka 2001)

2.2. The Jets

where δ can vary as the jets expand,i.e.,δ(r,t).Like Papish&Soker (2011) I scale with δ=0.01 that corresponds to a halfopening angle of αj=8°. The density in the jets is

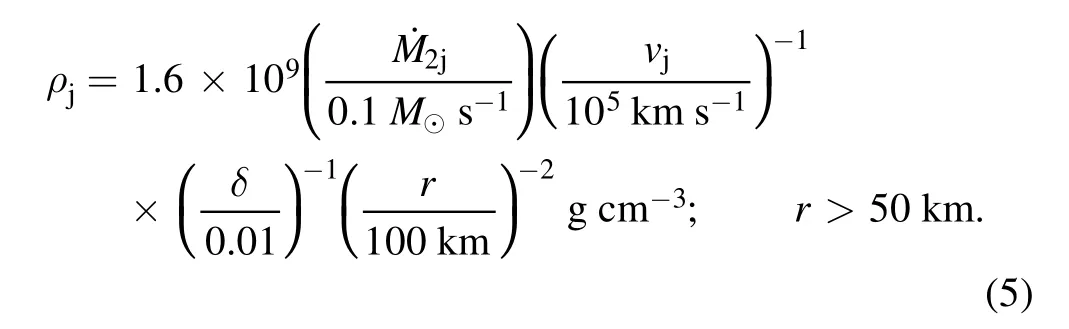
Each jet-launching episode lasts for τj⋍0.01-0.1 s and carries energy of E2j≈few ×1049- few ×1050erg. Note that the jets get their initial energy directly from the accretion energy of the accretion disk,and not from the gain region.The energy from the gain region boosts the outflow that the jets induce.

A possible case for the present setting is one where there are Nlaunch=4, or a few more, jet-launching episodes as I claimed for the supernova remnant SNR 0540-69.3 (Soker 2022), each lasting τj⋍0.03 s or somewhat less. The total energy of the four jet-launching episodes is 1.2×1051erg, which after adding the contribution from neutrino heating that I study here and removing the binding energy of the ejecta gives a typical CCSN explosion energy, i.e., ⋍1051erg. By explosion energy I refer to the kinetic energy of the ejecta, which dominates the explosion energy, plus the radiated energy.

The outcome for the parameters that I use here is that the density in the jets is similar to the density in the gain region.Since the jets’ receive the same amount of neutrino flux from the center, the temperature and pressure inside the pre-shock jets are similar to those in the gain region. Actually, if the thermal pressure in the ambient gas is larger than that inside the jet the ambient medium compresses the jet,while if the ambient thermal pressure is smaller then the cross section of the jet increases.Therefore,the thermal pressures inside the jets and in the ambient gas are about equal. As the pressure close to the proto-NS is much larger than that in the outer gain region(e.g.,Janka 2001), the jets are expected to be collimated. I present the schematic flow structure in Figure 1.

Momentum balance at the head of a jet implies that within the gain region the jet’s head velocity is (e.g.,Papish & Soker 2011)

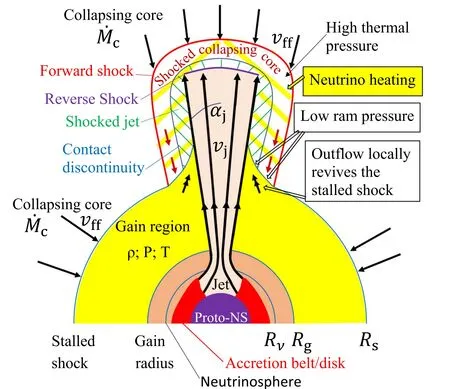
Figure 1.A schematic drawing(not to scale)of the flow structure of one of the two opposite jets just after it breaks out from the gain region.The effects inside boxes that are pointed out with double-lined arrows are those involved in boosting the outflow that the jets induce.The yellow-hatched region is the cocoon,which includes the post-shock material of the jets and of the collapsing core.In the figure the neutrinosphere is outside the proto-NS,which is true only at the very beginning of the process, as in a short time it moves into the proto-NS (e.g., Janka et al. 2007).

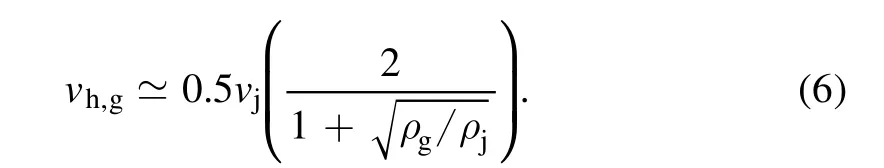
The jet’s head crosses the gain region within Δth,g⋍0.001 s ≾0.1τj.

and I take Rs=100 km. Note that in this approximation I neglect the time variation of the accretion rate (the jets were launched by earlier accreted gas).

To find the velocity of the head of a jet vhas the jet propagates through the collapsing core material we need to equate the ram pressures in the frame of the jet’s head

Just outside the stalled shock at Rs=100 km the velocity of the jet’s head is vh=0.54vj,where I substituted the parameters I use here: vj=105km s-1, β=10, and vff(Rs)=6.1×104km s-1. Papish & Soker (2011) use a different approach to calculate the jet’s head velocity, i.e., they take the ambient density from numerical simulations.Using the same parameters as I do here, their Equation (6) gives a similar value of vh⋍0.54vj. At r=1600 km where vff=1.5×104km s-1the solution of Equation (10) gives a similar value of vh=0.48vj.Namely, the velocity of the jet’s head does not change much near and outside the radius of the stalled shock, and for the parameters that I use here it is

For a jet-launching episode that lasts τj⋍0.03 s the jet reaches a distance ⋍1500 km by the end of the episode.However, the head of the jet will “know”about this at a much later time. For example, if the jet’s head proceeds at half the velocity of the material in the jets it will reach a distance of⋍3000 km before the supply of a fresh jet’s material ceases.This distance is similar to simulations of the jittering jets(Papish & Soker 2014a, 2014b). For a constant jet’s head velocity the interaction will continue until time

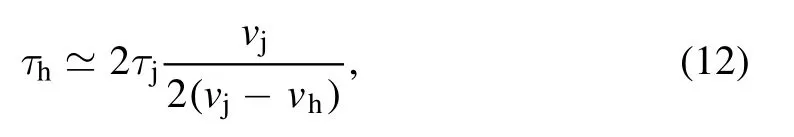
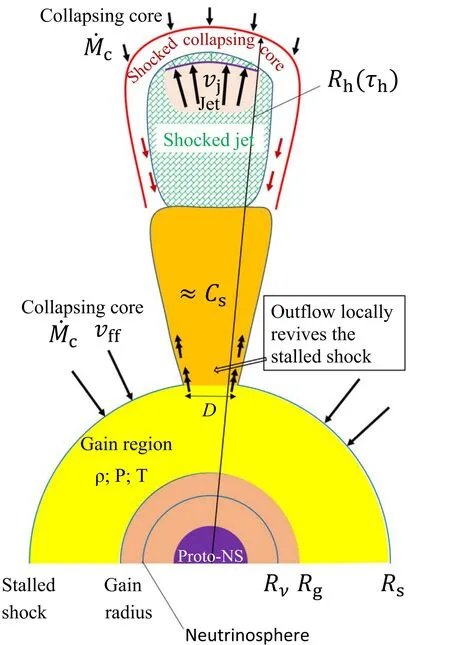
Figure 2.A schematic drawing(not to scale)of the flow structure of one of the two opposite jets just as the jet ceases to feed the head, at τh as given by Equation (12). Note that at late times, unless accretion rate increases a lot, the neutrinosphere is inside the proto-NS.

from the beginning of the jet-launching episode,when the jet’s head reaches a distance of

In Figure 2 I schematically (not to scale) draw the flow at the time τhwhen the jet ceases to feed the head.

The interaction of the jets with the collapsing core is more complicated because neutrino heating and cooling take place in the pre-shock and post-shock media,that of the jets and that of the collapsing core.The post-shock regions of the two media is the “cocoon”. The shock wave that runs into the collapsing core (forward shock) has a size larger than the jet’s radiusrsinαj.

In the rest frame of the jet’s head the collapsing core is shocked at a velocity that is close to about twice as large as its freefall velocity at the stalled shock. This implies that the pressure of the post-shock material of the collapsing core, the“cocoon”, is about three times as large as that just behind the stalled shock. Therefore, the cocoon maintains the collimation of the jet, or might even compress it somewhat.

3. The Boosting Process

In the jittering jets explosion mechanism there are in total several to a few tens of jets-launching episodes, each lasting τj⋍0.01–0.1 s,or even up to a few×0.1 s.In each episode the accretion belt/disk launches two opposite jets. The jets’ axis directions change by a large angle from one episode to the next.Although in Figure 1,which represents one jet in one episode,I draw a straight jet, the jet’s direction might continuously change (precess) by a small angle even within a jet-launching episode.

The interaction of each of the two opposite jets with the collapsing core material shocks both the jet’s material, in the reverse shock, and the collapsing core material, in the forward shock. These two post-shock zones, separated by a contact discontinuity, are referred to as the cocoon (yellow-hatched region in Figure 1).There are two processes by which neutrino heating boosts the outflow of the “cocoon” along the sides of the jets.

3.1. Heating the Cocoon

I first consider the direct heating process where neutrinos directly heat the cocoon. To estimate the importance of this process I estimate the properties of the cocoon. Equation (11)implies that as the jets expand into the collapsing core, at least for r ≾2000 km,both the jets’material and the collapsing core that the jets interact with pass through strong shocks, e.g.,shock velocities of ⋍5×104–105km s-1.This is similar to the velocity by which the collapsing core hits the stalled shock away from the jets. Therefore, the post-shock jets and collapsing core zones, the “cocoon” (see Figure 1), are nearly fully composed of free nucleons. This in turns implies an efficient neutrino heating, similar to that in the gain region.

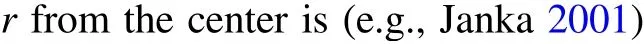
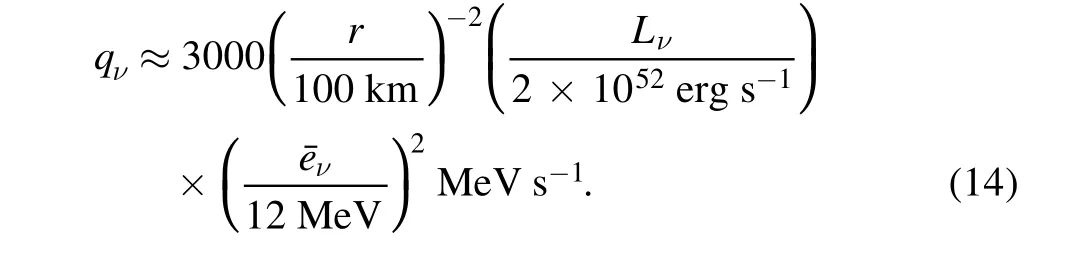
I present here a very crude estimate, since only hydrodynamical simulations of the interaction of the jets with the collapsing core can find the total heating of the cocoon.Consider that the jets shock and drag out collapsing core material of equal mass.This means that each nucleon in the jets drags another nucleon from the collapsing core. Although the interaction region moves out, there must be material between the jet’s head and the stalled shock.I consider that this material flows outward at a speed of vcocoon≈0.5vj⋍5×104km s-1.To find the total heating of the cocoon per nucleon in the jet I integrate over time dt=dr/vcocoonfrom r=100 km out and multiply by two,as for each nucleon in the jet there are two in the cocoon.I find that for each original nucleon in the jet direct neutrino heating of the cocoon adds energy of

3.2. Accelerating the Cocoon Out

With the parameters of Equations(1)–(3)the sound speed of the gain region at r ≾Rsis

where in the second equality I used Equation (11). The collapsing core material along the jet’s axis and around it is shocked by the jet, and therefore reaches the stalled shock at a slower velocity than that of the undisturbed collapsing core material. As a result of that, the ram pressure on the stalled shock around the jet, namely, where the cocoon touches the stalled shock (see Figure 1), is much lower than that of the undisturbed collapsing core material. This leads the highpressure gas just behind the stalled shock to stream into the cocoon (the arrows with a double-triangle head). This adds energy to the cocoon. In other words, the material in the gain region locally revives the stalled shock (Figure 1) and does work on the cocoon.

Only full two-dimensional (2D) or 3D hydrodynamical simulations can determine the extra work that the gas from the gain region does on the cocoon. I here only crudely estimate a plausible value. Consider that the cocoon cross section on the stalled shock is b ⋍few times the cross section of the jet. The combined cross sections of the two opposite cocoons(only one is shown in Figure 1) are

I comment on the two main assumptions that I used in deriving Equation (18). (1) The gain region expands at the sound speed into the cocoon.The reason is that,as I discussed above, the pressure in the gain region is much larger than the pressure of the cocoon. The typical velocity by which a high pressure zone expands into a much lower pressure zone is the sound speed. In other words, I assume that the initial thermal and kinetic energy of the cocoon near the stalled shock is negligible. (2) The pressure inside the stalled shock does not drop despite the expansion along the cocoon. This assumption is based on the inequality bδ ≪1. Namely, the area through which the gas in the gain region expands out is small.Collapsing core material continues to fall on most of the other area of the stalled-shock sphere and therefore maintains the pressure there. Moreover, if the pressure in the gain region drops the stalled shock moves inward and this, as I indicated above, increases the work done according to Equation (18)asRs-1.

3.3. Relation to the Standing Accretion Shock Instability (SASI)

In the SASI the stalled shock surface oscillates with a large departure from spherical symmetry (e.g., Blondin et al. 2003;Ohnishi et al.2006).Because the ram pressure of the collapsing core varies as ∝R-5/2(e.g.,Blondin&Mezzacappa 2006),the ram pressure on a small protrusion of the stalled shock surface into the collapsing core(toward larger radius)is lower than on the rest of the stalled shock. This protrusion then grows.Simulations find that the l=1 and l=2 modes dominate the SASI (e.g., Blondin & Mezzacappa 2006; Ohnishi et al. 2006;Hanke et al. 2013). Blondin et al. (2003) worked out the physics of SASI and wrote that if neutrino heating supports the stalled shock for a sufficiently long period of time the SASI might initiate the explosion. Blondin et al. (2003) further discussed the possible coupling between rotation, magnetic fields, and SASI, as later numerical simulations show (e.g.,Summa et al. 2018).

The effect by which the gain region does work on the cocoon, i.e., the shocked material of the jets and of the collapsing core around the jets (Section 3.2) is similar to the way the SASI facilitates explosion in the frame of the delayed neutrino explosion mechanism. The differences are that in the jittering jets explosion mechanism the perturbations that the jets cause are non-linear to start with(see Figure 1 and 2),and that they are on smaller scales. Consider that the diameter of the cross section of the cocoon on the stalled shock surface(Figure 2) is D ⋍(8bδ)1/2Rs, where b and δ are given by Equations (17) and (4), respectively. This corresponds to a mode of order

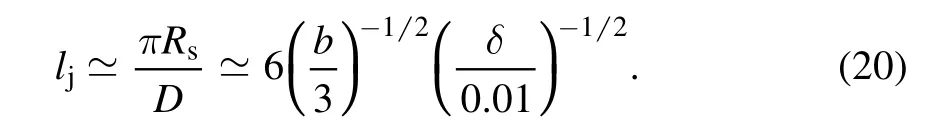
It is quite likely that the next jet-launching episode starts while the outflow from the gain region along the jets of the previous jet-launching episode has not ended yet.Namely,for a short time the perturbations by the jets occur at four places simultaneously.

The conclusion is that the jets might excite SASI-like oscillations with lj⋍6 in addition to the l=1 and l=2 of the SASI itself.

In a recent study, Vartanyan et al. (2022) examine the turbulence that develops below the stalled shock as a result of pre-collapse perturbations in the core.They find that the power spectra of tangential velocities in the turbulence zone are relatively flat up to spherical harmonic index l ≾4, and from there on a Kolmogorov-like spectrum forms. In the range 4 ≾l ≾10 the modes have energies ⋍0.2–1 (depending on the 3D progenitor model) times the energy of the l ≾4 modes.However, the seed perturbations in those simulations are small(in the linear regime). Here I suggest that the non-linear perturbations that the jets introduce might excite the l ⋍6 SASI modes. My suggestion requires of course to be confirmed by 3D simulations.

4. On the Assumptions

I here discuss the challenges and difficulties that the proposed boosting process should overcome before it stands on solid ground.

4.1. Motivation

Before discussing the challenges of the jittering jets explosion mechanism I comment that there is a place to discuss the jittering jets explosion mechanism because of the imprints of jets in many supernova remnants (e.g., Bear et al.2017; Grichener & Soker 2017; Yu & Fang 2018; Lu et al.2021; Soker 2022), and because of the difficulties of the delayed neutrino mechanism. Among several difficulties (e.g.,Kushnir 2015;Papish et al.2015),the two main disadvantages of the delayed neutrino mechanism are that the maximum explosion energy that can be explained is ⋍2×1051erg (e.g.,Fryer et al.2012;Sukhbold et al.2016),and that in some cases explosion does not occur at all (e.g., Burrows et al. 2020),although in many other cases explosion does take place in simulations (e.g., Bollig et al. 2021; Burrows &Vartanyan 2021).

4.2. The Available Explosion Energy

This is compatible with observed energies of CCSNe as in most cases Δmconv＞0.03 M⊙(Shishkin & Soker 2022).

4.3. The Timescale of the Boosting Process

4.3.1. Comments on Equation (19)

In Section 3.2 I estimated the outflow timescale of the gain region material to be several times the jets’ activity phase,τg,out=several×τj. As stated, this estimate should be confirmed with 2D or 3D numerical simulations.Here I further describe the process and the uncertainty in this timescale.

After the jet activity ceases, the material in the gain region closes the funnel that each jet opened in the post-stalled shock zone in about a sound crossing time, Δtfunnel,g⋍D/Cs(Rs)⋍5×10-4s for a jet with a half opening angle of 8° and sound speed as in Equation (16). This very short timescale works for the proposed mechanism because it implies that practically the gain region starts to impart force on the cocoon (Figure 2)immediately.

The cocoon itself closes the funnel that the jet has opened outside the gain region (above the stalled shock). Because the cocoon is the post-shock media after it expanded, its temperature is lower than the immediate post-shock temperatures of the shocked collapsing core and of the jet near its head.Nonetheless, its sound speed is expected to be very large,definitely much larger than 1% of the jet velocity, i.e.,Cs(cocoon)＞1000 km s-1. It will close the funnel at rh=3000 km in a timescale of Δtfunnel,3000＜0.4 s for the same parameters that I use throughout the paper (see Equation (13)). As this is about the time I estimated,τg,out=10τj⋍0.3 s (see Equation (19)), I conclude that the cocoon also closes the funnel at any radius r before the outflow that the gain region accelerates reaches that radius.

I emphasize that although the cocoon closes the funnel,unlike the collapsing core, the cocoon does not fall toward the center at a high speed.As well,due to its high thermal pressure as a post-shock gas, its density is lower than that of the collapsing core. In other words, the jets pushed the gas to the sides as they expand outward.This will allow the high-pressure gas in the gain region to expand and further accelerate the cocoon to high velocities.

To summarize this section I emphasize again the implication of Equation(19)and the discussion above.What I have shown is that the mechanism by which the delayed neutrinos explode stars, when it manages to work, is more efficient when we consider jets that locally revive the stalled shock. If this mechanism does not work here, the delayed neutrino mechanism will not work either.What I further argue is that in many cases where the delayed neutrino mechanism does not work,the jittering jets explosion mechanism can work,and further be boosted by neutrino heating. As well, the jittering jets mechanism can account for explosion energies much above 2×1051erg.

4.3.2. On the Possibility of Prolonged Jet Activity

The jittering jets mechanism was developed to explode stars within about a second from core bounce, similar to the expectations from the delayed neutrino mechanism in the past.Some recent studies suggest that the explosion activity can last for over five seconds (e.g., Bollig et al. 2021), while other studies, however, argue that the explosion should take place within less than a second(e.g.,Saito et al.2022).The accretion rate in a fraction of the first second is indeed close to 1 M⊙s-1,as I scale quantities in this study. The accretion rate in the simulation of Bollig et al.(2021)from t=1 s to t=6 s is about 0.01 M⊙s-1. The total accreted mass might be ⋍0.05 M⊙in this time period. The proto-NS radius is smaller at these late times, RPNs⋍15–20 km. Substituting this accreted mass and the smaller proto-NS radius in Equation (21), I derive an energy that might be comparable to or larger than the energy that the jets carry in the first second. Namely, the jets can supply more energy if the process of accretion continues.

The prolonged jet activity has the advantage that at later times core material from further out is accreted, and those zones further out might in some cases posses strong precollapse convection that seeds the instabilities that feed the stochastic angular momentum of the accreted gas (e.g.,Shishkin & Soker 2022).

4.4. The Launching of Jets

The process that most severely needs confirmation by 3D simulations is the launching of the jittering jets by the intermittent accretion disk/belt that the accreted mass with stochastic angular momentum forms. These simulations must include magnetic fields(e.g.,Soker 2018,2019a,2020),and be of very high resolution.For that,I do not expect simulations at present to be able to launch jets.

Critical to the launching process is the formation of two opposite funnels near the proto-NS. The accretion disk/belt launches the two opposite jets through these funnels (e.g.,Schreier & Soker 2016). Like the disk, the funnels are intermittent and change their direction in a stochastic manner,giving rise to jittering jets. Magnetic fields can form such funnels, as well as the stochastic angular momentum of the accreted gas. But even when the angular momentum of the accreted gas opens funnels along the angular momentum axis,magnetic fields are crucial to channel accretion energy to the collimated outflow.

As I mentioned in Section 1, the simulations by Kaaz et al.(2022) suggest that such a process is possible. Kaaz et al.(2022) simulate cases of a BH that accretes mass as it moves through a magnetized homogeneous medium, i.e., the Bondi-Hoyle-Lyttleton accretion flow. The initial direction of the magnetic field lines is perpendicular to the direction of BH motion through the medium. They obtain jets more or less along the initial direction of the magnetic field lines, despite that there is no initial angular momentum in the flow.However,for jets to be launched the magnetic fields have to be sufficiently strong.

I therefore conclude that the fact that present simulations do not obtain jittering jets cannot be used to rule out such jets,simply because these simulations do not have yet all ingredients that might lead to such jets.

5. Summary

I conducted a study to crudely estimate the boosting of jittering jets by neutrino heating. In the jittering jets explosion mechanism where there are several or more jet-launching episodes, the jets of one jet-launching episode are active for a relatively short time and do not carry enough energy to explode the core. It is the additive effect of several and more jetlaunching episodes that eventually explodes the star.

I chose a set of parameters for the ambient gas and jets(Section 2) to perform the calculations. I then studied two processes by which neutrino heating can increase the energy that the jets deposit to the collapsing core material.

In Section 3.3 I raised the possibility that the jets excite SASI-like oscillations but with higher orders of l ⋍6(Equation (20)) with respect to the regular SASI models that have mainly l=1 or l=2. These modes exist alongside the regular SASI modes.

Blondin et al. (2003) mentioned the possible coupling between neutrino heating, the SASI, rotation, and magnetic fields,in exploding CCSNe.The spiral modes of SASI amplify initial perturbations to supply the stochastic angular momentum to the accreted gas that launches the jittering jets(e.g.,Shishkin& Soker 2021), and strong magnetic fields are involved in launching the jets (Sections 1 and 4.4). In the present study I strengthen the claim for a mutual influence between jittering jets and neutrino heating. I therefore extend the statement of Blondin et al. (2003) to include also jets, and argue that the coupling between spiral-SASI, stochastic rotation, possible ordered rotation, magnetic fields, and (jittering) jets leads to the explosion of CCSNe.

In Section 4 I discussed some of the assumptions of the present study. Although the launching of jittering jets is impossible to include in present numerical studies(Section 4.4), I encourage simulations to insert jittering jets near the stalled shock and study the effects of neutrino heating on these jets and the outflow they induce.

Acknowledgments

I thank Dima Shishkin for helpful comments, and an anonymous referee for detailed and very useful comments.This research was supported by a grant from the Israel Science Foundation (769/20).

Data availability

The data underlying this article will be shared on reasonable request to the corresponding author.