自愈理念下DCC与TRIZ集成的设计方法研究

郭昆

自愈理念下DCC与TRIZ集成的设计方法研究

郭昆

（河北工业大学 机械工程学院，天津 300130）

为提高复杂系统的稳定性，将自愈理念引入复杂系统概念设计阶段，结合设计过程复杂性（DCC）与发明问题解决理论（TRIZ），提出一种自愈理念下DCC与TRIZ集成的设计方法。首先，对系统进行功能分析，并通过DCC理论判断系统中功能的实现概率；其次，确定实现概率低的潜在问题功能，对这些功能进行自愈设计；之后，使用TRIZ工具解决出现的问题；最后，将上述过程集成，形成自愈理念下DCC与TRIZ集成的过程模型。通过一个密集柜车库的案例验证了过程模型的有效性。

自愈理念；设计过程复杂性；TRIZ；概念设计

在工程实践中，大多数的装备故障不是突发性的[1]，而是由疲劳、磨损、偏差等累积造成，是渐进性的。若能在故障初始形态时便通过装备本身的智能调控系统进行消除，无疑是解决故障的最佳手段。为实现这一目标，高金吉[2]提出“故障自愈化”的原理，希望可以通过复杂系统的自我检测修复愈合来保证系统的稳定运行。在此基础上，研究者们为自愈理论的发展做出了巨大贡献。王仲生等[3]在对飞行器早期故障自愈机理进行分析的基础上，建立了飞行器早期故障自愈模型。黄利权等[4]根据自愈的理念提出一种转子同频振动的在线消除策略，实现同频振动的在线消除。马晋等[5]提出基于瞬时转速波动率的内燃机故障诊断方法，实现内燃机点火状态的早期预警。随着“故障自愈化”的原理在工程领域的不断应用，高金吉[1]进一步提出“人工自愈（Artificial self- recovery，AS）”概念，将复杂系统自愈研究推向了一个全新的高度。

自愈理论在复杂装备领域中应用较为广泛，且还在不断地发展成熟。姚剑飞等[6]通过构建靶向自愈调控系统，有效解决了在透平机中一直存在工作中转子不平衡的振动故障问题。Yang等[7]提出一种由太阳能电池和一个自修复摩擦发电纳米发电机组成的混合能源系统，解决了太阳能电池的潜在机械损坏导致其输出能力降低的问题。Huang等[8]提出一种基于有机水凝胶的自修复摩擦发电纳米发电机，在实际应用方面拥有可靠的输出性能和自我修复能力。

目前自愈理论的发展逐渐深入化、全面化，覆盖了各个领域。若将自愈理论引入系统的概念设计阶段，会给复杂系统长期稳定运行提供良好的保障。

将自愈理念应用于复杂系统的设计阶段需要充分考虑系统中具有的强耦合、非线性、时变性和开放性等特征的复杂特性。Suh[9-10]提出了设计过程复杂性（Design-Centric Complexity，DCC）理论的概念。该理论主要研究复杂系统在设计过程中产生的复杂性，以系统设计时功能的实现概率为切入点，并以概率的高低评价系统的复杂性程度[11]。这与自愈的理念相契合。

本文采用自愈理念，在设计阶段通过对系统功能的分析与设计使系统具有自愈能力。在此基础上，对相关理论进行了研究，并提出自愈理念下DCC与TRIZ（Theory of the Solution of Inventive Problems，发明问题解决理论）集成的设计方法。

1 相关理论

1.1 人工自愈理论

当一个正常工作的复杂系统发生微小变化时，该系统一般可以自适应地继续保持正常工作，而当系统发生较大变化或有其他干扰时，该系统将会发生故障等异常状态。为避免因停机维修造成大量的人力物力损失，人工自愈理论近几年被推上了学术界的风口。

人工自愈是一种以工程自愈为基础，来自仿生机械学研究的理论。它是由中医学中的自主调理引发出来的理念，将人和动物的自愈机制赋予机械系统，使机械系统储存、补充和调动自愈力，以维持机体健康状态[12]。

人工自愈理论借鉴现代医学，以故障诊断为基础，研究以故障预防和消除为目标的自主调控和自修复技术。建立了包含数据获取、信息认知、科学决策、精准执行的理论框架，并在上述框架的基础上得到机器自愈调控系统。自愈理念调控系统模型如图1所示。

细线代表普通流程；粗白线代表数据传递；粗黑线代表更高级的系统传递。

1.2 公理设计理论

在公理设计框架中，从一个领域到另一个领域的映射包含了组织决策、技术决策、产品设计和创建过程中应用的过程信息。

利用公理设计的自顶向下的分解过程，通过功能域和结构域之间的映射，同时考虑功能需求与设计参数之间的关系。可更好地对系统的功能及其对应的结构进行分析。如图2所示。

FR为功能；DP为结构。

1.3 TRIZ理论

TRIZ理论是用来解决问题的一种工具，其认为冲突普遍存在于各种产品与设计之中[17]。冲突主要分为两类，即物理冲突和技术冲突。其中物理冲突指为了实现某种功能，子系统或元件应具有一种特性，但同时出现了与该特性要求相反的特性。技术冲突是指一个作用同时导致有用及有害两种结果，也可指有用作用的引入或有害效应的消除导致一个或几个子系统或整个系统变坏。

2 DCC角度下的故障机理与自愈方式

在DCC理论中，系统所具有的设计过程复杂性大小能够用功能实现概率进行表征，可以看作是产品功能需求的设计范围与系统范围之间关系的函数，如图3所示。

系统中功能所具有的信息含量大小是计算功能实现概率高低的决定性因素。由于系统存在耦合性或时变性等因素，系统范围不会如初始值一样不发生变化，系统范围的改变，将会造成功能实现概率的变化[14-15]。

图3 功能需求的概率密度函数[13]

2.1 故障系统偏差

从设计过程复杂性的角度看，功能失效的根本原因是系统范围偏离了设计范围，产生的机理可分为两种类型，如图4所示。其中，在第一种偏离方式下，系统范围的“公差带”变宽，其对称中心偏离设计范围的中心。

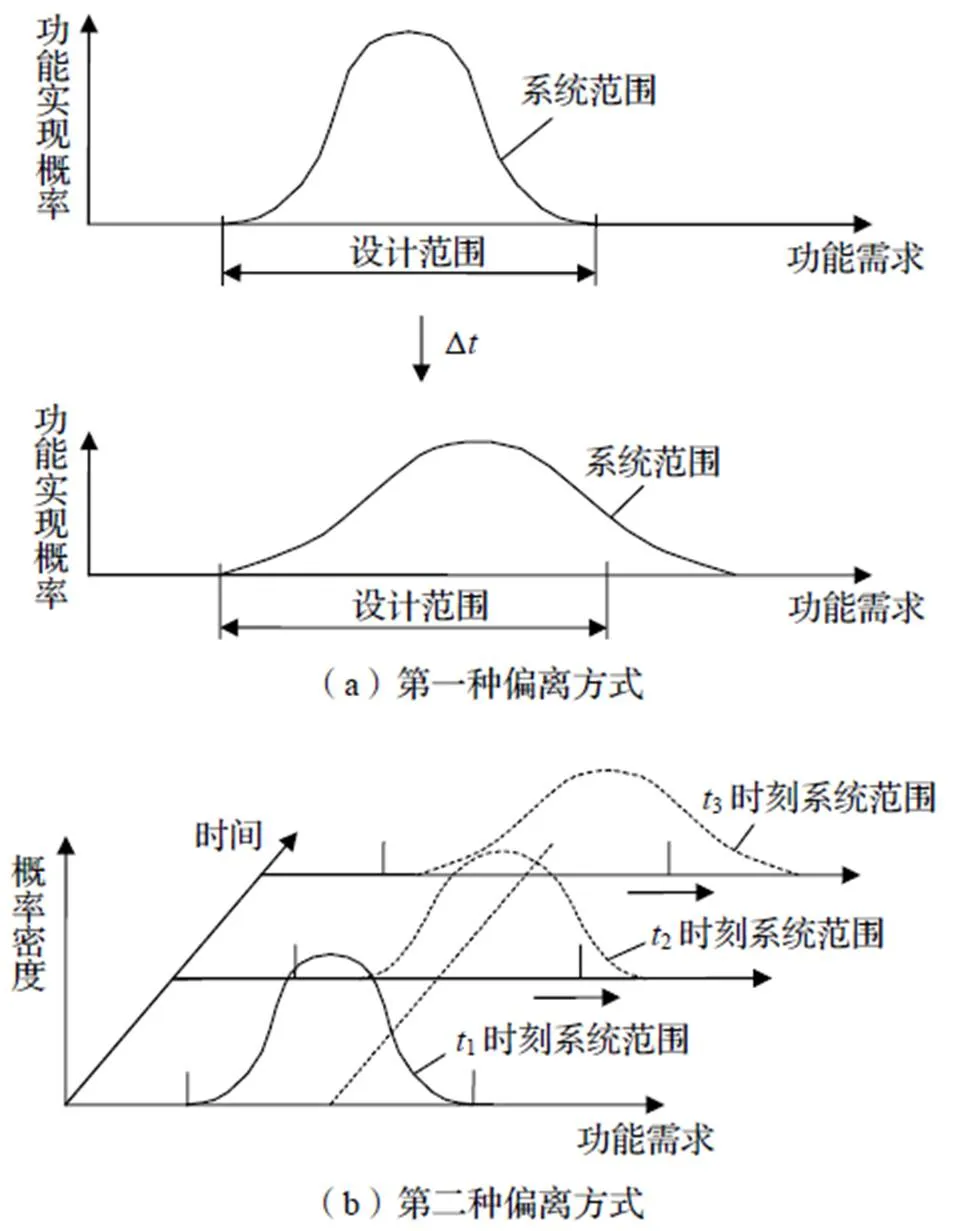
图4 两种偏离方式的系统范围变化

两种系统范围变化的最主要的区别是变化的时间不同。虽然最终的变化状态相同，但一般有：

(2－0)＞＞Δ（1）

式中：0为初始时刻系统范围。

系统范围降级后能恢复其初始分布，系统功能具有的这种特性被称为周期性。所以可以引入设计过程中常用的建立功能周期解决时间相关组合复杂性的方法解决系统故障问题，如图5所示。

图5 引入功能周期的系统范围变化

然而并不是所有故障都适合引入功能周期进行解决，需要根据功能实现概率及概率变化率进一步判断。概率变化率可表示为：

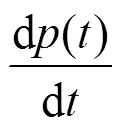
式中：()为概率变化率；()为某一时刻的功能实现概率，0≤()≤1；为时间。

根据系统的功能概率函数的分布情况，判断结果可分为三类偏差产生机理。

（1）∀，使()存在。表示为1。

含义为：此功能的系统范围是逐渐偏离设计范围的。则系统功能的第一种偏差产生机理的故障可以引入功能周期进行解决。

（2）∃1，使(1)不存在，且(1＋Δ)＞0。表示为2。

含义为：此功能的系统范围相对于设计范围发生了突变，但系统范围并无脱离设计范围。

设为满足系统功能需求的最低概率，则2包含两种情况：当(1＋Δ)＞（Δ趋于无穷小）时，为2I情况；当(1＋Δ)＜时，则不可以引入功能周期，为2II情况。

2＝2I∪2II（3）

（3）∃1，使(1)不存在，且(1＋Δ)＝0。表示为3。

含义为：此功能的系统范围相对于设计范围发生了突变，且系统范围已脱离设计范围。

2.2 自愈方式分类与选择

通过上述设计过程复杂性与自愈理论的介绍可以看出，故障自愈过程与设计过程复杂性理论存在一定的对应关系。系统功能实现概率正常－减小－正常的过程可以看作系统功能出现问题之后自愈的过程。

从改变功能实现概率的角度出发，实现自愈的方法可分为三种：①初始化自愈，指不需要额外的调控，只需对装备进行初始化操作；②自身自愈，指系统利用系统存在的可用资源，通过整合来满足功能需求；③辅助自愈，指通过额外增加智能辅助调控装置进行的自愈。在设计过程中，针对不同系统需依据工作要求选择适当的自愈方式。

采取初始化自愈方式解决系统运行中出现的故障问题，易导致系统的制品出现问题，造成损失。

自身自愈与辅助自愈在原理上均是采取对问题功能结构添加新的偏差补偿结构的方式进行自愈。两者具体的区别为：自身自愈采用整个系统内的可用资源，通过连接与转化结构实现问题功能的自愈；辅助自愈则需要系统外的资源，为问题功能添加偏差补偿机构。这两种自愈方法的具体选择过程如下。

（1）在公理设计的功构映射的基础上，建立设计矩阵，为：

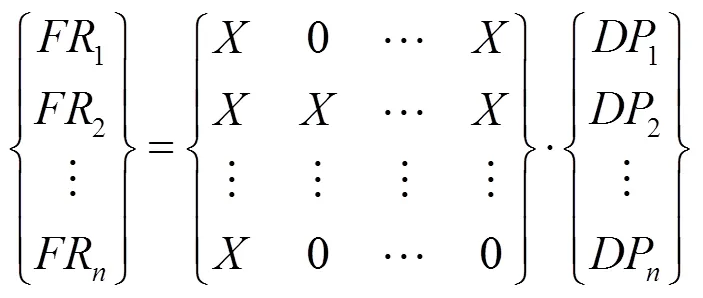
（2）针对问题功能进行变换，确定可行的偏差补偿结构(FR)。一般的，经过变换会得到几个合适的解。下文将直接用1、2、3代表偏差补偿结构所涉及的结构参数集合。以1为例进行解算。通过系统内结构的组合可以得出偏差补偿功能结构的实现表达式为：

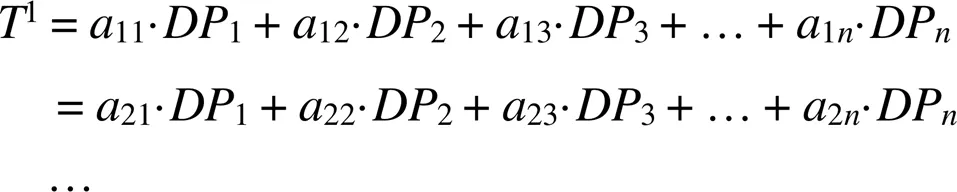
式中：a为0或1的二进制数。

由式（4）可得：

将式（5）的矩阵形式代入式（6），得：

则偏差补偿功能与现有功能的耦合关联矩阵为：

耦合关联矩阵表达了新添加的偏差补偿功能与其他功能的耦合情况。选取矩阵中含零元素最多的行向量，即为耦合程度最低的解。若系统内的结构参数无法满足偏差补偿功能，或者在整合结构的过程中存在较高的复杂性，则只能选择利用外部资源建立偏差补偿功能的结构，即采用辅助自愈方式，反之则可以选择自身自愈方式。

3 自愈理念下DCC与TRIZ集成的过程模型

在上述理论研究的基础上提出自愈理念下DCC与TRIZ集成的过程模型，如图6所示。具体步骤如下：

（1）对目标系统的功能和结构分别进行分析；

（2）根据设计需求，寻找存在潜在问题的功能；

（3）利用功能实现概率导数法判断问题功能所对应的系统范围变化类型；

（4）对符合自愈设计要求的问题功能，通过设计矩阵变换选择自愈方式，并使用TRIZ工具解决系统中存在的问题，得出最终方案。

图6 自愈理念下DCC与TRIZ集成的过程模型

4 工程实例分析及验证

中国汽车工业协会相关数据[18]显示，2021年上半年国内汽车销量仍保持一个相对较高的增速。城市中心的汽车保有量更是迅速增加，城市泊车愈发困难。在此背景下，通过分析国内外对智能泊车的研究，并结合中心城区土地资源稀缺的情况，提出一种密集柜式智能立体车库，如图7所示。设计了可移动式泊车位，当需要泊车时，车位自动打开，自动泊车装置将汽车移到对应的车位上，泊车完毕后，车位收缩进入密集柜回到原位。通过设计减少了泊车道的数量，从而有效减少了占地面积。

图7 密集柜车库

现有密集柜车库在使用方面仍有待改进，通过自愈理念下DCC与TRIZ集成的过程模型对密集柜车库进行分析与设计，在得到良好方案的同时验证了过程模型的有效性。具体步骤如下。

（1）对密集柜车库进行功能分析。如图8所示，首先分解总功能，得到三个分功能，然后将三个分功能进一步分解至功能元。功能分解之后，运用公理设计理论采用之字形映射的方式，将功能映射到结构域。如：存储汽车功能映射到结构域为存放单元、移动车位功能映射到结构域为移动装置。具体结构映射结果如图9所示。

（2）车库的首要要求是安全。一般车库多为固定式，其框架为水泥钢筋搭建，结构稳定、承载能力强，对于汽车的摆放位置、顺序并无明确要求。在密集柜车库中，由于车库具有移动性，所以其刚度、强度弱于传统车库。汽车的存放和提取具有随机性，汽车可能全部集中在同一侧，导致车库进入整体结构不稳定的状态，如图10所示，其受力仿真分析如图11所示。可以看出，该状态下车库单元进行移动时容易对车轮的一侧造成额外的倾覆力矩，有严重的安全隐患。

图8 功能域分解

图9 结构域分解

图10 车辆不均匀摆放示意图

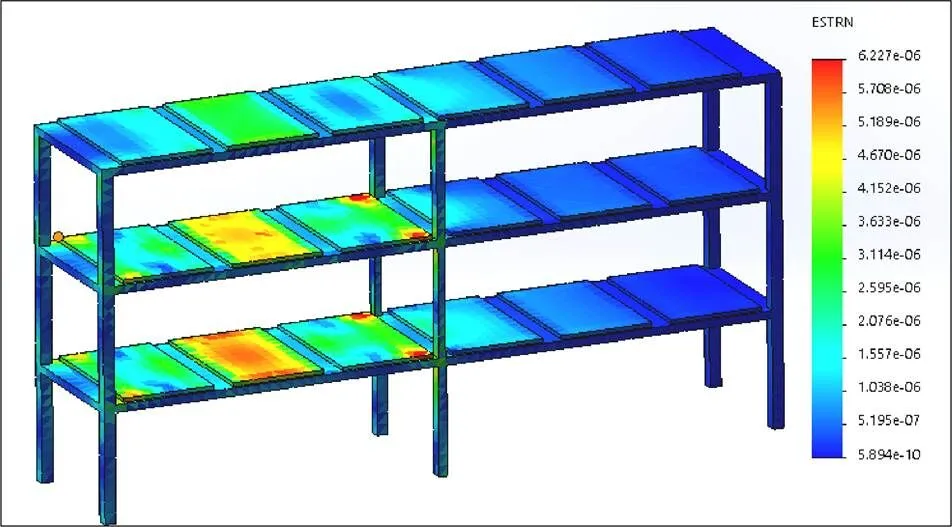
图11 不稳定状态的仿真分析

（3）从DCC的角度分析，车轮磨损过程属于2.1节所述的第一类偏差产生机理。其系统范围逐渐偏离设计范围，即任意时刻()都存在。所以此问题功能可以进行自愈设计。

（4）在设计之初设计放置算法，使车辆的存入方式更加科学，可避免车辆放置入同一侧的情况。但由于车主取车时的不确定性，此类车辆集中在一侧的情况仍不能完全避免。

通过上述有关自愈的分析可以看出，该问题不适合采用初始化自愈。对问题功能进行TRIZ转换。根据TRIZ工具中的技术冲突，将问题规范描述为：为消除车辆不均匀分布带来的结构不稳定情况，需要增加平衡配重块，并根据车辆分布情况，调节配重块的位置。这样将会导致装置更加复杂。应用技术冲突解决理论确定改善的参数为“可靠性”，恶化的参数为“装置的复杂性”。

通过查找冲突矩阵得到解决问题的发明原理，如表1所示。

表1 发明原理及注释

根据发明原理1，将车库每个列单元中的车位单元化，且增加移动能力，使其可以自行平衡车辆不均匀分布问题。用1表示。

建立功构映射的第三层设计矩阵为：

式中：1为夹放汽车；2为运送汽车；3为承载汽车；4为固定汽车；5为移动车位；6为监控车位；7为查询车位；1为夹放装置；2为移动装置；3为承载装置；4为固定装置；5为移动装置；6为监控装置；7为上位机系统。

设计矩阵为准耦合矩阵，通过改变设计顺序可以满足独立性公理。则有：

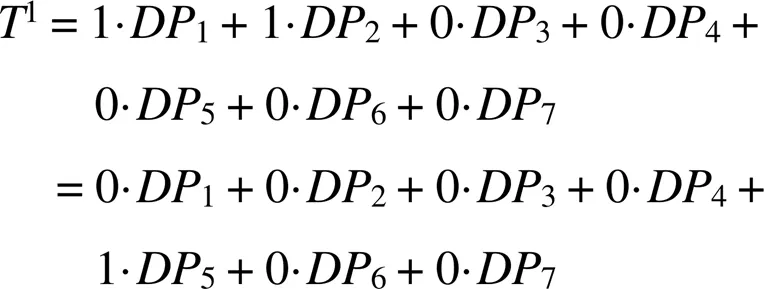
得出耦合关联矩阵为：

根据上述矩阵变换结果，可以认为，该问题可利用系统可用资源进行自愈设计，并且有两种耦合程度不相同的解法。第一种利用泊车装置的对车辆进行重新摆放，此过程会影响其他用户的使用。第二种解法是利用车库原有的内部驱动力进行车位移动，此方案需要通过连接结构传递动力。

选择第二种解法，在车库原有方案的基础上，通过对密集柜车库现有动力装置的复用添加了车位内部的运送装置，如图12所示。

图12 内部运送装置

通过该装置，可以在车库内部车辆摆放不合理时调整车辆的摆放方式，使系统更加稳定。添加装置后，车辆摆放方式如图13所示，其受力仿真分析如图14所示。

图13 调整后的摆放方式

图14 调整摆放方式后的仿真分析结果

由图14可知，该方案可以明显改善密集柜车库因车辆摆放不当导致的隐患，并能在系统运行过程中通过自愈的方式使系统保持稳定。

5 结论

对人工自愈理论、设计过程复杂性理论进行了研究，阐述了设计过程复杂性理论与人工自愈理论之间的联系及相似性。在自愈理论的基础上，结合现有设计过程复杂性与发明问题解决理论，提出一种自愈理念下的设计方法。通过分析现有理论和自愈理论的相似性，得出结合DCC的自愈思想，并在此基础上提出相应的过程模型，最后通过密集柜车库的设计验证了该方法的有效性。该方法表明，当系统中存在必然会出现并影响系统功能实现的问题时，可以采用自愈理念对系统进行设计，使系统可以更稳定持久地运行。

[1]高金吉. 人工自愈与机器自愈调控系统[J]. 机械工程学报，2018，54（8）：83-94.

[2]高金吉. 装备系统故障自愈原理研究[J]. 中国工程科学，2005（5）：43-48．

[3]王仲生，马世伟. 飞行器早期故障自愈方法及其应用[C]. 佛山：第六届全国信息获取与处理学术会议论文集，2008：233-235．

[4]黄立权，王维民，苏奕儒，等. 基于电磁自愈力的转子自动平衡方法与实验研究[J]. 振动与冲击，2011，30（1）：208-212.

[5]马晋，江志农，高金吉，等. 基于瞬时转速波动率的内燃机故障诊断方法研究[J]. 振动与冲击，2012，31（13）：119-124.

[6]姚剑飞，高金吉，王维民. 电磁力参数自寻优的转子多频振动主动抑制[J]. 振动与冲击，2015（18）：50-55.

[7]Yang D，Ni Y，Su H，et al. Hybrid energy system based on solar cell and self-recovery/self-cleaning triboelectric Nano generator[J]. Nano Energy，2021（79）：105394.

[8]Longbiao Huang，Xingyi Dai，Zhenhua Sun，et al. Environment- resisted Flexible High Performance Triboelectric Nano generators based on Ultrafast Self-recovery Non-drying Conductive Organ hydrogel[J]. Nano Energy，2021（80）：105724.

[9]Suh N P. Complexity：theory and applications[M]. New York：Oxford University Press，2005.

[10]Suh，Nam P. Complexity in engineering[J]. CIRP Annals - Manufacturing Technology，2005，54（2）：581-598.

[11]张鹏，冯浩，杨通达，等. 数字孪生与TRIZ集成迭代参数演化创新设计过程模型[J]. 计算机集成制造系统，2019，25（6）：1361-1370.

[12]高金吉. 人工自愈概论[J]. 机械工程学报，2021，57（2）：1-10.

[13]张鹏，杨伯军，张换高，等. 面向CAI的设计过程复杂性理论冲突确定原理[J]. 计算机集成制造系统，2013，19（2）：330-337.

[14] Suh N P，Lee T. Reduction of complexity of manufacturing systems through the creation of time-dependent combinatorial complexity[J]. CIRP Journal of Manufacturing Systems，2004，33（2）：87-100.

[15]张鹏，闫俊杰，王涛. 设计过程复杂性与TRIZ集成超声波纸张测厚装置创新设计[J]. 机械设计，2016，33（11）：26-29.

[16]张鹏，檀润华. 系统复杂性理想解快速获取方法[J]. 计算机集成制造系统，2010，16（4）：746-754.

[17]檀润华. TRIZ及应用[M]. 北京：高等教育出版社，2010.

[18]王慧欣，郑敏慧. 亮点纷呈稳健向前[N]. 中国交通报，2021- 07-22（006）.

Research on Design Method of DCC and TRIZ Integration under Self-recovery Concept

GUO Kun

( School of Mechanical Engineering, Hebei University of Technology, Tianjin300130, China )

In order to improve the stability of complex systems, the article introduces the concept of self-recovery into the conceptual design stage of complex systems and proposes a design method that integrates DCC (Design-Centric Complexity) and TRIZ (Theory of the Solution of Inventive Problems) by combining DCC and TRIZ based on the self-recovery concept. First, analyze the functions in the system and estimate the realization probability of the functions in the system through the DCC theory. Second, determine the potential problem functions with low realization probability, carry out the self-recovery design for these functions. After that, use the TRIZ tool to solve the problems. Finally, integrate above process to form a process model integrating DCC and TRIZ under the self-recovery concept, and the effectiveness of the process model is verified through a case of a dense cabinet garage.

self-recovery concept；design-centric complexity；TRIZ；concept design

TB472

A

10.3969/j.issn.1006-0316.2022.09.002

1006-0316 (2022) 09-0007-08

2021-08-02

郭昆（1994－），男，河北邯郸人，硕士研究生，主要研究方向为创新设计、机械工程，E-mail：394201178@qq.com。