考虑动态走行时间的铁路 换乘公交衔接优化

随着城镇化进程的深化，综合交通枢纽的作用和地位日益提升，乘客在枢纽内多种方式间的换乘效率直接影响到枢纽的协同运行效率、疏散安全和乘客体验，各方式的衔接优化也是当前学界关注和研究的重点[1]，以下重点研究枢纽内铁路到达客流换乘城市公交常见和普遍的换乘衔接问题。

综合客运枢纽的换乘衔接优化国内外已经有较为丰富的研究成果。Lee等[2]提出不同交通方式间可以通过设置“松弛时间”来实现换乘衔接的协调性，以成本最小为目标，松弛时间为决策变量建立换乘优化模型；Cheah等[3]提出将排队模型纳入大型设施建模，用于分析相关行人流；吕慎等[4]在实际调查数据的基础上，拟合乘客走行时间与通行距离之间的关系； 张发才[5]以乘客到达服从均匀分布为基础，建立了目标为乘客换乘等待时间最小的线性规划模型。分析上述研究成果可知，现有研究多将换乘走行时间假定为一常量，或者简单地通过数据拟合，建立与容量、走行速度相关的简单函数，但其准确性受到行人交通流基础数据不充分的制约，统计周期较长，而且基于以上假设的衔接优化模型未考虑列车到达时刻表等信息，仅考虑旅客均匀到达分布[6-7]，因而衔接优化研究仍有明显的空间。

排队论作为一种常见的交通系统建模方法已经得到了广泛的应用[8-17]，近年来，随着计算求解技术的发展，越来越多的学者利用流体排队模型和PH(phase-type)型排队模型开展交通系统复杂性、动态性、多尺度性的精细化研究。基于此，研究拟将枢纽内的铁路－公交换乘走行过程抽象成PH型流体排队模型，推导不同换乘客流状态下的乘客动态换乘走行时间，在此基础上，以乘客换乘等待时间成本与企业运营成本之和最小为目标，构建新的铁路到达客流换乘公交的衔接优化模型，以提升换乘衔接效果。

1 换乘走行时间推导与衔接优化建模

综合客运枢纽内旅客经过不同交通服务设施的换乘走行具体过程可以抽象为一个排队过程。以成都东站为例，铁路到站客流换乘城市公交的换乘过程可以描述为：铁路客流到达—站台—扶梯—出站检票闸机—换乘通道—扶梯—排队候车。

1.1 符号定义及基本假设

（1）符号定义。模型符号说明如表1所示。

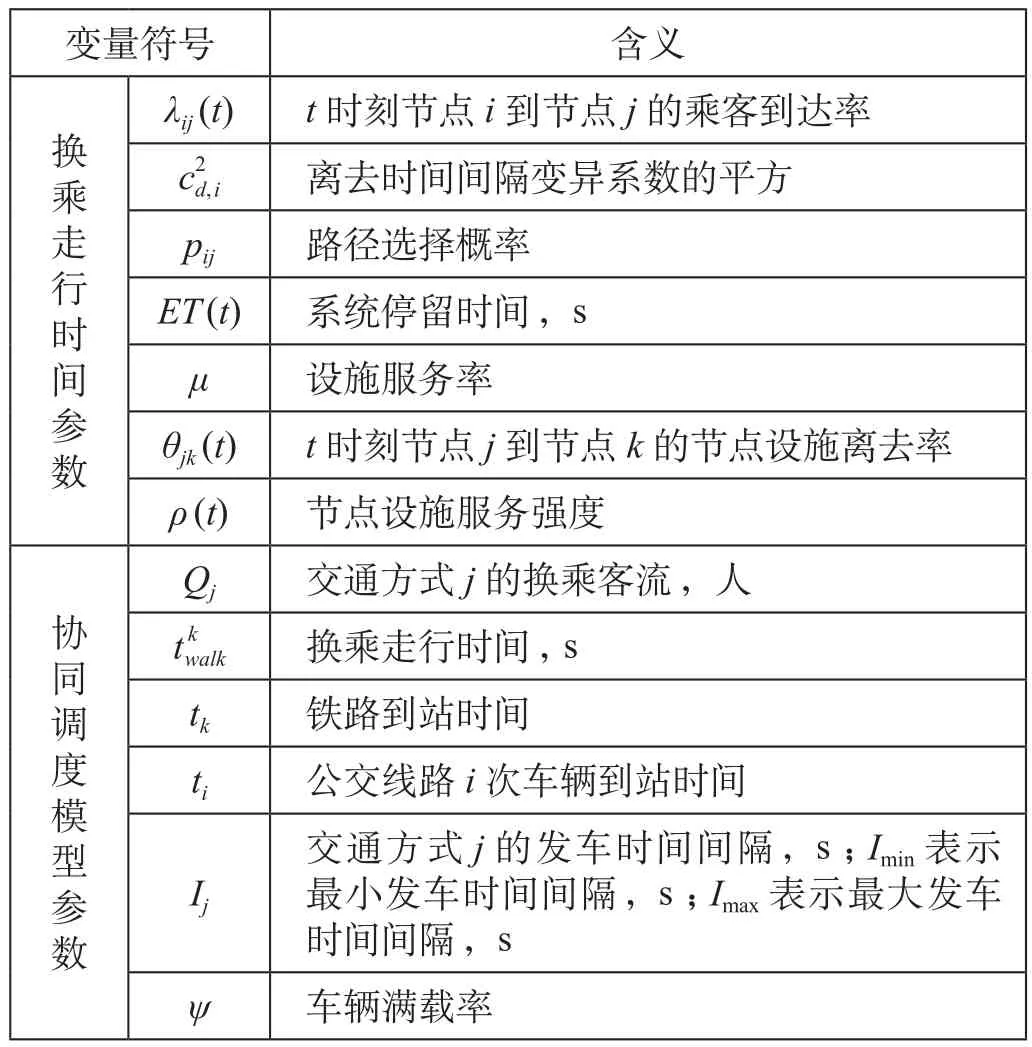
表1 模型符号说明Tab.1 Model symbol description

（2）基本假设。①研究时段换乘不同交通方式的换乘比例已知且固定。②各常规公交线路与铁路的换乘衔接独立考虑。③铁路准点到站，接运到站客流的公交的到站时间以铁路列车准点到站时间为基础。④换乘客流在接运站台遵循“先到先服务”的原则上车离开。⑤不考虑枢纽站衔接公交运营方案调整对整条线路客流的影响。

1.2 PH型流体换乘排队网络建模与换乘走行时间推导

客运枢纽内铁路到站客流换乘其他交通方式的排队网络图如图1所示。

图1 铁路到站客流换乘其他交通方式的排队网络图Fig.1 Queuing network of arrival passenger flow transfer from railway to other transportation modes

参考文献[14]至文献[17]，可将铁路旅客换乘其他方式的过程描述为一个PH型流体排队网络，具体过程中的关键参数分析如下。

（1）到站列车下车客流到达过程与到达率。作为系统输入流的铁路到站下车客流，通过历史数据可获得其时变到达率λ(t)以及到达间隔变异系数的平方ca2。

（2）节点设施的离去过程与离去率。节点设施i的离去率即为节点的输出率，参考文献[14]可以确定设施i离去时间间隔的变异系数平方c2d,i。

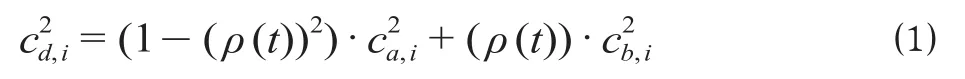
式中：c2a,i表示设施i乘客到达时间间隔变异系数的平方；c2b,i表示设施i服务时间变异系数的平方。

（3）设施间转移概率。假设节点设施间转移概率即为乘客路径选择概率pij，节点设施串联情况下，输入流与输出流相同，设施间转移概率pij= 1，若乘客从当前设施转移到多个并联设施时，根据转移客流量的不同，设施间转移概率将存在差异。为计算方便，研究应用统计的方法估算转移概率[6]，假设设施间转移概率固定，…，m，其中nij表示由节点设施i转移到节点设施j的次数。

（4）客流的合流与分流。基于以上分析，枢纽换乘过程由多个节点的合流与分流组成，在确定的概率转移基础上，建立整个换乘网络的换乘模型，客流的合并与分离如图2所示。

图2 客流的合并与分离Fig.2 Consolidation and separation of passenger flow

①客流的合并：将枢纽内节点设施的客流来源分为2类，枢纽外直接进入系统节点设施的客流；从上游并联或混联的节点设施转移到该节点设施的客流。客流的到达时间间隔符合〈λj(t)，c2a,j〉分布[13-14]。

式中：λj(t)表示客流到达率；λ0j(t)表示外部(记为节点0)到达客流的到达率；c2a,0j表示外部到达客流时间间隔变异系数的平方；c2a,j表示设施j乘客到达时间间隔变异系数的平方；c2d,ij表示由设施i到设施j客流离去时间间隔的变异系数的平方。当不考虑外部客流时，λ0j(t) = 0；当系统只有外部客流进入时，

②客流的分离：在换乘过程中，客流从一个设施节点转移到另一个设施节点，客流存在转移概率，而且不同设施间的转移概率可能不同，客流的离去时间间隔符合PH〈θjk(t)，c2d,jk〉分布[15]。

式中：θjk(t)表示从节点j到节点k的客流的离去率；表示从节点j到节点k客流离去时间间隔的变异系数的平方；θj(t)表示上一个节点设施j的离去率；pjk表示从节点设施j转移到节点设施k的选择概率；N表示换乘过程中总的节点数量，个。

铁路到站客流换乘公交的过程，由输入流的时间间隔、设施间的转移概率、各节点服务设施的服务时间、系统的排队规则等因素共同决定。由公式 ⑵、公式 ⑷ 可知，排队网络相较于单个节点设施，客流的到达时间间隔分布和离去时间间隔分布存在差异。铁路换乘公交的排队网络系统的输出率fout(t)。

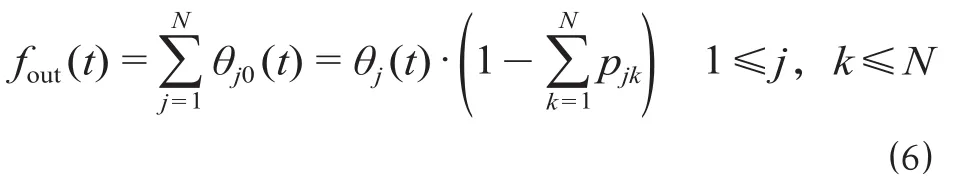
任意节点设施j的乘客停留时间ET(t)j可以表示为

式中：xj(t)表示t时刻设施j的系统状态；μj(t)表示设施j的服务率参数。

整个换乘过程的换乘走行时间tkwalk由各节点设施j的逗留时间ETj(t)、客流到达率λj(t)、铁路客流到达节点j的时变到达率λ0j(t)共同决定。

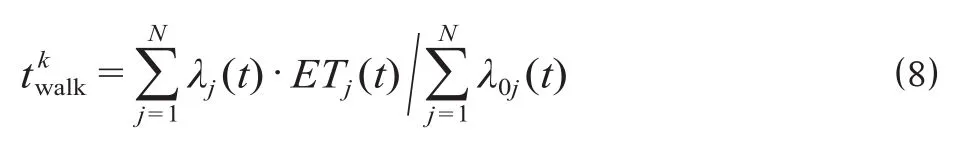
1.3 换乘衔接优化模型构建

以PH型流体换乘排队网络模型为基础，推导不同换乘客流状态下的乘客换乘走行时间，构建综合客运枢纽内旅客换乘公交的衔接优化模型如下。

式中：QB表示铁路到站客流换乘到常规公交的客流量，人；qki表示k班次到站旅客换乘到第i趟公交的换乘客流，人；ti表示第i趟公交的到站时刻；tk表示第k趟列车的到站时刻；α，β分别表示公交运营成本和乘客候车时间成本的权重系数；γ1表示单位公交运营成本，元；γ2表示换乘公交乘客的平均候车成本，为全市平均工资水平W与工作时间D的比值；NBl表示研究时段内发送的公交车辆总数，辆。

（1）运能匹配性约束。

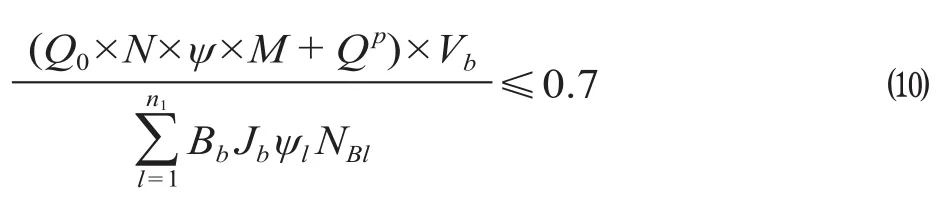
式中：Bb为标准车型公交的载客人数，人；Jb为车辆换算系数；ψl为公交的满载率；Q0表示列车每节标准车厢的额定载客数，人；N表示列车的车厢数，辆；ψ表示列车的满载率；M表示研究时间内终到站的列车数，列；Qp表示途经列车的出站客流，人；Vb表示公交换乘比例。

（2）发车时间约束。考虑到线路中间站点乘客的乘车需求，公交发车时间间隔不宜过大，同时为减少运营公司成本，发车时间间隔不宜太小。调整公交发车时间间隔在一定范围内波动，有效接续铁路到站客流的同时，不影响线路中间站点乘客的乘车需求。

（3）公交计划发车约束。公交计划到达换乘站点时刻在研究时间T内，研究时间T内公交运营车次不多于现有运营方案车次X的1.5倍。

（4）换乘等待时间约束。到达站台的乘客均能搭乘最近一班公交车离开站台，换言之，单个乘客的换乘等待时间小于公交的发车时间间隔。

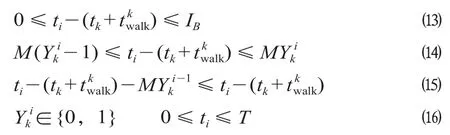
公式 ⒀ 至 ⒂ 共同保证铁路到站客流可以换乘到最近的一班公交离开系统，Yki为0-1变量，当铁路线路k的到站旅客能换乘到公交线路l最近一班车次i时，Yk i= 1，否则Yki= 0，M为一个足够大的已知正数。

2 算法设计

首先固定点迭代算法求解系统状态x(t)，然后带入公式 ⑺、公式 ⑻ 求解整个换乘过程的换乘走行时间tkwalk。

步骤1：初始化排队系统。设置初始时间t0，时间步长Δ，系统初始状态x(0)，最大时间节点tmax，系统服务强度的初始值ρ(0)。

步骤2：模型构建及相关参数输入。换乘排队系统的构建，乘客到达率λ(t)、各节点设施的服务率μ(t)、设施间选择概率pjk等相关参数的输入。

步骤3：动态排队系统的迭代求解。确定时间步长，运用固定点迭代算法求解系统状态x(t) =μ(t-1)-μ·ρ(t-1)·Δ +λ(t-1)·Δ，然后求解系统的输出率fout(t) =θj(t)·

步骤4：换乘网络乘客系统停留时间的计算。将步骤3求解的x(t)以及对应状态下的设施服务率μ(t)带入公式 ⑺ 中，求解时间t内，在换乘公交的乘客数确定的情况下，乘客在换乘排队网络系统中的逗留时间

然后，将换乘走行时间代入换乘优化模型中，利用遗传算法进行求解。

3 成都东站铁路-公交换乘优化实例分析

成都东站作为国内六大枢纽客运站之一，集铁路、公交、地铁、出租车、长途旅游客运以及社会停车场等功能于一体，共设有5层。铁路到站旅客在地下一层通过出站闸机后经换乘大厅换乘市内公交，无需出站。

3.1 成都东站铁路换乘公交的网络建模

对成都东站铁路换乘公交的主要换乘流线进行抽象，得到铁路换乘公交排队系统如图3所示。

图3 铁路换乘公交排队系统Fig.3 Queuing system of railway transfer to bus

根据现场调查及参考文献[6-7]，设施间转移概率为p0,1=p0,3= 0.4，p0,2=p0,4= 0.1，p1,5=p3,6= 0.4，p2,5=p4,6= 0.1，p5,7=p6,7= 0.5，p7,9= 0.1，p7,8= 0.9，p8,10= 0.9，p9,10= 0.1。根据文献[18]，确定企业和乘客换乘等待时间的权重系数组合为 (0.5，0.5)。

研究时段内铁路到站下客列车共14列，到站客流约5 776人，基于实际调查数据确定到站客流换乘不同交通方式的分担率，其中换乘常规公交的比例为0.18。根据参考文献[18]，确定公交车辆运营成本50元/车，换乘客流时间成本0.28元/ (min· 人)。

3.2 计算结果分析

根据前述算法，输入乘客到达率λ(t)、各节点设施的服务率μ(x)、设施间选择概率pjk等相关参数，得到优化前三类公交到站时刻表如表2所示。将换乘走行时间及相关约束变量代入公式 ⑼，利用遗传算法求解其衔接优化方案及最小目标函数，算法优化结果收敛图如图4所示，优化后公交到站时刻表如表3所示，优化前后相关数据对比表如表4所示。

表3 优化后公交到站时刻表Tab.3 Optimized bus arrival timetable

表4 优化前后相关数据对比表Tab.4 Comparison of results before and after optimization

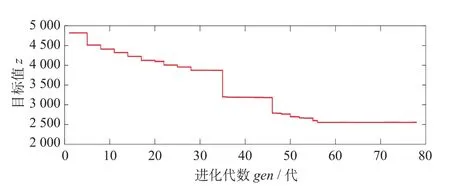
图4 算法优化结果收敛图Fig.4 Convergence process of algorithm optimization

表2 优化前三类公交到站时刻表Tab.2 Three types of bus arrival timetables before optimization

优化前公交以等间隔发车，存在公交刚刚离开站台，换乘客流便到达站台的现象，导致换乘等待时间较大；优化后公交发车时刻与换乘客流到站时刻相协调，使得铁路到站客流换乘等待时间相对更小，且不存在公交刚发车离站换乘客流便大量到达站台情况。

综上，通过协调公交到站时间，减小了乘客换乘等待时间，优化后换乘公交的系统成本为225.2，相较于现有运行方案，系统成本减少了31%，乘客平均换乘等待时间约减少了62%。通过优化接驳公交的到站时刻，减少了公交换乘系统的目标函数值，同时减少了单位时间乘客的换乘等待时间，验证了模型的有效性。

4 结束语

通过建立PH型流体换乘排队网络模型，基于不同换乘客流状态下的乘客换乘走行时间，对综合客运枢纽内铁路到达旅客换乘公交的换乘衔接进行优化设计，实例分析表明：研究提出的换乘优化方法可显著减少乘客换乘等待时间，降低换乘公交的系统成本，可用于指导铁路枢纽内铁路换乘公交系统的精细化设计，提高设计质量。研究主要考虑了铁路和常规公交的换乘场景，但方法的优化思路同样可借鉴用于铁路枢纽内其他交通方式之间的换乘优化设计，提高枢纽内多模式换乘系统的效率，降低换乘系统的建设成本。