基于修正牛顿-拉普森迭代的数值流形法

张亚军，莫思阳，张友良

(海南大学土木建筑工程学院，海南 海口 570228)

1 引言

数值流形法[1，2]是石根华博士以数学流形为基础，利用有限覆盖技术建立起来的一种新型数值方法。该方法可以统一处理连续问题和非连续问题，分析小变形开裂和非连续大位移状态并模拟运动全过程。有限元法(FEM)和非连续变形分析法(DDA)都是数值流形法的特例。该方法提出后，已广泛应用于许多岩土工程实际领域，如裂隙扩展[3-6]、洞室开挖[7-9]、渗流[10-12]等。

数值流形法最初开发建立在线弹性假设基础上。聂治豹等[13]将数值流形法与边界元法进行耦合，提出了一种具有边界积分形式的数值流形法来进行二维弹性静力问题研究。徐栋栋等[14]在物理覆盖位移函数中增加一种新的局部位移函数，在不增加自由度的基础上克服了线性问题，并通过均质边坡弹性力学算例进行了有效性验证。骆少明等[15]采用规则的六面体数学网格建立三维数值流形有限覆盖系统，对三维数值流形法进行了理论推导等研究，建立了线弹性变形三维数值流形分析的理论体系。上述数值流形方法多基于线性本构关系，而实际岩土体结构具有材料和几何双重非线性的特性需要进行弹塑性分析。目前对于非线性问题(如弹塑性问题等)的研究还比较少[16，17]，因此，发展非线性数值流形法是必要的。由于牛顿-拉普森法多用于非线性求解中，同时也可以和其它非线性求解方法联合使用。王军祥等[18]将Newton-Raphson法与Arc-Length法相结合，用来求解针对岩石弹塑性阶段发生的应变软化等问题。贾硕等[19]将Woodbury公式引入局部非线性分析中，提高了矩阵求逆的效率，在此基础上利用N-R法和其它方法求解具体算例钢框架和薄钢板，并分析了相应求解方法对应的计算误差、时间复杂度以及收敛快慢程度等方面。但是将Newton-Raphson迭代法应用于数值流形非线性问题求解的方面尚未发现相关研究工作。

针对上述问题，本文尝试将牛顿-拉普森迭代法和数值流形法相结合来分析材料非线性问题，提出了基于修正牛顿-拉普森迭代的数值流形法。在迭代求解过程中只需在初始迭代步建立刚度矩阵，此后迭代步沿用，可降低求解大型工程问题过程的耗时，提升了非线性求解的效率。

2 NMM覆盖位移函数

整体位移函数由定义在各个物理覆盖上的覆盖位移函数通过权函数连接形成。定义在物理覆盖Ui上的覆盖函数ui(x，y)和vi(x，y)一般级数形式为

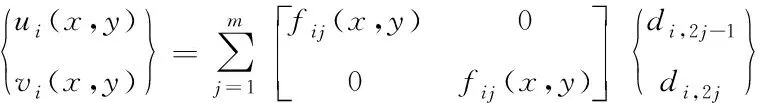
(1)

其中，fij(x，y)为多项式的基本级数；di，2j-1，di，2j为物理覆盖的自由度，是级数每项系数对应的未知量。覆盖函数阶数可取0阶到高阶，对应于0，1，2阶，m分别为1，3，6。

覆盖函数为0阶时，其常量函数形式为

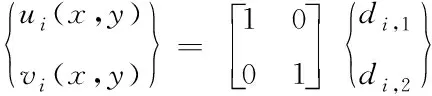
(2)

物理覆盖的每一个交集定义为流形单元，流形单元是物理覆盖的再剖分。若流形单元e是q个物理覆盖Ue(1)，Ue(2)，…，Ue(q)的交集，每个物理覆盖上的权函数为we(r)(x，y)，则单元e的整体位移函数为

(3)

将式(1)代入式(3)右侧，可得到以变形矩阵Tij(x，y)表达的整体位移函数为

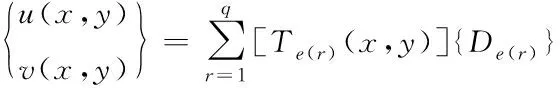
(4)

(5)

(6)

其中，{De(r)}为物理覆盖的自由度，为2m阶向量。

3 修正牛顿-拉普森迭代方法

考虑非线性时，材料的应力-应变关系不再满足胡克定律，其刚度矩阵不是一个常数，而与应变和位移值有关。此时，结构刚度方程是一个非线性方程组

[K]{u}={Fext}

(7)

其中，[K]为刚度矩阵；{u}为节点位移向量；{Fext}为节点荷载向量。

求解非线性方程组的方法包括增量法和迭代法。其中，增量法又分为始点增量法和中点增量法。

增量法的原理是把计算过程分为几个荷载增量步，增量步可以等分，也可以不等分。假定每个荷载增量步内的方程是线性的，在该增量步内的刚度矩阵[K]为常数，不同增量步的刚度矩阵[K]可以不同。每加载一个荷载增量{ΔFext}，得到该增量所对应的位移增量{Δui}，将所有荷载增量步的位移增量进行叠加，得到总位移{u}。

而利用迭代法求解方程组时，不需划分荷载步，一次施加全部荷载，然后逐步调整位移值，使得式(7)的变形式(8)得到满足。

[K]{u}-{Fext}=0

(8)

牛顿-拉普森迭代法是一种在实数域和复数域上求解方程的方法，它迫使解在每个荷载增量末端达到一定容许范围内的平衡收敛，可有效解决荷载增量法中因误差积累导致解发散的问题。由于具有收敛性好，形成方程数量少，计算速度快的特点，牛顿-拉普森迭代法被广泛应用于非线性方程组的求解中。

流形单元刚度矩阵为

[Ke(r)e(s)]=∬[Be(r)]T[Depc][Be(s)]

(9)

其中，[Be(r)]，[Be(s)]均为流形元应变矩阵；[Depc]为一致切线模量矩阵；采用四边形数学网格时，r，s=1，2，3，4。则

(10)

修正牛顿法在传统牛顿法基础上做了改进。如图1所示，若采用传统的牛顿-拉普森迭代法，刚度矩阵应在每个迭代步中根据非一致切线模量矩阵[Dep]建立，传统牛顿法的缺点在于刚度矩阵需要在每个迭代步中重新形成并求逆，在求解大型问题时尤其费时，且刚度矩阵求逆时可能会出现奇异或病态的问题。修正牛顿-拉普森迭代方法则可以克服以上困难，只需要在初始迭代步时建立刚度矩阵并求逆，此后的迭代步即可沿用初始迭代步的刚度矩阵，如图2所示。相比于牛顿法，修正牛顿法虽然降低了迭代的收敛速度，却大大节省了计算时间。本文采用修正牛顿-拉普森迭代法进行分析计算。

修正的牛顿-拉普森迭代可以表达为下列方程

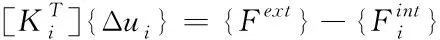
(11)

{ui+1}={ui}+{Δui}

(12)

使用修正牛顿-拉普森迭代法分析非线性问题的流程为：

1)确定初始位移{ui}。修正牛顿-拉普森迭代是一种梯度迭代算法，初始值的确定对算法的收敛速度有重要影响。在初始迭代步，{u0}={0}；

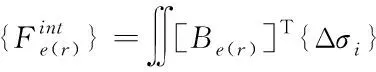
(13)

{Δσi}={σi}-{σi-1}

(14)

其中，{Δσi}为当前迭代步单元应力{σi}与上一迭代步单元应力{σi-1}之间的差值。当前迭代步和上一迭代步的应力计算均与选取的本构模型有关，具体过程在第3节论述。

5)利用式(12)计算下一迭代步更新后的位移向量{ui+1}，同时作为下一迭代步的初始位移值；

6)重复过程2)～5)，直至不平衡力小于一定范围时，认为结果收敛，迭代结束。

4 摩尔-库仑模型在NMM中的应用

土是一种很复杂的材料，土的本构关系受到诸多因素的影响，如密度、含水量、应力历史等。已提出的土的本构模型包括线弹性模型、非线性模型、弹塑性模型等[20，21]。

摩尔-库仑模型属于弹塑性模型，主要用于描述岩土介质的抗剪破坏行为，适用于模拟一般岩土体的力学行为，如边坡稳定和地下开挖等。

本构模型不同，迭代步内的应力算法则相应不同。以摩尔-库仑模型为例，其应力算法为隐式返回映射算法[22]。具体计算流程如下：

1)预测单元弹性应力并求主应力

根据已知的单元B矩阵和位移值求得单元应变，进一步按弹性方法求出单元应力作为预测应力值，在主应力方向分解后得到主应力。

2)检查应力是否进入塑性状态

若满足式(15)，说明流形元尚处于弹性状态，则可将第1)步所求预测单元弹性应力作为实际应力值。若不满足式(15)，则进入第3)步。

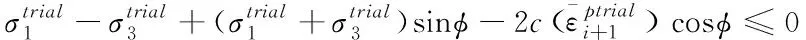
(15)

(16)

3)返回映射。

存在以下三种返回映射类型，按顺序依次进行：①返回至主平面；②返回至棱边(右或左)；③返回至顶点。在执行当前返回映射类型后根据式(17) 检查应力结果的有效性，若有效，则直接进入第4)步，若检查为无效，则执行下一类型的映射。

σ1≥σ2≥σ3

(17)

4)组装应力张量并更新弹性应变。

5 算例

该算例引用自文献[23]，计算模型如图3所示。计算模型约束条件为：边坡底边AB受双向固定约束；垂直侧边AF和BC受x向固定约束，y向自由。采用四边形数学网格对其进行网格划分，则形成如图4所示的流形元覆盖系统，共141个物理覆盖，114个流形单元。弹性模量E为100000000 N/m2，泊松比ν为0.35，重度γ为20000 N/m3。摩尔库仑模型各参数见表1。

表1 材料参数

根据有限元求解理论，剪胀角为5度下安全系数为1.09。根据上述提出的求解方法，求解时采用0阶覆盖函数，利用修正牛顿-拉普森迭代法对该边坡算例进行非线性分析，并将程序得到的计算结果与有限元理论值进行比较，对比结果如表2所示。

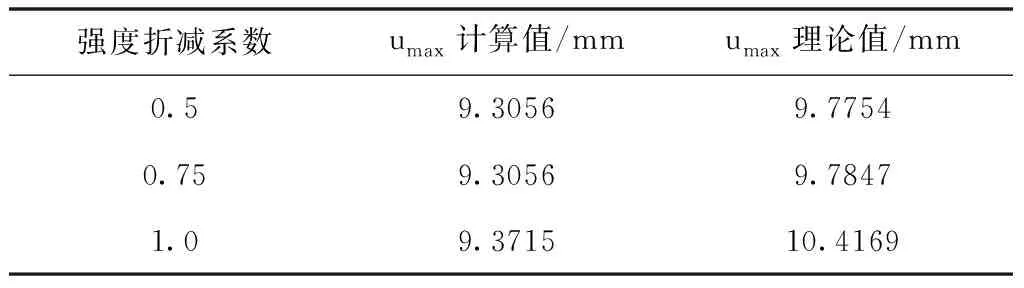
表2 umax计算值与理论值

从上述结果可以看出，计算结果与算例有限元理论值比较吻合，说明利用修正牛顿-拉普森迭代法求解材料非线性问题是可行的。

6 结论

为了推进数值流形法在材料非线性方面的应用，据此将牛顿-拉普森引入到数值流形法中，提出一种可以求解非线性的修正牛顿-拉普森迭代的数值流形法。首先采用摩尔-库仑本构模型，求解材料非线性问题，内外力差满足收敛容许值即收敛，以力为基础的收敛提供了收敛的绝对量度；其次牛顿-拉普森迭代迫使计算结果在每个计算步的末端达到平衡，相比于常见的荷载增量法，可避免荷载增量过程中误差积累而导致结果失去平衡的问题；最后由于每个计算步中的弹性矩阵假设为常数矩阵，则该方法可求解任意阶数的数值流形问题。通过算例验证了该方法的可行性，为数值流形法在非线性领域的应用奠定理论基础。