多端混合直流输电系统谐波传递特性及交互影响

顾广坤，李海锋，梁远升，邓成江，王钢

(1.华南理工大学 电力学院，广东 广州 510641；2.南方电网超高压输电公司广州局，广东 广州510663)

基于晶闸管相控换流器的传统高压直流输电(line commutated converter high voltage direct current，LCC-HVDC)技术的研究和应用已非常成熟。然而，LCC存在逆变侧换相失败、无法实现无源运行等缺陷，限制其进一步发展。相较于LCC，模块化多电平换流器(modular multilevel converter，MMC)具有控制灵活、模块化设计等优点，但存在建设成本高、运行损耗大等缺点。因此，综合LCC和MMC技术的混合直流输电系统开始得到广泛关注，并得到了工程应用[1-3]。

混合直流系统正常稳态运行时，12脉LCC向直流回路注入12k(k=1，2，…)次特征谐波，成为系统的主要谐波源。而在各种非理想因素(如交流系统存在背景谐波、三相不平衡以及调制方式等)的影响下，系统还将产生额外的非特征谐波[4-5]，从而引发一系列问题，如交直流系统保护误动[6]、系统发生谐振[7-8], 谐波不稳定等[9-10]。系统稳态运行时非特征谐波并不明显，但可能在某种条件下发生谐振，使其明显放大。因此，有必要对直流输电系统的谐波传递特性以及交互影响进行研究，分析各元素对谐波传递和交互作用的影响。这不仅可以明确系统运行的风险，还可为系统谐波抑制技术等提供理论支撑。

目前，许多文献分析了由同一类型换流变电站(以下简称“换流站”)组成的双端直流输电系统[11-12]及多端直流输电系统[4,13]的谐波产生机理，表明不同换流站之间存在复杂的谐波交互作用。近年来，已有一些文献对双端混合直流输电系统直流侧谐波电流计算方法[14]以及直流回路谐振特性[15]进行了研究。由于多端混合直流输电系统是由不同类型换流站组成，LCC与MMC之间以及不同的MMC之间对直流系统产生的谐波并不独立，导致换流站与直流系统之间的谐波交互情况远比单一的LCC/MMC直流输电系统以及LCC-MMC双端混合直流输电系统复杂。

为此，本文首先建立LCC、MMC的直流侧等值谐波阻抗模型、直流输电线路的谐波模型，在此基础上得到多端混合直流输电系统的直流侧谐波阻抗模型。随后，形成系统的节点阻抗矩阵，通过分析其中各元素的频率特性，得到系统的谐波传递特性以及各次谐波在不同换流站间的交互影响。接着，分析直流输电线路长度、换流变压器(以下简称“换流变”)换相阻抗、整流侧平波电抗器的改变对多端混合直流输电系统谐波传递特性的影响。最后，在PSCAD/EMTDC中搭建仿真模型，验证本文所提谐波分析方法的正确性。

1 多端混合直流输电系统直流侧等值谐波阻抗模型

图1 多端混合直流输电系统拓扑结构

1.1 LCC直流侧等值谐波阻抗模型

在直流谐波研究中，LCC等值一般采用3脉动模型[16]，从直流侧看进去，交流系统阻抗和交流滤波器可等效为并联回路引入到换流器3脉动模型中间[17]。因此考虑交流系统和交流滤波器时，每个6脉动换流器等效模型如图2所示，其中：Cp为换流变压器对地杂散电容, 一般为10～20 nF；Z3p为换相阻抗。

图2 含交流系统和交流滤波器的6脉动换流器模型

对于换流变压器变比为K，且由n台6脉动换流器组成的换流站，其等效到直流侧的换相阻抗Z3p、交流系统阻抗Zdc_ac、交流滤波器阻抗Zdc_acf分别为[18-19]：

(1)

式中：ω0为系统工频角速度；ω为系统角速度；Zc为6脉动换流器的换相阻抗；μ为换流器换相角。式(1)的推导基于开关函数理论[20]，推导过程中忽略了开关函数的谐波分量，仅取其基波分量进行近似计算，所得等值模型适用于系统稳态或者发生小扰动情况下的谐波分析。

1.2 MMC直流侧等值谐波阻抗模型

MMC直流侧电压回路方程为[4]

(2)

式中：L0和R0分别为桥臂电感和桥臂等效电阻；j=a,b,c，表示三相符号；ucomj=(upj+unj)/2为上下桥臂共模电压，icirj=(ipj+inj)/2为相环流，upj、ipj和unj、inj分别为上、下桥臂的电压、电流；udc为直流电压。

由式(2)可得MMC直流h次电压谐波

(3)

式中：C为一相等效电容；idc(h)为直流h次电流谐波。分析MMC谐波传递特性时，忽略控制策略的影响以及桥臂内部动态，认为子模块电容电压为恒定值，在上、下桥投入子模块数量之和恒定为N的前提下，每相上、下桥臂可等效为一个电容C=2C0/N。可得MMC直流侧等值谐波阻抗[7,21]

(4)

式中：C0为MMC子模块电容；f为频率。MMC直流侧谐波阻抗可等效为图3所示的RLC串联结构形式。

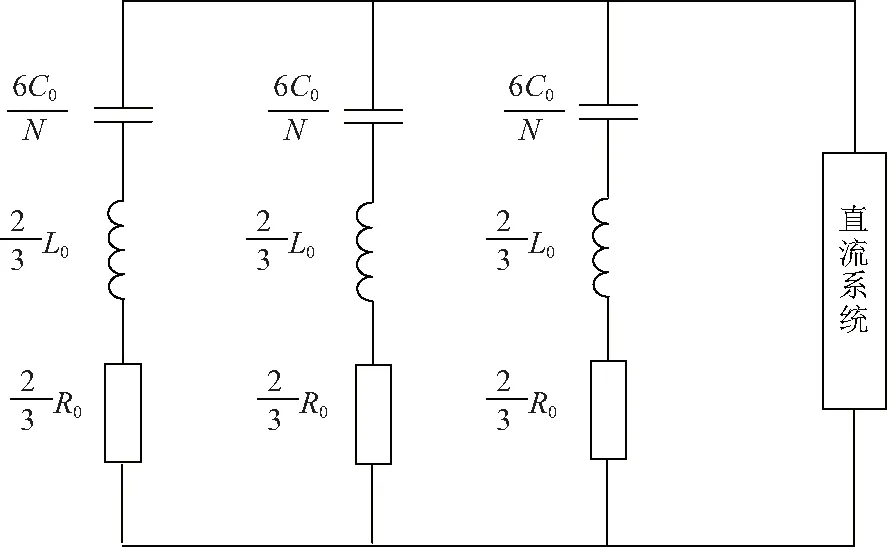
图3 MMC直流侧等值谐波阻抗模型

1.3 直流输电线路的谐波模型

进行谐波分析时，可采用考虑分布参数效应的π型等值模型，如图4所示[13]。

图4 输电线路模型

在h次谐波下，线路的等效串联阻抗为Zeq(h)，等效并联导纳为Yeq(h)，表达式分别为

(5)

(6)

式中：L为输电线路长度；Zs和γ分别为直流输电线路的波阻抗和传播常数；考虑到线路的频变特性，z(h)、y(h)分别取为h次谐波下线路单位长度的串联阻抗及并联导纳。

1.4 多端混合直流输电系统直流侧谐波阻抗模型

由上述等值模型可以得到多端混合直流输电系统的等值电路如图5所示。图5中：Z1、Z3分别为直流输电线路L1、L3的等效串联阻抗；Y1、Y3分别为直流输电线路L1、L3的等效并联导纳。

图5 多端混合直流输电系统直流侧谐波阻抗模型

根据图5所示的等值电路，可得系统的节点阻抗矩阵

(7)

(8)

式中：Zii(f)为换流站i的自阻抗,i∈{1,2,3}，反映了换流站i直流侧等效电流源对自身换流站直流侧端口电压的作用；Zij(f)为换流站i对换流站j的转移阻抗(i≠j)，反映了换流站j直流侧等效电流源对远端换流站i直流侧端口电压的作用。

谐波阻抗与各换流站谐波传递关系如图6所示。

图6 谐波阻抗与各换流站谐波传递关系

在谐波电流幅值相同的情况下，谐波自阻抗和转移谐波阻抗值越大，换流站直流侧产生的谐波电压就越大，即谐波电流对换流站的影响越大。

将谐波电流在远端换流站引发的谐波电压畸变值与本站的谐波电压畸变值进行比较，定义谐波电压传递系数[22]

(9)

当μij(f)的幅值小于1时，发生谐波电压传递衰减现象；当μij(f)幅值大于1时，发生谐波电压传递放大现象。

2 多端混合直流输电系统谐波传递作用分析

2.1 多端混合直流输电系统谐波传递特性分析

根据1.4节建立的谐波阻抗模型，以MMC1、LCC直流侧含有谐波电流为例，分析谐波在MMC与LCC之间、MMC与MMC之间的谐波传递特性。给定系统的参数见表1，其中，该系统直流输电线路1和线路3长度均为200 km。

表1 多端混合直流输电系统电路参数

2.1.1 谐波阻抗计算

谐波阻抗计算结果如图7所示，由图7(a)可见，Z11(f)、Z31(f)的谐振点在450 Hz附近，表明当MMC1直流侧含450 Hz谐波电流时，MMC1、LCC的直流端口电压均会发生谐振，且Z11(f)>Z31(f)。除了500 Hz的各次谐波，Z11(f)比Z21(f)、Z31(f)大，说明当MMC1直流侧含有除500 Hz外的谐波电流时，对本站直流端口电压的影响程度比远端换流站更大。

由图7(b)可见，Z33(f)的谐振点在150 Hz附近，表明LCC直流侧含150 Hz谐波电流时，LCC的直流端口电压发生谐振。Z13(f)、Z23(f)的谐振点在450 Hz附近，表明LCC直流侧含450 Hz谐波电流时，MMC1、MMC2直流端口电压发生谐振。

图7 谐波自阻抗和转移谐波阻抗幅频曲线

LCC谐波自阻抗Z33(f)的幅值比MMC1谐波自阻抗Z11(f)的幅值大，表明与LCC相比，MMC抑制本站谐波电流能力更强。

2.1.2 谐波传递系数计算

谐波传递系数计算结果如图8所示。以500 Hz为例，此时μ21(f)=1.517>1，μ31(f)=0.492<1，表明当MMC1直流侧含有500 Hz的谐波电流源时，MMC2直流侧500 Hz谐波电压幅值将是MMC1的1.517倍，LCC直流侧500 Hz谐波电压幅值将是MMC1的0.492倍，MMC1的500 Hz谐波向MMC2传递时会发生谐波电压传递放大现象，向LCC传递时会发生谐波电压传递衰减现象。对于除了500 Hz的各次谐波，μ21(f)<1、μ31(f)<1，说明除了500 Hz的各次谐波在MMC1向LCC、MMC2传递时存在谐波电压传递衰减现象。

图8 多端混合直流输电系统谐波传递系数幅频曲线

对于各次谐波，μ13(f)<1、μ23(f)<1，说明各次谐波在LCC向MMC1、MMC2传递时存在谐波电压传递衰减现象。

2.2 多端混合直流输电系统谐波传递特性影响因素分析

2.2.1 直流输电线路长度

改变MMC1出口直流输电线路L1的长度l1，得到不同直流线路长度下的MMC1对MMC2的转移谐波阻抗Z21(f)、LCC对MMC1的转移谐波阻抗Z13(f)的幅频特性曲线，如图9所示。

由图9可见，当直流输电线路长度变化时，Z21(f)、Z13(f)的谐振频率和谐振幅值均发生了变化，在中高频段，Z21(f)、Z13(f)幅频特性幅值随线路长度的增大而减小。

图9 直流输电线路对谐波传递特性影响

2.2.2 换流变压器换相阻抗

改变换流变压器换相阻抗xt(标幺值)，得到不同换相阻抗下的Z21(f)、Z13(f)的幅频特性曲线，如图10所示。

图10 换流变压器换相阻抗对谐波传递特性影响

由图10可见，换流变换相阻抗的变化不会影响Z21(f)、Z13(f)的谐振频率，但Z13(f)幅频特性幅值随换流变换相电抗的增大而明显增大，而Z21(f)幅频特性幅值受其影响很小。因此可通过减小LCC换流变换相电抗值实现谐波的抑制。

2.2.3 整流侧平波电抗

改变整流侧平波电抗的大小，得到不同平波电抗值下的Z21(f)、Z13(f)幅频特性曲线如图11所示。

图11 整流侧平波电抗对谐波传递特性影响

由图11可见，整流侧平波电抗的变化不会影响Z21(f)、Z13(f)的谐振频率，但Z13(f)幅频特性幅值随整流侧平波电抗的增大而明显减小，而Z21(f)幅频特性幅值受其影响较小。因此可通过增大整流侧平波电抗值实现谐波的抑制。

3 仿真验证

为对多端混合直流输电系统的谐波传递特性进行验证，在PSCAD中搭建LCC-MMC-MMC并联型三端混合直流输电系统仿真模型，参数与表1相同。

3.1 换流器直流侧等值谐波阻抗模型验证

为验证上述直流侧谐波等效阻抗模型的正确性，分别采用解析计算法和测试信号法，对LCC、MMC1、MMC2直流侧谐波阻抗特性展开分析，部分结果如图12所示。由图12可知：LCC直流侧谐波阻抗计算结果与仿真结果在较宽的频段范围内基本吻合；定电压控制的MMC1与定功率控制的MMC2直流侧谐波阻抗计算结果与仿真结果在100 Hz以下部分频段存在差异〔这是由于MMC直流侧容性阶段阻抗(100 Hz 以下)受到控制模式的影响[23]〕，但在较高频段(100 Hz以上)的准确度较高。这表明本文所采取的换流器直流侧谐波等效阻抗的解析等值模型是合理的。

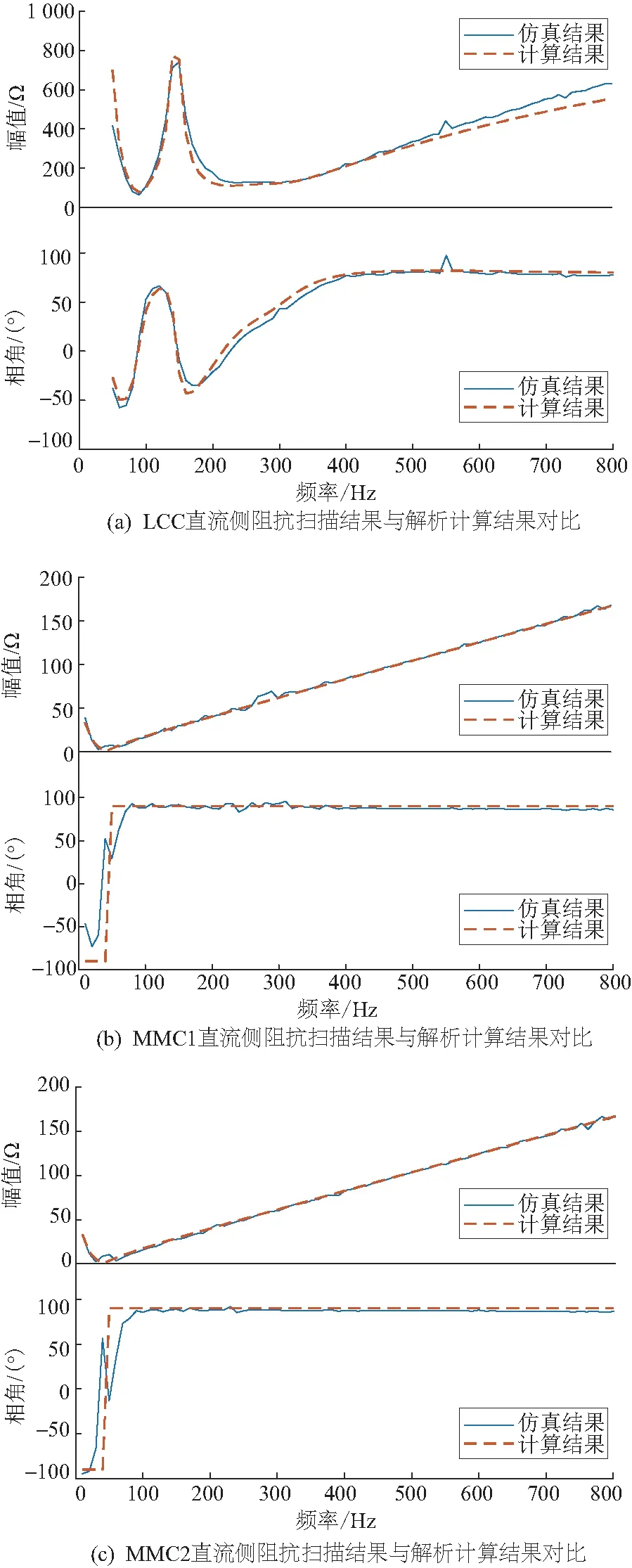
图12 换流器直流侧谐波阻抗频率特性

3.2 多端混合直流输电系统谐波交互影响分析

根据谐波等值阻抗计算得到的谐波传递系数μ21和μ13见表2。

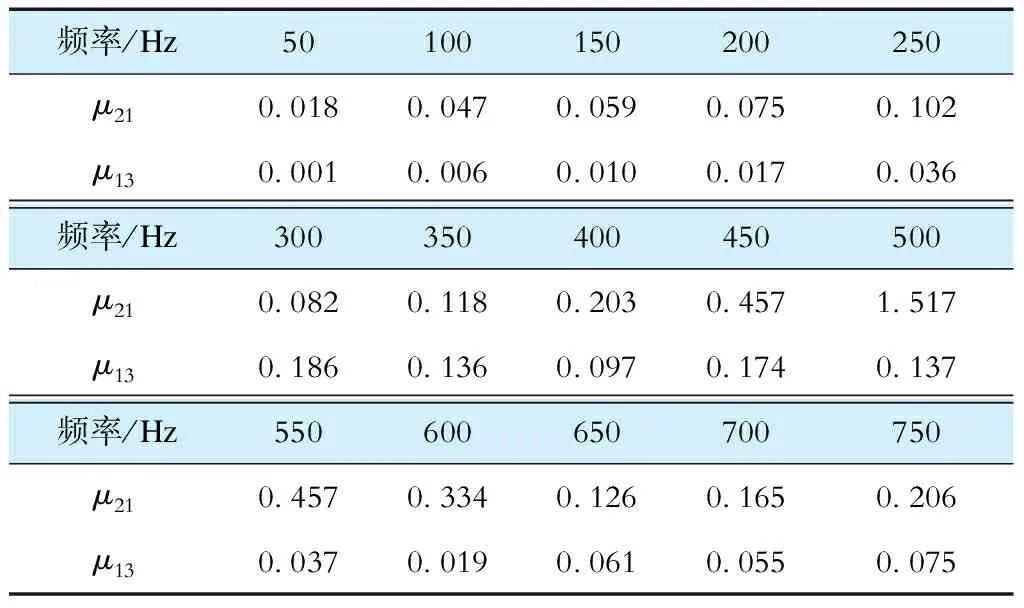
表2 谐波传递系数μ21和μ13的计算值

根据LCC交直流谐波传递规律可知，当LCC交流侧电压含有5次正序背景谐波时，其直流侧将产生4次谐波分量，得到的MMC1和LCC 直流端口电压频谱分析如图13 所示。

由图13可知，当LCC交流侧含5次正序背景谐波，LCC直流侧4次电压谐波为28.53 kV，传递到MMC1直流侧时，其4次电压谐波衰减为0.52 kV。此时可以得到谐波传递系数μ13的仿真值为0.018，与计算值0.017基本吻合。

图13 LCC交流侧含5次正序背景谐波时LCC和MMC1直流侧电压频谱分析

根据MMC交直流谐波传递规律可知，当MMC1交流侧电压含有11次正序背景谐波时，其直流侧将产生10次谐波分量，此时得到的MMC1和MMC2 直流端口电压频谱分析如图14所示。

图14 MMC1交流侧含11次正序背景谐波时MMC1和MMC2直流侧电压频谱分析

由图14可知，当MMC1交流侧含11次正序背景谐波，MMC1直流侧10次电压谐波为0.909 kV，传递到MMC2直流侧时，其10次电压谐波放大至1.434 kV，此时得到谐波传递系数μ21的仿真值为1.576，与计算值1.517基本吻合。

当LCC交流侧发生单相金属接地故障时，其交流侧将产生基波负序分量，根据LCC交直流谐波传递规律，其直流侧将产生2次谐波分量，此时得到的MMC1和LCC 直流端口电压频谱分析如图15所示。

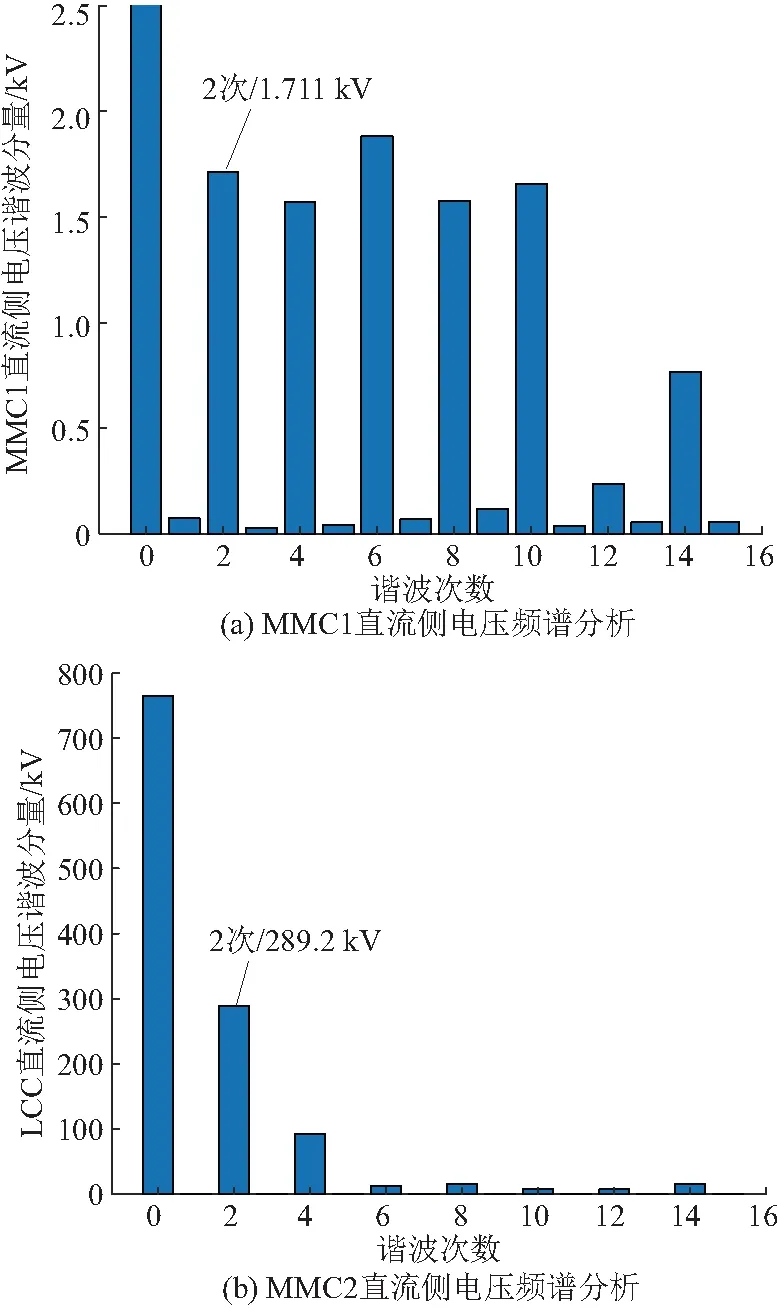
图15 LCC交流侧发生单相金属接地故障时MMC1和LCC直流侧电压频谱分析

由图15可知，当LCC交流侧发生单相金属接地故障时，LCC直流侧2次电压谐波为289.2 kV，传递到MMC1直流侧时，其2次电压谐波衰减为1.711 kV，此时得到谐波传递系数μ13的仿真值为0.005，与计算值0.006基本吻合。

基于以上分析，不同工况下谐波传递系数μ21和μ13的仿真结果与根据谐波等值阻抗得到的计算值基本相符，验证了前面基于理论等值模型的谐波传递特性分析的正确性。

4 结束语

在多端混合直流输电系统中，谐波电流通过直流线路在不同换流站之间传输，影响系统中各换流站的直流侧谐波电压。本文首先建立多端混合直流输电系统的直流侧谐波阻抗模型，通过谐波自阻抗和转移谐波阻抗、谐波传递系数的计算，得到系统的谐波传递特性，包括换流器自身及不同换流器间的传递作用。研究结果表明，多数谐波在换流站之间传递发生谐波电压传递衰减现象，少数谐波在换流站之间传递会发生谐波电压传递放大现象，可通过调节整流侧平波电抗器、直流线路长度、换流变换相电抗的值来改变系统的谐振频率和幅值。最后，通过对交流系统含背景谐波或发生故障情况下谐波在不同换流站之间的交互影响分析，证明本文所建立的系统节点阻抗矩阵中各元素能准确体现不同频段谐波在各换流站之间的谐波传递特性以及交互影响作用。