凸轮轴摆动磨削几何学建模及分析
2022-10-25陆洁李国超周宏根杨飞张娟陈浩安
陆洁, 李国超, 周宏根, 杨飞, 张娟, 陈浩安
(1.江苏科技大学机械工程学院,江苏镇江 212003;2.陕西柴油机重工有限公司,陕西兴平 713100)
0 前言
近几年来,由于船用柴油机转速与公升功率的不断提高,设计者越来越重视对配气机构的研究。柴油机凸轮型面磨削加工通常采用切入式磨削,砂轮沿直线运动,对设备及软件要求相对较低,但此方式影响砂轮的修整平整度、砂轮磨损、凸轮型面母线直线度、加工表面质量等。随着柴油机凸轮设计宽度不断增加、加工难度不断加大、加工过程中零件超差风险增大,常规磨削(CG)已不能满足当前的加工要求。
采用常规磨削加工时,即使砂轮宽度大于凸轮宽度,若工件与砂轮在加工过程中磨削接触位置始终不变,将导致砂轮局部磨损严重,砂轮加工位置出现明显凹痕,砂轮修整频繁,将使得砂轮的使用寿命大大缩短。基于金刚石和立方氮化硼(CBN)砂轮的摆动磨削(BD),当凸轮宽度大于砂轮宽度时,磨削加工过程中需要砂轮架带动砂轮沿砂轮轴向方向做往复运动,才能完成整个凸轮轮廓的磨削;不仅保证了砂轮各个地方的均匀磨损,充分利用砂轮、减小局部磨损,而且可以消除砂轮修整型面磨削精度的影响,在凸轮型面形成网状纹路,提高凸轮型面的抗磨损性能,延长零件使用寿命。
随着金刚石或CBN砂轮的重大发展,人们开始探寻材料的去除机制,基于单颗磨粒磨削的研究工作也越来越多。BUHL、汪强等人利用有限元仿真软件,推导出表面最大残余高度的计算模型,并实验验证了超声椭圆振动磨削加工过程中被加工表面质量随着振幅增加而提高,且刀具上几乎不存在积屑瘤黏附现象。邓朝晖等进行了凸轮轴数控磨削表面粗糙度实验,结果表明:在相同磨削条件下,表面粗糙度在凸轮升程处最小;凸轮轮廓不同关键部位处的表面粗糙度随砂轮线速度的增大而减小,随磨削深度的增加而变大。刘玉娇等基于超高速点磨削几何模型参数进行了研究,结果表明粗磨区倾角和偏转角的变化对接触弧长有影响。姚松林等基于超声振动辅助磨削加工表面质量进行了研究,结果表明:超声振动辅助磨削能明显提升工件表面加工质量,在一定范围内,振动频率、幅值与主轴转速的增加可以优化表面质量,进给量与切削深度的增加会削弱超声振动的优化效果。隋振等人提出凸轮磨削动态速度优化方法,相比于常用的恒角速度磨削与恒线速度磨削,该方法磨削精度较高。
虽然目前已经取得了很多的成果,但是磨削参数对摆动磨削表面质量的影响仍不明确。因此,本文作者搭建摆动磨削加工凸轮型面运动模型,并进行磨削层几何参数建模。在初设凸轮转速条件下,研究凸轮恒线速度下凸轮转动角速度和角加速度、砂轮进给速度和进给加速度的变化规律;研究接触弧长、最大未变形磨屑厚度与磨削参数的关系。
1 凸轮轴摆动磨削加工运动学建模
1.1 凸轮及砂轮运动学建模
设定轴垂直于凸轮轴轴线,轴平行于凸轮轴轴线,轴垂直于轴和轴(以下所有坐标系描述皆基于此坐标系)。摆动磨削通过凸轮轴的旋转运动、砂轮旋转运动、砂轮架沿轴往复运动、砂轮架沿轴往复直线运动,实现凸轮轴型面的加工成型。以上4种运动速度分别为、、、,如图1、图2所示。磨削过程中在凸轮表面形成致密的网状加工纹路,如图3所示。凸轮轴型面和砂轮之间必须始终保持相切。根据已知的凸轮轴旋转速度,凸轮轮廓生成数据和砂轮的旋转速度建立函数关系,从而建立凸轮轴摆动磨削运动学数学模型。
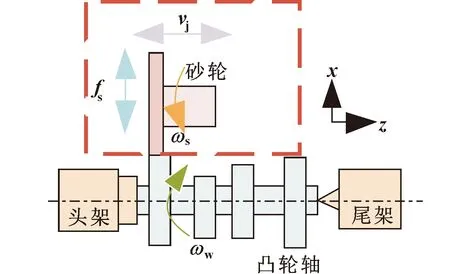
图1 摆动磨削凸轮轴运动示意
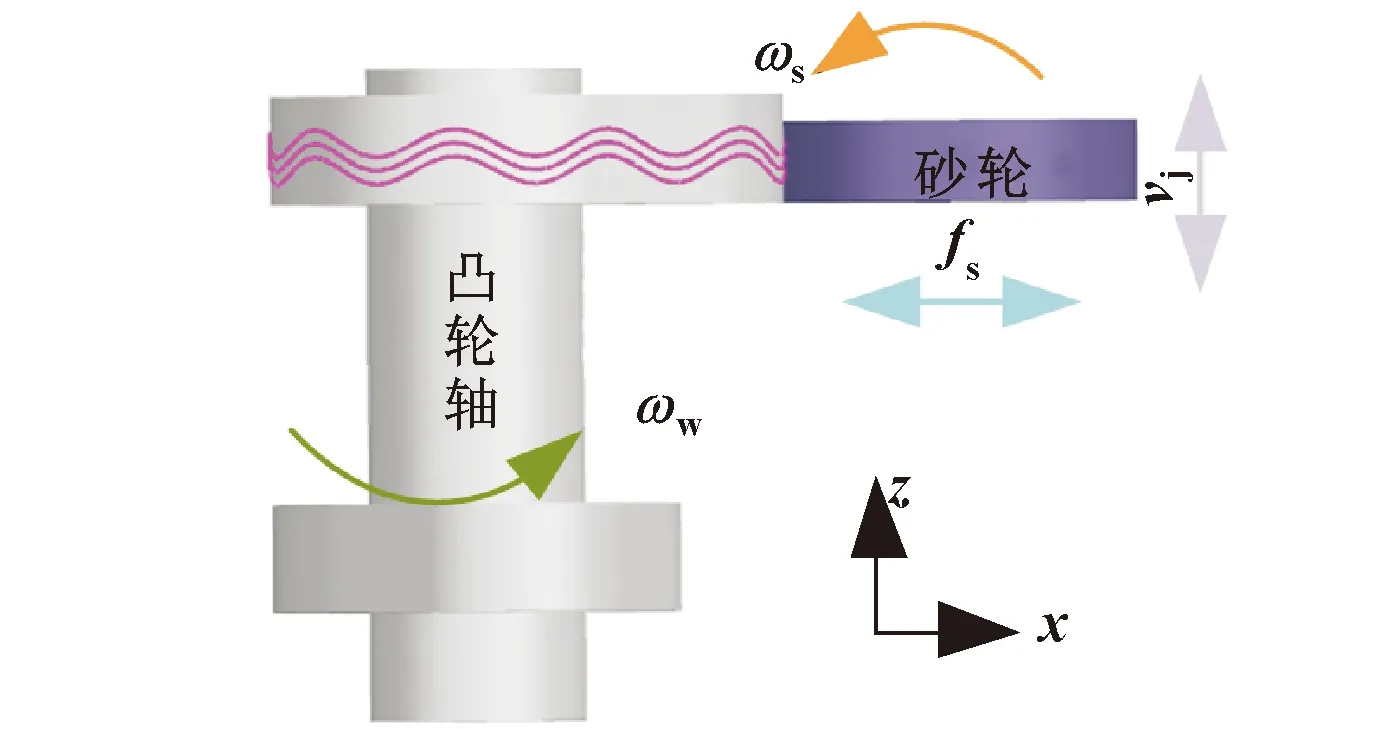
图2 摆动磨削凸轮轴三维示意

图3 摆动磨削已加工表面
摆动磨削凸轮与砂轮约束关系如图4所示。为计算方便引入滚子从动件,凸轮、砂轮、滚子从动件始终保持相切。
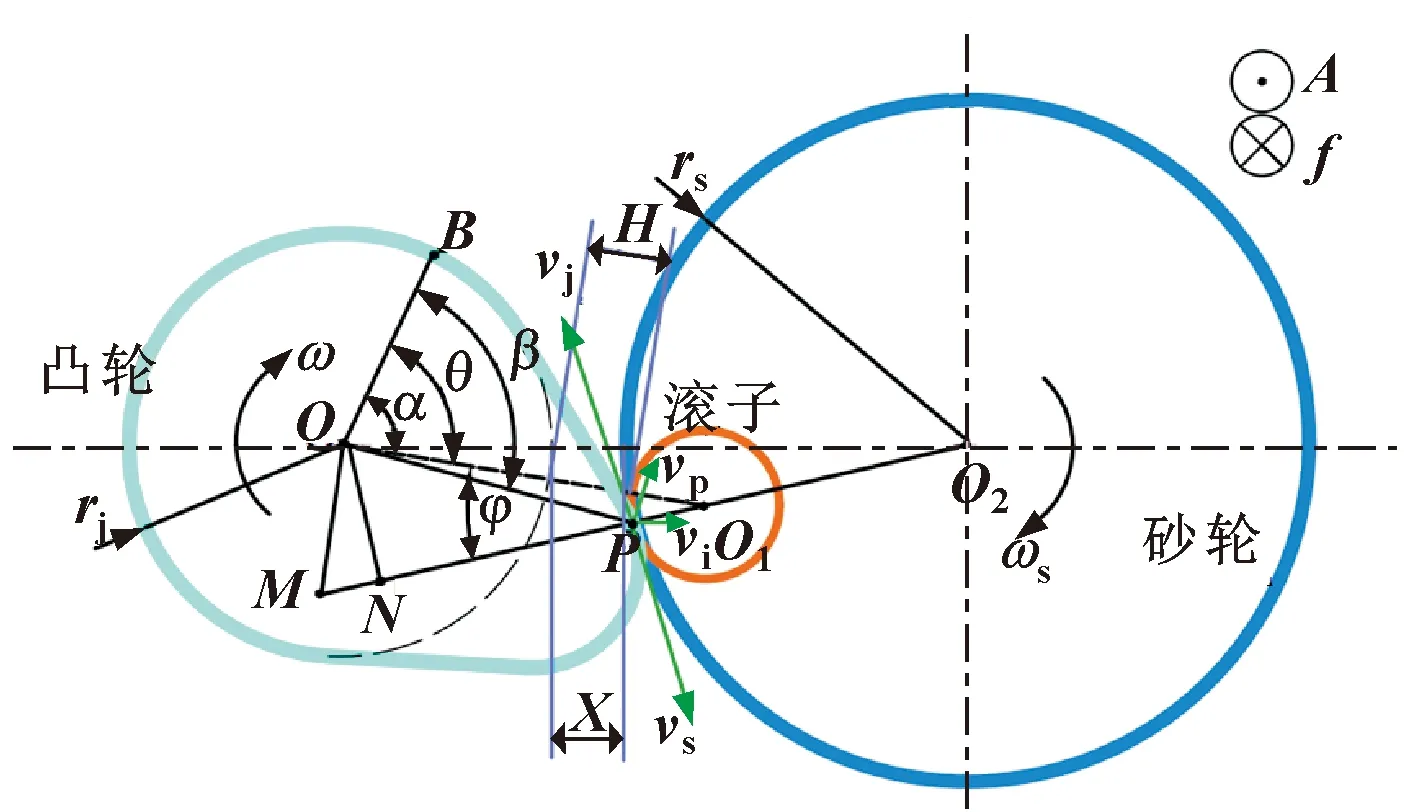
图4 凸轮-砂轮约束关系示意
凸轮升程表中的升程关系记作(),点为凸轮和滚子从动件的速度瞬心,记作⊥。如图5所示,′为滚子从动件相对凸轮表面的滑动速度,为凸轮点旋转线速度,d/d为滚子从动件移动速度。考虑⊥,′⊥,(d/d)∥,可得△与由、′、d/d组成的速度三角相似,即:
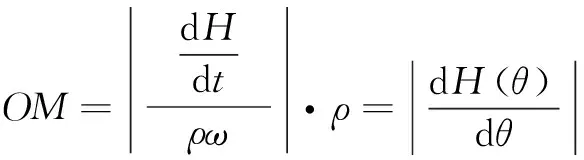
(1)
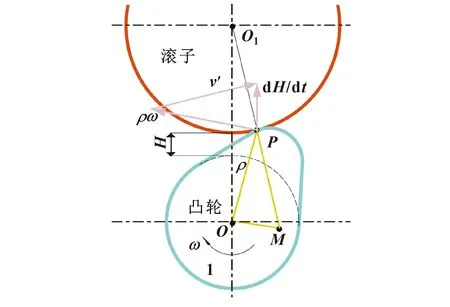
图5 凸轮-滚子约束关系示意
为凸轮的旋转中心到滚子从动件的直线距离:
=++
(2)
其中:为凸轮基圆半径;为滚子从动件半径。
辅助计算角为与的夹角:
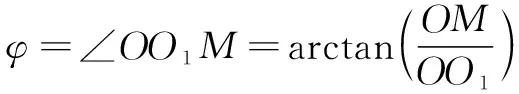
(3)
图4中⊥,由三角关系得砂轮与凸轮旋转中心之间的距离:

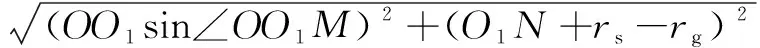
(4)
其中:为砂轮半径。
由图4可知,砂轮架沿轴的往复进给距离:
=()=--
(5)
实际加工零件时,需要获得凸轮转角每转1°对应的,则需要先求出与的关系:
=()=-∠=-(∠-
∠)
(6)
将方程(5)(6)进行拟合,即可获得凸轮每旋转1°,砂轮中心沿轴的运动位移。
凸轮型面由不同曲率的圆相切形成,常规外圆磨削采用恒角速度磨削,使得各个磨削点线速度、磨削力不等,导致凸桃部分磨削过量、表面产生波纹、烧伤等。因此提出凸轮轴作恒线速度运动,可消除常规外圆磨削的缺点。
凸轮基圆中心至磨削点距离为极径:

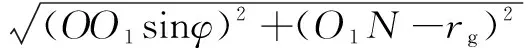
(7)
从磨削开始到某一时刻时的磨削转角为
=+∠=+(∠-∠)(8)
设凸轮恒线速度旋转时的角速度为,则磨削点在坐标系中的运动速度为
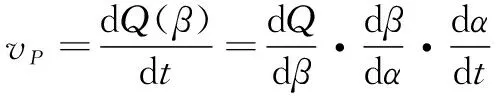
(9)
基圆段的角速度为,要使得凸轮表面各个磨削点的线速度与基圆段相同,只需要令:
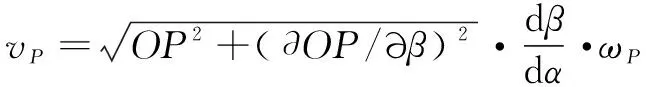
(10)
凸轮轴恒线速度转动时的角加速度公式为
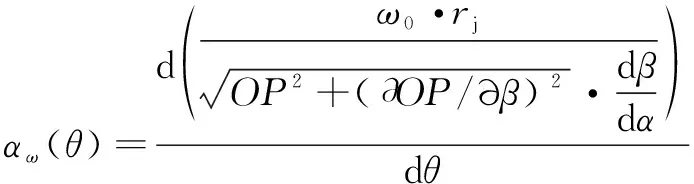
(11)
砂轮沿轴的运动速度关系式:
=sin∠-sin∠
(12)
其中:为凸轮旋转产生的分解为水平方向的移动速度;为凸轮的切点速度;为凸轮在磨削运动中的速度。砂轮沿轴的运动加速度为
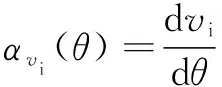
(13)
1.2 砂轮磨粒瞬时运动学建模
常规磨削单磨粒磨削轨迹和摆动辅助磨削单磨粒磨削轨迹如图6所示,摆动磨削砂轮的运动轨迹为正弦函数。单个磨粒的磨削过程可近似于刀具的切削过程,为了简化分析模型,分析单颗磨粒的磨削过程。
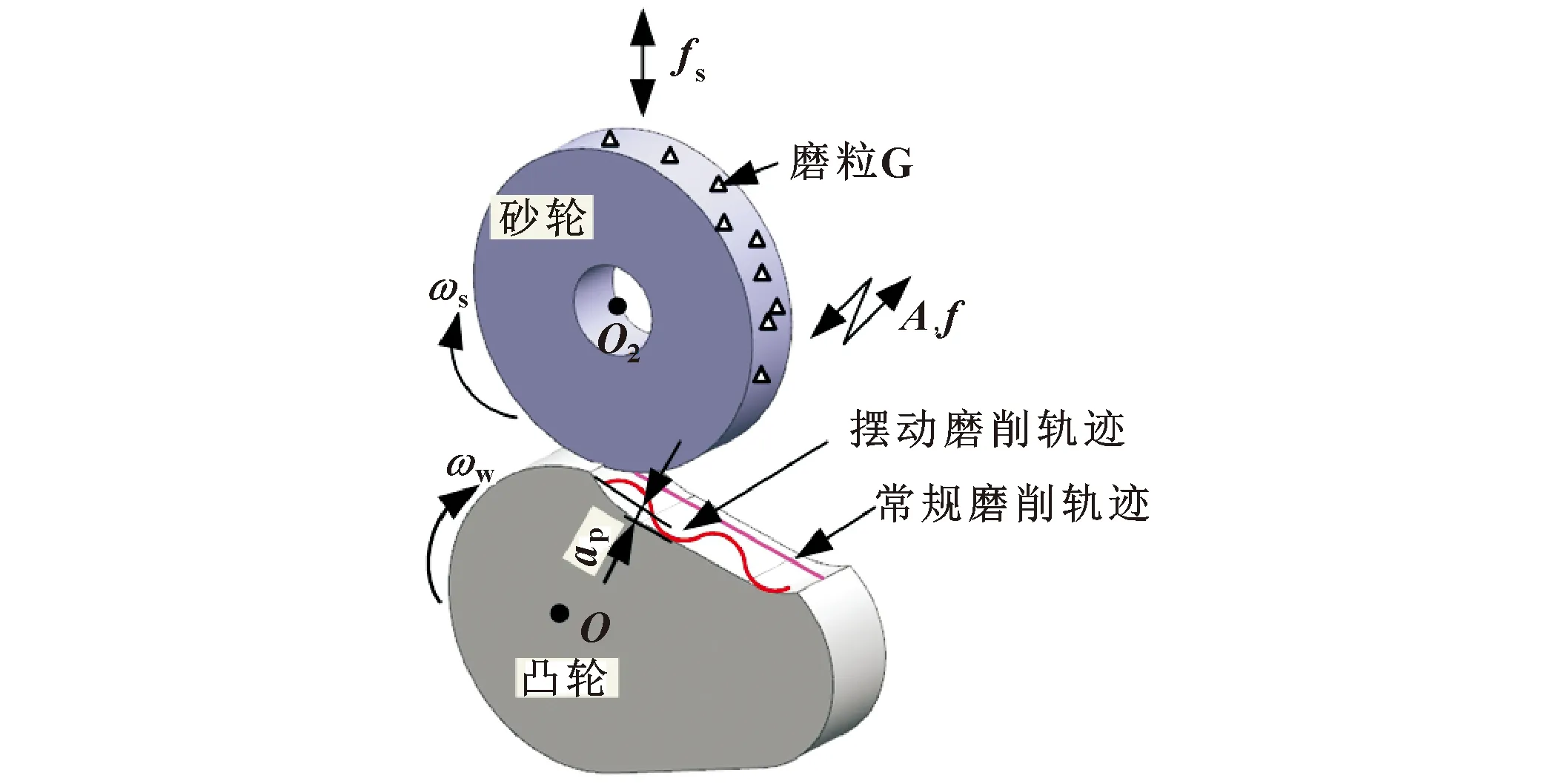
图6 单磨粒在单位接触时间内凸轮表面磨削轨迹
由于磨粒的磨削运动复杂,很难对磨削过程进行完整的描述设计。因此,主要提出以下假设和简化:
(1)所有磨粒都是刚性的;
(2)不考虑磨粒之间的弹性、热变形,且磨粒的分布均匀;
(3)砂轮表面上所有磨粒都具有同一高度,并且全部参与磨削。
砂轮单个磨粒经过接触-分离区间需要用时Δ,如图6所示,磨粒G在坐标系中的运动过程可以分解为绕砂轮中心做旋转运动,转速为;沿轴做往复运动,振幅为;沿轴做进给运动,速度为。磨粒G接触-分离时间Δ为
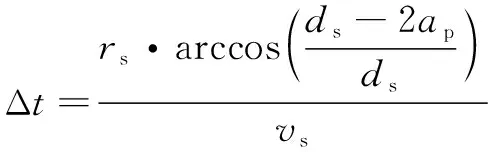
(14)
其中:为砂轮磨削深度,计算公式为

(15)
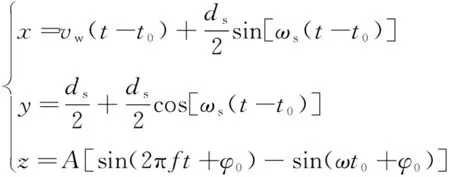
(16)
令=0、初始相位角=0,将式(16)化简为摆动磨削时单颗磨粒的磨削运动方程:

(17)
对上式求导,可得轴向摆动辅助磨削过程中单颗磨粒G的运动速度方程:
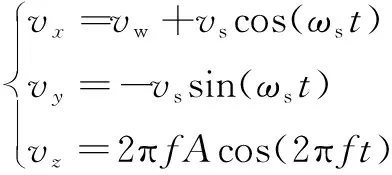
(18)
2 摆动磨削磨削层几何参数建模
2.1 摆动磨削单磨粒接触弧长
由于单磨粒的摆动幅度大、摆动频率小,摆动磨削单磨粒接触弧长在磨削时间内呈现出正弦函数的一小部分。凸轮在时刻,磨削点为,时刻磨削点为,如图7所示,且-为单磨粒在砂轮的一个旋转周期内与凸轮的接触时间Δ。

图7 摆动磨削接触弧长
因此摆动磨削中单磨粒切削弧长为
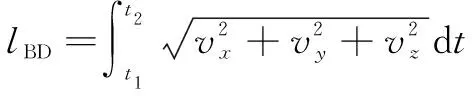
(19)
由文献[1]可知,常规磨削的接触弧长为

(20)
2.2 摆动磨削最大未变形磨屑厚度
磨削时的最大未变形磨屑形状为图8中所示的曲边四边形,用表示。最大未变形磨屑厚度影响作用在磨粒上力的大小、磨削比能、磨削区温度,从而对砂轮的磨损以及表面粗糙度产生影响。
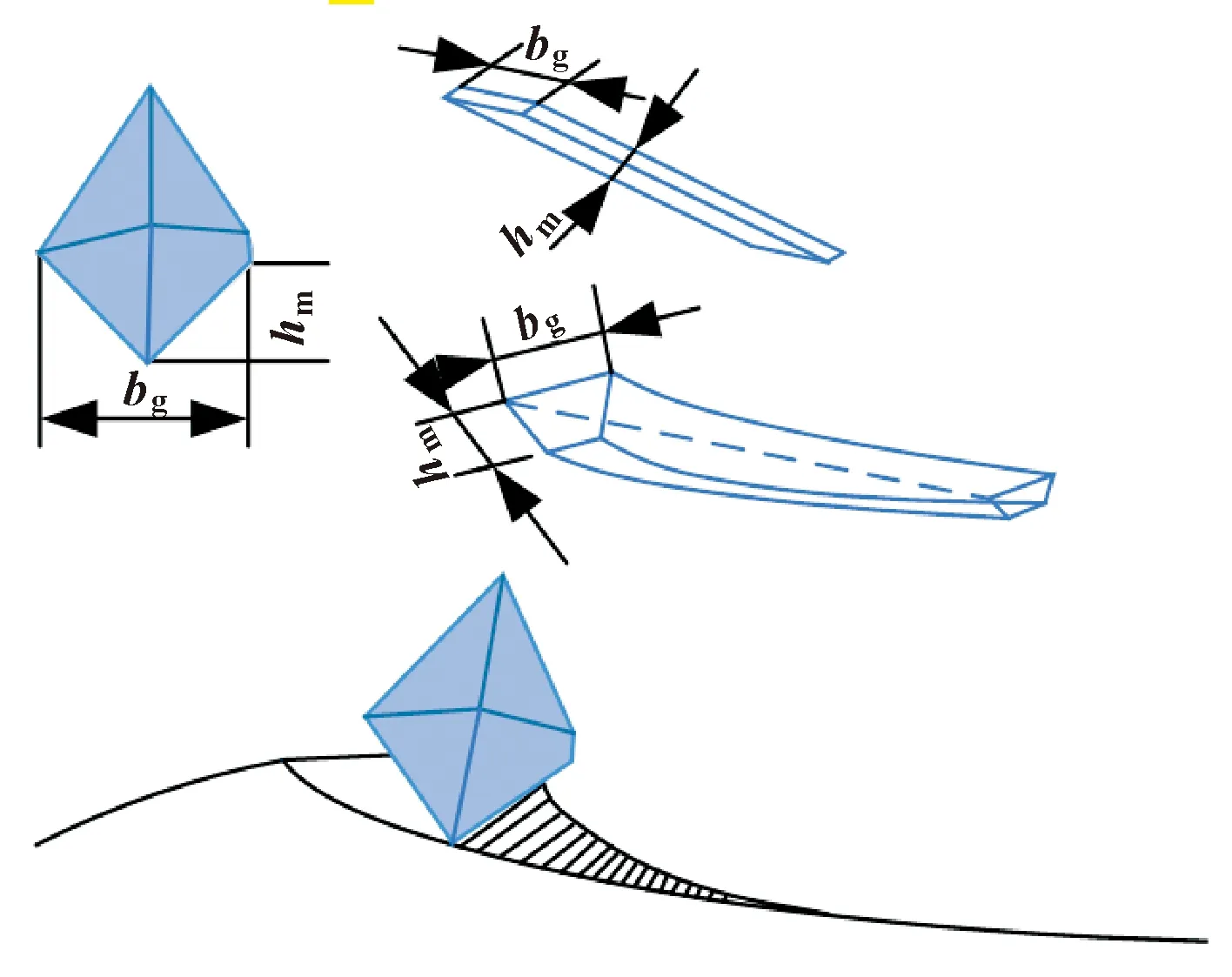
图8 未变形切削厚度hm示意
根据磨屑体积不变的原则,采取未变形磨削的断面积导出磨削厚度公式:
==
(21)
=2π=
(22)
其中:为单位时间内下所有活性磨粒形成的磨屑总体积;为最大磨削截面积;为砂轮宽度;为几何接触弧长;为砂轮单位时间内去除材料量;为砂轮表面圆周上的磨粒数;为磨削刃密度。
摆动磨削动态接触弧长中几何接触弧长和动态弧长之间存在一定的比例关系:
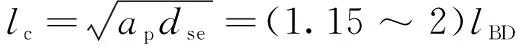
(23)
磨削最大磨削截面积:
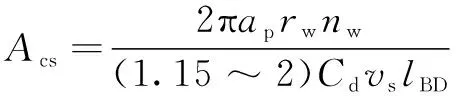
(24)
最大未变形磨屑厚度为
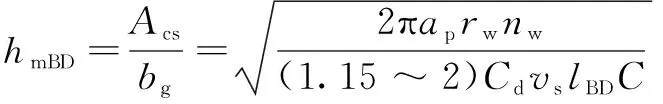
(25)
其中:为比例系数,与磨粒顶角有关;为磨削宽度,=·。
常规磨削最大未变形磨削厚度:
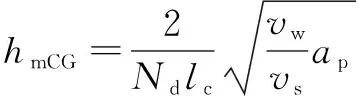
(26)
3 摆动磨削运动学分析及磨削层几何参数分析
3.1 磨削运动学分析
使用的凸轮轮廓生成数据如表1所示。采用三次样条插值对凸轮轮廓节点进行插值后,利用MATLAB软件绘制凸轮轮廓。图9所示为插值后的升程曲线,图10所示为凸轮轮廓曲线。
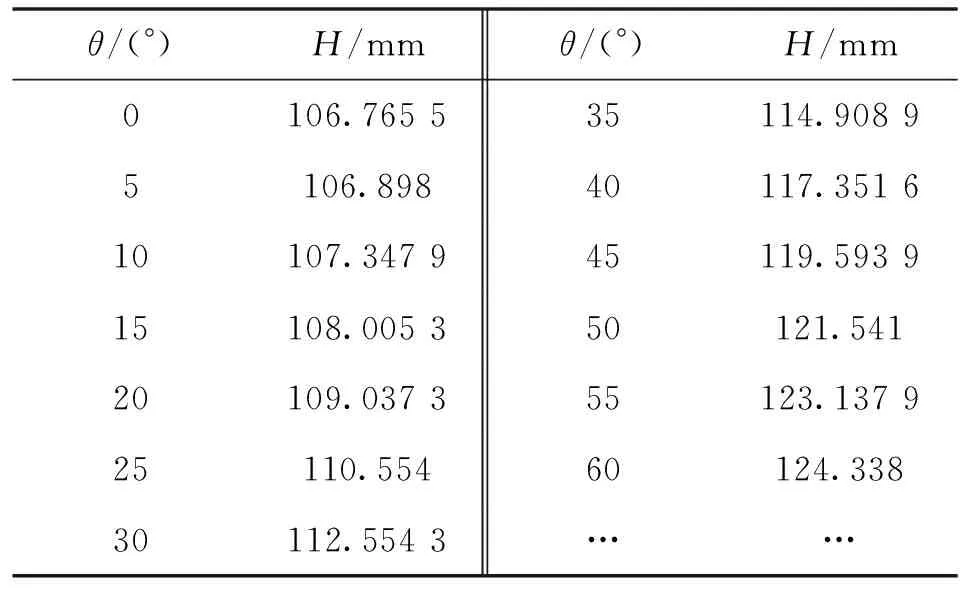
表1 凸轮部分轮廓生成数据
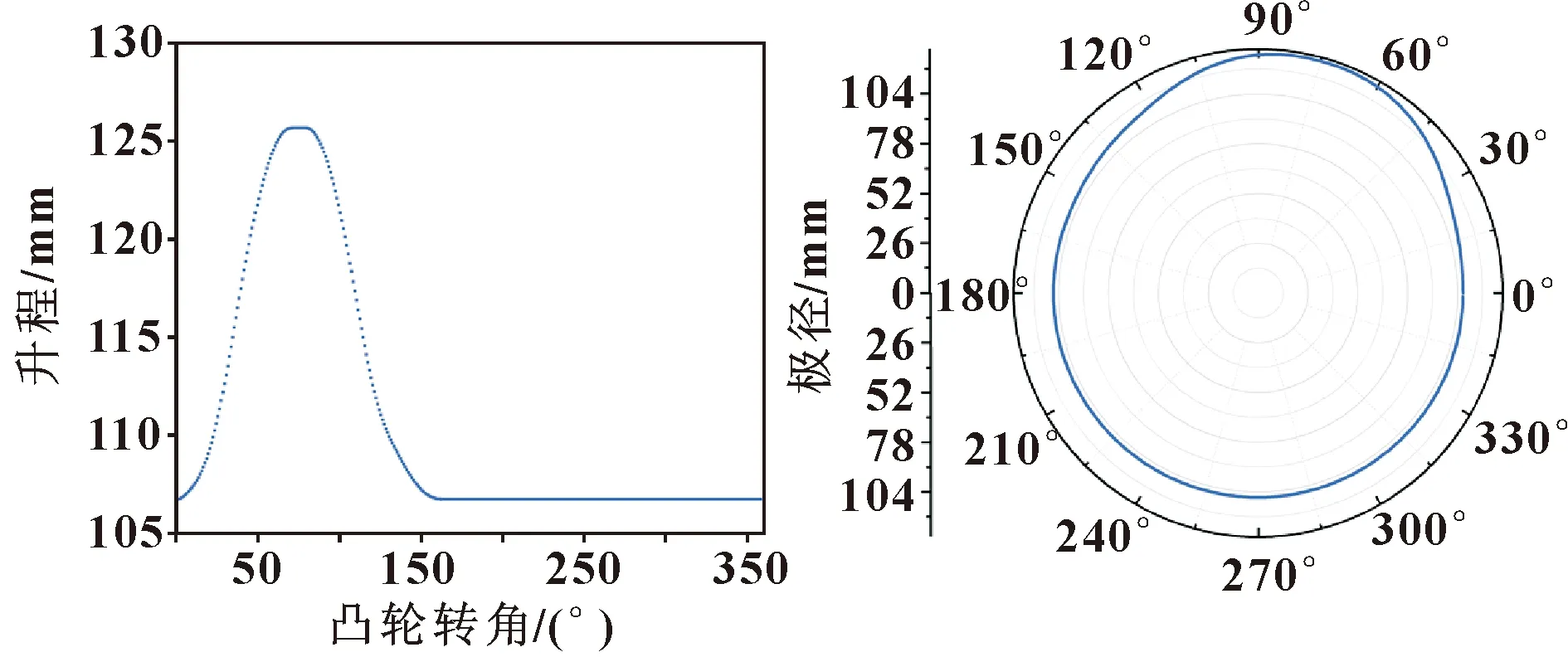
图9 插值后的升程曲线 图10 凸轮轮廓曲线
根据公式(5)得到凸轮转角和砂轮进给位移曲线,如图11所示。凸轮轴采用恒线速度运动,根据公式(10)(11)得到凸轮转角和凸轮转速曲线和角加速度曲线,如图12所示。根据公式(12)(13)得到凸轮转角与砂轮进给速度曲线和加速度曲线,如图13所示。
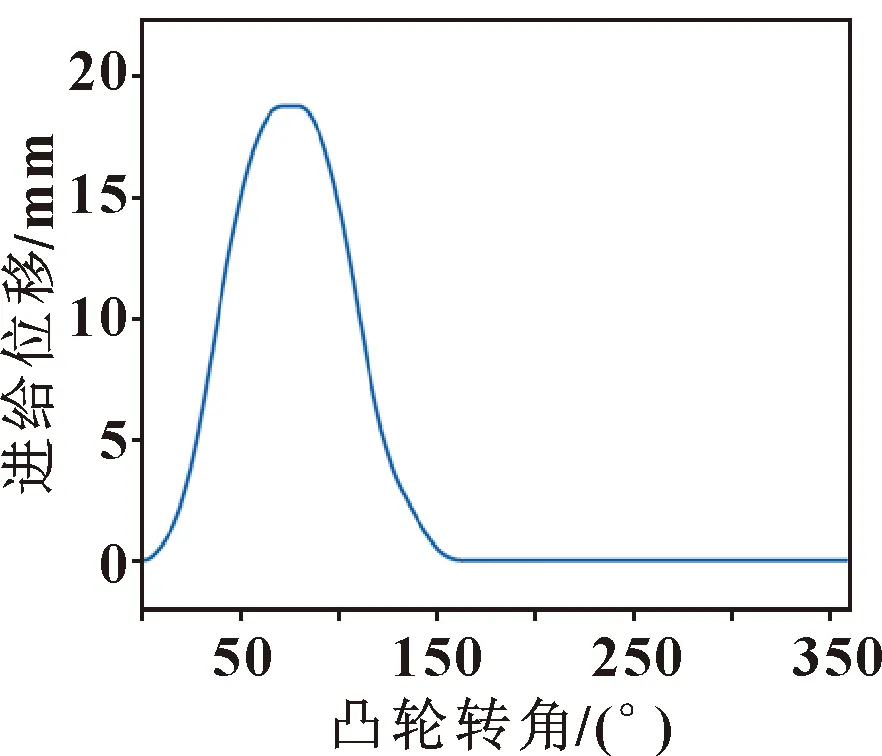
图11 砂轮架进给位移
由图12、图13可以看出:随着凸轮轴的速度增加,凸轮轴的转动角速度、转动角加速度和砂轮进给速度、砂轮进给加速度都呈现线性增长趋势。当凸轮轴旋转时,砂轮进给速度是关于转角的正弦函数,所以砂轮进给既没有速度突变,也没有加速度突变,满足工程实际要求。
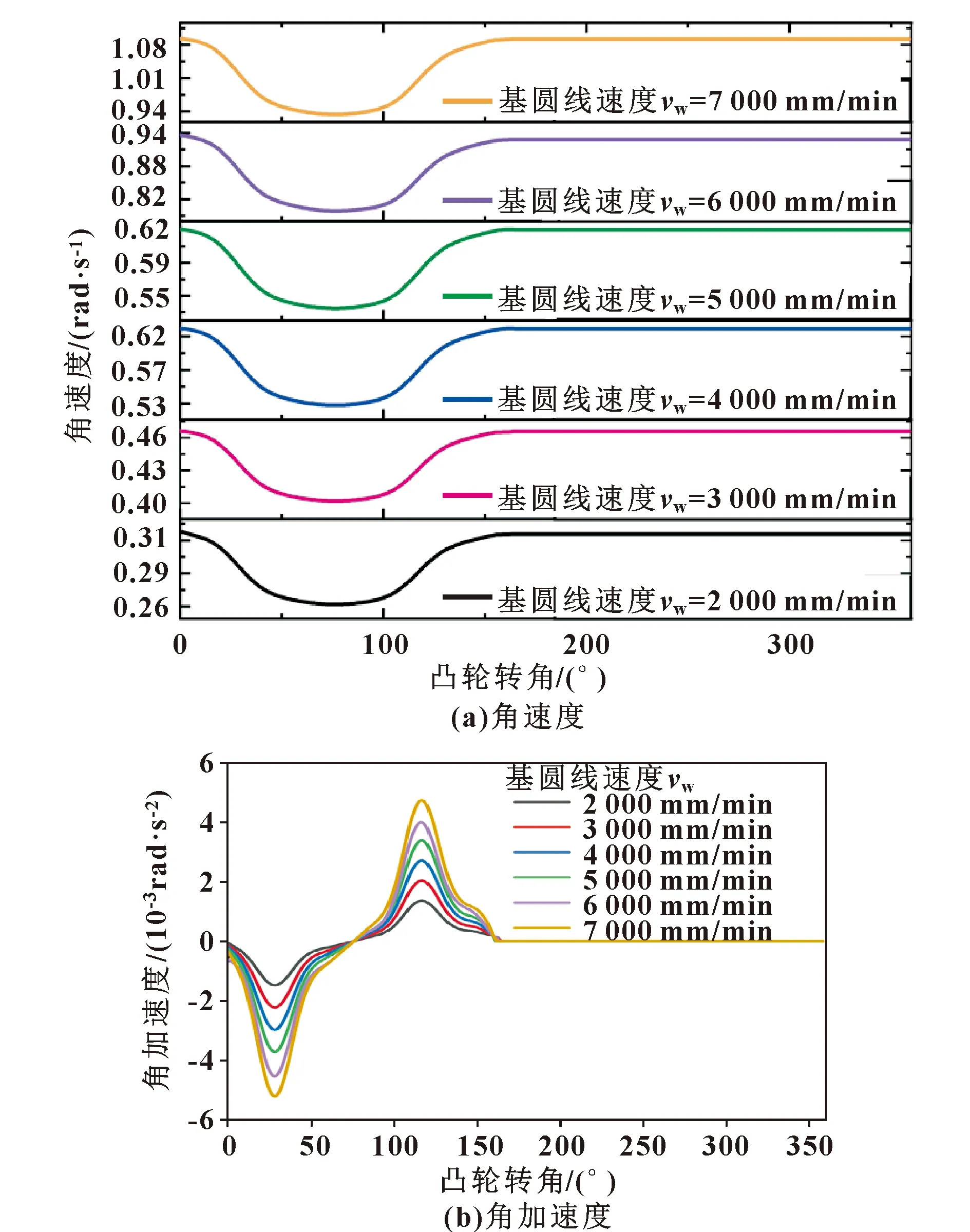
图12 凸轮转角与凸轮磨削点角速度和角加速度关系

图13 凸轮转角与砂轮进给速度和进给加速度关系
3.2 摆动磨削磨削层几何参数分析
为探究摆动磨削时磨削参数对加工表面形貌的影响规律,基于MATLAB软件进行控制单一变量仿真,仿真参数如表3所示。
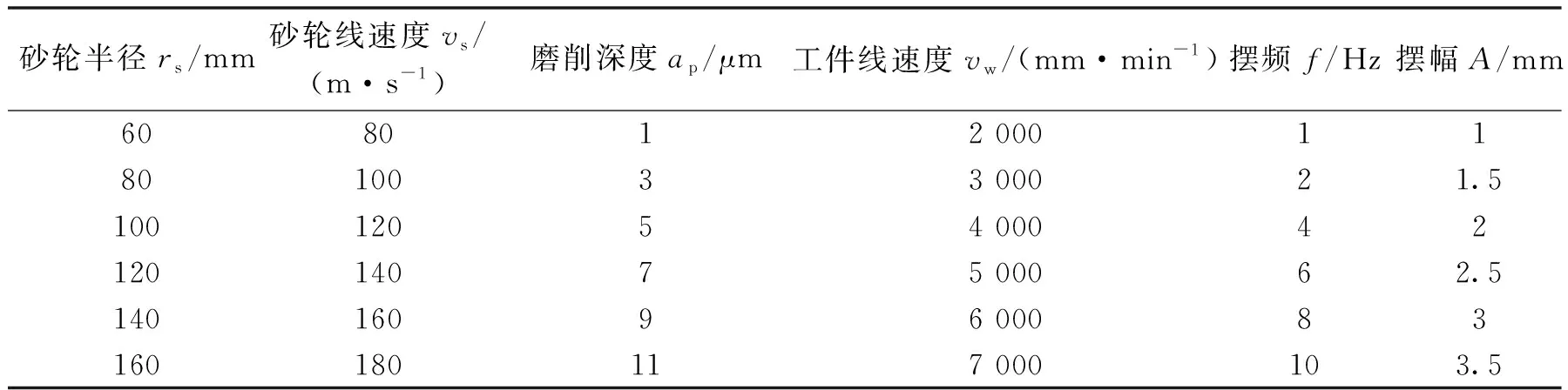
表3 单因素控制变量仿真参数
磨削接触弧长越长,凸轮表面越光滑,表面质量越好。图14所示为不同磨削参数对磨削接触弧长的影响。可知:摆动磨削和常规磨削在同一磨削参数不同取值时变化趋势一致,但是比长;图(a)表明和成正比,越大不仅越不利于加工有凹面的凸轮轴,而且还会使砂轮产生振动,影响凸轮型面的加工;图(b)表明和呈现反比,其中综合选取=400 mm,=120 m/s,=2 000 mm/min,=0.003 μm,=1 Hz,=1 mm时,最大;图(c)表明对影响很小,较高的主轴转速对于抑制裂纹产生、降低粗糙度都有积极作用,但是过高的转速会降低系统的稳定性;图(d)表明对的影响最大。图(e)和(f)的初始值为916.891 8 μm,表明和对影响很小,可忽略,加入频率和振幅可以提高接触弧长,提高表面质量。但是过大的或者会加重表面纹理的形成,影响表面质量。
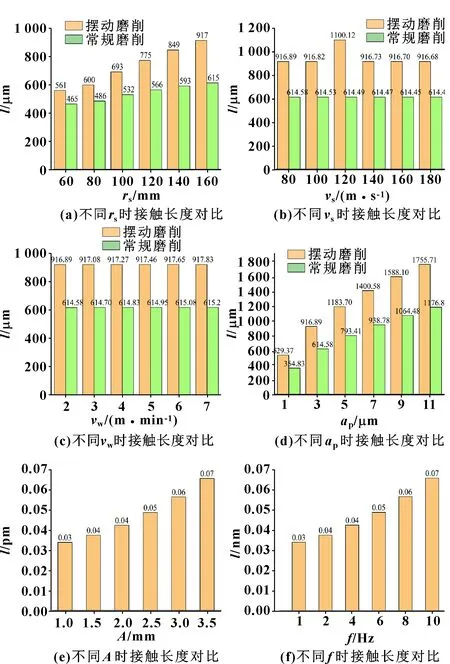
图14 不同磨削参数下摆动磨削和常规磨削的接触弧长对比
通过MATLAB对最大未变形磨屑厚度进行仿真,最大未变形磨屑厚度越小,凸轮型面表面越光滑,表面质量越好。不同磨削参数下摆动磨削和常规磨削的最大未变形磨削厚度对比如图15所示。可知:最大未变形磨屑厚度和接触弧长有着类似的规律,和的变化趋势一致,但是比h小,越小,磨削表面越光滑;图(a)表明和成反比,越大则越不利于加工有凹面的凸轮轴;图(b)表明与先成反比再成正比,但是变化幅度较小;图(c)表明和成正比。6个因素中,对的影响最大。图15(e)(f)的初始值为0.255 397 7 μm,和对的影响较小,可忽略,但对比发现加入和可降低最大未变形磨削厚度。
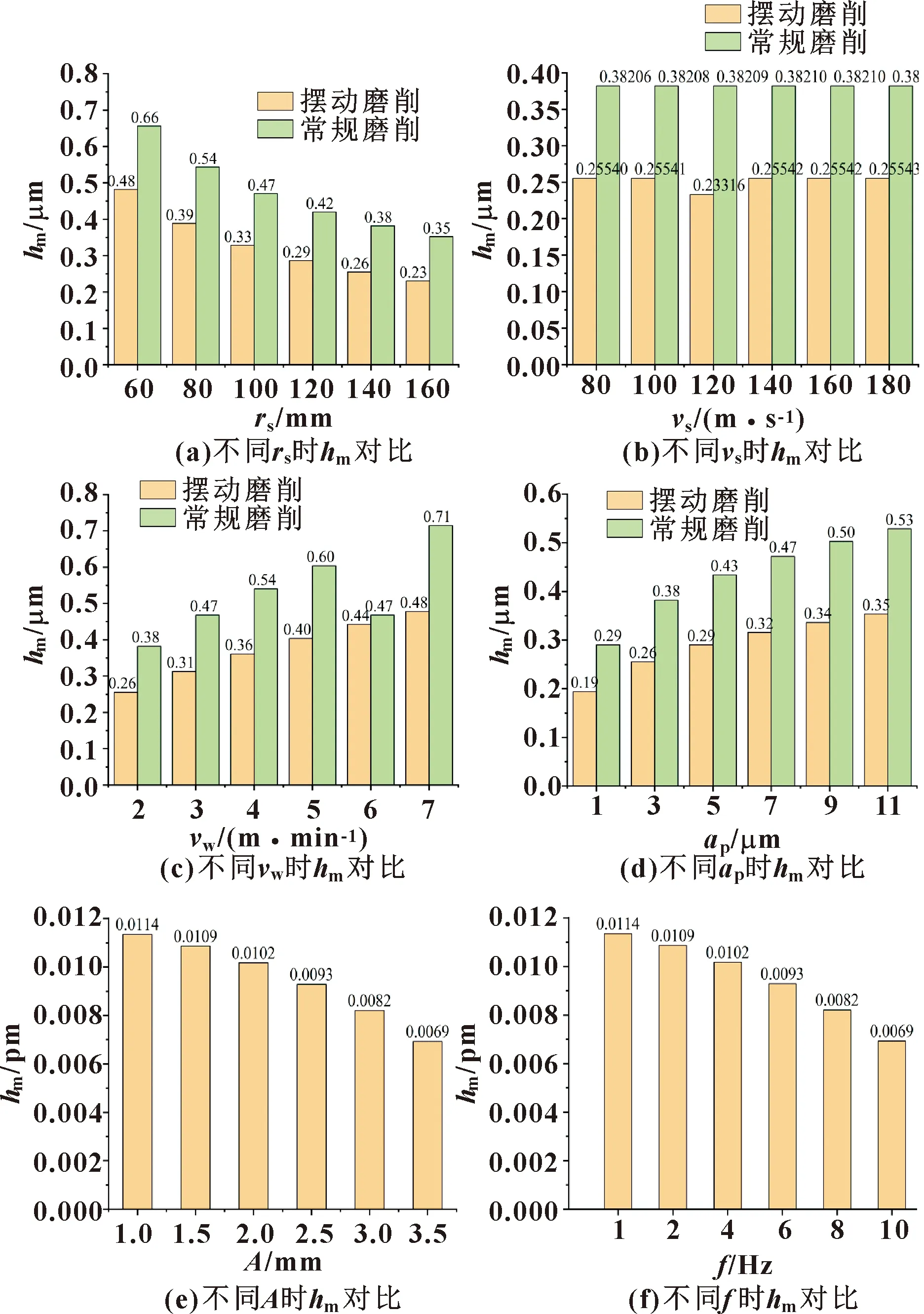
图15 不同磨削参数下摆动磨削和常规磨削时的最大未变形磨削厚度对比
不仅需要考虑磨削参数对和的影响,而且还需要考虑磨削参数变化时,对凸轮旋转一周时各个磨削点的影响。将凸轮型面分为360°进行分析,结果如图16—19所示。
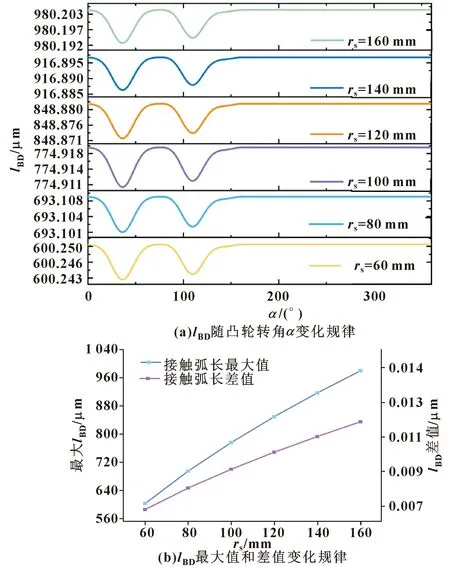
图16 不同砂轮半径时摆动磨削接触弧长变化规律
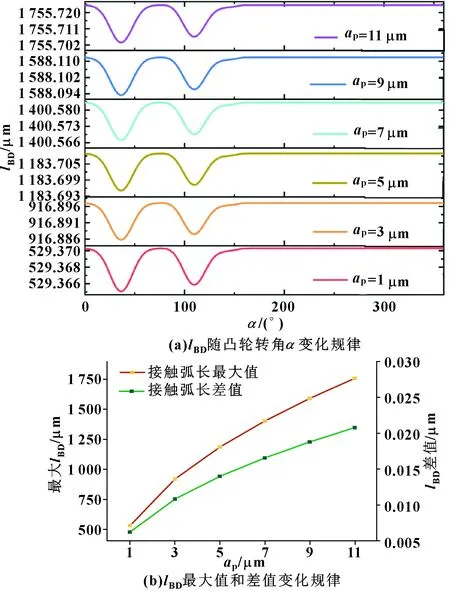
图17 不同磨削深度时摆动磨削接触弧长变化规律
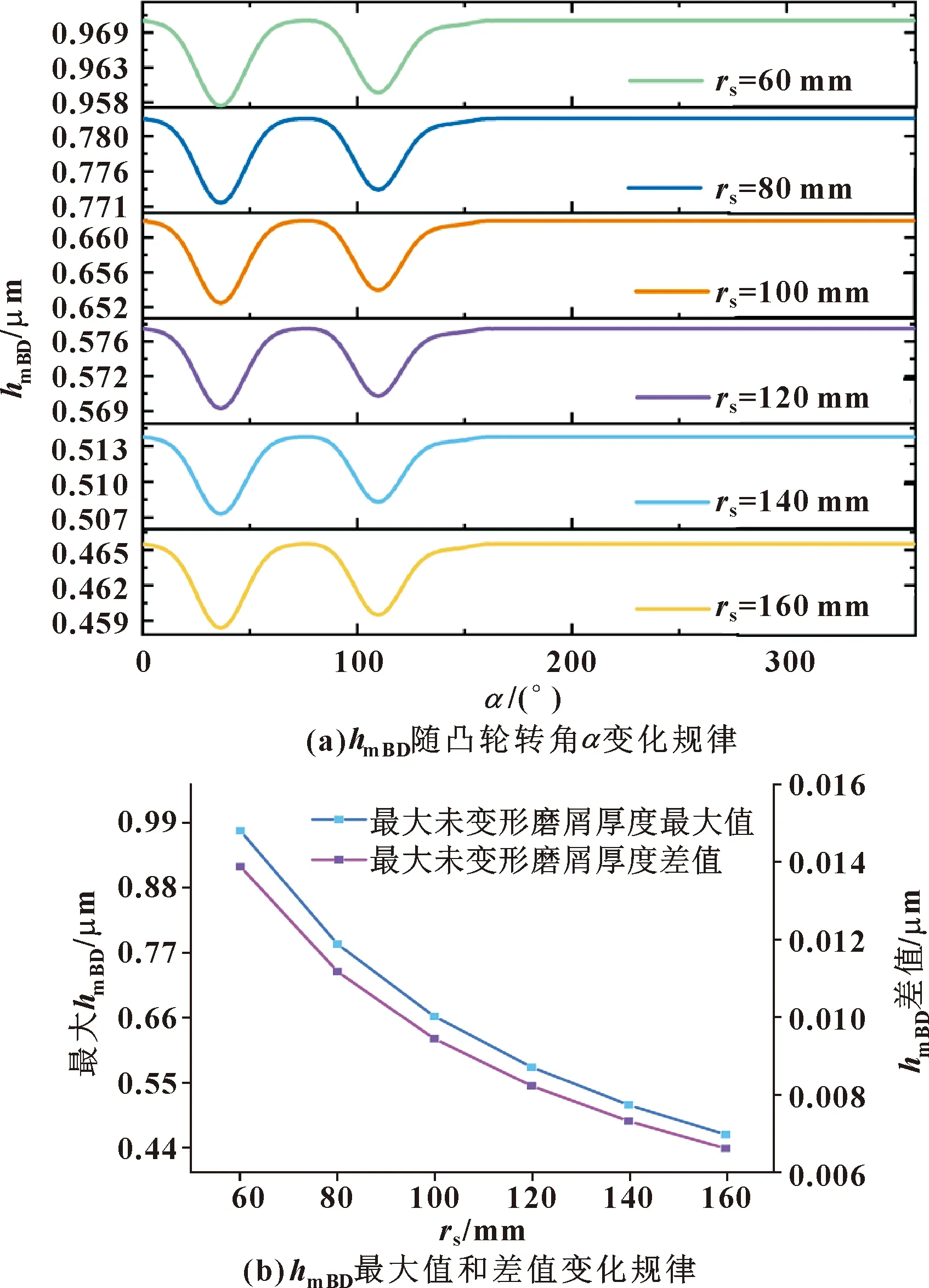
图18 不同砂轮半径时摆动磨削最大未变形磨屑厚度变化规律
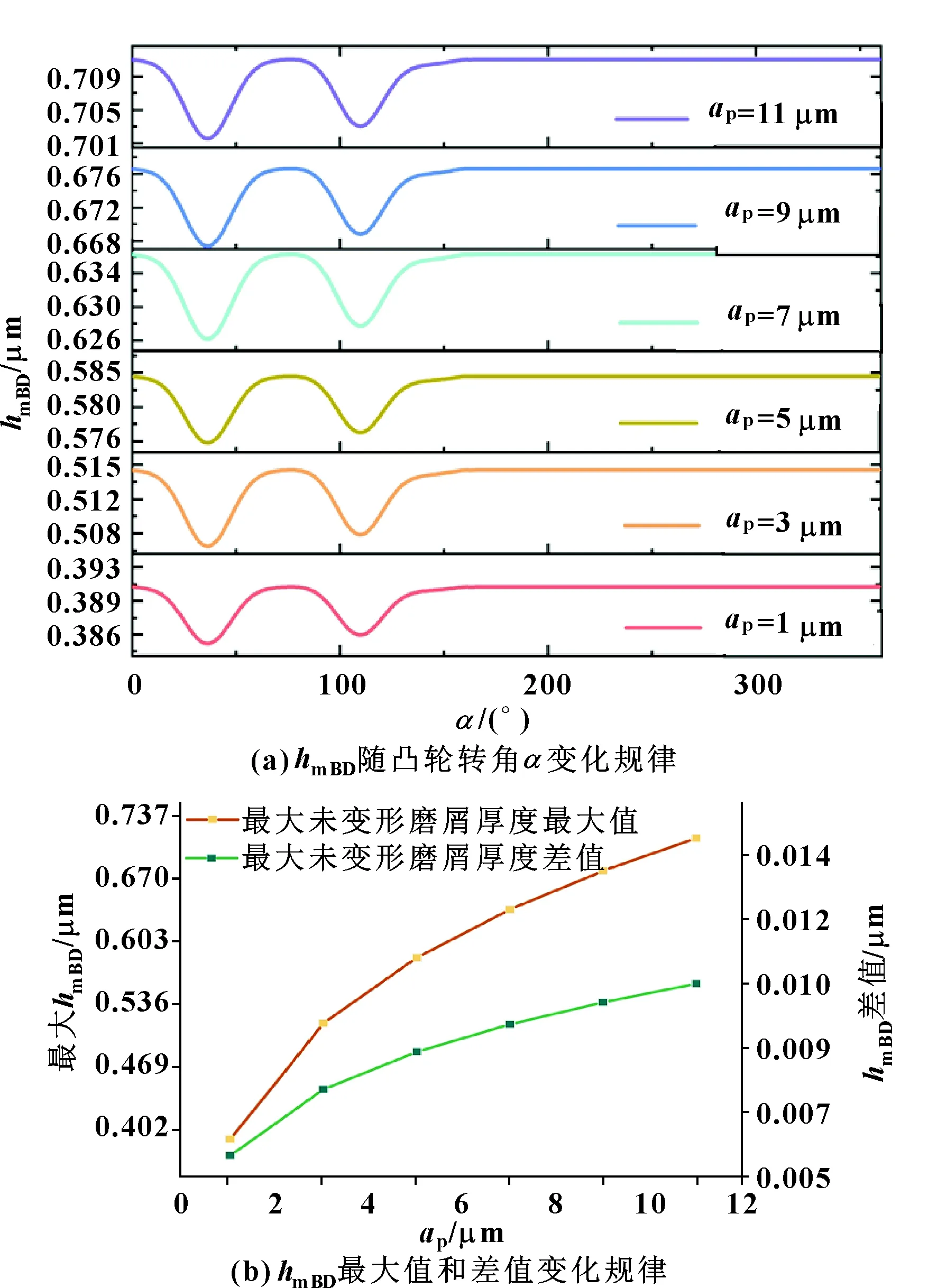
图19 不同磨削深度时摆动磨削最大未变形磨屑厚度变化规律
选取对磨削接触弧长和最大未变形磨屑厚度影响最显著的2个磨削参数和进行分析。由图16—图19的图(a)可以看出:和在凸轮的升程回程部位均匀过渡,过渡段磨削表面质量好,在基圆部分无变化。由图16—图19的图(b)可以看出:和h的最大值、最大值和最小值的差值呈线性关系。
4 结论
通过运动学建模和磨削层几何参数建模,对摆动磨削表面形成机制进行理论分析。结果表明:磨削深度对表面质量影响最大,磨削深度越大,接触弧长越长,磨削表面质量好,但此时最大未变形磨屑厚度越大,磨削表面质量差,并且近似呈线性关系;适当增大砂轮直径、砂轮转速、凸轮速度、摆动幅度、摆动频率,能提高磨削表面质量。
