雷击金属管管内线缆耦合特性分析

李祥超，文巧莉，李诗怡，欧阳文，储 蕾

(南京信息工程大学气象灾害预报预警与评估协同创新中心，南京 210044)

0 引言

伴随着高度集成与快速通信网络的各种系统的快速发展，电缆已经成为电力与通信系统的主要组成部分，并且占据了重要的地位。自然界中雷电可能形成的较强的雷电电磁脉冲并通过电缆耦合造成过电压，使得终端设备受到电磁干扰甚至损坏等问题引起了人们的重视[1-4]。因此，结合实际情况研究线缆对雷电电磁脉冲的耦合特性，从而减小耦合过电压带来的损失，这是一个十分重要的课题。

国内外很多学者针对线缆对雷电电磁脉冲耦合、架空线路雷电感应过电压等做了相关研究[5-8]。有3种主要的国际公认模型来描述外电磁场对导线的耦合，分别是Taylor[9]模型，Agrawal[10]模型和Rachidi[11]模型。罗小军等人采用FDTD建模，仿真分析了当雷击高塔时，附近的埋地线缆的耦合特性，并且与雷直击大地附近埋地线缆的耦合特性作对比，发现雷击高塔比雷直击大地时附近的埋地线缆的耦合感应电压波形的时间拉长且出现衰减振荡的现象，耦合感应电压幅值更高[12]。杨春山等人采用传输线模型研究雷电电磁脉冲对地面附近电缆的耦合效应，发现了即使距离雷击点仅几十米的近地线缆，在线缆的外部都有可能耦合感应到几万伏到几十万伏的电压，即使是采用屏蔽效能很好的线缆，在终端上也可能感应产生几伏到几十伏的感应电压，这对耐压只有几伏的微电子设备将造成严重的损伤[13]。李祥超等人通过冲击试验对架空电缆对雷电电磁脉冲的耦合特性进行了分析，发现了耦合电压与架空电缆的高度有关[14]。这些对研究都对线缆耦合过电压及其雷电防护具有重要的指导意义。

但是针对雷电直击金属管对管内线缆耦合特性进行分析几乎没有。在日常生活中，在室外不乏看见高耸的金属管内穿有线缆(通讯铁塔、路灯、室外监控器等)，也经常有雷电击中金属管的情况，结合实际应用，笔者采用理论与试验结合的方法，对金属管进行雷电流注入冲击试验，分析金属管内线缆终端在不同接线情况下耦合到的电压波形、频谱特性、以及耦合电压峰值、能量与管径关系。并通过曲线拟合，反推出实际情况下雷击金属管，管内线缆终端可能耦合到的电压峰值。这对后端雷电防护设计具有一定的实际参考价值。

1 理论分析

1.1 金属管与同轴线间的电场

将同轴线与金属管看成两个无限长的导体空心圆柱筒C1、C2，见图1，半径分别为R1、R2(R2>R1)，两空心圆柱筒轴线间的距离为d(轴线一致则d=0)，因为在垂直于空心圆柱筒的所有横截面的电场分布情况相同，因而可看成是一个二维电场，可只取其中任意一个平面进行讨论。

因为两个空心圆柱筒电荷分布是关于x平面对称的，像电荷一定在x轴上。设C1、C2分别带单位长度的电荷量为λ、λ′，C1、C2对应的相电荷分别在A、B两点。由于柱面为等势面，所以柱面上任一点电场强度的切向分量为零，则有

令

|O1A|=l1，|O1B|=l2，|O2A|=d1，|O2B|=d2,

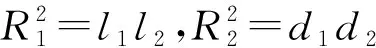
(1)

由图1可知

d1=l1+d，d2=l2+d

(2)

由公式(1)、(2)得：

在两空心圆柱筒间任一点P(x,y)的电势可表示为[15]

(3)

若C2接地，则u|r=R2=0，设P点位于空心圆柱筒C2与x轴交点上，则PB=d2-R2，PA=R2-d1(或PA=R2+l1)，这时

(4)

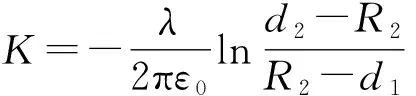
两空心圆柱筒间任一点P(x,y)的电势为

(5)

1.2 同轴耦合理论

当同轴线缆耦合了雷电电磁场后，在其外表皮上会产生一定的电流，见图2。因同轴线金属屏蔽层的屏蔽能力有限，外表皮产生的电流将透过屏蔽层，并且在芯线中产生电压，由于存在阻抗，这一电压又会形成电流[16]。

图2 同轴电缆的几何图形

图中E为电场，I(z)为屏蔽层电流分布，b/2为线缆距地面高度，d为线缆的外直径。Z1/2，Z2/2为将线缆屏蔽层当作地面上的传输线的阻抗，Za、Zb为内部负载阻抗，Z0/2为将线缆屏蔽层当作地面上的单线传输时的特性阻抗，Zc为线缆内部的特性阻抗，IL为内部负载阻抗Zb中的电流。

线缆终端的电流可表示为

(6)

式中：

s为线缆长度，单位m；

ω=2πf；

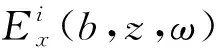
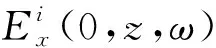
由于K(z,ω)=ZTI(z,ω),ZT为线缆的转移阻抗，且Ex=0，所以内部负载阻抗Zb中的电流IL(ω)为

(7)

式中：

ω=2πf；

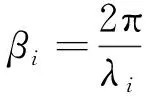
则线缆芯线上终端电压可表示为

V(s,w)=IL(w)Zb

(8)

线缆屏蔽层上电流分布可由两端以电压发生器激励的双传输线的解来推导，沿z方向行进的场强为

(9)

若取z=0处作为相位参考点，则线缆左右侧终端的场强分别为

(10)

(11)

而线路终端的电压发生器为

(12)

(13)

根据电压发生器在两端激励的传输线的解，可以得到下式线缆屏蔽层上的电流分布：

j(Z0+Z2)sinβs·cosβz-

j(Z1+Z2)cosβs·sinβz}

(14)

则屏蔽层终端电压可表示为

(15)

2 试验方案及试验数据的分析

2.1 试验方案

为了测试金属管内的线缆对雷电电磁波的耦合特性，利用8/20 μs冲击平台模拟雷电流并注入金属管，冲击电流从5 kA到35 kA，步长为5 kA。并利用示波器采集管内金属线缆终端在不同接线情况下的耦合数据。其试验模型见图3。

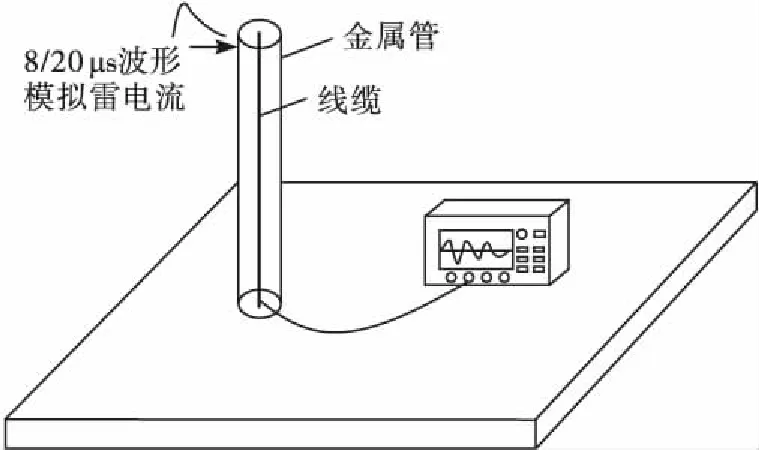
图3 实验模型

根据实际应用的情况，选取3种相同厚度(1 mm)，不同管径的金属管(50 mm、100 mm、150 mm)进行试验。金属管与管内线缆等长，改变金属管与线缆的长度，再改变线缆屏蔽层和芯线之间的接线方式，得到不同的实验数据。最后对集采到的数据进行耦合电压与频谱特性分析，找出规律。并用下式：

E=∑U2Δt

(16)

计算金属管内线缆耦合到的雷电流能量的一个整体趋势。

最后选取直径为50 mm的金属管在0.1 m、0.2 m、0.3 m到1 m的长度下，分别注入35 kA雷电流并采集管内线缆在屏蔽层接地情况下的耦合电压峰值，根据实际雷电流的特征拟合曲线，反推出在雷电流为35 kA情况下金属管长30 m时耦合电压的峰值。

2.2 实验数据分析

2.2.1 终端线缆开路

采用8/20 μs雷电流注入长度为1 m管径为50 mm的金属管表面，并将一根等长(1 m)的同轴线从管内中心位置穿过，同轴线一端屏蔽层与芯线开路，相当于终端负载无穷大。另外一端与示波器相连并采集线缆芯线上的耦合电压波形，典型波形见图4。整体波形上升沿时间极短，几乎小于1 μs。将前端时间轴展开，可以看出在0～0.5 μs有强烈的阻尼振荡，电压幅值较大，可能是因为在8/20 μs雷电流冲击平台触发瞬间，电磁场的瞬时变化较强烈，所以线缆耦合到的电压比较大。一般情况下，线缆耦合对后端设备造成影响产生破坏是由于能量过大所造成的，所以在采集的波形中，将整体波形开始平缓下降的点作为线缆终端电压峰值，这样可以避免及其他因素的干扰，并且与能量变化为同一趋势，后面对线缆终端电压数值读取也按照上述方式，后面将不再赘述。同轴线终端耦合到的电压与冲击电流呈正比例关系。当冲击电流为10 kA、和20 kA时，线缆终端耦合到的电压峰值分别为4.1 V和5.4 V。

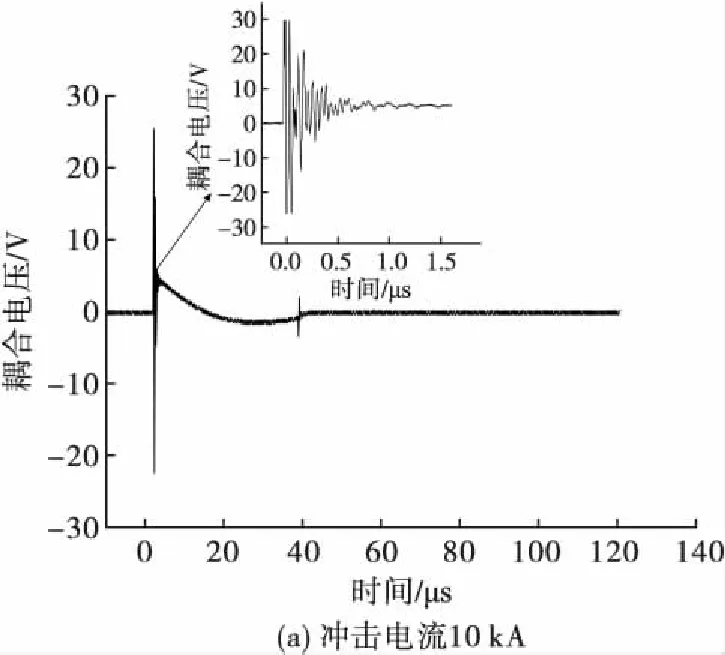
图4 终端开路时金属管内同轴线耦合电压波形

将波形上升沿阻尼振荡进行傅立叶转化，见图5。可以看出线缆耦合的雷电电磁场的频谱较宽，振幅最大集中在低频段约150 kHz左右，且随着冲击电流的增大，其振幅越大。

图5 终端开路时金属管内同轴线耦合电压频谱图

改变金属管的管径(50 mm、100 mm、150 mm),采用相同的方法测量记录终端开路的情况下，线缆终端耦合到的电压峰值见图6。由于同轴线终端开路，则示波器采集的是芯线与屏蔽层耦合的电压差，从图6可以看出终端开路情况下的耦合电压与冲击电流成正比例关系，与管径也成正比例关系，管径越大的芯线与屏蔽层的耦合电压差也越大。

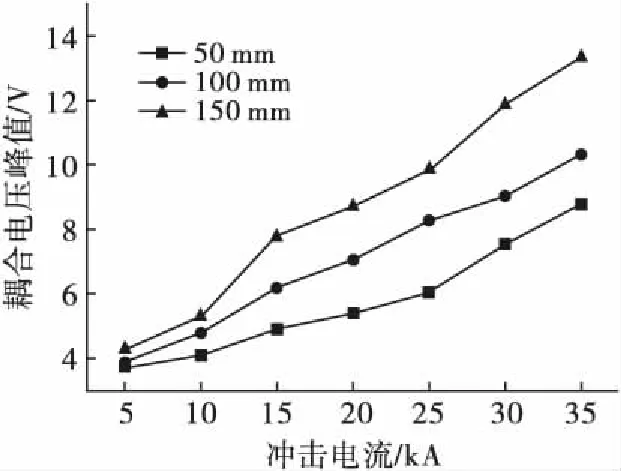
图6 终端开路时不同管径金属管内同轴线耦合电压峰值

通过公式(16)进行能量处理计算，可得不同管径金属管管内线缆终端开路时耦合到的能量趋势。见表1与图7，随着管径增大，耦合到的能量逐渐增大，耦合能量与冲击电流与管径呈正比例关系。

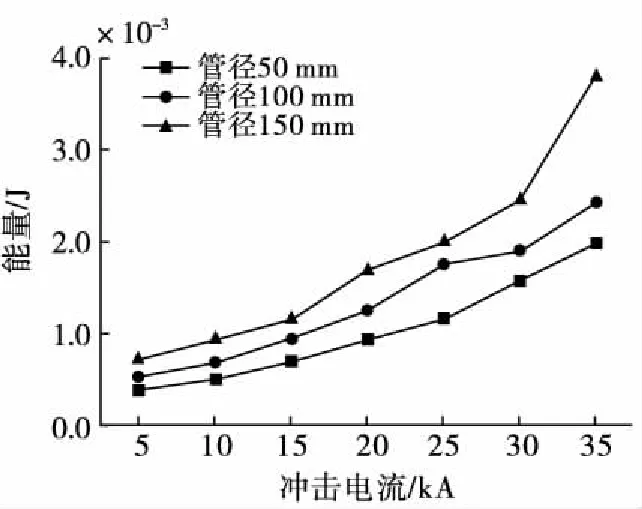
图7 终端开路时不同管径管内线缆耦合到的能量

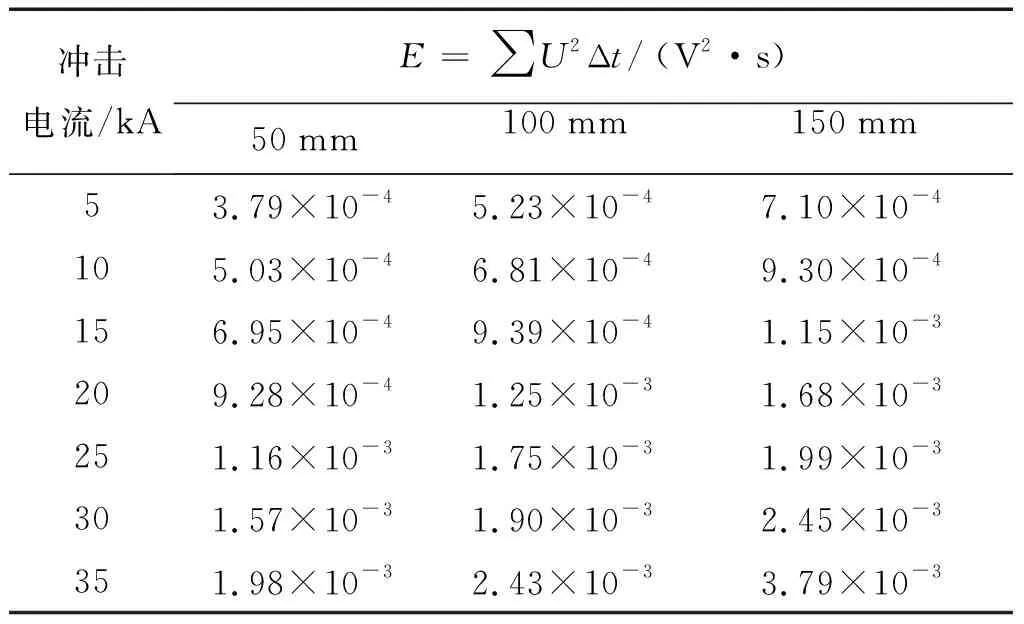
表1 终端开路时不同管径金属管内同轴线耦合能量

2.2.2 终端接50 Ω匹配电阻

采用8/20 μs雷电流注入长度为1 m管径为50 mm的金属管表面，并将一根等长(1 m)的同轴线从管内中心位置穿过，将同轴线一端屏蔽层与芯线之间接50 Ω匹配阻抗，另一端与示波器相连，采集耦合电压波形，典型波形见图8。波形与终端开路时耦合波形类似，上升沿时间极短，在0～0.5 μs强烈的阻尼振荡，电压值较大，但是耦合电压峰值较开路情况下小，因为终端屏蔽层与芯线接匹配阻抗，相当于形成了一个闭合回路，所以示波器采集到的耦合电压幅值较小。随着冲击电流的增大，终端耦合的电压也随之增大。当冲击电流为10 kA、和20 kA时，线缆终端耦合到的电压峰值分别为1.5 V和3.2 V。

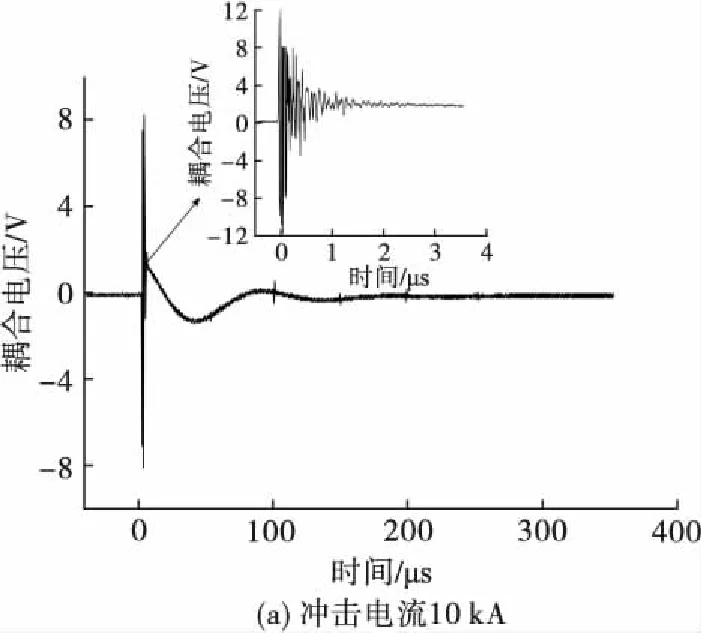
图8 终端接50 Ω匹配电阻时金属管内同轴线耦合电压波形

将采集波形的前端上升沿展开，可以看到在0～0.5 μs有强烈的阻尼振荡，电压值较大。对阻尼振荡进行频域分析，见图9。图9中其频谱特征与终端开路情况下类似，线缆耦合的雷电电磁场的频谱较宽，振幅最大集中在低频段约200 kHz～300 kHz，且随着冲击电流的增大，其振幅越来越大，但是后面的高频分量较开路时更为丰富一些，因为芯线和屏蔽层形成了一个闭合回路，回路中高次谐波造成高频分量丰富。

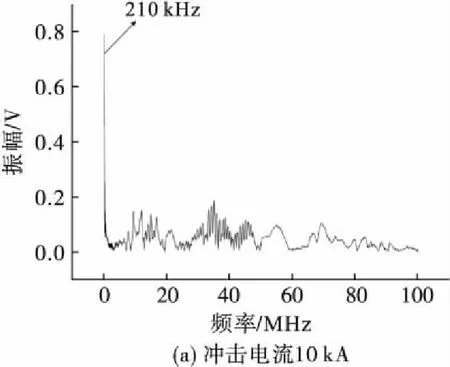
图9 终端接50 Ω匹配电阻时金属管内同轴线耦合电压频谱图

改变金属管的管径(50 mm、100 mm、150 mm),采用相同的方法测量记录终端接50 Ω匹配电阻的情况，见图10。可以看出线缆终端芯线上的耦合电压与冲击电流成正比例关系，与管径成反比例关系，管径越大芯线耦合的电压越小。这是因为终端接匹配阻抗后，芯线与屏蔽层相当于形成一个闭合回路，管径越大，管内线缆距金属管表面的距离越大，从而金属管与线缆之间形成的耦合电容越小，所以耦合电压与管径呈反比例关系。

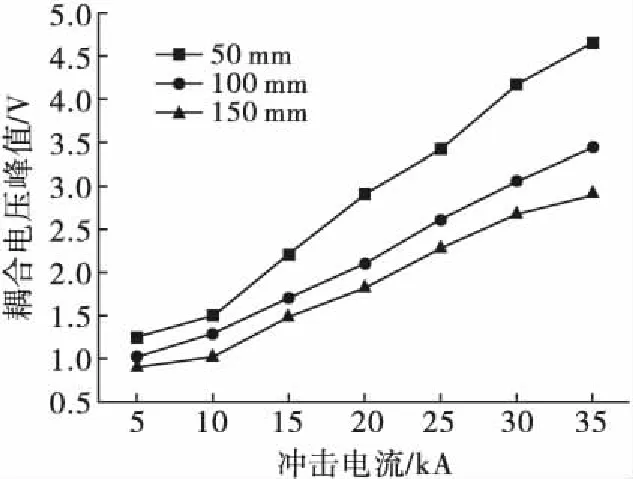
图10 终端接50 Ω匹配电阻时不同管径金属管内同轴线耦合电压峰值

通过公式(16)计算，得到不同管径在终端接50 Ω匹配电阻时耦合到的能量见表2与图11，随着管径增大，耦合到的能量逐渐减小，耦合能量与冲击电流呈正比例关系与管径呈反比例，与上述耦合电压峰值的关系一致。

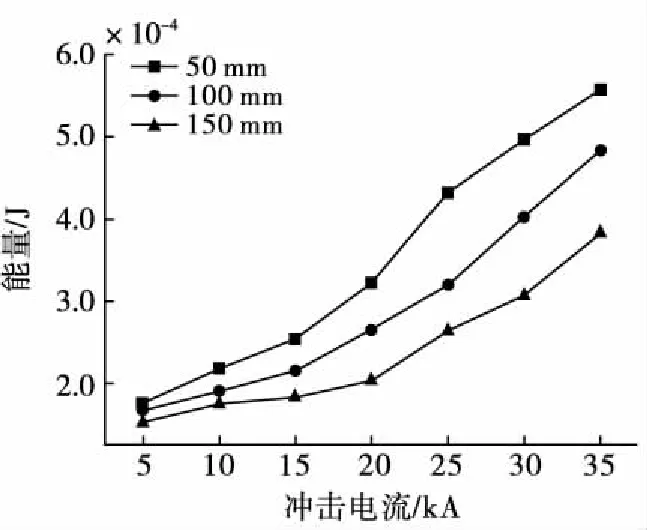
图11 终端接50 Ω匹配阻抗时不同管径管内同轴线缆耦合能量图

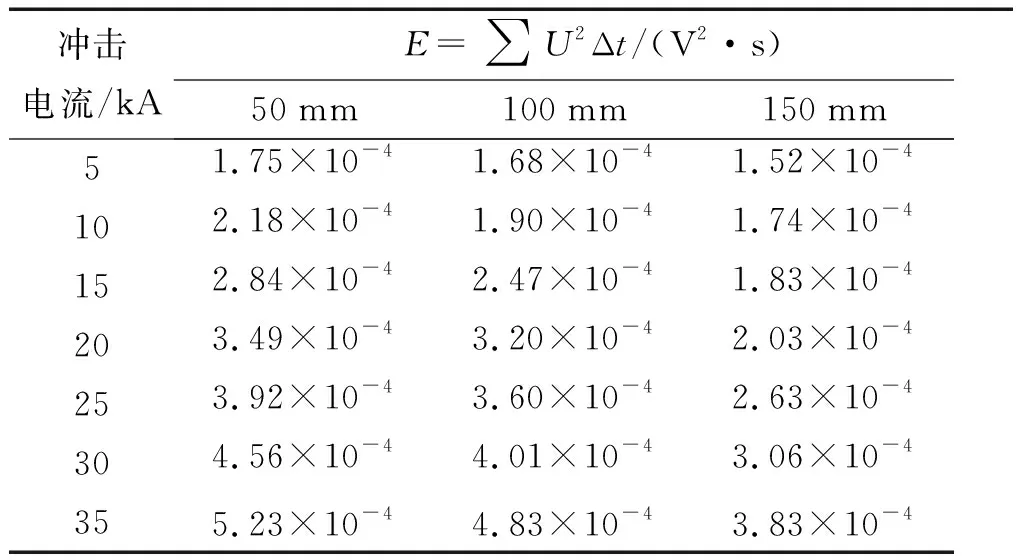
表2 终端接50 Ω匹配电阻时不同管径管内同轴线缆耦合能量

2.2.3 终端屏蔽层接地

采用8/20 μs雷电流注入长度为1 m管径为50 mm的金属管表面，并将一根等长(1 m)的同轴线从管内中心位置穿过，将同轴线一端屏蔽层接地，另外一端示波器相连采集线缆芯线上的耦合电压波形，典型波形见图12。随着冲击电流的增大，同轴线终端耦合到的电压随之增大，波形是一个完整的8/20 μs的双指数波形，并且波形前端的上升沿相比于终端开路、接匹配阻抗时，时间变长，约为10 μs左右。当冲击电流为10 kA、20 kA时，线缆终端耦合到的电压峰值分别为16.9 V和20.57 V。

图12 屏蔽层接地时金属管内同轴线耦合电压波形

对波形前端上升沿展开并进行频域分析，可以看出在0～0.3 μs有强烈的阻尼振荡，持续时间极短，电压值较大。见图13，可以看出线缆耦合的雷电电磁场的频谱较宽，振幅最大集中在1 MHz左右，相比于终端开路、接匹配阻抗时中心频率更高，高频分量最为丰富，可能是由于线缆中高次谐波引起的，中心频率大概在1 MHz左右。振幅强度与冲击电流呈正比例关系。

图13 屏蔽层接地时金属管内同轴线耦合电压频谱图

改变金属管的管径(50 mm、100 mm、150 mm),采用相同的方法测量记录屏蔽层接地的情况下，因为屏蔽层接地，屏蔽层上的耦合同轴电缆屏蔽层接地以后在屏蔽层产生的耦合电压迅速通过地线向大地释放，此时屏蔽层相当于零电位。线缆终端耦合到的其实就是芯线的对地电压，见图14。可以看出线缆终端芯线上的耦合电压与冲击电流成正比例关系，与管径成反比例关系。这是由于管径越大，芯线与金属管之间形成的耦合电容值越小，则芯线上的耦合电压越小。本研究讨论的3种情况中，终端屏蔽层接地的情况耦合到的电压峰值是最大的。

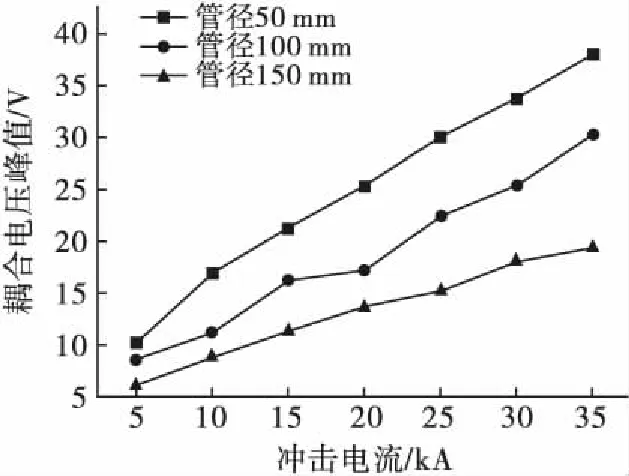
图14 屏蔽层接地时不同管径金属管内同轴线耦合电压峰值

通过公式(16)进行能量处理，得到不同管径金属管管内线缆在终端屏蔽层接地时耦合到的能量见表3及图15，管径越大，耦合到的能量越小。且同轴线终端屏蔽层接地时耦合到的能量比前面讨论的终端开路与终端加匹配阻抗到的情况下耦合到的能量大一个数量级。

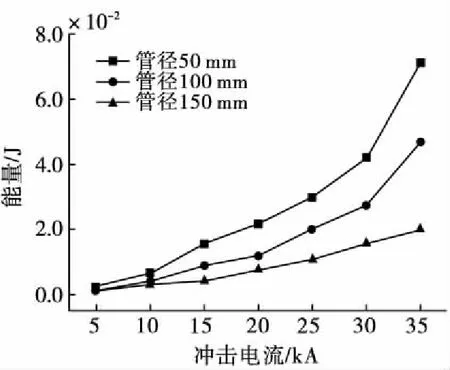
图15 屏蔽层接地时不同管径管内同轴线缆耦合能量图

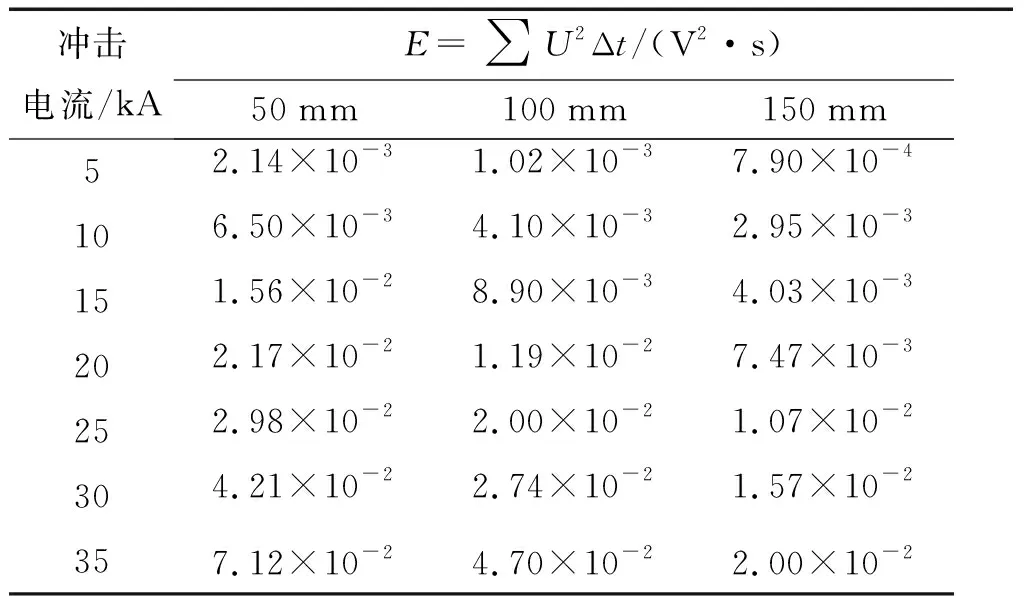
表3 屏蔽层接地时不同管径管内同轴线缆耦合能量

2.3 实际应用

在实际情况中，路灯、视频监控柱子通常在3 m～6 m，通讯塔的高度从30 m～100 m不等，因此用试验所得数据反推出实际情况中金属管内线缆耦合到的电压峰值，为后端的防雷器件的选择设计提供依据。结合实际情况，自然界中雷击电流最高约在35 kA左右，分别将0.2 m、0.3 m到1 m长管径为50 mm的金属管注入35 kA的8/20 μs波形的雷电流，采集管内线缆终端屏蔽层接地情况下所耦合到的电压峰值，并拟合出曲线。考虑到线缆传输时的衰减，采用对数函数进行拟合收敛，x轴代表金属管长度,y代表屏蔽层接地时芯线的耦合电压，最终拟合曲线为

y=54.93ln (x+2.3)-28.6

见图16，雷击电流为35 kA时，当金属管长度为30 m(x=30)，计算出线缆耦合电压约为158 V。

图16 冲击电流35 kA下不同长度金属管内线缆耦合电压

3 结论

将不同的8/20 μs冲击电流注入金属管，改变管径大小以及管内线缆不同接线方式，采集终端耦合电压波形，通过峰值、频谱以及反推试验分析，得到了以下结论：

1)金属管内同轴线缆耦合电压波形总体为双指数波，只是在0～0.5 μs间存在强烈阻尼震荡。当同轴线缆终端开路或者接50 Ω匹配电阻时，耦合到的双指数波上升沿极短，当线缆终端屏蔽层接地时，耦合到的双指数波上升沿时间加长，约为10 μs。

2)对前端的阻尼振荡进行傅立叶变化与频谱分析，发现振幅强度随着冲击电流的增大而增大。当线缆终端开路或者接50 Ω匹配电阻时，振幅最强烈的在低频段，约为150 kHz～300 kHz左右，而当屏蔽层接地的情况下，振幅最高的处在高频段，约1 MHz左右，且高频分量最为丰富，这可能是芯线中的高次谐波所引起。

3)同轴线缆耦合电压峰值与能量的变化趋势与冲击电流的变化一致。终端屏蔽层接地与终端接50 Ω的匹配电阻时，耦合电压随管径的增大而减小，这是因为随着金属管管径增大，同轴线缆与金属管间形成的耦合电容减小。而线缆终端开路时耦合电压与管径成正比例关系，随金属管管径的增大而增大。

4)利用实验数据拟合曲线，推出在实际情况中，当雷电波电流达到35 kA，管径50 mm的不同长度金属管内线缆屏蔽层接地情况下耦合电压峰值的函数为y=54.93ln (x+2.3)-28.6(x为金属管长度)，当长度为30 m时，终端耦合电压约为158 V。