动荷载条件下波浪桩力学性能分析

袁肇彦

（广东省科达水利电力岩土工程有限公司，广东 广州 510000）

1 概述

水工建筑物的设计中,常遇到建筑物地基地质条件不好、竖向承载力和抗滑稳定不满足的情况[1-5]，采用桩基础处理地基,是解决这些问题的有效措施之一[6]。波浪桩是一种新型的预制护岸结构，采用工厂化预制，离心成型，高温养护成桩。相比普通混凝土桩，其耐久性能好，其抗氯离子、抗硫酸盐、抗冻、抗渗等性能均达到国标中强腐蚀环境下100年的要求，因此在沿海的水利工程中使用广泛[7]。

目前国内学者对波浪桩的工作性能以及应用进行了相关研究。王元战等[8]采用改进Morison波浪力计算公式研究了流固耦合对桩身波浪力的影响,并给出了考虑流固耦合影响的波浪力放大系数图表；郭英等[9]针对黑龙江地区极寒地质条件进行了预应力混凝土波浪桩钻孔和沉桩设备选型试验；刘田玉[10]针对某风力发电机的钢管桩结构,考虑波浪荷载的周期性作用,计算分析了单桩式基础与上部结构的模态振型；闫彭彭[11]采用AutoBank软件对堤防各运行工况进行波浪桩稳定分析；钟可圳[12]在预应力混凝土波浪桩技术优势的基础上,针对该工程东凤镇项目区预应力混凝土波浪桩钻孔及沉桩设备的组合、施工工艺及具体施工过程等进行了可行性论证；王静[13]阐述了预应力混凝土波浪桩的结构特点；刘永利等[14]结合波浪桩护岸在沂河北岛安全生态修复项目中的应用,介绍了波浪桩的施工工艺及施工控制要点。

从以上文献分析可以得出，当前国内对波浪桩的研究主要集中于应用和施工工艺方面，少有文献对波浪桩的动力性能进行研究，而动荷载是沿海桩基设计的重要标准之一，因此有必要对波浪桩在波浪荷载和地震荷载下的动力响应进行分析。因此，本文以广东省台山市新昌水波浪桩工程为例，采用有限元软件分析了波浪荷载和地震荷载作用下，波浪桩的动力响应规律，研究成果可为相关工程提供参考。

2 工程概况

本次研究的波浪桩工程位于台山市新昌水(四九河段)，治理河道总长为10.5km，护岸11.06km，清淤疏浚总长7.0km，其中桩号S0+109—0+562段右岸共453m为波浪桩措施，波浪桩每根宽0.588m，长4m，共有770根。护岸采用雷诺护垫砌护，雷诺护垫尺寸6m×2m×0.3m，为减少岸坡渗漏，在雷诺护垫底部铺设两布一膜，规格尺寸为200g/m2，左岸岸坡顶设置7.5m宽堤顶道路,右岸岸坡顶设置6m宽堤顶道路,护岸水面以上超高部分和堤顶道路以上边坡设1.65m×1.65m砼网格梁,内填耕植土，人工播撒草籽。图1为波浪桩。

图1 波浪桩

3 数值模型

3.1 波浪压力分析

本文的数值模拟分两部分，第一部分先分析波浪桩在波浪荷载下的动力响应。因此在进行力学分析之前，首先必须知道波浪的变化规律，才能施加波浪压力。本文在计算之前通过多次现场测试先获得了波浪的波高变化规律，如图2所示。图中为测试时间约600—760s之间，其波高最高31cm，波动由不同高度、不同周期的波浪组成的，在高度和周期上存在不明显的变化规律，因此需要对测试结果进行数学处理。当前分析复杂波的主要方法有两种，频谱分析和逐波（波列）分析，本文采用更强大的频谱分析方法。假设海况可以被视为具有不同频率、高度和方向的大量规则正弦波分量的组合或叠加。也就是说，频谱分析方法通过将波记录的时间序列转换为波谱来确定每个波频率的波能量分布和平均统计信息，这本质上是从时域到频域的转换。

图2 波浪的波高变化

在获得规律变化的时频图后，开展一系列流体动力学模拟，最后得到了波动量变化图，即后期数值模拟输入的波浪压力以波动能代替，如图3所示。

图3 波动量变化规律

3.2 地震荷载分析

本次分析将0.2g、0.3g、0.4g和0.5g的地震加速度施加在来自桩基底部，施加时间2s。为了获得桩的最大响应，经过多次试验，发现2s的振动时间满足条件，因此，不再尝试进一步的时间性能分析。

3.3 模型建立

为探究一组波浪桩在波浪压力下的力学性能，本次采用有限元软件对波浪桩进行建模分析。图4为本次建立的有限元模型。图中，地基土为密砂，高8m，波浪桩每根宽0.588m，长4m，采用三角形网格划分，网格数量1 282个，材料采用弹塑性模型，波浪动力与第三节中的分析结果保持一致。至于边界条件，挡水面为应力边界，隔水面为自由表面，底板全约束。表1为数值计算参数。

图4 波浪桩数值模型

表1 模型计算力学参数

4 数值结果分析

4.1 破浪荷载下桩基响应

图5给出了波浪荷载下，桩基顶部位移变化结果。由图可知，桩基的位移呈非线性变化趋势明显，局部动荡较为明显，位移先增大后减小。桩基在6s的动荷载下，最大位移分别为0.011m，发生在2.5s的时间点上，之后回弹至0.09m。此外，从图中还可得出，即使在正弦荷载下获得了相似的最大振幅，但桩基的位移变化并非呈周期性变化，这是由于桩基产生共振效应而引起的，因此在进行波浪桩安全设计时，应当考虑桩体的共振效应，提高桩基下沉位移设计的可靠性。

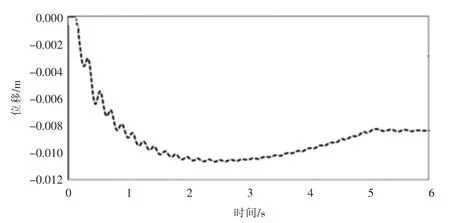
图5 波浪荷载下桩基顶部位移变化结果

4.2 地震荷载下桩基响应

了解波浪桩对地震荷载的响应对于桩体动力设计至关重要。因此，本节研究了密实砂土中桩在各种动荷载加速度（即正弦振动）下的响应（加速度、垂直位移）。为了正确模拟波浪桩和砂之间的摩擦相互作用，根据砂的相对密度定义了接触界面。此外，在桩头估算桩的动态响应（加速度、位移）。图6给出了波浪桩在地震荷载作用下加速度变化规律。研究发现，波浪桩头的加速度和位移都随着动载荷的增加而增加，振幅响应较大，能够响应0.5g至2.5g的加速度。图7给出了波浪桩在地震荷载作用下桩头位移变化规律。由图可知，随着地震加速度的增大，桩的位移同样出现增大的趋势，但最大位移峰值时间具有一定差异，在密实砂中桩产生的最大位移范围为0.1m至0.5m。

图6 波浪桩在地震荷载作用下加速度变化规律

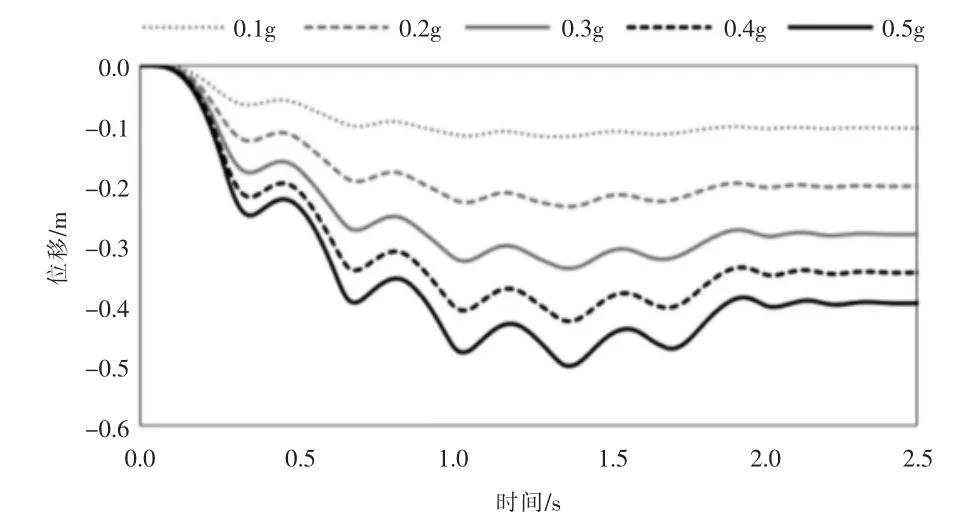
图7 不同水位下液压坝的位移变化规律

5 结论

本文以广东省台山市新昌水波浪桩工程为例，采用有限元分析软件分析了波浪荷载和地震荷载作用下，波浪桩的动力响应规律。研究结果表明，波浪荷载作用下，桩基的位移呈非线性变化趋势明显，位移先增大后减小。桩基在6s的动荷载下，最大位移分别为0.011m，发生在2.5s的时间点上，之后回弹至0.09m。另一方面，在地震荷载作用下，波浪桩头的加速度和位移都随着动载荷的增加而增加，振幅响应较大，能够响应0.5g至2.5g的加速度，桩产生的最大位移范围为0.1m至0.5m。研究成果可为工程提供参考。□