美式多资产期权定价问题的格子Boltzmann方法

李 聪，武芳芳

(沈阳工业大学 理学院，沈阳 110870)

格子Boltzmann方法[1-2]自提出之日起，便迅速发展成为流体力学、数学、物理学等相关领域内的研究热点.格子Boltzmann方法基于分子动力学理论而建立，与传统数值方法不同，它具有清晰的物理背景，其时间、空间完全独立，边界易于处理，是一种完全并行化的介观模拟算法.格子Boltzmann方法的独特优势使其在求解各类非线性偏微分方程数值解[3-7]方面克服了许多传统算法的不足，受到众多专家学者的广泛关注，发展前景日益广阔.

期权[8-9]是金融领域中一种风险管理的核心工具，多资产期权作为一种奇异期权[10]，由多个风险资产组成.美式多资产看跌期权满足下列线性互补模型[8]：

(1)

终值条件为V(S,T)=φ(S)，其中

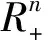
1 有界区域上的定价模型

通过变量替换t=T-τ，xi=lnSi，u(xi,τ)=V(Si,t)(i=1,2)和惩罚法[17]将方程(1)转化为下列等价方程

(2)

假设截断区域是Ω=[-l1,l1]×[-l2,l2]，其中li(i=1,2)是未知变量，对于固定时间t∈(0,T]，固定点(x1,x2)∈R2以及给定充分小的数ζ∈(0,1)，由远场截断法[18-19]可知截断长度lmax满足以下关系

(3)

且有lmax≤li，K表示敲定价格.

2 格子Boltzmann模型

格子Boltzmann模型是基于DnQb系列速度模型(其中n表示空间维数，b表示离散速度)的单松弛格子BGK(Bhatnagar-Gross-Krook)模型[20].方程(2)的格子Boltzmann模型的局部粒子分布函数演化方程为

(4)

对方程(4)做Taylor展开，有

(5)

再实施以下多尺度Chapman-Enskog展开[22]，

(6)

其中ε是Knudsen数[23].将式(6)代入方程(5)中，对比ε的各阶系数，可得

(7)

(8)

(9)

(10)

定义宏观量u(x,t)为该点各个方向的局部粒子分布函数的和，即

(11)

由于质量守恒，故局部平衡态分布函数满足

(12)

因此由方程(7)和式(12)，有

(13)

为恢复宏观方程(2)，对局部平衡态分布函数做如下限制，

(14)

同时对补偿函数做如下限制，

(15)

由式(6)(15)，可得

(16)

(17)

对方程(8)关于α求和，并结合式(13)(14)(16)和(17)有

(18)

对方程(9)关于α求和，并结合式(13)(14)(16)和(17)有

(19)

对方程(10)关于α求和，并结合式(13)(14)(16)和(17)有

(20)

2.1 D2Q5模型

对方程(2)采用D2Q5速度模型，其离散速度集合为{eα,α=0,1,…,4}={(0,0),(c,0),(-c,0),(0,c),(0,-c)},由式(18)×ε+(19)×ε2可以恢复得到具有二阶精度的宏观方程

(21)

为恢复方程(2)，令

则方程(21)可变为

由式(13)(14)可得一组平衡态分布函数为

由式(15)(16)(17)可得一组补偿函数为

2.2 D2Q9模型

对方程(2)采用D2Q9速度模型，其离散速度集合为{eα,α=0,1,…,8}={(0,0),(c,0),(-c,0),(0,c),(0,-c),(c,c),(-c,c),(-c,-c),(c,-c)}，由式(18)×ε+(19)×ε2+(20)×ε3可以恢复得到具有三阶精度的宏观方程

(22)

为恢复方程(2)，令

则方程(22)可变为

由式(13)(14)可得一组平衡态分布函数为

由式(15)(16)(17)可得一组补偿函数为

3 数值模拟

为验证本文算法的有效性，考虑1年期美式多资产期权定价模型，即T=1，取敲定价格K=1，σ1=0.2，σ2=0.3，q1=0.05，q2=0.01，在线性互补模型(1)中取终值条件φ(S1,S2)=max{K-α1S1-α2S2,0},其中αi≥0(i=1,2)表示第i个标的资产所占比例，且有α1+α2=1，故取α1=0.6，α2=0.4.在数值模拟过程中，初始粒子分布函数取平衡态分布函数，采用非平衡外推格式[24]处理边界条件，同时定义全局误差为

其中u(xi,xj,t)表示数值解，u*(xi,xj,t)表示精确解.

在式(3)中取ζ=10-5可得截断长度lmax=2.082 5，为叙述方便取l1=l2=lmax/2，故截断区域为Ω∈[-1,1]×[-1,1].

在数值模拟过程中，时间间隔取Δt=0.001，空间步长取Δx=2/N，N为格子数，松弛时间取τ=2.5，惩罚法系数取η=0.01.取格子数N=200.图1和图2分别描绘了D2Q5模型和D2Q9模型在3组无风险利率r=0.05，r=0.10和r=0.20下T=1时刻的期权价格.参照文献[15]中有限元法得到的期权价格图像，图1和图2中期权价格图形与其形状相吻合，证实了本文所建立格子Boltzmann模型的有效性.

(a) r=0.05 (b) r=0.10 (c) r=0.20图1 D2Q5速度模型下的期权价格Fig.1 Option prices of LBM under D2Q5 model

(a) r=0.05 (b) r=0.10 (c) r=0.20图2 D2Q9速度模型下的期权价格Fig.2 Option prices of LBM under D2Q9 model

由于美式多资产期权定价问题不存在显式解，取D2Q9速度模型在格子数N=800以及T=1时刻下的数值解作为精确解u*(xi,xj,t)的近似.表1列出了D2Q5速度模型和D2Q9速度模型在不同无风险利率下的全局误差.图3描绘了在不同无风险利率下的全局误差图像，图像表明在同一速度模型下格子数越大，误差越小；在相同无风险利率下D2Q9模型比D2Q5模型误差更小.

表1 D2Q5和D2Q9速度模型的全局误差Tab.1 Global relative errors under D2Q5 model and D2Q9 model

(a) r=0.05 (b) r=0.10 (c) r=0.20图3 D2Q5和D2Q9速度模型下的全局误差图Fig.3 Diagrams of Global relative errors under D2Q5 model and D2Q9 model

4 结论

本文实现了利用格子Boltzmann方法求解美式多资产期权定价问题.利用惩罚法和远场截断法将无界区域上的线性互补模型转化为有界区域上的抛物问题，针对转化后的模型进行多尺度Chapman-Enskog展开等一系列计算，同时确定不同速度模型下的平衡态分布函数和补偿函数，最终计算得到期权价格.数值模拟结果表明，在相同的速度模型下随着格子数的增加，误差越小；随着速度方向的增加，误差越小；并与其他数值方法做对比，期权价格图形吻合.证实了格子Boltzmann方法对于研究美式多资产期权定价问题是一种有效算法,该算法为求解美式多资产期权定价问题提供了新思路.