从“数学活动”探索中获得数学“再发现”——以人教版八年级下册数学活动“折纸做60°,30°,15°的角”为例

倪方友

(云南省昆明市滇池度假区实验学校,650228)

“数学活动”是为了落实课程标准提出的基本数学活动经验的积累,是实施“综合与实践”的知识领域.教师通过问题引领,引导学生自主全程参与的活动过程,体现数学教学的活动性、综合性和探究性的要求.“平行四边形”章节的重点是突出图形性质定理和判定定理的探索与发现过程,由观察度量、实验操作、图形变化等方式,培养学生的合情推理和演绎推理能力.下面笔者以人教版八年级下册“平行四边形”章节中数学活动“折纸做60°,30°,15°的角”为例,谈谈挖掘“数学活动”的教育价值,发展学生的问题意识和创新意识.

一、数学活动内容与活动设计

1.折纸做60°,30°,15°的角

如果我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,可以采用下面的方法(如图1):

(1)对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平.

(2)再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM.同时,得到了线段BN.

观察所得的∠ABM,∠MBN,∠NBC,这三个角有什么关系?你能证明吗?

通过证明可知,这是从矩形得到30°角的好方法,简单而准确,由此,15°,60°,120°,150°等角就容易得到了.

2.数学活动设计

(1)活动准备:让学生准备好一张矩形纸片,三角板,量角器,笔;

(2)活动过程:学生分小组按活动步骤动手实践折纸,学生自主探究并度量出折出的角度的大小,并证明折出的角度的度数,小组内合作交流自己的想法;

(3)分小组在全班进行展示活动的结果.

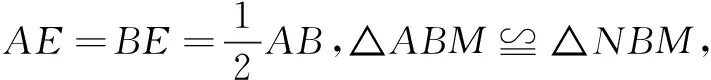
二、活动后的数学“再发现”

折纸活动完成后,教师对活动进行延伸和追问,通过问题引领激发学生更深入的思考,引导学生关注数学前后知识之间的联系,形成数学的整体观念,体现数学知识的综合应用,进一步培养学生的探究能力.由已知条件执因索果而来的结论,通过关联式的追问,递进式的延伸和发散式的拓展,对活动进行深入地探究和挖掘,以得到进一步的发现,找到题目的固有结论和点线之间的位置关系和大小关系,提升学生提出问题、发现问题、分析问题和解决问题的能力(2020年昆明市中考数学压轴题第23题就是基于折纸活动的数学“再发现”的思想而命制).

1.基本模型再现

模型1如图2,点E,F分别为矩形ABCD的边AB,CD的中点;你能得到什么结论?并证明.

模型2如图3,点P是边AD上的一点,将ABP沿BP对折,点A落在矩形内部一点M处.你能得到什么结论?并说明理由.

结论猜想:对给出的基本图形及题目中的已知条件,猜想出可能得到的结论,并证明猜想的正确性.

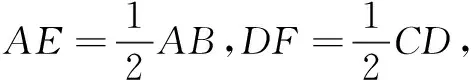
模型2由轴对称的性质可得ABP≌MBP,从而可得AB=MB,PA=PM,∠M=∠A=90°.(理由略)

2.关联式追问

在原有两模型的图形和条件的基础上，对部分图形的关系进行追问或叠加后，再探图形的关系.

追问1在模型2中,如果点P在边AD上运动,你能猜想点M的轨迹是什么吗?

追问2模型1和模型2叠加:如果点M恰好落在线段EF上,你会有什么发现?

分析因为点M到点B的距离不变,即到定点的距离等于定长的点在圆上,所以点M在以A为圆心,AB为半径的一段弧上(如图4).

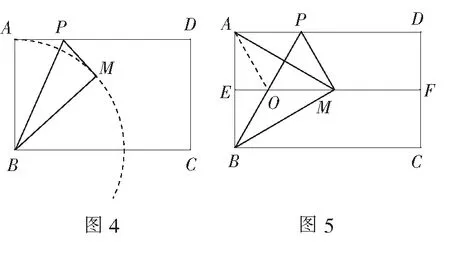
如果点M恰好落在线段EF上(如图5),就是我们在折纸活动中得到的图形,可以得到以下结论:(1)∆ABM是等边三角形,从这个结论我们还可以得到折叠等边三角形或30°角的方法;(2)OB=OM;(3)BP是线段AM的垂直平分线;(4)∆POM是等边三角形.

结论OB=OM的证明有如下方法:

方法一如图5,连结AO.由对折可以得到BP是AM的垂直平分线,可得AO=OM,由四边形AEFD为矩形,容易得到EF是AB的垂直平分线,从而有AO=BO,所以BO=OM.

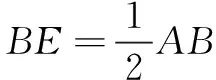
3.递进式延伸

通过上面的探索,我们可以在原有图形模型上通过增加条件或添加线段得到一个在原有的图形基础上递进式的图形,再探究该图形的性质和结论.

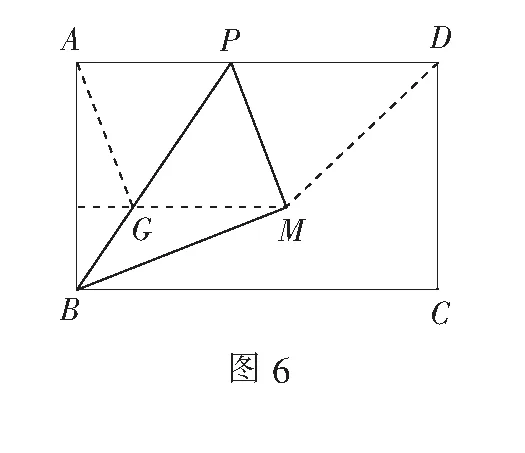
延伸1如图6,作MG∥AD交BP于点G,请判断四边形AGMP的形状.

延伸2如图6,如果AB=5,BC=8,连结DM,是否存在DM的长度最小?如果有,请求出最小值?

4.发散式拓展

在上面的题目现有条件基础上进行发散式拓展,对图形进行延伸,对前后知识进行综合,提升学生的思维层次,从而培养学生的探究能力和创新意识.

拓展:如图7,AB=5,BC=8,当点P在直线AD上运动时,如果∆AMD为等腰三角形,请求出AP的长.

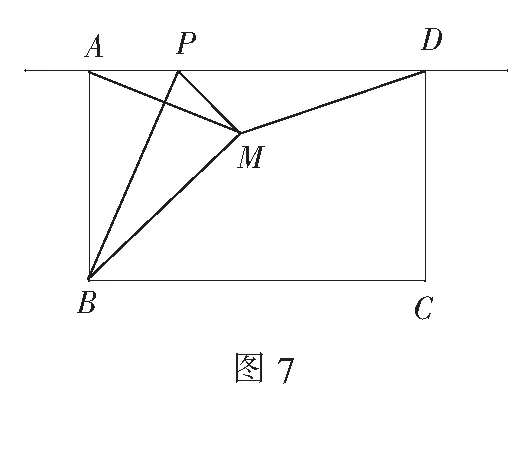
这样拓展以后,题目的难度更大,能考查学生的探究能力、几何直观能力、空间想象能力、运算能力、分类讨论思想和化归思想.通过分析,我们发现有五种情况:

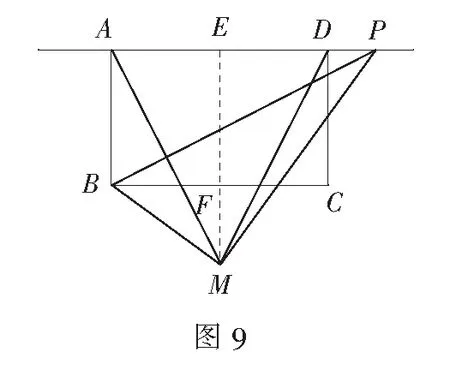
情况2当MA=MD,点P在边AD的延长线上时(如图9),过点M作ME⊥AD于E,交BC于F,同理可得MF=3,从而得ME=8,设AP=PM=x,PE=x-4，由勾股定理得(x-4)2+82=x2，解得AP=10.

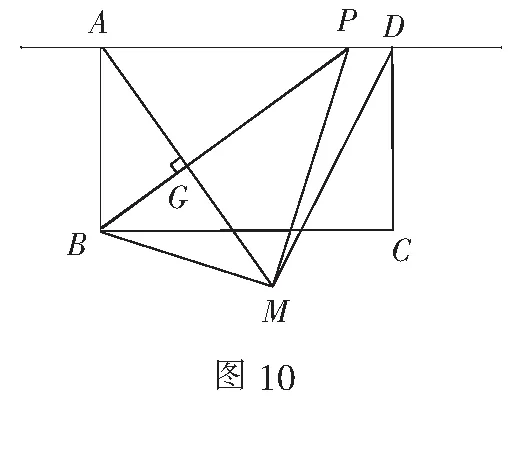
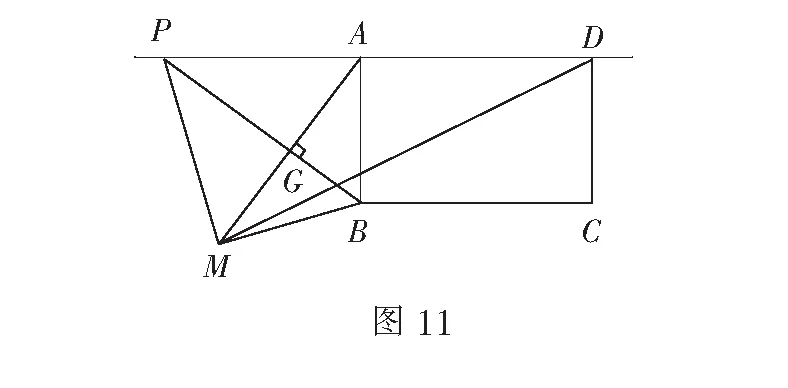
情况5当DA=DM,此时点P与点D重合(如图12),得到AP=AD=8.

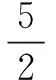
5.探究反思

通过对折纸活动进行不同角度的探索,我们获得一些解题方法、数学活动经验和重要启示:

启示1通过折纸可以获得等边三角形的方法.(1)对折矩形纸片ABCD,使得AD与BC重合,得到折痕EF,把纸片展平.(2)再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM.同时,得到了BN,从而∆ABM是等边三角形.

启示2在动点问题中,一个点的位置随另一个点的位置变化而变化,该点的轨迹可循,比如本题点M的轨迹是圆弧,强化对图形的基本性质和概念的理解.

启示3拓展题目是一个关于构建等腰三角形分类讨论的题型,基本方法是分成三种情况进行讨论.本题也可以这样探究,如图13,因为点M在以B为圆心,BA为半径的圆上,要使∆AMD为等腰三角形有三种情况:第一,点M是AD的垂直平分线与⊙B的交点,得到M1和M2;第二,点M是以A为圆心,AD为半径的圆与⊙B的交点,得到M3和M4;第三,点M是以D为圆心,AD为半径的圆与⊙B的交点,得到M5.

三、结语

数学活动是帮助学生积累数学活动经验,不但要让学生经历相对完整的活动过程,教师还要进行深入挖掘,让学生经历活动后的数学“再发现”过程.让学生勇于探索一些开放性的、非常规的实际问题与数学问题,体会数学知识之间的联系,在探索数学问题解决蕴含的数学规律过程中,发现问题和提出问题,并运用数学知识与方法分析问题和解决问题.