基于多元统计分析的双电磁比例方向阀故障诊断

朱鑫达，刘超，王俊奇，刘振

(1. 江苏大学，江苏 镇江 212013； 2. 镇江四联机电有限公司，江苏 镇江 212000)

0 引言

随着我国大型制造产业的兴盛发展，故障诊断和质量检测越来越被重视，且被视为是保障生产线安全与质量的重要技术支持手段。阀类控制技术在液压伺服系统中起着举足轻重的作用。双电磁比例方向阀是比例技术与电磁技术结合的产物，采用该类阀可以提高系统的自动化程度，又简化了系统，是液压伺服系统的重要元件组成之一。但由于双电磁比例方向阀工作环境恶劣，其发生故障的频率较高[1]。一旦损坏，易造成巨大的经济损失。因此对双电磁比例方向阀进行有效且迅速的故障诊断和维修具有重要的现实意义[2]。

国际故障诊断理论权威FRANK P M教授最早提出将故障诊断方法分为3类：基于知识的方法、基于解析模型的方法和基于信号处理的方法[3]。如今已开发了多种故障诊断模型来检测阀类的故障，如多重统计分析法、正态分布检验、BP神经网络、支持向量机、模糊诊断等[4]。袁兵等利用维数缩减技术和模糊减法聚类法，实现了自适应神经-模糊推理系统(ANFIS)的结构辨识，并建立了适用于电液伺服阀故障模式识别的ANFIS，从而有效地解决了电液伺服阀故障多样性和不确定性的难题，实现了电液伺服阀故障的智能诊断[5]。然而在大规模数据集及故障情况更为复杂的状态下，其对于确定最佳模糊参数，时间开销较大。因此本文依据文献[6]PCA的概念，提出了一种由多元统计分析开发的RPCA算法诊断模型。在原始算法训练之前设置根节点的阈值，并通过设定训练过程中的决策规则，来寻求测试误差最小的最优解。该算法模型使用简易方便，时间开销合理。通过对比原始PCA算法，表明现有开发模型的精确性和优越性。

1 双电磁比例方向阀的工作原理及常见故障研究

1.1 双电磁比例方向阀工作原理

在种类繁多、运用广泛的比例方向阀中，本文以双电磁比例方向阀作为研究对象，其结构如图1所示。它主要由电与磁两部分组成。它的构成结构分别是位移传感器、比例电磁铁、两端弹簧、弹簧座、阀芯以及阀套[7]。

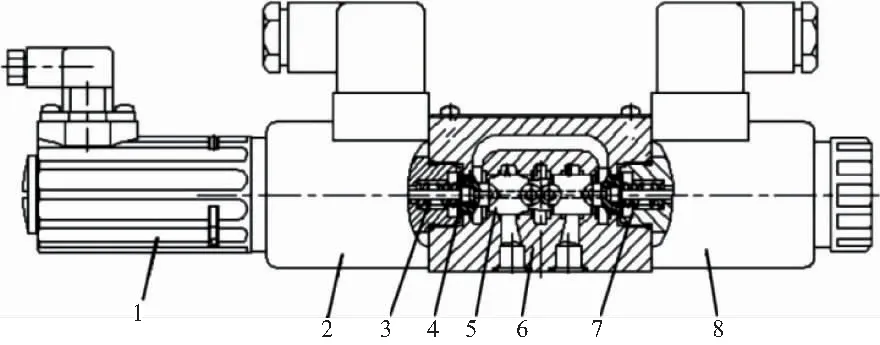
1—位移传感器；2—比例电磁铁A；3—弹簧A；4—弹簧座；5—阀心；6—阀体；7—弹簧B；8—比例电磁铁B。

当双电磁比例方向阀输入控制电流为0时，主阀芯由于受到比例电磁铁以及两端弹簧反馈的作用位于中位，此时电磁比例方向阀无流量和压力输出。

对比例阀阀心进行受力分析, 得到动力学方程为[8]

MXV=FmA+FKA-FmB-FKB-Ff-Fb-Fy

(1)

式中：FKA、FKB为左右弹簧力；FmA、FmB为左右电磁铁输出的力；Ff为摩擦力；Fb为阻尼力；Fy为液动力；M为阀心质量；XV为阀心位移。

比例阀一般采用的控制策略如图2所示。

图2 比例方向阀控制示意图

当输入电流信号发生改变时，重复上述过程，直至达到新的平衡。

1.2 双电磁比例方向阀的常见故障类型

双电磁比例方向阀的空载流量特性曲线能够反映它的大部分故障，它不仅表明了其流量增益、滞环、零偏、线性度和对称性等，更重要的是它反映了双电磁比例方向阀零位特性的类型及阀芯与阀套之间的配合性能。阀芯、比例电磁铁的磨损也能在空载流量特性曲线中很明显地反映出来[9]。故障分类检测也是基于PCA算法的故障诊断的第一步[10]。

该类阀故障类型主要包括电磁故障和机械液压故障两类。其主要故障及表现形式如表1所示[11]。

表1 故障类型表

1)磨损

电磁比例方向阀的磨损主要包括比例电磁铁磨损、两侧弹簧以及阀芯和阀套磨损。以上这3种磨损大都是由于油液污染引起。主阀芯的磨损对伺服阀零位机能会产生一定的影响，例如零位泄漏量加大、零位稳定性下降、流量增益减小、非线性加大、滞环变大等现象，磨损严重时会使伺服阀严重滞后，动态特性也将急剧下降。图3(a)为正常工作情况下(非理想)的双电磁比例方向阀空载流量特性曲线，图3(b)为该类阀在阀芯和阀套磨损情况下的空载流量特性曲线图。与图3(a)相比，可以看出，该阀滞环偏大，非线性偏大。图3(c)为双比例电磁铁退磁情况下的空载流量曲线。

2)阀芯卡死、卡滞

这类故障主要由于油液污染所致。当比例阀阀芯卡死时，比例阀完全失效；当阀芯卡滞时，比例方向阀流量特性曲线不再平滑，而是呈现一定的跳跃性，阀压力增益明显减小，比例方向阀响应性和稳定性均大幅度下降，阀处于即将报废状态。图3(d)阀输出流量接近0，最大值为0.05 L/min。

3)阀芯一端限位

这种故障一旦出现，双电磁比例方向阀阀芯只在一端运动，导致一端输出正常，另一端无信号输出。图3(e)为阀仅有正向流量输出。

4)放大板损坏

这类故障是一种机电故障，这种故障下也会导致双电磁比例方向阀没有响应出现。从图3(f)也可以看出。

图3 故障曲线图

以上机械液压故障中1)-3)大都是由于高温、油液污染引起的，电气故障中主要由于机电部位损坏产生。除了故障4)主要由于机电部件受高温、高频率或外力受损外，由故障1)-3)可见，控制油液的污染程度可以在很大程度上降低伺服阀发生故障的机率。

2 双电磁比例方向阀的故障分类建模

2.1 主成分分析方法基本原理

主成分分析方法(principal component analysis，PCA)又被称为主量分析，是目前运用最广泛的大数据规约算法，特别是对于大型稀疏矩阵，结果处理非常好[12]。其主要思想在于利用降维的方式,把数据中的多个指标处理为较少的几个综合性指标。从统计学意义上来讲,主成分分析法是一种将数据集进行简化的线性变换,在这个过程中,原始数据被变换到一个新的坐标系中。在该系统中,所有数据方差最大的方向构成第一个坐标轴,也称为第一主成分；与第一个坐标轴正交的平面中使得方差最大的方向构成第二个坐标轴,称为第二主成分,之后以此类推。通过主成分分析技术处理后,保留低阶主成分,忽略高阶主成分,即可以有效减少数据集的维数,同时保持对数据集方差贡献最大的特征,最终实现对数据特征的降维处理[13](图4)。

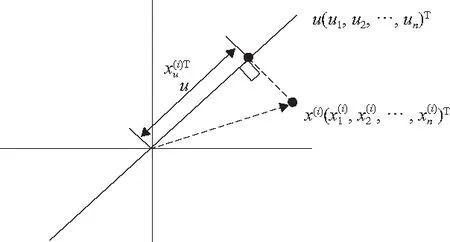
图4 数据降维映射

主成分分析法信号分解是指设定k个N维的新变量[y1，y2，…，yk],来构成线性表示的n维初始变量[x1，x2，…，xm](m≥k)，使得新变量的方差最大或者降维损失最小，如下式：

(2)

式中系数ai=(ai1，ai2，…，aim)T，i=1，2，…，k是协方差矩阵C中降序排列的第i特征值λi对应的特征向量，且ai满足式(3)：

(3)

并将式(2)改写为分量形式，有

(4)

其中yi∈Rn，i=1，2，…，k。

而协方差矩阵C的特征方程为

Cai=λiaj

(5)

以上关键便是有效主元个数的确定，取定某个或某几个阈值的方法选择有效主元的个数，选取的主元成分越多，能够更方便处理的信息就越多。

患病决策树如图5所示。

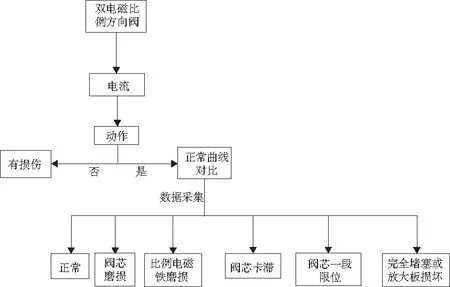
图5 是否患病决策树

依据图5所示决策树规则，由RPCA算法得到的数据是降序排列，与原始PCA算法相比，可以减少大量的顺序查找时间，时间开销少。

2.2 双电磁比例方向阀的故障分类实现流程

本文提出一种改进的RPCA算法用于方便地分析处理一类双电磁比例方向阀的故障分类，该方法的具体实现流程如图6所示。

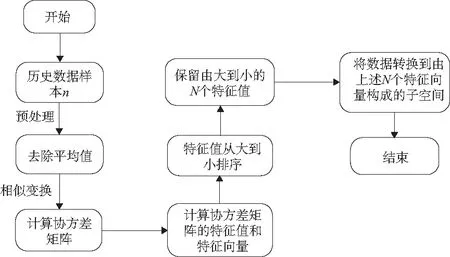
图6 算法流程图

通过预处理得到的数据不仅具有离散值,还具有连续值。具备连续性属性的数据需要离散化处理，进行离散化数据预处理后进行根节点属性选择；计算数据集中所有属性的信息增益率，选择其中的最大值属性作为根节点属性[14]。

算法相关定义概念如下：

定义1：信息熵。设X是含有n个训练样本的数据集。信息熵计算公式为

(6)

式中：m是类别数；pi是类别i出现的概率。信息熵越大，不确定性就越大。

定义2：信息增益。对于数据集X中A的信息增益为

(7)

式中A的取值为a1，a2，…，aj。这些信息增益可以衡量信息的混乱度和复杂度。

定义3：信息增益率。

(8)

信息增益率使用“分裂信息”值，最后将信息增益规范化[15]。

目标实现基本步骤为根据基本定义分别计算出训练数据集X的信息熵、信息增益以及信息增益率，通过对这些值进行比较后进入下一步操作。

1)数据集X中的数据不仅有连续数据，还有离散数据，通过计算出来的信息熵与信息增益确定节点属性，然后根据节点属性的不同建立分支，分支中的子数据集同样根据这样的规则建立新的分支。

2)根据规则进行分类预测。根据各分支上属性取值的获取，新数据集根据规则进行分类预测。

以PCA建模的方式，根据过程变量的正常历史数据，首先利用相似变换将包含原始多变量间相关性信息的协方差矩阵转换为具有对角形式的特征矩阵；然后对特征值大小进行降序排列。

通过PCA降维得到的数据是降序排列的，这样可以省略计算信息增益时的多次顺序查找，提高效率，节省时间。

3 实例探究

图7所示的阀测试台用于数据采集，PCA安装在伺服阀测试台上，由阀类静态测试仪控制。通过计算机显示电液比例伺服阀的空载流量特性曲线并保存数据。共采集5种状态下60台双电磁比例方向阀的空载流量特性曲线数据，每一组数据都包含了所采集比例方向阀的电流值与所对应的流量值、电压值以及内漏值，每项类别以3∶1∶1来选取，并设置相应的类别标签。其中实验器材有：双电磁比例方向阀、阀测试平台、阀类静态测试仪和计算机。

图7 阀类数据采集系统结构示意图

本文首先对影响两种算法准确性的节点进行实验分析，找出适用于双电磁比例方向阀故障诊断的PCA算法输入参数。最后对普通PCA算法和RPCA算法作对比性试验。

在相同实验环境下进行对比试验。为了方便，将改进的算法记为RPCA，对比算法名称不作修改。

对收集的数据进行归一化，获得算法的输入Xj，并将相应的类别标签tj用作本文模型的输出。

算法的参数设置为：进化的代数maxgen为300;种群的规模sizepop为30；选择概率pselect为0.9;交叉概率pcross为0.5;变异概率pmutation为0.7。优化后的c和g设置为c=0.32,g=32.36。比较两种算法的有效决策时间，如图8-图10所示，图中S1为RPCA模型，S2为PCA模型。

第一组实验，当保持计算节点数量一定时，对两个不同规模的数据集进行分别，然后根据决策规则执行算法，其运行时间比较结果如图8所示。

图8 不同规模数据集下算法决策的时间性能

由图8可知，数据集规模越大，基于本文RPCA算法决策规则的运行时间控制越好，时间收敛性能越好。

第二组实验，在相同的数据规模集和保持一定的时间节点的状态之下，基于两种算法规则下的时间加速比，如图9-图10所示。

图9 使用不同节点时的加速比

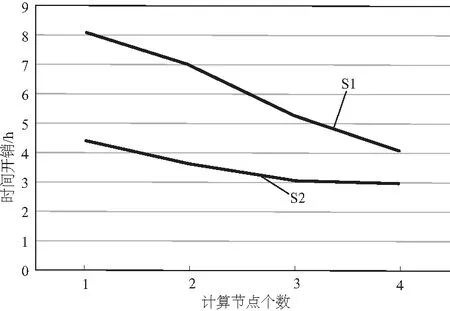
图10 使用不同节点数量时的时间

由图9-图10可知，数据集的规模越大，基于RPCA算法决策下的运行时间控制得越好，且能获得更好的时间收敛性能；同时随着决策规则下计算节点的增加，提高了系统的加速比，降低了时间开销。随着数据集规模趋势增大，其算法决策趋势越明显。表2为两种算法诊断实验的对比。

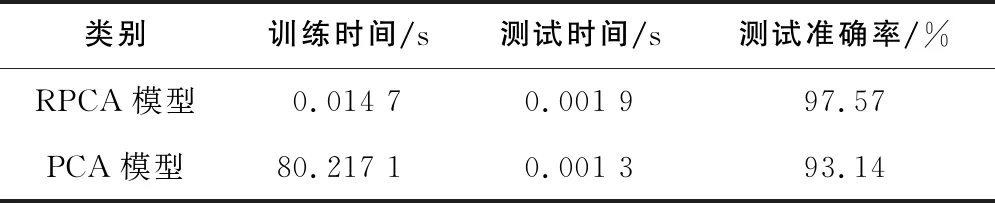
表2 诊断实验对比

表2数据表明，用RPCA模型进行电液伺服阀故障诊断，测试集准确率达到97.57%，同时，训练速度比原始算法的训练速度快数千倍。由于样本数量少，各模型的测试时间少，差异小。可见，RPCA模型的精度不仅高于原始模型，而且RPCA模型的训练时间也远少于原始模型的训练时间。由此可以看出，在电液伺服阀故障诊断中，RPCA具有更好的性能。

4 结语

本文通过建立基于改进PCA算法中信息增量的模态划分和故障检测的方法，在进行数据分析之前，首先利用算法对数据进行有序降维，通过设置合理阈值将数据降到合理维数，得到质量较高的数据。然后利用算法规则，最终对数据进行分类。经过实验表明：本文算法决策分类的准确率得到提高，所建立的模型精度较高，故障检测的速度较快。该方法大大节省了诊断时间，更加精准地确定故障部位，降低了对于双电磁比例方向阀及所应用的系统的伤害，在阀类故障诊断实际应用中具有重要意义。