一种共振型超声椭圆振动超精密刀架的设计分析

房元，胡高峰，戚厚军，贾传明

(1. 天津职业技术师范大学，天津 300222； 2. 天津市高速切削与精密加工重点实验室，天津 300222)

0 引言

20世纪90年代Shamoto和Moriwaki教授等提出了一种崭新的加工技术——超声椭圆振动切削(ultrasonic elliptical vibration cutting，UEVC)技术。该技术的原理为：刀具以额定切削速度进给的同时可以产生椭圆轨迹的高频振动。在椭圆振动切削过程中，刀具和加工工件之间不仅会发生周期性的接触与分离，而且当刀具的振动速度大于切削速度时，刀具和切屑之间的摩擦力方向发生逆转，有利于切屑的流出。超声椭圆振动切削技术相比于传统加工方式赋予其自身诸多优点，包括减小切削载荷[1]，减少后刀面磨损[2]以及在材料的去除过程中抑制毛刺的生成[3]，提高加工精度[4]，增强切削稳定性，增加刀具寿命[5]等。超声椭圆振动切削技术对世界制造业的发展影响深远，经过大量的实验验证，发现其对一些硬脆难加工材料的加工效果显著，比如淬火钢[6]、碳化钨、多晶硅和陶瓷等。目前超声椭圆振动切削技术已经成功应用于超精密加工领域。

近年来，超声椭圆振动切削装置设计受到众多业内学者的深度研究。李华等[7]提出在刀杆输出端加大质量的刀具，构成非对称结构，从而使刀具产生纵振和弯振，进而复合成椭圆振动。王跃[8]利用两组换能器同相和异相的驱动使得两正交连接的变幅杆产生纵振和弯振形成椭圆振动，并经过了实验验证。GUO P教授等[9]设计了一种具有共振模态的二维工作头，利用两个夹角为60°的郎之万换能器驱动工作头产生纵振和弯振。KURNIAWAN R等[10]研制了一种基于夹层式压电驱动器的三维UEVC装置，通过两组半圆形压电陶瓷和一组圆形压电陶瓷驱动变幅杆，构成弯-弯-纵振动模态，可实现三维超声椭圆振动。对于以上双激励或多激励驱动的UEVC装置，其结构的设计过于复杂，不仅加工制造难度大、生产成本高、不易于控制，并且由于体积大造成安装困难。因此，本文旨在设计一种结构简单、方便加工、成本低、体积小且易于控制的共振型UEVC装置。

为此，采用单激励的方式，设计一种新型阶梯变幅杆，得到简单结构的共振型超声椭圆振动超精密刀架，并对该装置进行动力学分析，确定结构参数，对装置前端质点的轨迹点进行拟合，得到椭圆振动轨迹，验证了设计的合理性。

1 结构设计与分析

图1所示为共振型超声椭圆振动超精密刀架，由新型组合梁阶梯型变幅杆和超声振动换能器(包括前盖板、压电陶瓷、后盖板和预紧螺栓)组成。超声换能器起到能量转换的作用，其输入端的信号频率为系统的固有频率。换能器在特定频率电压信号的激励下产生振动，使得变幅杆在其固有频率下发生振动，形成共振。图2为新型组合梁阶梯变幅杆，其右段为圆柱段，左段是直梁和两非对称斜梁构成的组合梁段，直梁和斜梁的横截面为矩形，组合梁和圆柱段均采用过渡圆弧联接。

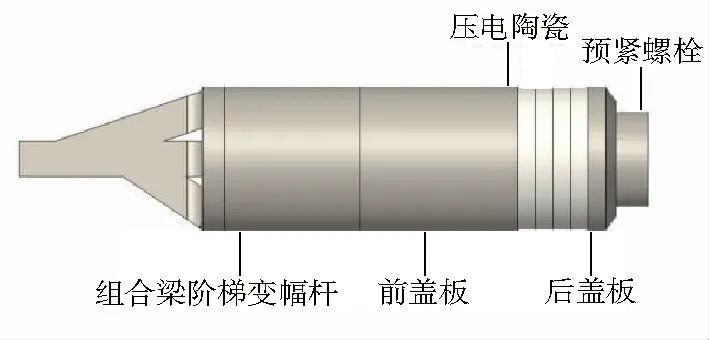
图1 共振型超声椭圆振动超精密刀架

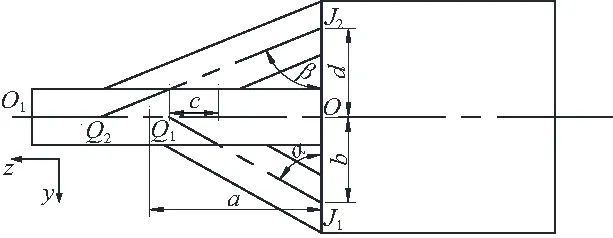
图2 组合梁阶梯变幅杆

若对超声振动换能器输入正弦电压信号，则换能器产生简谐振动并将振动传递到组合梁阶梯变幅杆，振动能量经过圆柱段后分别从组合梁底部的O、J1、J2处沿着直梁和两非对称斜梁继续向左传递，在Q2处交汇后继续传递到O1处。由于振动能量在直梁和两非对称斜梁之间传递的速度、距离以及振动形式的不同，振动能量沿两非对称斜梁分别传递到Q1处和Q2处后产生弯曲振动波和纵向振动波，继而在O1处会产生具有一定相位差的y向弯曲振动分量和z向纵向振动分量，两振动分量复合后生成了椭圆振动轨迹。

装置机构的初始尺寸由标准的郎之万方程获得，方程如式(1)所示。式(1)-式(3)中的符号描述如下：f为共振型超声椭圆振动超精密刀架的预期固有频率；c为固体材料中的声速，可由式(3)中弹性模量与质量密度之比的平方根估算出来；L1为组合梁阶梯变幅杆中直梁的长度尺寸；L2为组合梁阶梯变幅杆中圆柱段的长度；L3为前盖板的长度；L4为4片压电陶瓷的厚度；L5为后盖板的长度；ρ为材料的质量密度；A为横截面积。

(1)

(2)

(3)

2 建立有限元模型

2.1 建立几何模型

本文压电陶瓷的材料选用PZT-8，外径为40.25 mm，内径为20 mm，厚度为5 mm，选取数量为4片。由于电极片厚度极小，所以建模时选择将其忽略，根据图1所示共振型超声椭圆振动超精密刀架结构可知L4=20 mm。已知L4尺寸，采用半波长设计方案，根据式(1)-式(3)求得超精密刀架的初始结构尺寸：L1=L2=45 mm，L3=45 mm，L5=6 mm。初步设定组合梁阶梯变幅杆参数：a=38 mm，b=d=13 mm，c=20 mm。根据已获得尺寸参数建立超精密刀架的几何模型。为避免实际工作时超精密刀架由于应力过大出现断裂情况，组合梁与圆柱体的连接处采用过渡圆弧连接以降低应力值。

2.2 材料定义及网格划分

完成几何建模之后，定义共振型超声椭圆振动超精密刀架的材料属性。其中，新型组合梁阶梯变幅杆和前盖板材料为2Al2，压电陶瓷材料为PZT-8，后盖板和预紧螺栓材料为45钢，表1所示为各材料参数。由于在超精密刀架中存在电场和力场的耦合，所以压电体的网格单元选择压电耦合单元，压电陶瓷采用solid226单元，其他材料均采用默认单元。以约束法兰圆周面为边界条件，对模型整体进行网格划分，网格划分采用自适应网格划分技术，考虑到结果的收敛和计算效率问题，网格质量设置为中，单元尺寸设置为2.5 mm，获得的总节点和总单元数分别为632 005和20 284，有限元模型如图3所示。

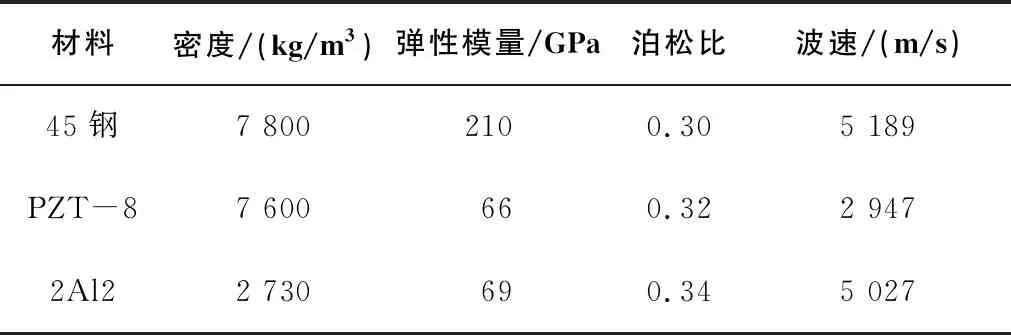
表1 共振型超声椭圆振动超精密刀架材料参数

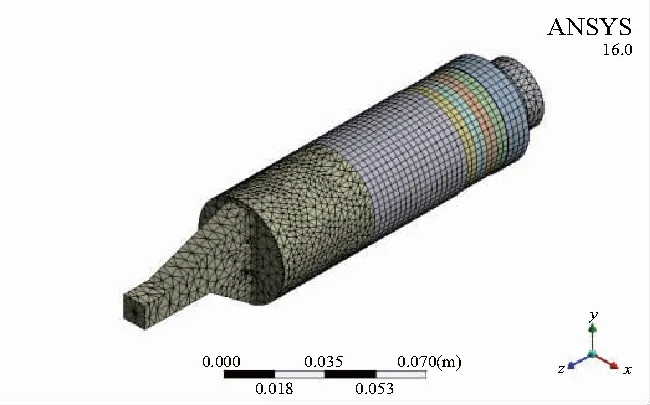
图3 共振型超声椭圆振动超精密刀架有限元模型

3 动力学仿真分析

3.1 模态分析

为了确定共振型超声椭圆振动超精密刀架的固有频率与振动模态，对装置模型进行模态分析试验。忽略螺栓预紧力的影响，组件之间接触类型设置为Bonded，边界条件设置为法兰圆周面固定，求解方法为block lanczos，求解范围为25 kHz～32 kHz。根据求解结果调整几何模型尺寸，当L1=52 mm，L5=15 mm时，结果较为满意。此时，得到共振型超声椭圆振动超精密刀架的振动模态云图(图4)和位移矢量图(图5)。结果显示超精密刀架的固有频率为28.68 kHz，且变幅杆输出端存在纵向和弯曲耦合振动。以超精密刀架的轴线方向为分析路径，得到装置的总变形图(图6)、振幅曲线图(图7)和应力曲线图(图8)(本刊黑白印刷，相关疑问请咨询作者)。结果显示超精密刀架的最大变形发生在变幅杆部分，最大振幅在变幅杆的输出端，最大应力发生在超精密刀架的装夹处和压电陶瓷处。

图4 振动模态云图

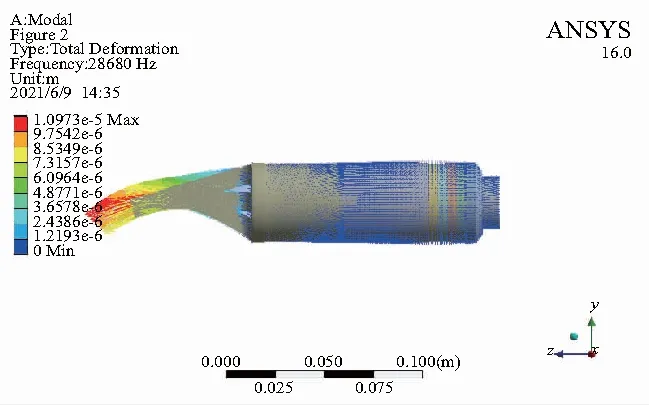
图5 位移矢量图

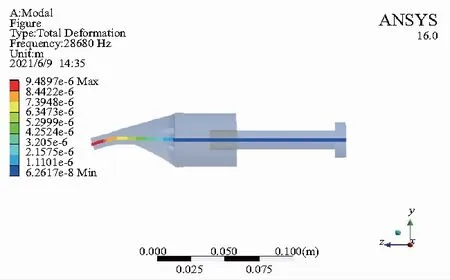
图6 装置轴线方向的总变形位移图

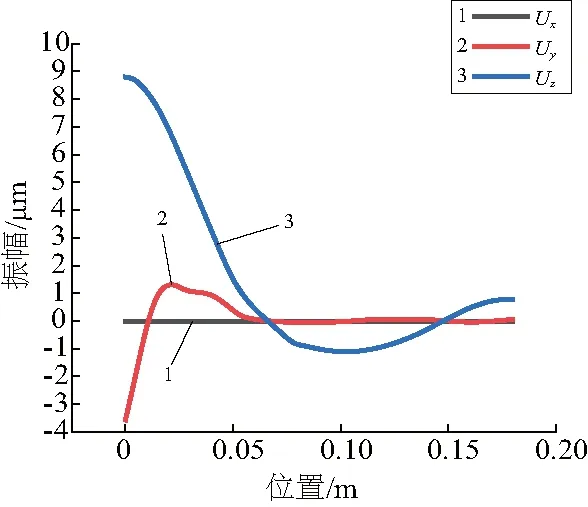
图7 装置轴线方向振幅曲线图

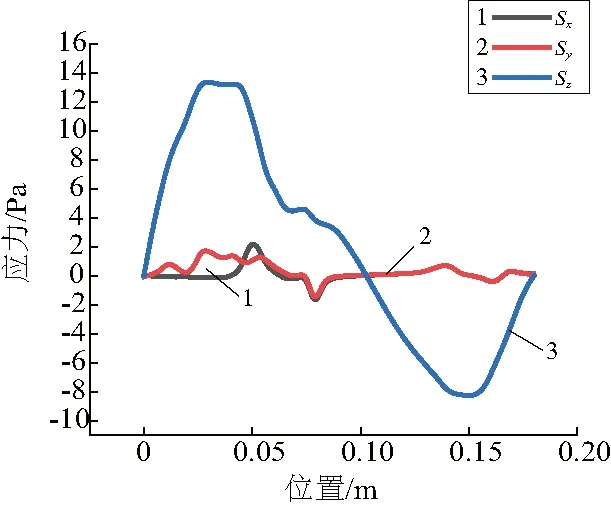
图8 装置轴线方向应力曲线图

3.2 谐响应分析

谐波响应分析用来确定共振型超声椭圆振动超精密刀架在已知频率和幅值简谐载荷作用下的稳态响应。根据共振型超声椭圆振动超精密刀架的有限元模型进行谐响应分析，求解方法采用模态叠加法，因此进行谐响应分析前首先要进行模态分析，并且模态分析的最高阶振动模态的频率不能低于谐响应分析的频率范围最大值的1.5倍。对于每个压电陶瓷给出幅值为1 N的输入力，在25 kHz～30 kHz频率范围内进行扫频分析，得到共振型超声椭圆振动超精密刀架前端质点的频幅响应曲线(图9)。在图9中，黑色、红色、蓝色曲线分别表示x方向的弯曲振幅、y方向的弯曲振幅、z方向的纵向振幅。在28.7 kHz附近共振型超声椭圆振动超精密刀架前端质点的y方向弯曲振幅和z方向纵向振幅均达到了最大值，即超精密刀架的共振频率和固有频率几近相同，且x方向弯曲振幅几乎为0。这表明法兰对于装置的振动基本没有影响，进而表明此装置的结构设计具有一定的合理性。

3.3 瞬态分析

瞬态动力学分析共振型超声椭圆振动超精密刀架结构在时变载荷作用下，结构质点的位移响应特征，用来预测超精密刀架前端质点的运动情况。根据共振型超声椭圆振动超精密刀架的有限元模型进行瞬态分析，插入压电模块，定义超精密刀架中压电陶瓷片的上下两面为电极面，且定义相邻两片的压电陶瓷上下面为压电耦合面，在压电陶瓷片的电极面上施加频率为28.68 kHz、幅值为100的正弦电压，求解载荷步设置为10个，步长时间为一个振动周期，每个载荷步的时间设置为振动周期的1/20，采用完全法进行求解。求解得到共振型超声椭圆振动超精密刀架前端质点处的运动轨迹曲线(图10)。在图10中可以看出，共振型超声椭圆振动超精密刀架前端质点的振动轨迹是椭圆轨迹，z向纵向振幅与y向弯曲振幅的比值约为2.5∶1。瞬态分析的结果表明共振型超声椭圆振动超精密刀架可以实现超声椭圆运动，证明此设计合理可行。

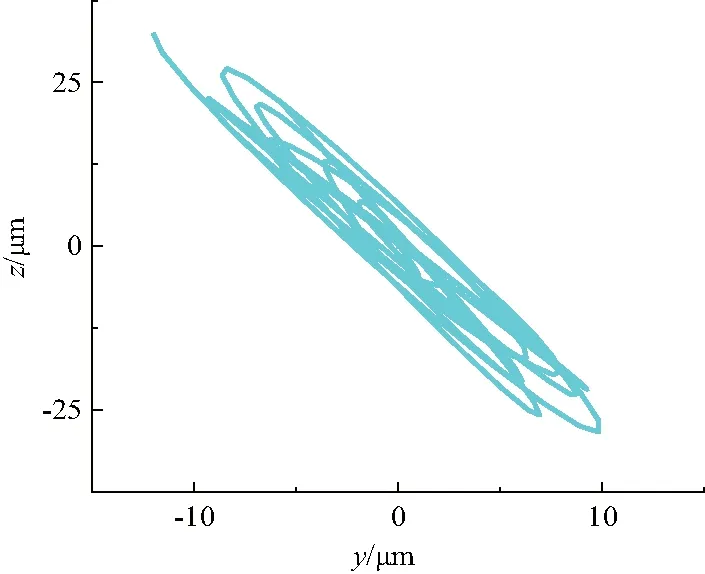
图10 刀架前端质点的振动轨迹

4 结语

本文提出了一种新型组合梁阶梯变幅杆的设计方法，研制出一种单激励的共振型超声椭圆振动超精密刀架，建立了超精密刀架的有限元模型并进行了动力学仿真分析，包括模态分析试验、谐响应分析试验以及瞬态动力学分析试验。动力学分析的结果表明共振型超声椭圆振动超精密刀架前端质点的振动为椭圆振动，验证了所设计的共振型超声椭圆振动超精密刀架的合理性。