近水平露天煤矿相邻采坑临时中间桥对边坡的支挡效应
2022-10-23梁祖超李广贺李雪健周志伟
王 东,梁祖超,李广贺,李雪健,周志伟
(1.辽宁工程技术大学 矿业学院,辽宁 阜新 123000;2. 神华宝日希勒能源有限公司,内蒙古 呼伦贝尔 021008)
露天矿在采用分坑开采时,必然会在相邻露天采坑形成中间桥,对于提高边坡稳定性与缩短运距发挥了重要作用。但在中间桥拆除过程中,对边坡的支挡效应必然逐步减弱,若处治不当易引发大规模滑坡,严重威胁矿山安全高效生产。如白音华二号露天煤矿、宝日希勒露天煤矿、胜利东二号露天煤矿等在中间桥拆除过程中,均曾发生过巨型滑坡;相反,吉林郭勒二号露天煤矿、胜利西三号露天煤矿、霍林河南、北露天煤矿、扎哈淖尔露天煤矿等均采用双坑基建或多坑并行开采方式,在中间桥拆除前,均未形成大规模滑坡。工程实践表明,相邻露天采坑中间桥能够提高边坡稳定性,客观认识并充分利用中间桥对边坡的支挡效应至关重要。
相邻露天采坑中间桥与边坡体组合而成的地质体具有特殊的空间形态和结构,以及显著的三维效应。目前,边坡稳定性分析仍广泛采用二维极限平衡法,已有的三维极限平衡法仅限于规则滑坡体的稳定性求解,对于相邻露天采坑中间桥支挡效应下的非规则边坡稳定性无法获得定量认识;数值模拟方法发展迅速,但对于复杂问题的求解仍缺乏可靠性。关于中间桥空间位置、形态及尺寸参数设计方面的研究仅限于从采矿工程角度出发,且仅顾及了技术与经济指标,忽略了中间桥及其动态拆除过程中对边坡稳定性的影响。因此,定量表征相邻采坑中间桥对边坡的支挡效应,提出科学有效的边坡稳定性计算方法,揭示中间桥几何形态参数对边坡稳定性的影响,是我国煤炭露天开采领域亟待解决的重要科学问题。
笔者在构建边坡与中间桥三维力学模型的基础上,基于摩尔-库伦抗剪强度理论,分区推导了中间桥三维支挡效应的数学表达式,提出了中间桥三维支挡效应的二维等效方法,揭示了中间桥空间形态参数对支挡效应及边坡稳定性的影响规律,以期为协同优化边坡与中间桥的形态参数提供科学手段。
1 中间桥对边坡的支挡效应分析
1.1 力学模型的建立
受矿山采运设备规格与剥采工程需求影响,中间桥的空间形态可近似为斜棱柱,从力学角度可视为具有特殊形态、力学属性分布不均匀的边坡支挡结构(图1(a))。通过力学分析,中间桥后方受非工作帮推力、自身的重力及底界面的支撑力和抗滑力的作用(图1(b))。显然支挡效应的大小由底界面抗滑力决定,基于抗剪强度的表达式可知,底界面抗滑力由中间桥的空间形态与底板岩层性质决定。对于特定的矿山,中间桥及其底板岩层性质均可视为已知量,此时,中间桥的支挡效应仅与其空间形态参数,,,有关。其中为中间桥底角,(°);,,,分别为中间桥的底宽、桥高、桥长与采坑总长度,m。
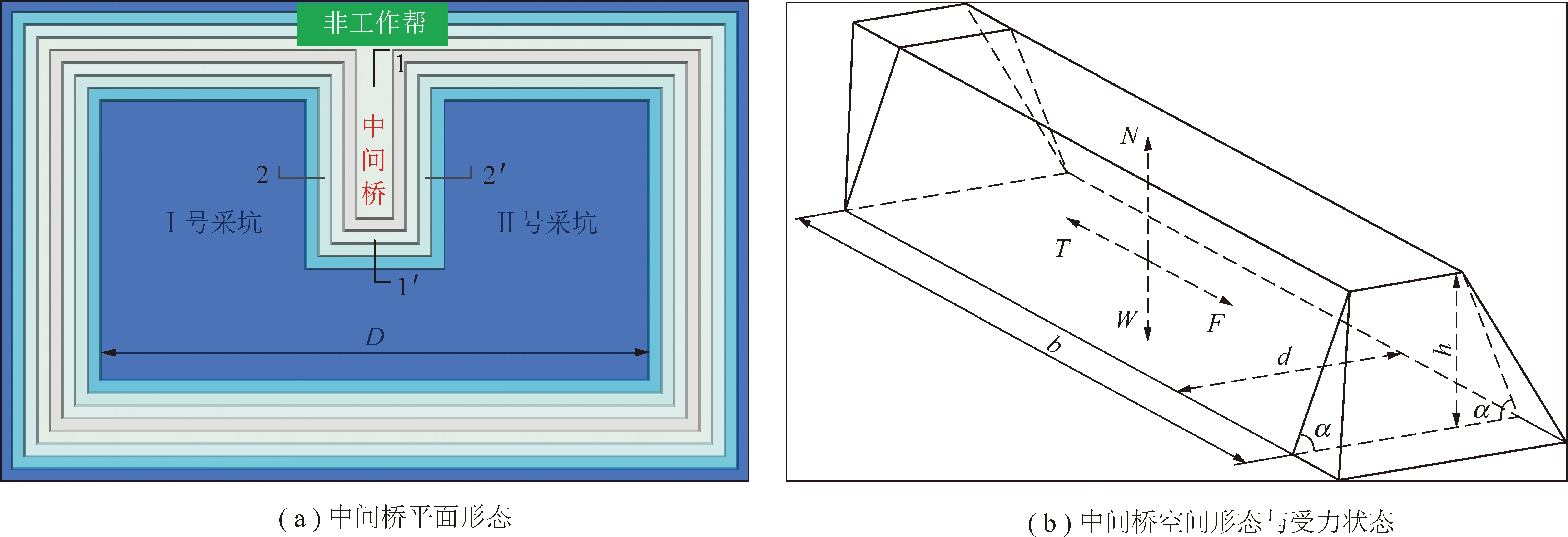
图1 中间桥平面形态与受力分析模型
1.2 中间桥的三维支挡效应解析
沿着中间桥倾向(1—1′)及走向(2—2′)方向切割剖面,断面形态如图2所示。中间桥的支挡效应仅与空间形态参数相关,根据其空间几何形态,将中间桥划分成3个区域,如图3所示。为方便计算,将中间桥多台阶边坡角用底角表示。区域Ⅰ的中间桥由2个锥体和1个柱体组成,体积为;区域Ⅱ的中间桥是以梯形为截面的柱体,体积为;区域Ⅲ的中间桥由2个锥体和1个柱体组成,体积为,分别表示为

图2 水平基底条件下中间桥断面形态计算示意
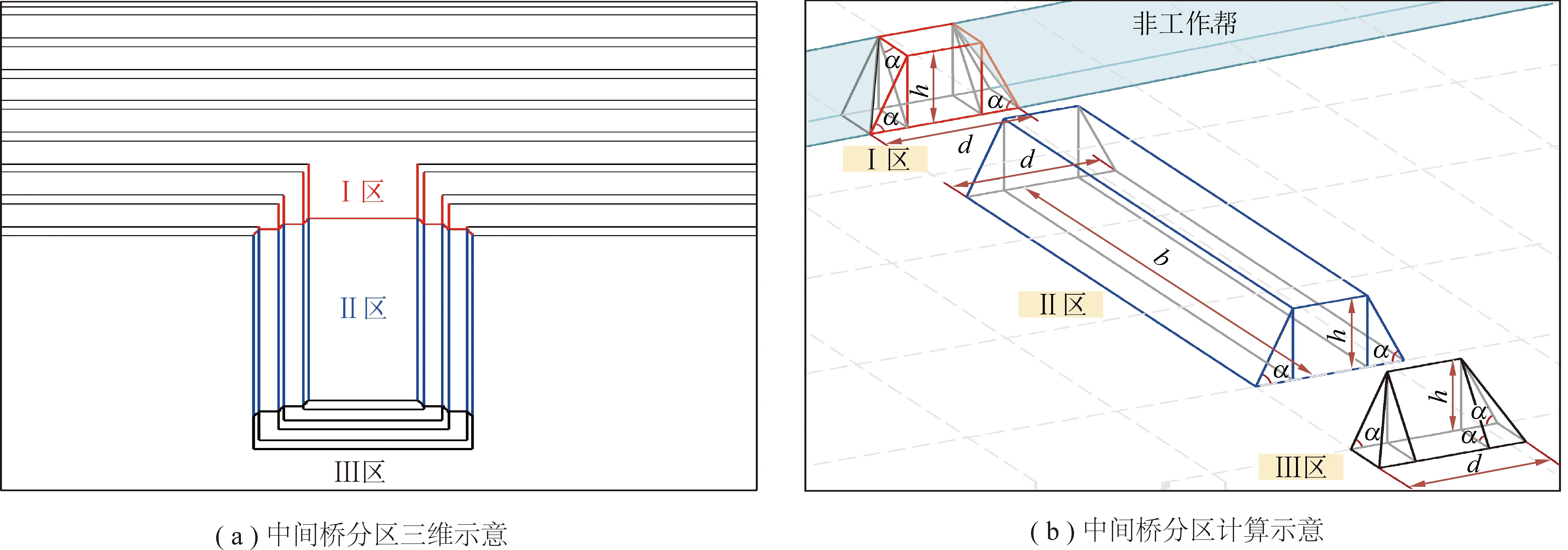
图3 中间桥分区示意
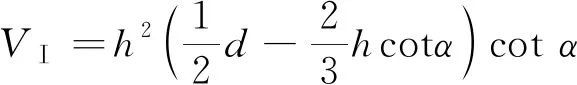
(1)
=(-cot)
(2)
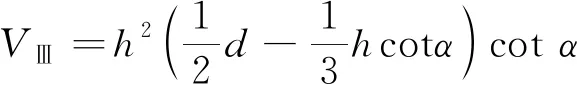
(3)
根据摩尔-库伦强度准则,即可获得Ⅰ,Ⅱ,Ⅲ区的抗滑力,,:
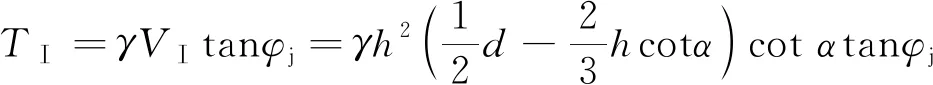
(4)
式中,为中间桥各岩层的加权容重,kN/m;为中间桥底板岩层的内摩擦角,(°)。
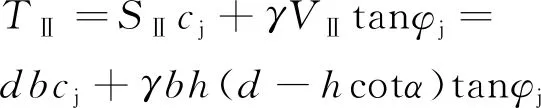
(5)
式中,为中间桥底板岩层的黏聚力,kPa;为中间桥Ⅱ区的底界面面积,m。
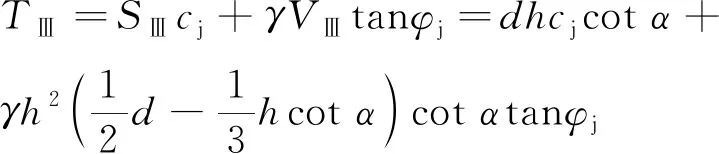
(6)
式中,为中间桥Ⅲ区的底界面面积,m。
将各区域抗滑力累加,中间桥提供的抗滑力为
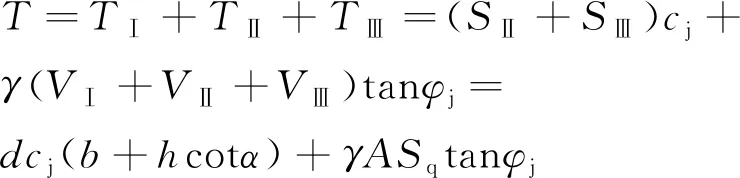
(7)
其中,=-cot;为中间桥沿倾向方向断面面积(图2),m。中间桥提供的抗滑力即中间桥对边坡的三维支挡效应。分析式(7)可知,中间桥的三维支挡效应与底界面面积、断面面积、桥体体积均呈正相关一次函数关系。
2 中间桥三维支挡效应二维等效方法
目前,二维刚体极限平衡法是边坡稳定性分析中最有效、应用最广泛的方法,为此,结合中间桥与边坡同步失稳的空间形态特征,从中间桥三维支挡效应实质出发,应用合并同类项方式,提出中间桥三维支挡效应的二维等效方法,是实现工程应用的关键。显然,中间桥的支挡效应为底界面的抗滑力,而采用二维刚体极限平衡法时,支挡效应是由贯通整个采坑底界面的抗滑力来提供,因此,只要找到合适的方法将中间桥底界面的抗滑力等效成贯通整个采坑底界面的抗滑力,即可实现三维支挡效应的二维等效。
分析式(4)~(6)可知,中间桥的三维支挡效应实质是一剪切反力,分别由抗剪强度参数黏聚力与等效摩擦因数tan提供。前者仅与中间桥的形态参数有关,后者则可能受中间桥煤岩分布影响,这与二维刚体极限平衡法中条块底界面抗滑力的组成类型与影响因素是一致的。因此,通过合并各区域抗滑力与对应等效抗滑力数学表达式的同类项可以求出各区域的等效黏聚力、等效内摩擦角或等效摩擦因数tan。需要注意的是,区域Ⅰ的中间桥为下部非工作帮边坡的上方压覆桥体,因此该区黏聚力不需要等效,只需要等效摩擦因数。压覆于非工作帮上方的区域Ⅰ中间桥相当于增加了底界面的摩擦力,所以在确定tan时应考虑该效应所带来的叠加。
令中间桥Ⅰ区支挡效应二维等效后的底界面抗滑力为,则
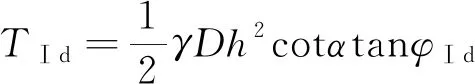
(8)
式中,为Ⅰ区等效内摩擦角,(°),Ⅱ区、Ⅲ区与Ⅰ区表示类似。
又=,根据式(4),(8)合并同类项可得
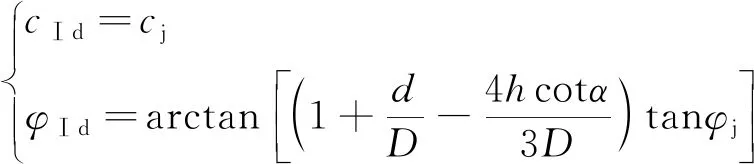
(9)
式中,为Ⅰ区等效黏聚力,kPa,Ⅱ区、Ⅲ区与Ⅰ区表示类似。
令中间桥Ⅱ区支挡效应二维等效后的底界面抗滑力为,则
=+tan
(10)
又=,根据式(5),(10)合并同类项可得
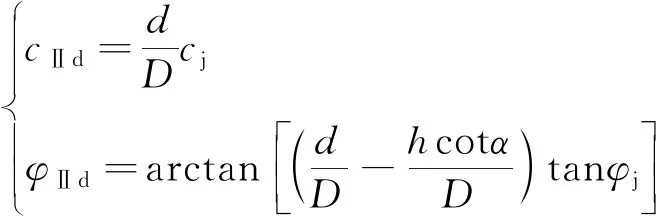
(11)
令中间桥Ⅲ区支挡效应二维等效后的底界面抗滑力为,则

(12)
又=,根据式(6),(12)合并同类项可得
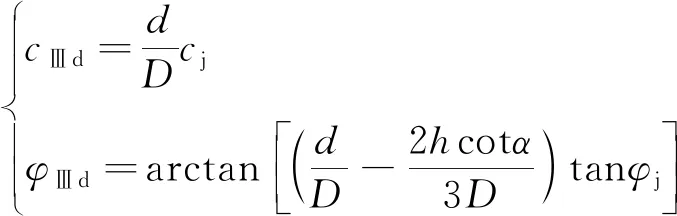
(13)
分析式(9),(11),(13)可知,中间桥Ⅰ区的等效黏聚力即底界面的黏聚力,等效摩擦因数tan与中间桥底宽呈正相关一次函数关系,与桥高、底角的余切值呈负相关一次函数关系;Ⅱ区和Ⅲ区的等效黏聚力及等效摩擦因数tan与中间桥底宽呈正相关一次函数关系,且等效黏聚力仅与底宽有关,等效摩擦因数tan与桥高、底角的余切关系同Ⅰ区一致;当底宽=0时,则桥高=0,中间桥对边坡无支挡效应;当=时,中间桥对边坡的支挡效应可近似表现为二维。考虑到边界条件影响,中间桥底宽∈(2cot,),桥高∈(0,tan/2)。
在我国边坡稳定性分析中比较常用的方法为剩余推力法,将上述二维等效后的抗剪强度参数引入到剩余推力法中,可建立中间桥支挡效应下边坡稳定性二维计算方法。
3 工程示例
3.1 工程背景
宝日希勒露天煤矿采场正常作业参数为平盘宽度40 m、坡面角70°、台阶高度一般为10 m和15 m。东帮岩层产状近似水平,自上至下主要由第四系和煤系地层组成。从岩体结构上看,第四系主要由砂土和黏土构成,属散体状岩体结构;煤系地层主要由煤层、泥岩构成,属层状岩体结构。露天矿由中间桥分为南北2个采坑,北部采坑深约210 m,开采至3煤;南部采坑深约120 m,开采至1煤。为实现矿山安全开采、经济效益最大化,探讨出中间桥形态参数与边坡稳定系数之间的关系是实现该目标的关键。剥采工程现状平面图和中间桥典型工程地质剖面如图4,5所示,岩土体物理力学指标见表1。

图4 宝日希勒露天煤矿剥采工程平面示意

图5 中间桥典型工程地质剖面
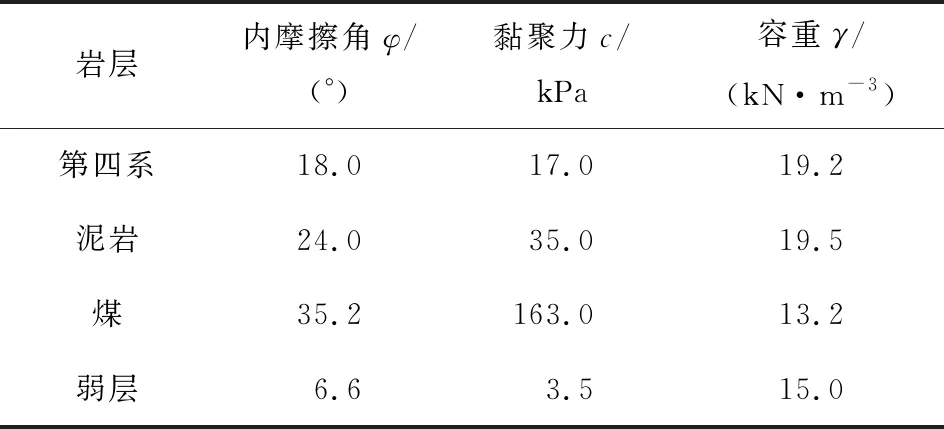
表1 岩土体物理力学指标
3.2 中间桥支挡效应影响因素分析
式(9),(11),(13)表明中间桥底宽、桥高以及底角均是影响中间桥支挡效应的因素,笔者基于Origin软件,采用控制变量法对单一因素进行研究,揭示中间桥形态参数对支挡效应的影响规律,分析结果如图6~8所示。
从图6~8可以看出,工程实例揭示的中间桥形态参数对支挡效应的影响规律与理论分析具有一致性;Ⅰ区计算中,等效黏聚力即中间桥底板岩层黏聚力的力学参数,等效摩擦因数tan与中间桥底宽呈正相关一次函数关系,与桥高呈负相关一次函数关系,与底角呈正相关;Ⅱ区和Ⅲ区计算中,等效黏聚力与中间桥底宽呈正相关一次函数关系,探讨桥高及底角影响时,由于控制底宽不变,等效黏聚力与桥高、底角呈常函数关系,等效摩擦因数tan与中间桥底宽、桥高、底角的函数关系同Ⅰ区一致。中间桥底宽对等效黏聚力影响幅度较大,对等效摩擦因数tan次之。
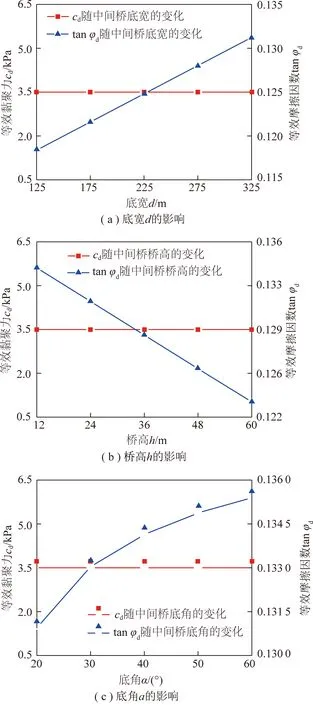
图6 Ⅰ区中间桥支挡效应与形态参数的关系曲线
3.3 中间桥形态参数对边坡稳定性影响分析
为探讨出更符合规律性的中间桥形态参数与稳定系数之间的关系,笔者借鉴宝日希勒露天煤矿工程实例,采用工程示例进行说明。结合剥采工程现状,工程示例在底角=18°,20°,22°三种工况下,采用控制变量法(底宽=500 m,桥高=70 m,桥长=300 m,采坑总长=1 800 m),对不同底宽、桥高、桥长与边坡稳定系数之间的关系进行探讨。对于任意给定的底宽、桥高、桥长,通过式(9),(11),(13)可获得不同底宽、桥高、桥长所对应的各区域等效黏聚力及等效摩擦因数tan,从而可利用边坡稳定性二维分析确定稳定系数(分别列举底角=20°的工况下不同中间桥形态参数对应的边坡稳定性二维分析结果,如图9所示),分析可得出边坡稳定系数与中间桥底宽、桥高、桥长的关系曲线如图10所示。不同底宽、桥高、桥长所对应的沿边坡走向方向的截面面积及压帮量见表2。需要注意的是,为控制计算时划分的条块数量一致,采用固定滑面进行计算。

图7 Ⅱ区中间桥支挡效应与形态参数的关系曲线
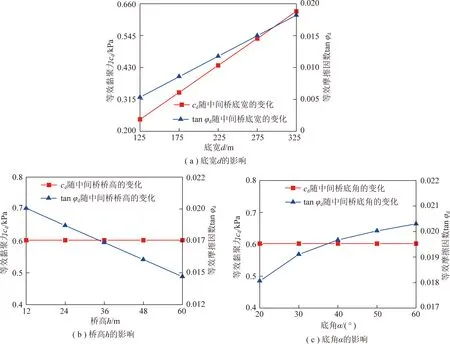
图8 Ⅲ区中间桥支挡效应与形态参数的关系曲线
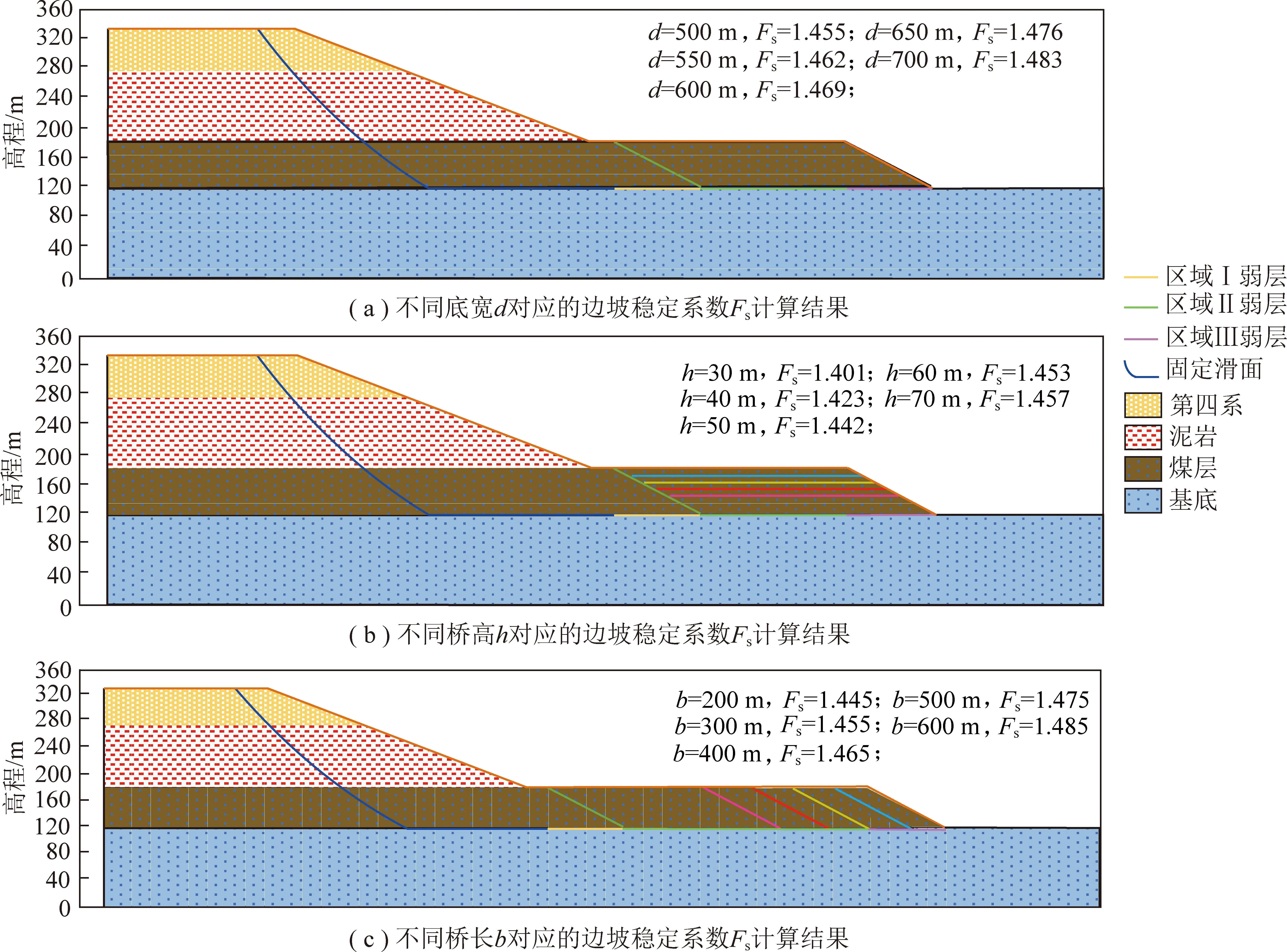
图9 α=20°时不同中间桥形态参数对应的边坡稳定性二维分析结果
由表2可知,中间桥截面面积及压帮量随底宽、桥高、底角和桥长增大而增大,且增大的幅度有所不同。对于截面面积,增大幅度的顺序为>;对于压帮量,增大幅度的顺序为>>。结合中间桥底宽对支挡效应的影响规律可判断:不同底宽对应边坡稳定系数的上升幅度应大于不同桥长对应边坡稳定系数的上升幅度。
分析图10可知,边坡稳定系数与底宽、桥长呈正相关一次函数关系,且与表2分析具有一致性;边坡稳定系数随桥高、底角增大而增大,上升梯度逐渐减小。
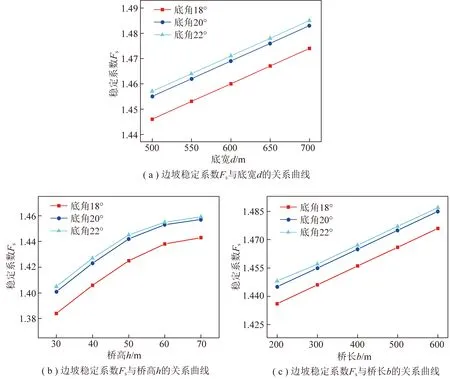
图10 边坡稳定系数Fs与中间桥形态参数的关系曲线

表2 中间桥截面面积及压帮量计算
4 结 论
(1)将中间桥视为在底界面剪切力作用下的边坡支挡结构,基于摩尔-库伦准则,推导了中间桥三维支挡效应的数学表达式,实现了中间桥对边坡三维支挡效应的定量表征,表明该效应的大小与中间桥的空间形态密切相关,分析得出中间桥的三维支挡效应与底界面面积、断面面积、桥体体积均呈正相关一次函数关系。
(2)从中间桥三维支挡效应产生的实质出发,应用合并同类项方式,提出了中间桥三维支挡效应的二维等效方法,完成了中间桥底界面等效黏聚力与等效内摩擦角的定量表征,实现了三维力学问题向平面应变问题的转化,可与经典的剩余推力法相结合,对边坡稳定性计算问题进行求解。
(3) 依据中间桥与边坡的相对位置以及自身的空间形态,将中间桥沿边坡倾向划分为3个区域。Ⅰ区等效黏聚力即为中间桥底界面的黏聚力,Ⅱ区和Ⅲ区等效黏聚力与中间桥底宽呈正相关一次函数关系;各区域等效摩擦因数tan均与中间桥底宽呈正相关一次函数关系,与桥高、底角的余切值呈负相关一次函数关系。因此,增大底宽、底角有利于提高其支挡效应。
(4)工程示例表明,在中间桥支挡作用下,边坡稳定系数随中间桥的桥高、底角增大而增大,上升梯度逐渐减小,且与底宽、桥长呈正相关一次函数关系。
