基于相干函数和仿生小波变换的双麦克风语音增强算法*

卞金洪高尚尚刘海波周 锋王如刚

(盐城工学院信息工程学院，江苏 盐城 224051)

在嘈杂的环境中，音频设备的效果较差。为了提高数字音频的质量和清晰度，近年来研究者提出了多种语音增强算法。其中单通道降噪技术，由于其实现简单，在过去的50 年里得到了广泛的应用[1-2]。许多单麦克风语音增强方法被提出，如谱减法[3]、卡尔曼滤波[4-5]和维纳滤波[6-7]。然而，由于噪声估计存在一定的困难，当语音受到非平稳噪声破坏时，这些单通道语音增强算法的性能就会下降。双麦克风降噪算法在提升语音质量和可理解性方面表现较好，为抑制语音中的平稳或非平稳噪声提供了一种解决方案。此外，与麦克风阵列语音增强技术相比，双通道语音增强算法易于实现，计算复杂度更低。

目前已经有多种较为流行的双麦克风降噪算法。在参考文献[8]中，作者提出了一种利用复谱平面的双麦克风语音增强方法，该方法适用于免提通信系统，比原来的复谱圆质心方法效果更好。Koulal 等人[9]提出了一种基于互功率谱密度的双通道语音增强算法，该方法采用改进的最小跟踪(IMT)技术进行噪声功率谱密度的估计。在参考文献[10]中，作者描述了两种基于谱减法的双麦克风降噪算法，这两种算法利用了两路信号的功率谱密度和互功率谱密度。此外，在文献[11]中提出了一种改进的基于相干函数的算法。该方法适用于两个排列紧凑的麦克风，不需要估计噪声统计特征值。此外，Kim 等在文献[12]中提出了一种基于双麦克风差分的噪声方差估计来进行降噪，该方法利用了信噪比估计，并在不同的噪声条件下证明了其有效性。最后，Nabi 等人[20]中提出了一种利用卡尔曼滤波的双麦克风降噪算法，该算法利用了相干函数和卡尔曼滤波器。

结合前面引用的工作，本文提出了一种基于相干函数的双通道降噪算法。该方法对于两个距离很近的麦克风，仍有较强的降噪能力，并且不需要像文献[12]中提出的算法那样进行噪声统计估计。此外，为了提高语音质量，本文提出了基于相干算法和仿生小波变换相结合的算法。本文的组织结构如下，第1 节给出了原始相干函数和估计相干函数。第2 节描述了我们所提出的使用卡尔曼滤波的仿生小波算法和所提出的双通道语音增强方法。第3 节介绍了在语音质量感知评价(Perceptual Evaluation of Speech Quality，PESQ)、时域波形和谱图分析方面，与其他方法相比，本文所提出方法的性能有所提升。最后，对本文进行了总结。

1 相干函数理论

本节介绍两个输入信号的相干函数。假设两个麦克风放置在噪声源和语音源互相分离的噪声环境中。延时补偿后，两个输入信号表示如下:

式中:s1(m)和s2(m)分别表示第一个和第二个麦克风的语音信号，类似的，n1(m)和n2(m)则表示噪声信号。上述两个信号的傅里叶变换可以表示为:

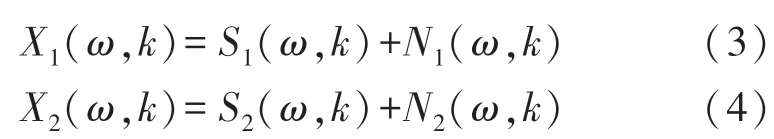
式中:k表示帧序号，ω表示频率。ω=2πd/L，L为帧长。相干函数是通过使用两个麦克风来估计语音信号的一种准则[13-14]。上述两个信号之间的相干函数的计算公式为:

Px1x2表示两路信号的互功率谱，Px1和Px2分别表示信号的自功率谱。

相干函数的大小用于收集有关噪声或语音存在的信息。因此，当幅值趋近于零时，语音占主导地位，当幅值趋近于一时，噪声占主导地位。本文使用了两个紧密间隔的麦克风的配置。因此，干扰信号是高度相关的，特别是低频[22]。在这种情况下，当噪声扩散时，相干函数为实值，可解析表示为:

图1 麦克风位置布局图

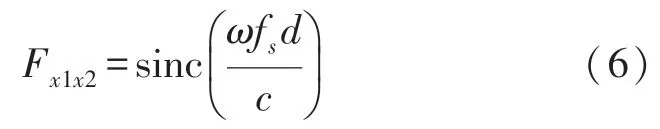
根据图中的设计，相干函数可以表示为:

式中:d为第一个麦克风与第二个麦克风之间的间距，c为声速，fs为采样频率，文中设置为16 kHz，α为入射角。相干函数一般可以用语音信号和噪声信号和的形式来表示，所以可以定义为:

式中:Ps1、Ps2、Pn1、Pn2分别表示语音源s1和s2的自功率谱，噪声源n1和n2的功率谱。

两路麦克风信号的信噪比(SNR)可以表示如下:

因此，文献[11]中定义的估计相干函数可以表示为:

式中:τ=fs(d/c)=SNR1=SNR2，这是因为两个麦克风距离很近时，信噪比的值几乎相同。

2 基于仿生小波变换和卡尔曼滤波的降噪算法

仿生小波变换(Bionic Wavelet Transform，BWT)是一种融合了主动耳蜗[23]机制的小波变换。此外，仿生小波变换描述了一个良好的能量规范，在其系数中表现出良好的语音分离性能。该算法应用于语音增强领域[15-16]，优于其他单麦克风降噪算法，如:Ephrahim 和Malih 滤波器[17]，谱相减[3]和离散小波变换[18]。

由于卡尔曼滤波器能对系统状态[4]进行最优估计，所以其成为了解决随机系统中线性MMSE 问题的常用滤波器。如图2 所示，本问题所提出的降噪算法使用了卡尔曼滤波器，如文献[19]所示，该降噪算法是受到维纳滤波器在仿生小波变换中应用降噪的启发。从图2 中可以看出，卡尔曼滤波器是应用于仿生小波变换系数对噪声信号的应用。然后，利用仿生小波变换的逆变换得到增强信号。

图2 基于仿生小波变换的卡尔曼滤波降噪算法

图2 中k1，k2，…，k18是输入信号的18 个仿生小波系数是经过卡尔曼滤波后得到的18个增强信号的仿生小波系数。

本文提出的双麦克风降噪算法分为两步。首先是文献[11]中提出的基于相干函数的双通道语音增强方法。在这一步中，通过在x2(m)上应用了双麦克风降噪系统均使用过的延迟补偿。然后，在每帧内用汉宁窗对两个噪声信号进行处理，并对每个信号进行75%的重叠和快速傅立叶变换(FFT)。接下来，计算公式(10)中定义的估计相干函数，从而计算最终的降噪增G(ω，k)。最后通过IFFT 和拼接叠加算法来得到时域增强信号。

第二步是基于小波变换和卡尔曼滤波的降噪算法。将该算法添加到基于相干的方法中，可以提高已经增强的语音信号的语音质量。图3 展示了本文提出的降噪算法的原理框图，图中的仿生小波变换卡尔曼滤波即为图2 中的原理。

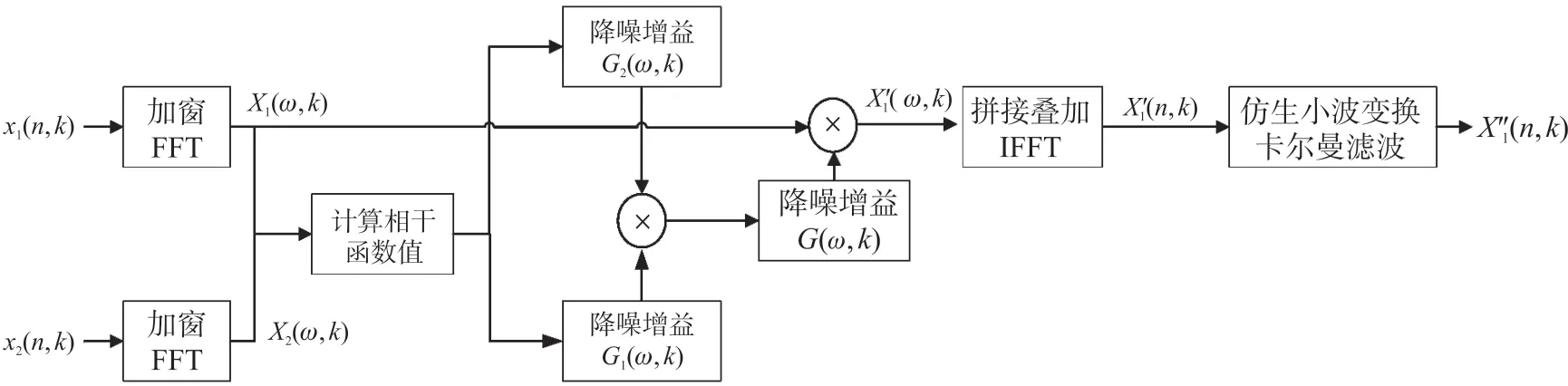
图3 双麦克分语音增强算法原理框图

3 实验与分析

本节将对提出的算法与其他双麦克风语音增强算法进行比较。使用语音质量感知评估(Perceptual Evaluation of Speech Quality，PESQ)分数来评估语音的客观质量。PESQ 分数范围为-0.5 到4.5[21]，分数越高语音的可懂度和质量越好。同时，使用了语谱图和时域波形对信号进行评估。语谱图分析能较好地反映残余噪声结构和降噪算法产生的语音失真，在信噪比为5 dB 的情况下，两个麦克风距离为2 cm 时，对所提算法进行了MATLAB 代码测试。通过在clean HINT 数据集中添加不同噪音类型来模仿真实的噪声环境，语音数据的采样频率为16 kHz，帧长为20 ms，帧叠75%，FFT 使用的窗函数为汉宁窗，将本文所提出方法的增强语音信号与基于相干函数的方法[11]以及基于相干函数和卡尔曼滤波算法[20]增强的语音信号进行了比较。

图4 为在单个135°的噪声源干扰情况对语音进行降噪时，不同方法下增强信号的PESQ 评分。实验结果表明，该算法在该种噪声场景下的PESQ评分都取得了较好的结果。此外，该算法相较对比方法的PESQ 分数平均提高了0.2。

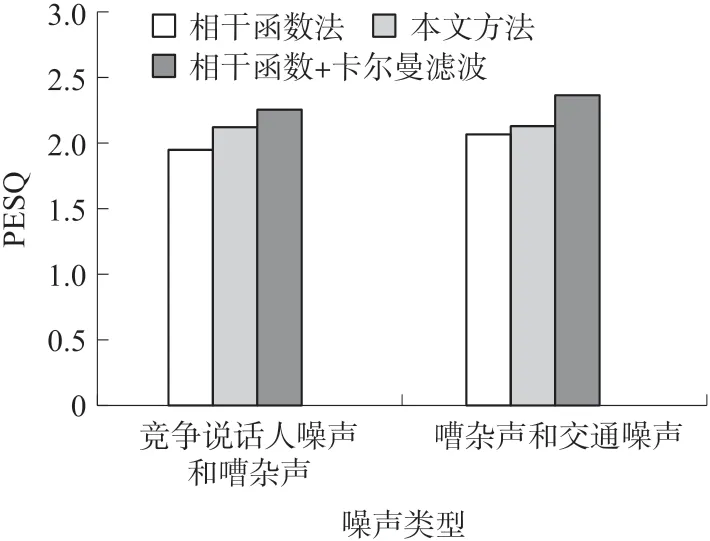
图4 单个噪声源(135°方向，信噪比为0 dB)下增强语音的PESQ 结果对比

图5 为两个置于90°和180°的噪声源对语音干扰的情况下，进行降噪时多种方法的增强信号的PESQ 评分。可以明显看出，该算法在该种噪声环境下的性能优于其他算法。此外，本文提出的的算法相较于对比方法，PESQ 评分提高了0.3 以上。

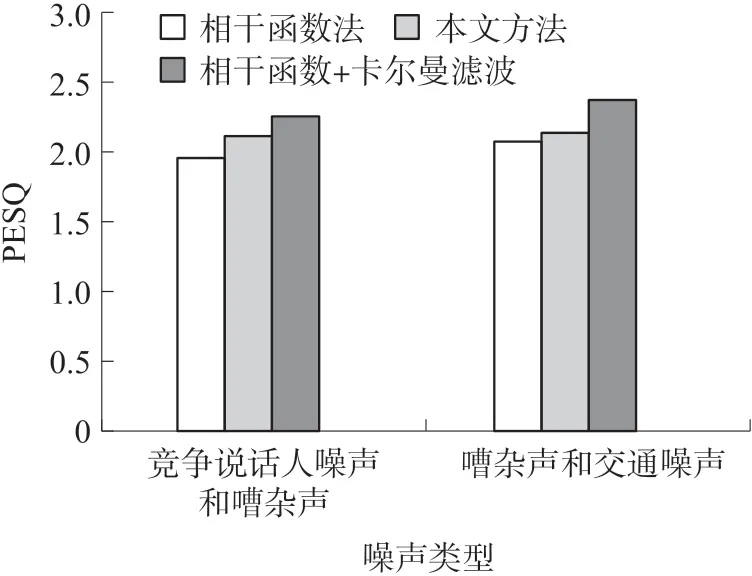
图5 两个单噪声源(90°和180°方向，信噪比为0 dB)下增强语音的PESQ 结果对比

噪声信号和其他增强信号的时域波形如图6 所示，在信噪比为5 dB 时，语音被噪声削弱，本文所提出的方法相较基于相干函数和卡尔曼滤波的方法抑制残留噪声的效果更好。

图6 纯净语音、带噪语音和不同方法的增强语音时域波形对比图

图7 展示了在信噪比为5 dB 时，纯净信号、带噪信号以及增强信号的语谱图。实验结果表明，该方法比基于相干函数和卡尔曼滤波的方法能更有效地降低残余噪声，且语音失真程度较弱，特别是语音的一些低频区域。基于以上对不同信号的语谱图分析和PESQ 评分所得的结果基本一致，证明了本文所提出算法的优越性。

图7 纯净语音、带噪语音和不同方法的增强语音语谱图

4 结束语

本文介绍了一种基于相干函数和仿生小波变换的双麦克风语音增强算法。通过对输入信号应用仿生小波变换得到仿生小波系数，然后采用Kalman 滤波，得到增强后的仿生小波系数。该算法可以在不同的噪声环境下利用两个排列紧凑的麦克风来处理噪声信号。该方法在PESQ 评分、时域波形和频谱分析等方面取得了良好的效果。本文提出的方法性能良好，运算复杂度较低，易于实现，可用于移动的低功耗音频设备。